基于皮爾遜理論與徑向基函數神經網絡的光伏功率預測

李光華

（中移（杭州）信息技術有限公司）

0 引言

大規模光伏并網發電在解決能源問題上有著重要作用［1］，但光伏輸出受太陽輻射強度、溫度等各種因素影響，導致其輸出具有時變性，給并網的控制調度帶來較大的挑戰。因此對功率的準確預測，可以有效提高電力系統并網運行的安全性和穩定性［2－3］。

目前光伏預測主要采用物理建模法和數學統計法對未來的光伏功率進行預測。物理建模法通過天氣預報獲取太陽輻照強度、太陽輻照時間以及云量等氣象因素，結合光伏板實際的工作特性獲得光伏輸出數據［4］。數學統計法對歷史數據進行分析，可以更好地映射輸出功率與歷史數據的關系。尤其隨著現代化光伏電站的建設，歷史發電及氣象數據更多維，統計預測方式發展更迅速［5－8］。

文獻［5］將太陽輻照作為輸入建立線性回歸算法，僅用太陽輻照強度一個輸入量對光伏功率進行預測，使得預測精度不高。文獻［6］用濕度和氣溫作為輸入，采用自組織特征對天氣類型進行聚類，分季節建立基于BPNN網絡的短期功率預測，但只以兩個參數作為輸入，容易陷入局部最優問題。文獻［7］以太陽輻照強度、溫濕度、風速等作為預測輸入，采用BPNN進行建模。該方案預測結果有一定提升，但是BPNN易陷入局部最小化誤區。文獻［8］采用相鄰日的歷史數據，用Elman神經網絡進行建模。該方案在氣象條件變化不大時預測精度較高。

本文提出以皮爾遜相關系數確定對光伏輸出影響較大的氣象因素，以最佳相似日和待預測日的氣象因素作為輸入，構建徑向基函數神經網絡對功率進行預測。RBF結構簡單，學習收斂速度快，具有很強的逼近非線性函數能力。

1 皮爾遜相關系數法確定輸入參數

本文的歷史數據有：輸出功率、風速、氣溫、相對濕度、水平面總輻照度、水平面散射輻照度。其中某些維度對輸出影響較大，對這些因素進行關聯度的分析，從而確定預測參數［10－11］。

本文用皮爾遜相關系數法，篩選出與光伏功率相關性較大的氣象因子。0.8～1.0表示極強相關，0.6～0.8表示強相關，0.4～0.6表示中等程度相關，0.2～0.4表示弱相關，0.0～0.2表示極弱或無相關。式中，ρX，Y表示皮爾遜相關系數，X、Y分別氣象因素和功率，N為樣本數量。

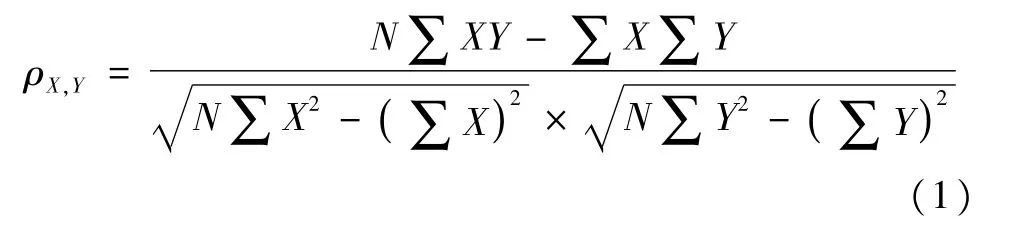
為直觀顯示光伏輸出功率與各氣象因素的關系，圖1以某日從8：00到18：00，展示輸出功率與各氣象因素的關系：為定性計算功率與各氣象因素的相關性，本文采用皮爾遜相關系數法計算相關度。其計算結果如表1所示。為兼顧輸入維度以及計算速度，本文選擇相關度較高的前3個氣象因素作為預測的輸入。

圖1 光伏功率與各氣象因素關系圖

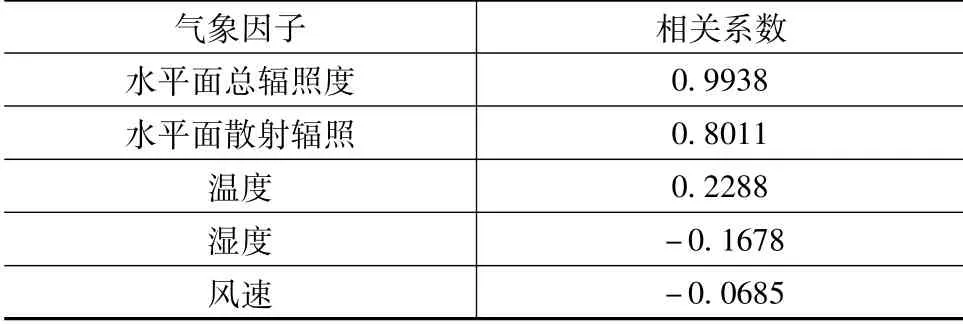
表1 光伏功率與各氣象因素的相關系數

2 相似日的選擇

光伏系統輸出功率受天氣等自然條件的影響，在類似的氣象條件下，光伏輸出功率類似［12］。為提高光伏發電功率的預測精度，需從大量的歷史數據中，篩選出與待預測日氣象條件相似度較高的相似日作為預測的輸入變量。每個輸入向量可用如下表示：

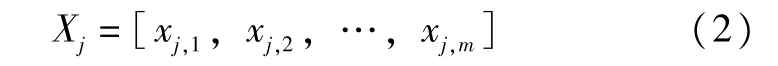
式中，Xj表示第j日的輸入向量；xj，m表示第j日第m維輸入數據。

由于各氣象因素的量綱不同，并且數值范圍也差多個數量級，便于后續數據的處理，需要對各個維度的輸入數據進行歸一化處理。歸一化公式如下：

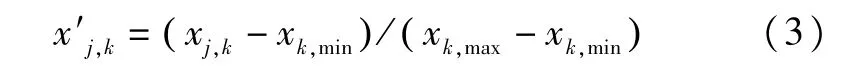
待預測日的氣象數據可從氣象部門獲取，采用歐式距離法計算最佳相似日：

式中，Dj表示第j日與待預測日的歐式距離；表示第j日的第k維輸入數據；x′k表示待預測日的第k維輸入數據；m為輸入向量的維數。

3 徑向基神經網絡

徑向基函數神經網絡是前向神經網絡，于1988年提出，根據生物神經元具有局部相應的特點，將RBF引入神經網絡中。RBFNN具有三層結構。第一層為輸入層，由信號源節點組成。第二層為隱藏層，串聯輸入層和輸出層，其變換函數是徑向基函數，是對中心點徑向對稱且衰減的非負局部響應函數。第三層為輸出層，用于對輸入完成輸出的變換，本文為輸出的功率值。輸出層是對線性權值進行調整，采用的是線性優化策略，因而學習速度較快［13］。

由于被控對象具有非線性、多變量特性，考慮到RBF能任意逼近非線性函數，在網絡結構簡單的條件下，有很好的泛化能力，因此本文選擇用RBF作為預測模型，對光伏功率的輸出進行預測。

4 實驗數據及結果分析

本文的輸入向量由最佳相似日的功率、水平面總輻照度、水平面散射輻照、日最高溫度、日最低溫度以及待預測日的日最高溫度、日最低溫度組成。輸出向量由待預測日的輸出功率組成。以某光伏發電站的公開數據，作為本次的實驗數據進行預測模型的訓練。

為考察訓練獲取的模型的預測能力，將其與BPNN進行比較。本文從每個季節中隨機選擇一日進行預測，其預測結果與實測功率見圖2。

圖2 功率預測與實測值關系圖

為定量考察模型的預測能力，本文采用均方根誤差eRMSE和平均絕對百分比誤差eMAPE對預測結果進行分析，其計算方式如下：

式中，P′i為預測值；Pi為實測值；N為采集數目。

兩種預測模型得到的誤差值如表2所示，可以看出，使用RBFNN的相似日模型相較于BPNN，其eRMSE的BPNN均值從7.93降低到RBFNN的5.04，其eMAPE的BPNN的均值從18.26%降低到RBFNN的7.05%。

表2 預測誤差比較

5 結束語

本文采用皮爾遜相關系數法，選擇對輸出功率影響較大的氣象因素作為輸入參數。再以這些輸入參數，根據歐氏距離選擇待預測日的最佳相似日，用RBF神經網絡建模進行功率的預測，結果表明采用該方案的預測模型預測性能較佳，具有一定的實用價值。