高電壓增益阻抗源逆變器的小信號模型分析

程諄

湖南鐵道職業技術學院，湖南 株洲 412001

0 引言

新能源發電技術已成為抑制環境污染和能源危機的有效途徑[1-4]。并網逆變器作為新能源發電并網的核心部件近年來發展迅猛[5-8]。

2002年彭方正教授提出了一種Z源逆變器拓撲結構，解決了傳統逆變器中的諸多問題，為國內外學者提供了一種全新的思路[9]。近年來，為了進一步提高阻抗源逆變器的升壓能力，降低其開關應力，國內學者不斷探索，對阻抗源逆變器拓撲結構進行了研究，主要通過在阻抗源網絡中引入變壓器、耦合電感、開關電感來提升這方面的性能[10-16]。文獻[10]提出的改進型Z源逆變器，將三相逆變橋與阻抗源網絡位置顛倒，在一定程度上抑制了啟動時存在的電流過沖，它與Z源逆變器相比，在相同的直流鏈電壓下其電容電壓應力更小，但升壓能力不足。文獻[11]提出的準Z源逆變器，在相同的升壓比下其電容電壓應力降低，并且通過合理調節電感L1的位置，使得輸入電流連續，但其升壓能力仍然受到調制因子的制約。文獻[12-13]提出的T型Z源逆變器，引入了漏感很小的變壓器代替Z源逆變器中的兩個電感，并減少一個電容，進而通過改變變壓器變比和直通占空比來靈活調節輸出電壓。相較于Z源逆變器，在相同的直通占空比和調制因數下，T型Z源逆變器可以通過調節變壓器變比提高輸出電壓從而提高其升壓能力，并且減少了無源器件的個數，使得逆變器尺寸減小、成本損耗降低。但是隨著變壓器變比的增大其漏感也會增大，反而會導致變壓器直流側鏈電壓降低，從而使得升壓效果受到抑制。文獻[14]提出的開關耦合電感Z源逆變器，用含有耦合電感的無源網絡替代其中一個電感。當耦合系數k接近于1時，可調節耦合電感的匝比和直通占空比來獲得更大的電壓增益。但是耦合電感會帶來漏感，在非導通模式下，會產生電壓尖峰縮短橋臂上器件的使用壽命；而且，雖然其升壓能力會隨著匝數比的增大而增大，但是過大的匝數比會導致變壓器體積增大使得銅損增加效率降低。文獻[15]提出的開關電感Z源逆變器，相較于Z源逆變器，雖說多了6個二極管和2個電感使得成本增加，但是只需要極短的直通狀態即可獲得較高的升壓比，從而避免了升壓比和調制因數的矛盾關系，使得升壓能力得到了顯著提升。但由于電容電壓初始值為零，開啟時會產生很大的浪涌電流；并且其仍然存在Z源逆變器輸入電流不連續等問題。文獻[16]提出的一種開關電感準Z源逆變器，將準Z源逆變器中的一個電感替換為一個開關電感支路，使得其具備開關電感Z源逆變器升壓能力強的優勢，并且保留了準Z源逆變器輸入電流連續的優點。文獻[17]提出的一種高電壓增益阻抗源逆變器，它較傳統Z源逆變器具有更高的電壓增益和更低的電流諧波。

本文針對高電壓增益阻抗源逆變器進行研究。首先從直通和非直通狀態入手，分析其穩態工作原理；然后推出升壓因子和直通占空比的表達式。并且運用狀態空間平均法建立狀態空間方程，引入小擾動建立其小信號方程，通過對波特圖和零極點軌跡的分析得出阻抗源網絡電容電感值大小對于系統穩態性能和動態性能的影響，可為系統參數設計提供理論指導。

1 拓撲結構及穩態工作原理

高電壓增益阻抗源逆變器的拓撲結構如圖1所示，分別討論直通情況與非直通情況，并進行分析。

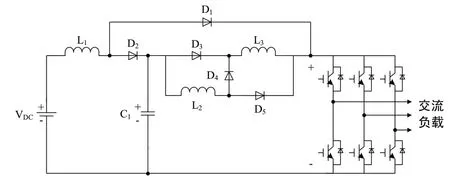
圖1 高電壓增益阻抗源逆變器拓撲結構

當網絡處于非直通狀態時，二極管導通情況如圖2所示。

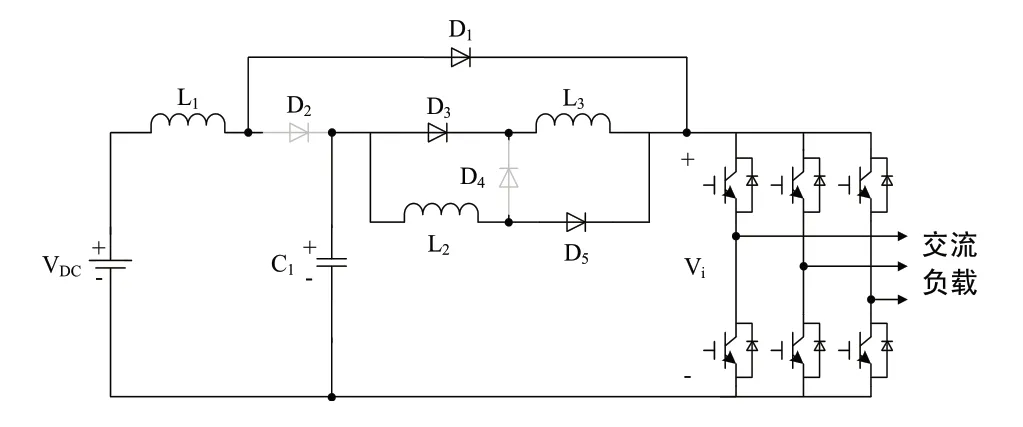
圖2 直通時系統的等效電路

可得如下式（1），并且其中Vi=0：

當網絡處于非直通狀態時，二極管導通情況與直通時相反，如圖3所示。

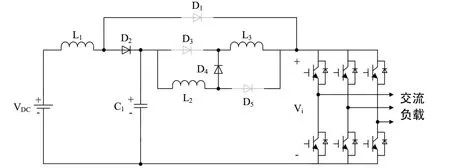
圖3 非直通時系統的等效電路

可知：

式（2）和式（3）中：VL1、VL2、VL3分別表示電感L1、L2、L3兩端的電壓；VC1表示電容C1的電壓；iC1表示電容C1的電流；iL1、iL2、iL3分別表示電感L1、L2、L3兩端的電流；VDC表示直流電源電壓；Vi表示高電壓增益阻抗源網絡的輸出直流電壓。

在一個開關周期T中，直通時間為T0，非直通時間為T1，直通占空比為d0=T0/T。高電壓增益阻抗源逆變器網絡電感L1的端電壓平均值VL1、高電壓增益阻抗源逆變器網絡電感L2的端電壓平均值VL2、高電壓增益阻抗源逆變器網絡電感L3的端電壓平均值VL3均為0，可知：

上式中：VL3NST、VL2NST分別表示非直通狀態時電感L1、L2兩端的電壓。

由式（3）可得：

可知，高電壓增益阻抗源網絡輸出電壓的平均值Viav可表示為：

2 小信號模型分析

假設系統工作在電流不斷續的狀態，并假設L1=L2=L3=L0定義四個狀態變量為：

那么將直通狀態下高電壓增益阻抗源逆變器的等效方程（1）轉化為的形式，可得：

其中：

同理，此式中矩陣系數對應的分別為：

由[（5）*d0+（6）*（1-d0）]，可以得到系統狀態方程：

使用狀態空間平均法對高電壓增益阻抗源逆變器進行建模，獲得大信號方程為：

使用狀態空間平均法，得到矩陣A為：

矩陣B為：

此處的d0為系統動態時的直通占空比。

同樣，利用狀態空間平均法，可得系統網絡的靜態工作點為：

其中：

上式中，D0為系統網絡穩態工作點的直通占空比。同理：

其中，IL1、IL2、IL3、VC1分別為靜態工作點的電感電流及電容電壓。

是靜態工作點的輸出電壓。

由式（9）可知，系統狀態為穩態時：

對平均模型中的狀態變量進行小信號擾動，建立小信號模型。將擾動小信號，依次帶入式（8）中，可得：

將其再代回（9）式，即可化簡為：

對上式進行拉式變化可得：

由上式可知系統輸入的擾動量就是：輸入的直流電壓擾動（也就是輸入電壓擾動），以及直通占空比的擾動。因此，只需將其中一個小信號擾動量設置為零，就可以得到另一個輸入狀態變量的小信號傳遞函數。

可知，直通占空比控制至電感電流iL1的傳遞函數為：

在上式中：

直通占空比控制至電容電壓vC1的傳遞函數是：

輸入電壓（直流側）至電容C1的傳遞函數為：

3 動態性能分析

通過式（24）和式（25），采用表1所示的系統參數，繪制出小信號傳遞函數GVd1（s）和Gid1（s）的零極點軌跡如下。

表1 高電壓增益阻抗源逆變器仿真參數

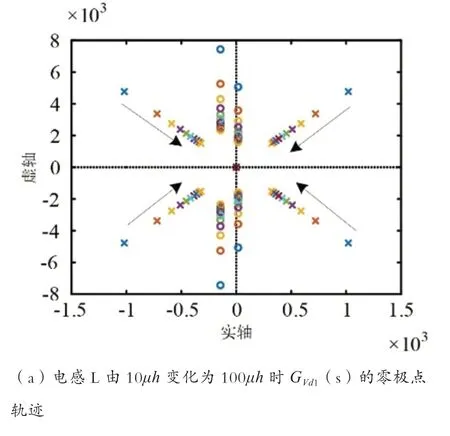
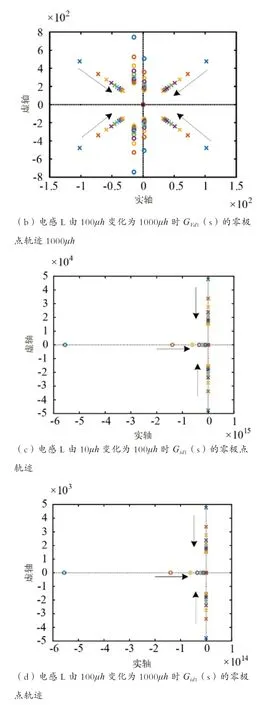
圖4 電感變化時的零極點軌跡

圖5 電容或直通占空比變化時的零極點軌跡

由圖分析可知，位于虛軸右側的零點不會因電容參數的變化而發生變化，但是當系統中電感值或者直通占空比增大時，右側的零點會移向虛軸。

4 結語

本文針對高電壓增益阻抗源逆變器，建立了其小信號模型，在此基礎上，得到了各個狀態變量的小信號傳遞函數，并依據小信號傳遞函數得到系統零極點模型。分析了高電壓增益阻抗源逆變器的動態性能與阻抗源網絡電感、電容參數以及直通占空比之間的關系。得出阻抗源網絡電感、電容值越大，系統動態響應越慢，因此在進行參數設計時要兼顧穩態、動態性能，電感、電容取值不應過大。