設定值濾波型四參數二自由度PID算法研究

殷華文

(南陽理工學院智能制造學院，河南 南陽 473004)

0 引言

在工業控制領域廣泛應用的回路比例積分微分(proportional integral derivative,PID)控制器和Smith預估控制器等常規控制器，都只能設定一組控制器參數，屬于一自由度控制器。一般而言，如果按干擾抑制特性最優來整定參數，則設定值跟隨特性差；如果按設定值跟隨特性最優來整定參數，則干擾抑制特性差。所以常規控制器的設計和參數整定通常采用折中或試湊的辦法解決[1]。這樣可以滿足大多數控制系統的要求。但對于高性能控制系統而言，該方法難以達到期望的控制性能。這時，就需要采用二自由度PID控制。

二自由度控制是指：采用適當的設計方法，找到兩組獨立的參數并設計出兩個獨立的控制器，分別用優化系統的設定值跟隨特性和干擾抑制特性[1]。二自由度PID的基本概念是由I.M.Horowitz在1963年提出的[2]。抑制外部干擾用微分先行PID控制算法，調節Kp、Ti與Td參數，可有效地改善系統動態響應，實現最優的干擾抑制特性。而對于設定值干擾，在PID算法之前疊加設定值濾波器以調節濾波器參數α，可減緩設定值的快速變化，從而實現最優的設定值跟隨特性。這就是四參數二自由度PID算法。

近年來，隨著各種新型先進控制技術的出現，為了更好地發揮二自由度控制的優勢，一些研究者已將新的控制思想與PID控制器或者控制結構相結合，提出了不同的二自由度控制器的設計方法。如：基于內模控制原理的二自由度控制、基于模糊控制理論的二自由度控制等[3]。雖然二自由度控制方法研究已取得較大進展，但大多僅限于利用仿真試驗進行理論驗證。因此，將理論研究成果推廣應用于實際工業過程還有待實現。

本文針對大小慣性不同的四種典型過程對象，進行二自由度控制算法研究。

1 二自由度PID算法設計

1.1 二自由度PID算法思想

二自由度PID算法是在微分先行PID算法的基礎上加上設定值濾波環節，實現設定值跟隨性和抗干擾性同時最優。

通常的PID算法是基于偏差補償原理的，即PID運算是基于偏差e的。偏差值為設定值和反饋值的差值，即：

e=r-y

(1)

式中：e為偏差；r為設定值；y為反饋值。

由式(1)可以看出，e受r和y雙因素變化的影響。PID控制器既要抑制r變化的影響，又要抑制y變化的影響。干擾d會直接影響到y的變化。r往往是階躍變化的。d是現場擾動信號，既可能是一種信號，也可能是幾種信號的混合。因此，用一組PID參數難以兼顧對設定值階躍的跟隨和抗干擾。為了抑制設定值階躍的影響，需要弱化微分作用；而為了捕捉干擾對被控變量的影響，又需要強化微分作用。為了抑制干擾，需要增強比例積分作用以消除余差。但增強比例作用會增強設定值階躍對控制系統的沖擊，而增強積分作用會引起積分飽和。設定值濾波型六參數二自由度PID控制結構如圖1所示。

圖1 設定值濾波型六參數二自由度PID控制結構圖

二自由度PID的算法思想就是對引起e變化的雙因素采用不同的策略分別進行抑制。圖1所示的設定值濾波型六參數二自由度PID控制結構需要六個參數，即設定值濾波器三個參數α、β、γ和三個PID參數[4]。

六參數二自由度PID算法結構比較復雜。圖2所示的是簡化的設定值濾波型四參數二自由度PID控制結構[5-6]。這種結構只對設定值作慣性濾波，只有一個二自由度系數α。

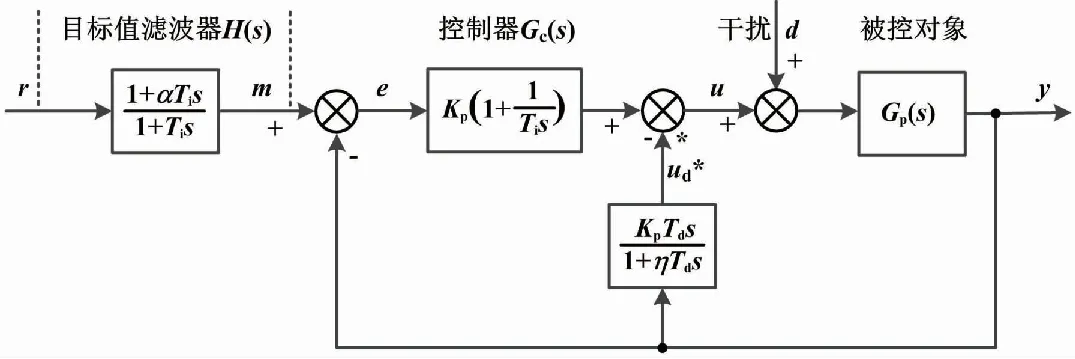
圖2 設定值濾波型四參數二自由度PID控制結構圖

1.2 濾波器提高系統的設定值跟隨能力

設定值濾波器用于緩沖設定值階躍對系統的沖擊、減輕控制器的工作壓力，即主要考慮式(1)中r因素對偏差e的影響。

設計目標值濾波器H(s)，如式(2)所示：

(2)

對式(2)作推導，得：

(3)

由式(3)可知，設定值濾波器實際是一個比例環節和慣性環節的迭加。當0<α<1時，比例環節對設定值階躍的初始值進行了衰減，慣性環節則緩沖了設定值階躍對系統的沖擊。濾波器可以使設定值階躍時被控變量有一個平穩的變化空間，從而更好地跟隨設定值變化，不影響系統的穩定性。

1.3 微分先行的干擾抑制能力

在控制系統的實際運行過程中，設定值是階躍變化的。這將使微分項輸出產生極大的突變(比例項輸出也會跳變，但沒有微分項跳變幅度大)。微分突變一方面會使控制變量產生很大的變化，對于有些生產過程(如化學反應、燃燒等過程)是不允許的；另一方面，還會使被控變量產生很大的超調。為了避免設定值變化引起的微分突變，本文提出了微分先行的概念。微分先行是指將控制器的微分部分前移至測量通道中[7]。

微分先行算法只對測量值作微分處理，而不影響比例積分(proportional integral,PI)的調節。微分先行PID的控制結構如圖1中去除目標值濾波器的部分。

微分先行可以減輕設定值階躍引起的微分突變。但是對于二自由度PID而言，加上設定值濾波器后減弱了設定值階躍時的微分跳變。這時的微分先行主要起抑制干擾的作用，即主要用來抑制y因素對偏差e的影響。這是由于微分先行是對被控變量y作微分，可以直接捕捉擾動d導致的被控變量y的變化，從而使控制系統能夠抑制干擾。

微分環節對廣義對象形成局部反饋，相當于對廣義對象引入反饋校正。反饋校正可以消除廣義對象非線性、變參數的影響和抑制干擾[8]。微分運算加了微分延遲，所以對干擾信號有濾波和緩沖作用。

1.4 微分先行運算的極性

對于一般的PID運算來說，微分部分的運算是：

(4)

式中:Kp為比例系數；Td為微分系數。

式(4)的離散化形式為：

(5)

式中：Ts為采樣周期;e(k)為當前采樣時刻偏差；e(k-1)為上一采樣時刻偏差。

微分運算捕捉的是偏差的變化，PID算法的輸出為：

u(k)=up(k)+ui(k)+ud(k)

(6)

式中：up(k)為比例運算項；ui(k)為積分運算項；ud(k)為微分運算項。

(7)

式中：y(t)為被控變量。

式(7)的離散化形式為：

(8)

式中：y(k)為當前時刻被控變量采樣值；y(k-1)為上一采樣時刻被控變量。

由式(8)可以看出，微分項運算已經不受設定值r的影響了。微分運算項只捕捉被控變量y的變化。

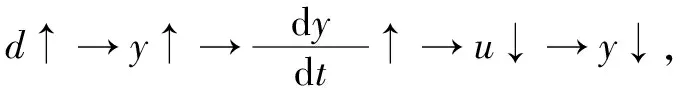
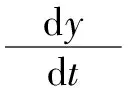
(9)

結合式(6)和式(9)，微分先行運算和正常的微分運算極性相反，所以圖1和圖2中標“*”處為“-”而不是“+”。

1.5 二自由度PID公式離散化

把系統分成兩個部分：①設定值濾波器部分；②標準PID加微分先行部分。

①把目標值濾波器H(s)看成一個簡單的控制系統，對式(2)作拉氏反變換，得：

(10)

離散化之后,得：

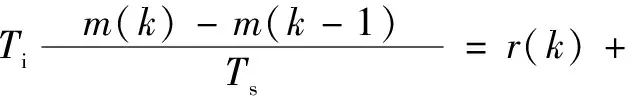
(11)

整理之后,得：

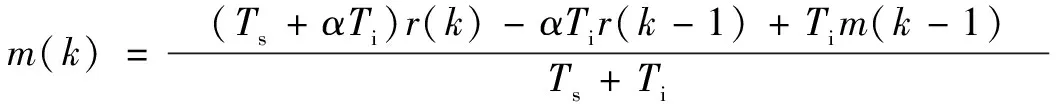
(12)

m(k)、y(k)分別是PID運算的輸入和被控變量，則：

e(k)=m(k)-y(k)

(13)

②將微分先行PID部分離散化，則整個控制算法為：

(14)

其中，微分項為：

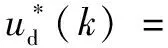
[y(k)-y(k-1)]

(15)

式中:η為微分延遲系數或不完全微分系數,是為了抑制微分突變而加的慣性延遲環節的時間常數Td的系數，η取值一般為0.1～0.2。

2 MATLAB/Simulink中的仿真研究

2.1 設定值濾波器研究

在MATLAB/Simulink中搭建設定值濾波器進行仿真:輸入信號r為階躍信號;α和Ti的取值用四組不同的參數。濾波器輸出信號曲線如圖3所示。

圖3 濾波器輸出信號曲線圖

由圖3可知，濾波器輸出信號曲線是疊加了α值的慣性環節單調上升曲線。

當0<α<1時，相當于把設定值階躍的初始值進行了縮小。但由于慣性環節的作用，濾波器信號輸出m最終都將上升到設定值r。α決定了濾波器信號輸出曲線的初始值，即設定值將被縮小的程度。而另一個參數Ti則決定了曲線上升速度的快慢。Ti越小則上升速度越快。由于慣性環節的相位滯后影響，濾波器輸出信號曲線相對于原始設定值曲線相位滯后0～90°。

2.2 一自由度PID算法和二自由度PID算法的比較研究

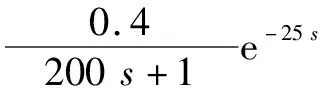
圖4 一自由度PID和二自由度PID控制仿真比較(α=0.35)

由圖4可知，一自由度PID控制有比較大的超調，二自由度PID控制既無超調也無振蕩，響應曲線能夠很好地跟蹤濾波器輸出信號曲線，體現了二自由度PID控制的優點。但一自由度PID控制響應速度快，而二自由度PID控制響應速度慢。

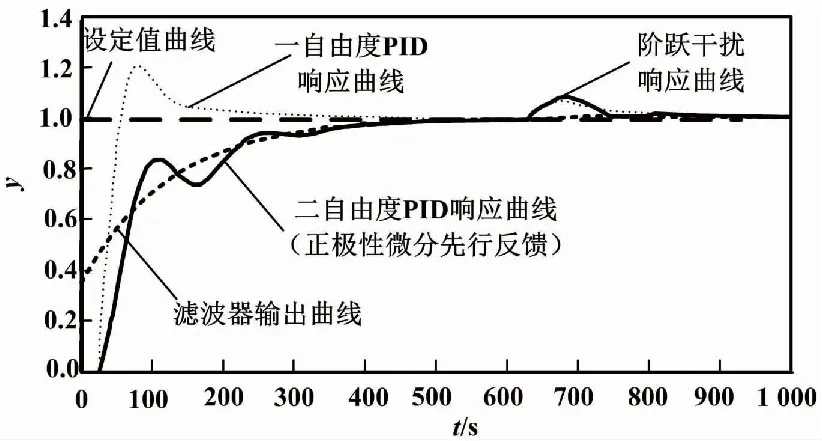
圖5 正極性微分運算控制仿真曲線(α=0.35)

3 大小慣性對象二自由度PID控制

3.1 試驗研究對象

本文對水泵壓力、管道流量、水箱液位、鍋爐溫度這四個慣性大小不同的對象進行二自由度PID算法控制效果研究。經過實際測試，這四個對象的數學模型如下。

3.2 水泵壓力二自由度PID控制

水泵壓力對象的慣性小，不容易穩定。通過響應曲線法和經驗試湊法，整定出調節效果較好的PID參數(即Kp=0.67、Ti=20 s、Td=1 s)，再整定α參數。水泵壓力一自由度PID算法和二自由度PID算法控制曲線如圖6所示，可見二自由度PID控制效果優于一自由度PID控制效果。

圖6 水泵壓力一自由度PID算法和二自由度PID算法控制曲線

通過改變出水口調節閥改變出水流量施加擾動，二自由度PID控制能抑制壓力的波動。

由于水泵壓力是小慣性對象，比例參數Kp和微分參數Td不要設置得過大，約1 s即可，否則系統會出現振蕩現象。設置α=0.01時，調節時間、最大偏差和穩態誤差都比較小。

3.3 管道流量二自由度PID控制

管道流量是典型的過程對象，具有慣性小、非線性的特點[9]，所以不容易穩定。通過響應曲線法和經驗試湊法，整定出調節效果較好的PID參數(即Kp=0.11、Ti=30 s、Td=0 s)，再整定α參數。α=0.1時，管道流量二自由度PID控制曲線如圖7所示。

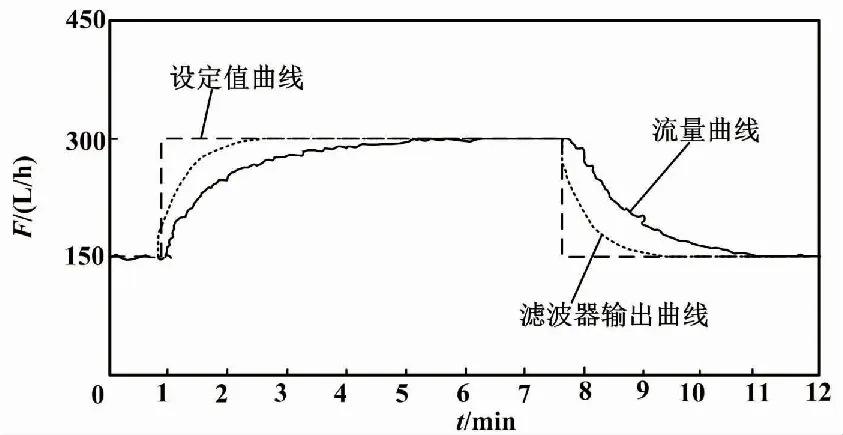
圖7 管道流量二自由度PID控制曲線(α=0.1)

由于管道流量是小慣性對象，比例參數Kp和微分參數Td不宜設置得過大，否則系統會出現振蕩現象。設置α=0.1時，調節時間、最大偏差和穩態誤差都比較小。

3.4 水箱液位二自由度PID控制

通過響應曲線法和經驗試湊法，整定出調節效果較好的PID參數(即Kp=3.45、Ti=200 s、Td=15 s)，再整定α參數。α=0.35時，水箱液位二自由度PID控制曲線如圖8所示。

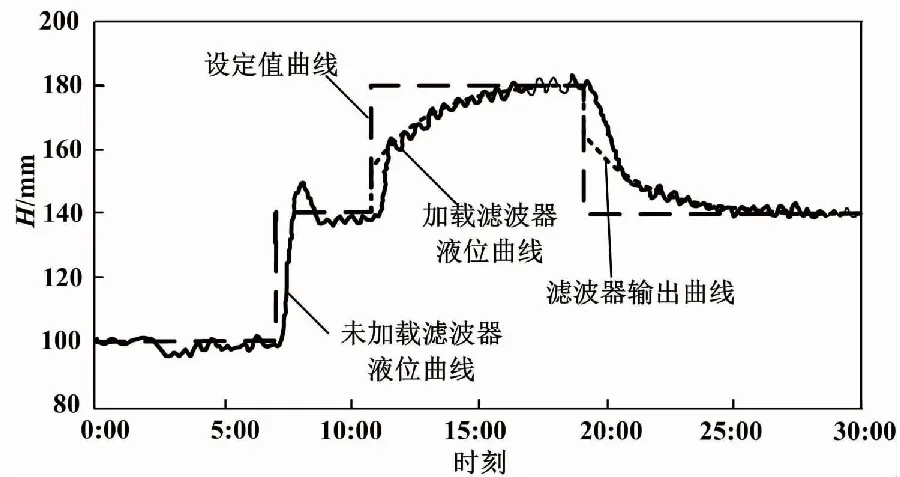
圖8 水箱液位二自由度PID控制曲線(α=0.35)

水箱液位是大慣性對象，比水泵壓力和管道流量對象的慣性大。如果沒有超調問題，而需要快速穩定，則需要增大比例參數Kp。但Kp過大時也會產生振蕩。α越大，設定值濾波后曲線的上升時間越短，但超調量也越大。

3.5 鍋爐溫度二自由度PID控制

鍋爐溫度是典型的過程對象，具有大慣性、大滯后和非線性等特點[10]。

此處鍋爐溫度為非自衡積分對象，加熱過程散熱較慢，具有較大的滯后。鍋爐溫度控制既要求快速升溫，又要避免超調，所以控制難度大。

本文先整定出PID參數(即Kp=20、Ti=50 s、Td=10 s)，再整定α參數。α=0.5時，鍋爐溫度二自由度PID控制曲線如圖9所示。

圖9 鍋爐溫度二自由度PID控制曲線(α=0.5)

由于鍋爐溫度控制有積分環節，即大慣性環節，為了提高執行器的能力，α取值應偏大。

3.6 二自由度PID的參數整定

二自由度PID的參數整定應先整定PID參數，通過響應曲線法、繼電反饋振蕩法和經驗試湊法等，整定出調節效果較好的PID參數。然后施加擾動，修正所得的PID參數，使調節器的抗干擾性最佳。四種對象的參數設置規律為：水泵壓力對象Kp=0.67,管道流量對象Kp=0.11,水箱液位對象Kp=3.45,鍋爐溫度對象Kp=20。由此可知，大慣性對象的Kp參數要大，而小慣性對象的Kp參數要小。

然后，根據對象慣性大小進行α參數整定，使設定值跟蹤特性最佳。四種對象的α參數設置規律為：管道壓力對象α=0.01，管道流量對象α=0.1，水箱液位對象α=0.35，鍋爐溫度對象α=0.5。由此可知，大慣性對象的α參數要大，而小慣性對象的α參數要小。

α參數一般不要超過0.5。若大于0.5，雖然有緩沖設定值的功能，但緩沖效果隨α的增大的變化并不明顯。當α=1時，無設定值緩沖效果。

4 結論

二自由度PID相當于兩個調節器的串聯。第一個調節器是設定值濾波器，實際是一個比例環節和慣性環節的迭加，相當于對設定值作了一次PI調節。第二個調節器是對系統偏差作了一次微分先行PID調節。兩個調節器共用一個積分參數Ti。

設定值濾波器對設定值階躍幅值的衰減降低了設定值階躍擾動對系統造成的沖擊，慣性環節的緩沖也減小了系統超調的可能性，比例和慣性環節的迭加使系統具有良好的跟隨性。微分先行是對測量值作微分，可以直接捕捉擾動導致的被控變量的變化，從而更好地實現控制系統的干擾抑制性。二自由度PID能實現設定值跟隨和擾動抑制的雙優控制。但由于設定值濾波器中慣性環節的相位滯后作用，設定值跟隨性是以犧牲響應速度為代價的。

在整定控制參數時，被控對象慣性大，則Kp和α參數設置要大，使得設定值濾波器和PID運算輸出增大。被控對象慣性小，則Kp和α參數設置要小，使得設定值濾波器和PID運算輸出減小。