核心素養下小學生數學思維品質的培養路徑

☉劉樹剛

數學學科核心素養體現在數學抽象、邏輯推理、數學建模、數學運算、直觀想象等部分。“思維品質”由蘇聯心理學家斯米爾諾夫在其著作《心理學》中最早提出，體現個體在思維活動中呈現出的不同智力特征與表現差異。具體到學科，數學思維品質則體現為學生在數學活動中的個性思維特征。數學思維品質由敏銳性、靈活性、深刻性、批判性、創造性等五個維度構成［1］。筆者從教學實踐入手，探尋核心素養下小學數學思維品質的培養路徑。

一、從數學運算著手，培養學生數學思維敏銳性

數學運算是指運用數學相關公式法則，正確進行運算的綜合能力。運算能力是一種數學思維能力，它是學生數學素養的核心。能否恰當掌握數學算理，能否通過合理簡潔的運算途徑來解決數學問題，是衡量學生數學思維品質優劣的重要指標，也是培養數學思維品質敏銳性的重要通路。我們要重視學生運算能力的培養，重視數學運算與思維敏銳性之間的關聯，增強學生數學學習的敏感性。

加減法是數學運算的開始，也是低年級學生面對數學課程時最先學習的內容。看似簡單、機械的加減運算學習中，實際蘊藏著對數學思維敏銳度的考察。在教學蘇教版小學數學一年級上冊《10 以內的加法和減法》時，有這樣的一道練習題：8-3+2=？課堂練習中，有的學生這樣計算：8-3=5，然后用5 和2 相加，得數是7，從而求得正確答案。但一些學生則敏銳地觀察到8 和2 之間的“整十”關系，將運算過程簡化為：8 和2 的和，然后再減去3，即8+2-3=10-3，從而求得題目答案7。我們知道，“運算律”是小學四年級才接觸的學習內容，但在低年級數學運算課堂上，這樣的思維敏銳度會經常發生，需要我們在教學中百般呵護。

二、從邏輯推理著手，培養學生數學思維靈活性

邏輯推理能力貫穿于整個數學學習過程，是數學學科的基本思維。邏輯推理需要學生借助已有數學經驗和數學知識，按照既定規則，通過歸納、類比、證明、計算過程，尋求問題解決的過程。邏輯推理沒有固定模式可以借鑒，憑借的是解題者的數學經驗和數學直覺，體現了數學思維品質中的靈活性特點。要重視從邏輯推理著手，著眼于學生思維靈活性培養，以全面提升學生數學核心素養［2］。

在三年級《兩、三位數乘一位數的估算》一課中提供了這樣的問題情境：西瓜每箱48 元，哈密瓜每箱62 元，張大叔帶了200元，買4 箱西瓜夠嗎？300 元夠買5 箱哈密瓜嗎？本題看似一個簡單的應用題，實則反映出對學生基本邏輯推理能力的考察。常規解題思路是：（1）48×4=192（元），192 ＜200，所以，夠；（2）同理：62×5=310（元），310 ＞300，所以，不夠。一些思維靈活學生在嚴密邏輯推理基礎上想到估算的方法解題，取得異曲同工之妙：（1）48 看成50，50×4=200（元），48×4 ＜200，所以，夠；（2）同理：62 看做60，60×5=300（元），62×5 ＞300，所以，不夠。由此可見數學思維的靈活，建立在嚴謹的邏輯推理基礎之上，值得我們在小學數學課堂教學中認真總結應用。

三、從數學抽象著手，培養學生數學思維深刻性

數學抽象是利用數學概念、原理或方法等解釋現實生活中數學問題的過程。數學抽象能力體現了學生由生活經驗向數學問題遷移的思維過程，是學以致用和數學思維深刻性的體現。數學教材中的各種應用題型、圖形與數量轉換題型，均包含著大量對數學抽象思維的考量。實際教學中，我們要重視類似題型在日常課堂中的應用，以凸顯它們對學生數學思維深刻性的影響和培養。

以四年級下冊《解決問題的策略》例2 的教學為例：有一塊長方形的草地，長8 米，在后期改建中，草地的長度增加了3米，面積相應增加了18 平方米。請問，原來的草地面積是多少？本題是將學生們常見的生活場景進行數學抽象處理的代表，考查學生對具體問題的數學抽象處理能力。按照題目意思分析，學生們通過作圖很快找到解題思路：18÷3=6（m），8×6=48（m2）。但也有同學發現：在同樣的寬度情況下，大的未知長方形面積與小的已知長方形面積（18m2）間的關系，應該是8 和3 大小關系的反應，即8÷3×18=48（m2），既是對小學六年級數學“等比例”思維的提前應用，也體現了在數學抽象能力應用過程中的思維深刻性。

四、從數學建模著手，培養學生數學思維批判性

建模能力是從不同數學情境中抽離出具體數學問題，通過數學符號、數學公式以及數學理論，進行模型構建的過程。數學建模體現了數學學習中的應用能力，在探尋數學模型間的數量關系和變化規律過程中，學生會自發反思對數學知識的掌控能力，提升數學思維中的批判能力，增強數學學習興趣，進而提升數學思維品質和核心素養能力。

以四年級下冊《三角形、平行四邊形和梯形》這一單元中的一道題為例：把一根長為14cm 的吸管，剪成3 段，要求每段都是整厘米數，拼成三角形，請問：有多少種剪法。題目先行進行了示例：剪成3 厘米、5 厘米和6 厘米的三段，3+5+6=14cm。本題的核心是對三角形圖形中三邊關系知識點的考察，解決此題的關鍵，是在熟稔上述知識點基礎上，基于三角形三邊關系構建解題模型：（1）兩邊之和大于第三邊，那么，14÷2=7，任何一個邊長，都不可以大于7；（2）假設長邊為6，則還剩余8，可以分為：（4，4）（3，5）（2，6）等三種情況；（3）假設長邊為5，則還剩9，可以分為（4，5）；（4）若長邊為4，則尚余10，10÷2=5＞4，4 為長邊的說法不成立。因此，最終還可以組成三角形有以下幾種情況：（1）6，4，4；（2）6，2，6；（3）5，4，5 等三種形式。通過本題的學習，同學們在動手動腦嘗試各種剪法的同時，也在反思自己對三角形邊長關系的認知，在數學建模的解題過程中，形成數學思維的批判性吸收，以促進學生積極健康的數學核心思維養成。

五、從直觀想象著手，培養學生數學思維創造性

直觀想象是學生借助個人經驗，通過直覺判斷，將復雜的數學問題變得簡明、形象，從而獲取解決數學問題的思路，或直接預測出數學結果的過程。注重直觀想象力培養，不僅是數學核心素養的前提，也有助于學生數學思維創造性提升。

以下題為例：將兩個相同的直角梯形疊合在一起（如下圖1中圖a 所示），求陰影部分的面積。正常的解題思維，是進行圖形切割，將下圖圖a 中的不規則陰影圖形進行規則切分，以探尋解題之路。在課堂教學中，通過鼓勵學生認真讀題，充分發揮圖形想象力，借助數學直觀思維，探尋解題之道。經過幾輪討論，學生們很快發現了該題的解題思路：去除兩個相同圖形的重疊部分面積，陰影面積可以等價替換為圖b 陰影部分面積，借助梯形公式，［（10-2）+10］×6÷2，很快得出結果54。

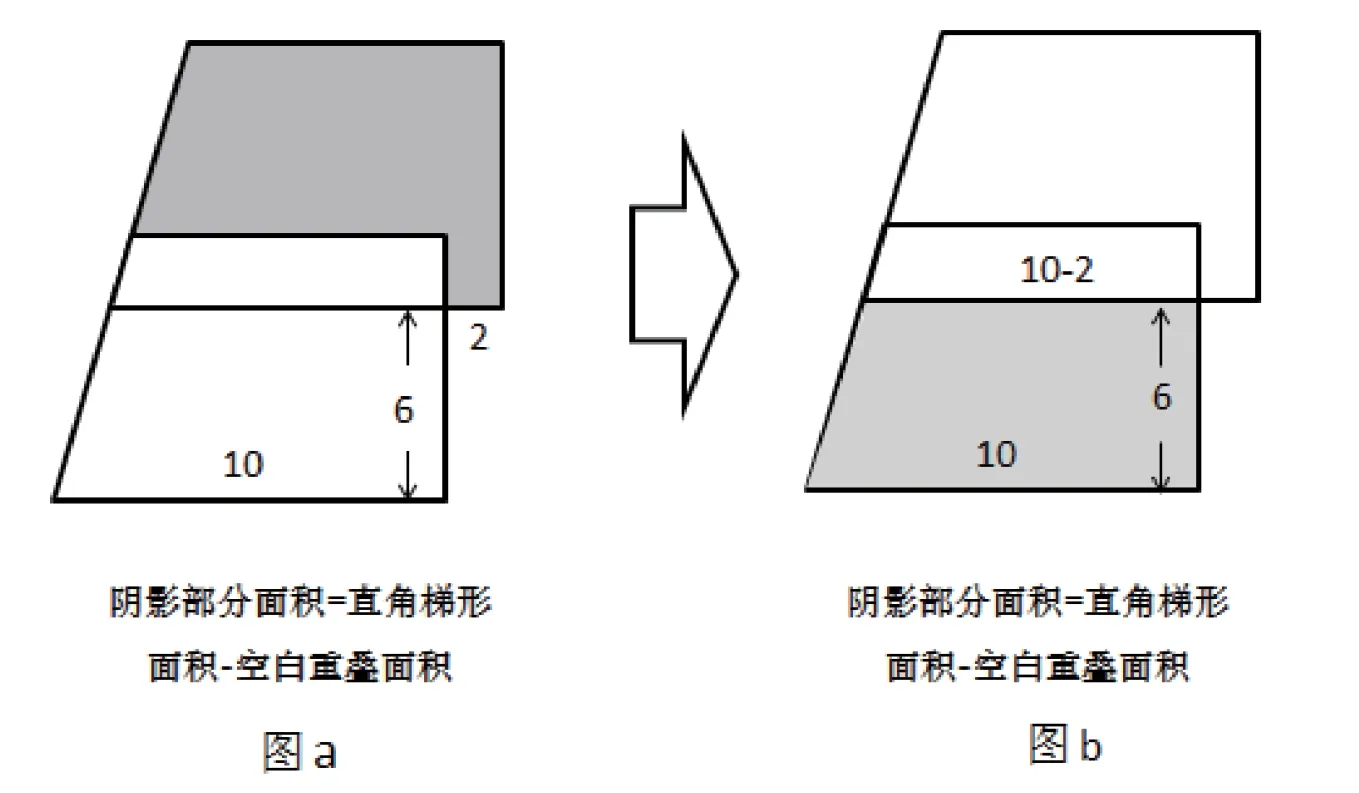
圖1

總之，核心素養下，要聚焦學生思維品質的培養，只有在每一節課中夯實學生基礎，循序漸進不斷滲透，與時俱進，運用新的教學方式，精心設計課堂教學，充分調動學生的主動性，才能培養出小學生優秀的數學思維品質。