利用“對稱性”巧解碰撞問題

李維富

（云南省昭通市第一中學(xué)）

碰撞問題是動(dòng)量守恒定律應(yīng)用中的經(jīng)典問題.在求解碰撞后的速度時(shí)，如果是完全非彈性碰撞，計(jì)算會(huì)很簡單，但如果是彈性碰撞，涉及二元二次方程組的求解，計(jì)算難度比較大.通過分析，可以看出彈性碰撞中蘊(yùn)含“等差數(shù)列”的思想，彈性碰撞是關(guān)于共速時(shí)刻“對稱”的，利用這種“對稱性”可以很容易地對碰撞后的速度進(jìn)行求解，對這種“對稱性”進(jìn)行拓展運(yùn)用，還可以快速分析其他一些碰撞類問題.

1 問題的引出

例1如圖1所示，在光滑水平地面上，質(zhì)量分別為m1＝3kg、m2＝1kg的A、B兩小球分別以速度v1＝10m·s－1、v2＝2m·s－1開始同向運(yùn)動(dòng)，發(fā)生彈性碰撞，求碰后的速度v′1和v′2.

圖1

分析在彈性碰撞過程中，遵循動(dòng)量守恒定律和機(jī)械能守恒定律，所以有

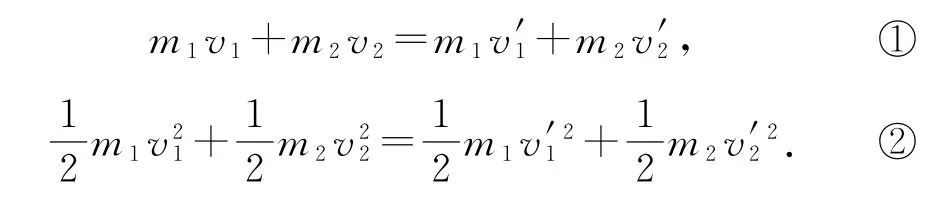
聯(lián)立上面兩式求得

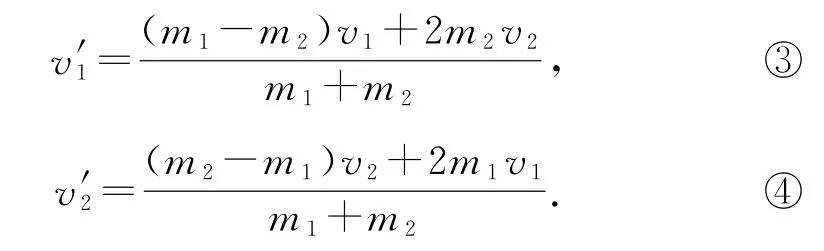
將數(shù)據(jù)代入式③④可得

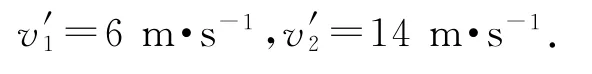
解決上述例題需要學(xué)生求解二元二次方程組，比較困難，所以經(jīng)常要求學(xué)生記住③④兩式.然而在教學(xué)過程中發(fā)現(xiàn)，很多學(xué)生記不住，即使記住了也很可能混淆.能不能找到一種既不需要記公式又能快速求解的方法呢?答案是“能”.

2 對于彈性碰撞問題的巧妙解答

在圖1的碰撞情境中，根據(jù)碰撞條件可知，兩小球碰撞之前有v1＞v2，碰撞之后有v′1＜v′2，由此可推知在碰撞過程中一定有個(gè)時(shí)刻兩小球速度相等，設(shè)為v共.根據(jù)碰撞全程動(dòng)量守恒，可得

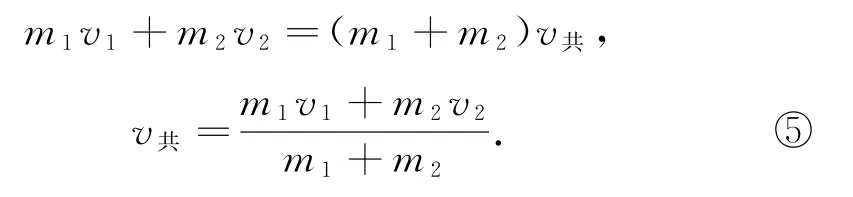
根據(jù)數(shù)學(xué)關(guān)系可看出上述的v1、v共、v′1構(gòu)成等差數(shù)列，公差為還可以看出v2、v共、v′2也構(gòu)成等差數(shù)列，公差為.利用這一思想，可以快速計(jì)算前面例1中的問題.

由式⑤可以算得v共＝8 m·s－1，再由v1、v共、v′1構(gòu)成等差數(shù)列，可得v′1＝6m·s－1.同理可得

式⑤相比式③、④要好記得多，也可以不用記憶，直接根據(jù)動(dòng)量守恒定律快速求解出v共，然后再利用等差數(shù)列的思想快速求解碰后速度v′1和v′2.

3 關(guān)于“等差數(shù)列”的思考

對于“等差數(shù)列”的思想，還可以換個(gè)角度來證明.在圖1的碰撞情境中，根據(jù)彈性碰撞的特點(diǎn)，我們得到了①、②兩式.

式①變形可以得到

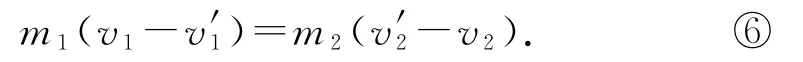
式②變形可以得到

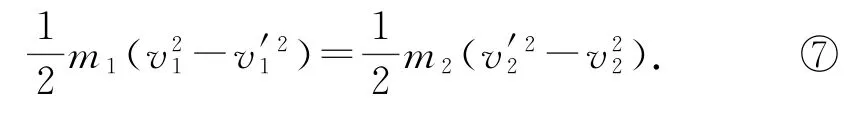
用⑦÷⑥可得到v1＋v′1＝v2＋v′2，或改寫成

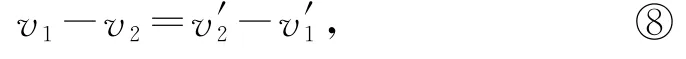
式⑧中v1－v2代表碰前A、B兩小球相互靠近的相對速度，v′2－v′1代表碰后兩小球逐漸遠(yuǎn)離的相對速度，二者相等.

在圖1的碰撞過程中，因?yàn)樾∏駻、B之間的相互作用，A會(huì)減速(也可能是減為0后反向加速)，B會(huì)加速，可將兩球碰撞過程的速度—時(shí)間(v-t)圖像畫出，如圖2所示(考慮到兩小球并不是做勻變速直線運(yùn)動(dòng)，故將之畫為虛線).

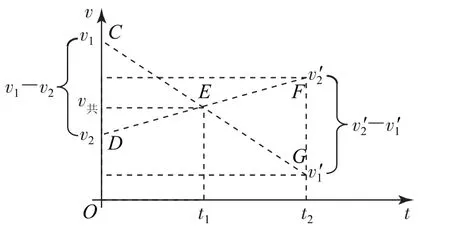
圖2

碰撞過程在0～t2這段時(shí)間完成.在這段時(shí)間內(nèi)小球A的速度從v1(C點(diǎn))減為v′1(G點(diǎn))，小球B的速度從v2(D點(diǎn))增為v′2(F點(diǎn))，在碰撞過程中的t1時(shí)刻兩小球共速(E點(diǎn)).CD段長度代表兩小球碰前的相對速度v1－v2，F(xiàn)G段長度代表兩小球碰后的相對速度v′2－v′1，前面已經(jīng)證明二者相等，由此很容易看出△CDE≌△GFE.因?yàn)椤鰿DE≌△GFE，故C、G兩點(diǎn)關(guān)于E點(diǎn)對稱，所以v1、v共、v′1構(gòu)成等差數(shù)列；同理，v2、v共、v′2也構(gòu)成等差數(shù)列.

從圖2中還可以看出，兩小球碰撞過程中共速的時(shí)刻t1剛好是整個(gè)彈性碰撞全程0～t2時(shí)間的中間時(shí)刻，彈性碰撞碰前和碰后的速度是關(guān)于共速時(shí)刻“對稱”的.

4 關(guān)于“對稱性”的拓展應(yīng)用

我們還可以換個(gè)角度來認(rèn)識碰撞類問題.

從圖2可以看出，碰撞不會(huì)在t1時(shí)刻之前結(jié)束，因?yàn)樵谀侵癆球速度大于B球速度，與碰撞情境相悖，碰撞可能結(jié)束的時(shí)刻t應(yīng)滿足t1≤t≤t2.

若碰撞在t1時(shí)刻就結(jié)束，那就是完全非彈性碰撞，碰后兩小球共速，相對速度為0.

若碰撞在t2時(shí)刻結(jié)束，那就是彈性碰撞，碰后兩小球相對速度(A對B)等于碰前相對速度(B對A).

若碰撞在t1～t2之間的某個(gè)時(shí)刻結(jié)束，則是一般的非彈性碰撞，這時(shí)A球速度還未減到v′1，B球速度還未增到v′2，兩小球的相對速度小于v′2－v′1，也就是小于碰前的相對速度.

綜上分析可知，無論什么碰撞，碰后的相對速度不會(huì)大于碰前的相對速度.

例2如圖3所示，在光滑的水平地面上質(zhì)量為m的物體A以速度v0與靜止的質(zhì)量為2m的物體B發(fā)生碰撞，則碰撞后物體A的速度大小可能是( ).

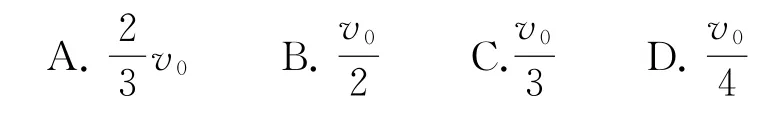
圖3

分析本題未說明A、B之間發(fā)生什么碰撞，需要分類討論.若A、B發(fā)生完全非彈性碰撞，碰后的共同速度根據(jù)動(dòng)量守恒很容易算出，為若A、B發(fā)生彈性碰撞，根據(jù)“對稱性(等差數(shù)列)”的思想可算出碰后A、B的速度分別為.因?yàn)榕鲎步Y(jié)束時(shí)刻只能在t1≤t≤t2范圍內(nèi)，借助v-t圖像，可以看出碰后B的速度范圍是同時(shí)可以看出碰后A的速度大小的范圍是的速度范圍是，如圖4所示，故選C、D.

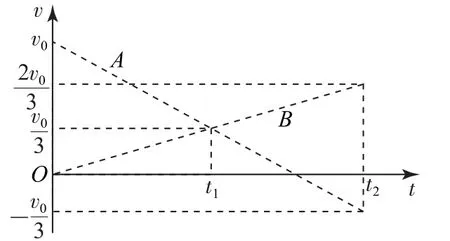
圖4

例3如圖5所示，質(zhì)量相等的A、B兩球，初始時(shí)在光滑水平面上沿同一直線相向做勻速直線運(yùn)動(dòng)，A球的速度為6 m·s－1，B球的速度為－2m·s－1，不久A、B兩球發(fā)生碰撞，對于碰后A、B速度的可能值，不可能的是( ).

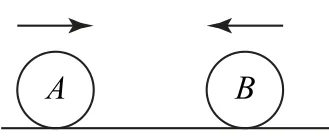
圖5

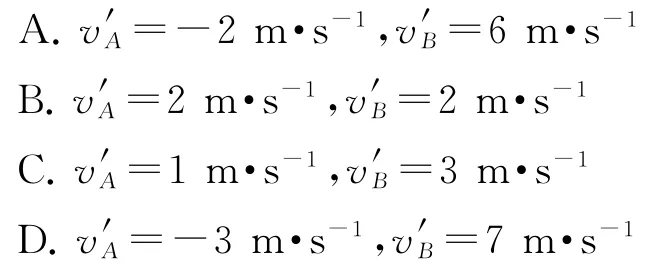
分析本題常見的解題思路是根據(jù)碰撞前后系統(tǒng)動(dòng)量守恒以及碰撞后系統(tǒng)的機(jī)械能不大于碰前的機(jī)械能聯(lián)立求解.不過這一思路計(jì)算量相對較大，建議用前面的結(jié)論去分析，因?yàn)榕龊蟮南鄬λ俣炔粫?huì)大于碰前的相對速度，所以選D.