筒式壓縮空氣彈射系統內彈道性能研究

劉南宏，張新敬，徐玉杰，5，郭 歡，馮 璐，陳海生，4，5

(1.中國科學院工程熱物理研究所， 北京 100190； 2.中國科學院大學， 北京 100049； 3.華北電力大學，河北 保定 071003； 4.畢節高新技術產業開發區國家能源大規模物理儲能技術研發中心， 貴州 畢節 551712； 5.中科院工程熱物理研究所南京未來能源系統研究院， 南京 211135)

1 引言

壓縮空氣具有高能量密度，可應用于能源存儲、彈射推進等領域。壓縮空氣彈射作為一種冷發射方式，該類彈射系統把壓縮空氣作為工作介質和動力來源，將壓縮空氣儲存的內能快速轉化為彈射體的動能，使之在短時間內獲得較大出射速度，實現能量的傳遞。此類彈射方式可通過調節系統參數，滿足對不同質量物體的彈射需求，提高推進效率，降低單位質量的發射成本。相對于其他彈射方式，如機械彈力式、燃氣式、液壓式、電磁式等，壓縮空氣彈射具有顯著優點：結構簡單、能量密度高、適用場景廣、易于維護、成本低等。

由于壓縮空氣彈射時間歷程短、多變量下彈射性能變化復雜，因此對系統進行合理的參數設計、過程變量變化規律分析及實驗驗證就尤為重要。目前，國外已將壓縮空氣彈射實現軍事或商業應用：如美國掃描鷹(ScanEagle)無人機使用的Mark 4氣壓彈射器，展開后長6.71 m、寬2.21 m、高2.44 m，質量為1 905 kg，使用溫度范圍為-17.8～48.9 ℃，兩次彈射時間距小于10 min，能夠使20 kg的無人機以25 m/s的速度發射。英國梅吉特(Meggitt)防務公司研發的“大力士”(Hercules)氣動彈射器配有16 m長的軌道，壓縮空氣壓力可達1 MPa，能夠以55 m/s的速度發射250 kg的無人機。芬蘭羅伯尼克(Robonic)公司生產的“孔蒂奧”(Kontio)第三代氣動彈射架，可適用于40～1 000 kg全系列無人機，最大發射功率可達8 500 kW，能以37 m/s的速度發射重達500 kg的無人機飛行器。國內則有學者進行了壓縮空氣彈射仿真及相關實驗研究：從龍騰等以超近程防御武器系統發射裝置為背景，利用AUTODYN建立了不同工況下的壓縮空氣彈射內彈道模型，在泄流直徑28 mm、壓縮空氣壓力35 MPa的情況下，彈射物體在400 mm位移處即能達到100 m/s的速度；Huang等介紹了一種無人飛行器楔形氣動發射裝置，分別基于拉格朗日方程和MSC.ADAMS軟件建立了動力學模型，在531 kPa的初始氣源壓力下能使20 kg重的無人機在0.22 s內達到27 m/s的速度；李軍等以大口徑火箭彈壓縮空氣發射裝置為研究對象，建立了不同空氣壓力、不同體積以及有、無泄漏的內彈道模型，分析表明0.005 m的泄漏面積會導致近1/4的能量損耗，對內彈道性能的影響較大；姚琳等設計了一款無桿氣缸噴射裝置，在最大過載和有效沖程保持不變的情況下，相比有桿裝置，導彈的發射速度提高15.8%；邵亞軍等分析了高壓空氣彈射裝置中黏性的影響，基于真實氣體效應分析，建立了考慮氣體摩擦的高壓空氣彈射內彈道數學模型，發現摩擦效應對系統造成的影響十分微小，在氣體快速、短時釋放過程中可忽略這些影響；熊鎬等研究了氣體炮內彈道膛內氣體運動及閥門的影響，在 FLUENT中利用自定義函數讀取彈體表面壓力變化，結果表明無閥門氣體炮的膛內氣體基本符合均勻分布假設，有閥門氣體炮在內彈道初期氣流存在回流現象，彈底壓力先快速上升后逐漸減小，并在一定范圍內波動，最后逐漸趨于穩定。

可以看出，在壓縮空氣彈射系統研發與應用方面，國外擁有較為成熟的產品，但其技術細節公布較少，國內開展了大量的研究工作，主要集中在理論分析以及一些關鍵過程的實驗驗證，對實際彈射過程中氣體作用機理和參數影響規律仍需更進一步的研究。

本文利用熱力學模型，對筒式壓縮空氣彈射系統進行參數設計，開展實驗研究，并建立了內彈道動態仿真模型，獲得了彈射過程中的壓力、質量、距離等參數對彈射性能的影響規律，分析了壓縮空氣彈射的作用機理，可為壓縮空氣彈射系統的工程研制提供參考。

2 壓縮空氣彈射系統設計分析

一種筒式壓縮空氣彈射系統的示意圖如圖1所示，由高壓儲氣罐、彈射筒和彈射體等部件組成。其工作原理為：彈射前，空氣經過壓縮機，被壓縮成高壓氣體，儲存在儲氣罐中；彈射時，打開閥門，儲氣罐瞬間排出大流量的高壓空氣，經連接管道，快速流入彈射筒，使得彈射體左側氣壓迅速增高；彈射筒內，通過左右壓差產生的推動力，驅動彈射體不斷加速運動，直至離開彈射筒，整個彈射過程完成。

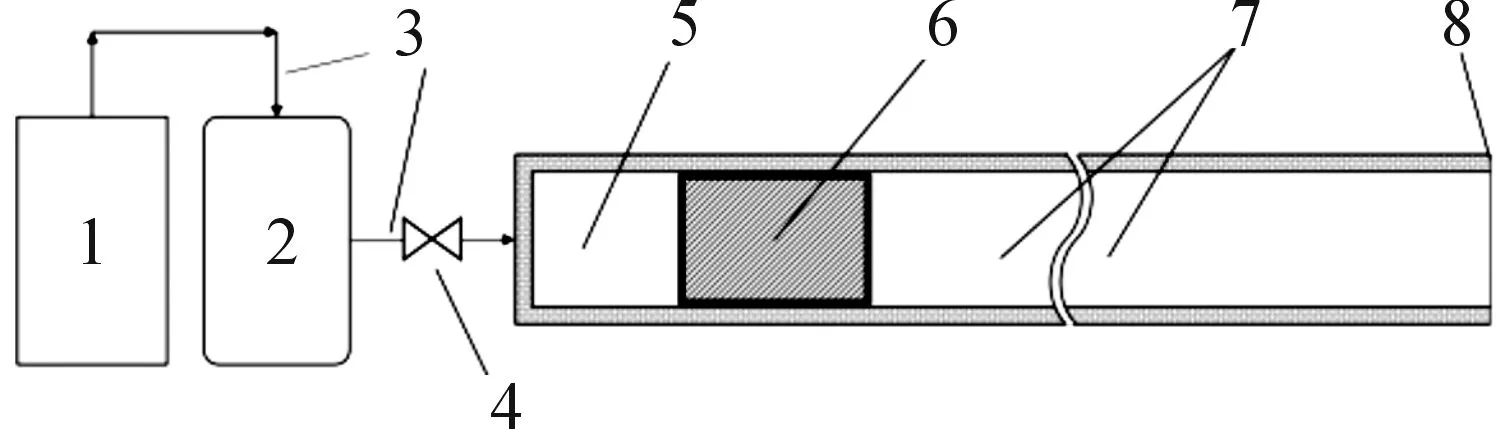
1.空氣壓縮機; 2.高壓儲氣罐; 3.連接管; 4.閥門;5.彈射筒內 高壓空氣區域; 6.彈射體;7.彈射筒內常壓空氣區域;8.出射口

本方案的設計目標：通過壓縮空氣彈射，使6 kg重的彈射體在500 kPa儲氣罐初始壓力、5 m有效彈射長度的條件下，彈射速度達到60 m/s以上。

2.1 壓縮空氣彈射系統熱力學分析

利用熱力學模型，對壓縮空氣彈射系統開展總體參數設計。為了簡化，設計基于以下假設條件：① 裝置密閉性良好，不存在漏氣現象；② 視壓縮空氣為理想氣體；③ 彈射體在運動中與管壁的摩擦因數視為恒定值。基于理想氣體狀態方程、質量連續性方程、能量守恒方程和動力學方程，建立壓縮空氣彈射系統的熱力學模型。

高壓儲氣罐釋氣時：

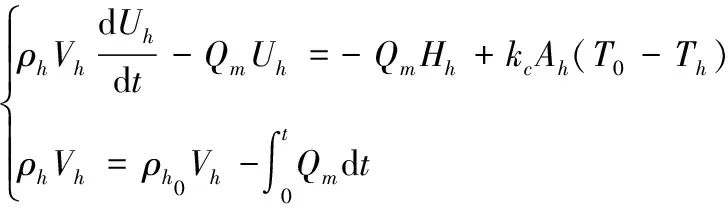
(1)

彈射筒左側低壓區域吸氣時：

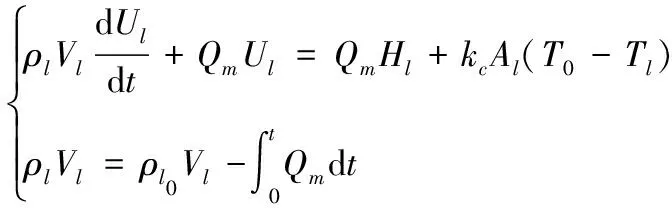
(2)

其中：為空氣密度；為氣體體積；為比熱力學能；為空氣質量流量；為氣體某時刻的絕對溫度；為空氣比焓；為氣體與外壁接觸的表面積；為傳熱系數；為時間步長。帶下標“”的參數對應儲氣罐高壓氣體，帶下標“”的參數對應彈射筒左側低壓氣體。帶下標“0”為對應區域初始參數。

高壓氣體由儲氣罐經閥門流入彈射筒低壓區的過程中，其質量流量方程可分亞聲速和超聲速2種情況：

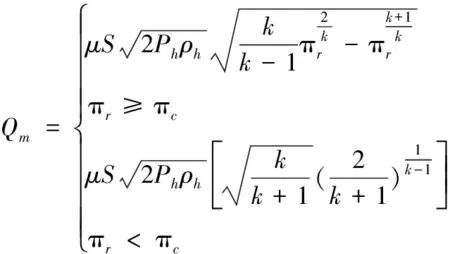
(3)

其中：為流量修正系數；為空氣流通面積；為儲氣罐空氣壓力；為空氣絕熱系數。

π為進出口壓比，表達式

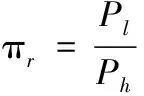
(4)

π為臨界壓比，表達式

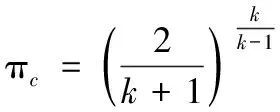
(5)

當彈射體左右區域的氣體產生壓力差，即會驅使其運動，根據牛頓第二定律，對于某一時刻，有如下動力學方程：

(6)

其中：為大氣壓力；為阻力系數；為彈射體質量；為重力加速度；為彈射體速度。

由于本壓縮空氣彈射系統為水平放置，運動過程所受阻力幾乎完全來自彈射體與管壁的摩擦力，此處簡化阻力系數等于摩擦因數，取=02。

2.2 彈射系統設計參數分析

以上述過程搭建的熱力學模型為基礎，針對質量分別約為4 kg、6 kg和10 kg的3個彈射體，采用單一變量法分析儲氣罐體積、彈射筒直徑對彈射性能的影響規律。相關參數設置如表1所示。

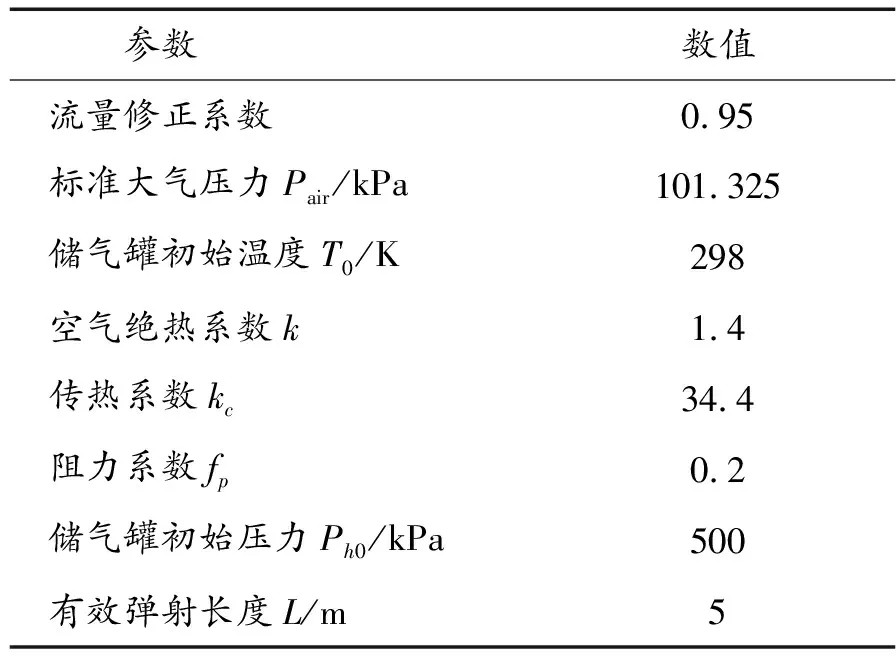
表1 熱力學模型參數Table 1 Parameters of thermodynamic model

計算結果如圖2、圖3所示。

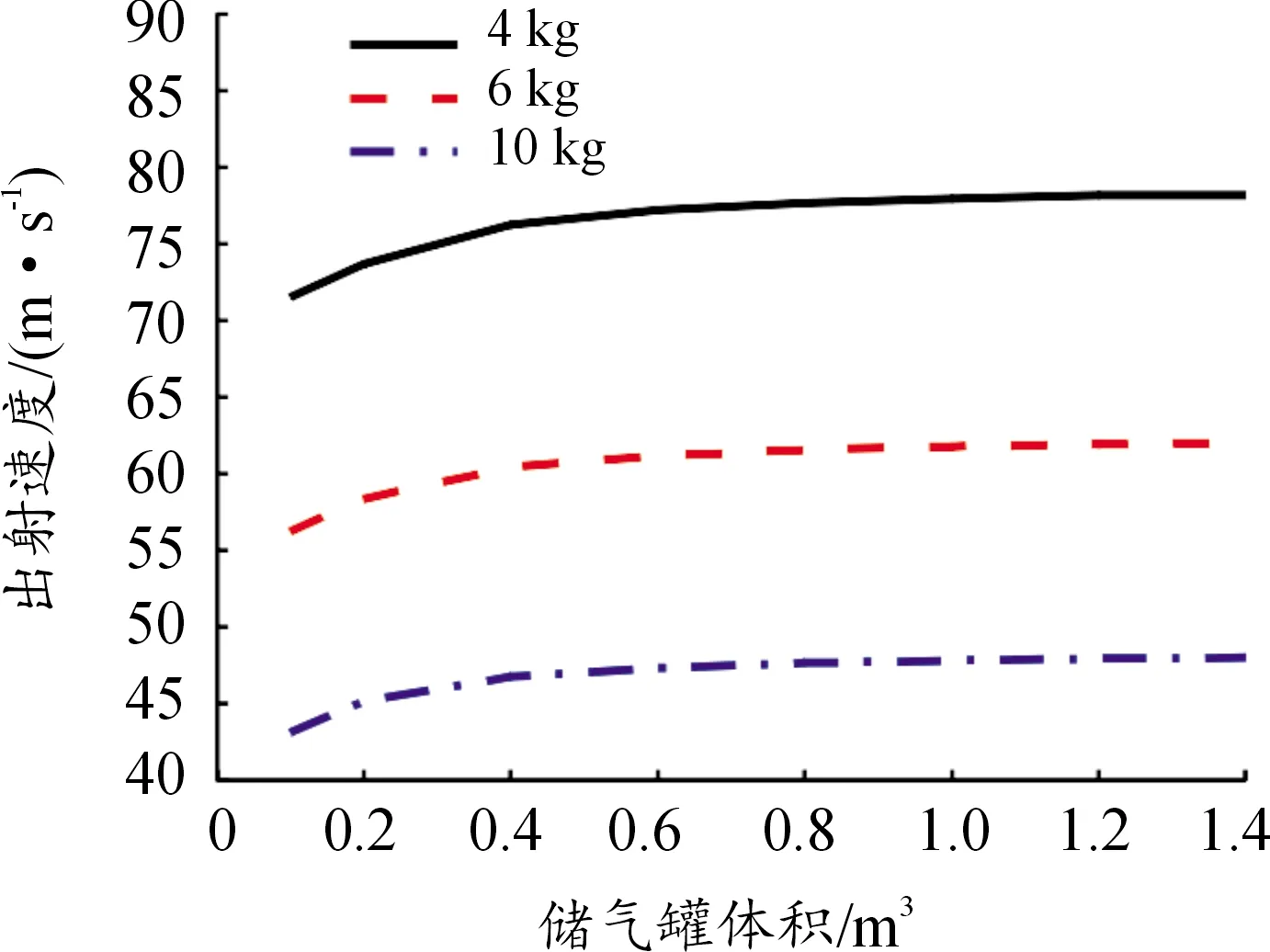
圖2 彈射體出射速度隨儲氣罐體積的變化曲線

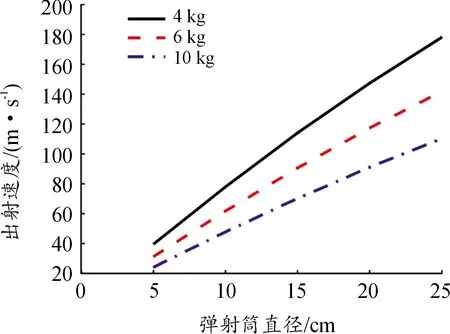
圖3 彈射體出射速度隨彈射筒直徑的變化曲線

由圖2可知，彈射體出射速度隨儲氣罐體積增加而增加，但當儲氣罐體積大于一定值后，儲氣罐體積的增加對出射速度的增益不明顯。原因是在儲氣罐體積較低時，彈射過程的氣體流動會導致儲氣罐內高壓氣體壓力迅速降低，使中后期彈射體所受推力減小，加速度減小，最終出射速度較小。儲氣罐體積增加后，儲氣罐內高壓氣體更為充足，隨著彈射過程進行，其罐內壓力變化小，驅動彈射體的高壓氣體壓力變化較小，使得彈射體的加速度幾乎不變，因此較大儲氣罐體積下的彈射體速度變化不明顯。

對于本研究設計目標，儲氣罐體積為0.6 m時即滿足要求。考慮到氣體密封性的影響，并留一定裕量，實際加工時選擇體積1 m的儲氣罐。

由圖3可知，彈射體出射速度隨彈射筒直徑增加而增加，且大致呈線性趨勢。在其他條件不變的情況下，更大的直徑會增加彈射體與空氣的接觸面積以及空氣流量，使彈射體加速度和出射速度隨之增加。

對于本研究設計目標，彈射筒直徑為10 cm的時候即可滿足要求。

3 彈射實驗及仿真對比

3.1 壓縮空氣彈射實驗

水平放置的筒式壓縮空氣彈射系統示意圖和實物圖如圖4、圖5所示，主要由高壓儲氣罐、截止閥、快速氣動閥、彈射筒、彈射體和支撐結構等部分組成。

實驗時，加工出的彈射體實際質量分別為：3.961 kg、6.336 kg和10.609 kg。

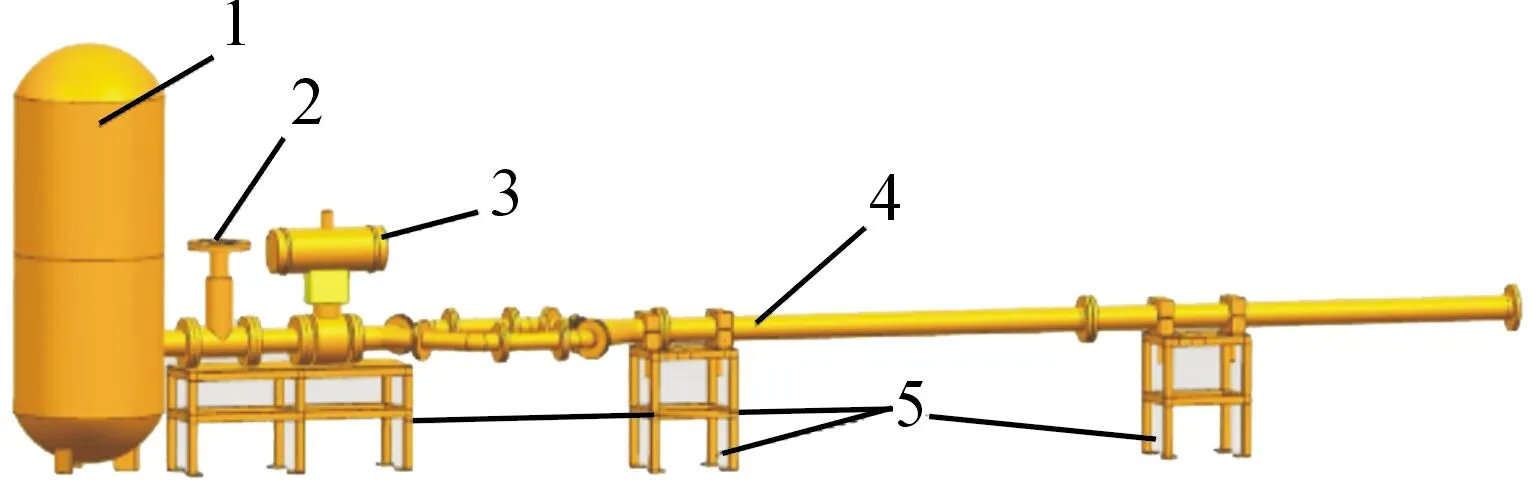
1.高壓儲氣罐; 2.截止閥; 3.快速氣動閥; 4.彈射筒(彈射體位于筒內); 5.支撐結構

圖5 壓縮空氣彈射實驗臺集成場景圖

3.2 動態仿真模型

本文中的壓縮空氣彈射系統，采用動力學分析軟件實現彈射過程的內彈道模擬仿真。針對彈射模型中功能不同的各個部件，將其簡化為4個部分：儲氣罐模型、彈射筒模型、彈射體模型和外壁模型。以6.336 kg彈射體為例，搭建好的壓縮空氣彈射動態仿真模型示意圖(尺寸單位：mm)如圖6所示。

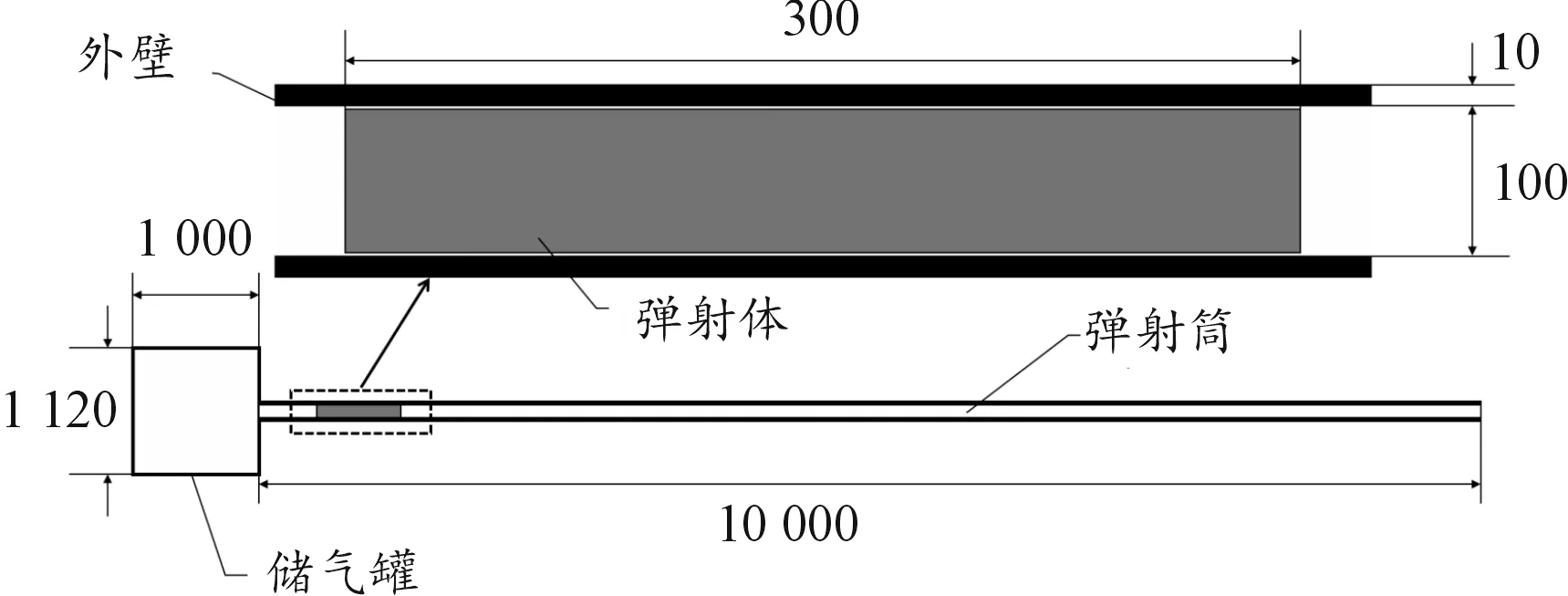
圖6 壓縮空氣彈射動態仿真模型示意圖

其中，在儲氣罐中填充高壓空氣，在彈射筒中填充常壓空氣，彈射體與外壁均采用鋁材料。

3.3 網格無關性驗證

根據壓縮空氣彈射系統的物理尺寸，結合仿真模型的網格劃分情況，此處選擇采用2 mm、5 mm、7 mm和10 mm的網格尺寸進行網格無關性驗證。

圖7為網格無關性計算結果，可以看出，5 mm網格的模型與2 mm網格的模型結果接近。綜合考慮計算精度和計算耗時，本彈射仿真模型采用5 mm網格尺寸進行后續建模計算。

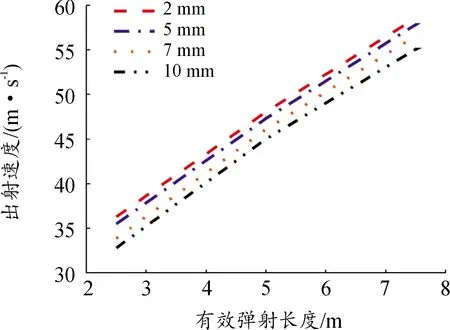
圖7 同一工況下不同網格尺寸仿真曲線

3.4 實驗結果

圖8為仿真與實驗結果曲線，以質量6.336 kg的彈射體為例，選取不同的儲氣罐初始壓力，獲取在不同彈射長度下的速度變化情況。

通過對比可以發現仿真與實驗結果擬合較好，整體趨勢一致，單個工況仿真與實驗結果誤差比例在7.0%以內，驗證了該動態仿真模型的有效性，能夠通過該方法對彈射過程進行詳細分析。

圖8 仿真與實驗結果曲線

4 壓縮空氣彈射過程分析

對于確定了儲氣罐體積和彈射筒直徑的彈射系統，不同工況下，初始參數只在儲氣罐初始壓力和彈射筒長度上存在差異，此處選擇6.336 kg彈射體在約500 kPa儲氣罐初始壓力、7.5 m彈射筒長度下的工況作分析。

除了精彩絕倫的中國歷代木雕，世界范圍內的木雕藝術，身披神秘異域面紗，其特殊的價值，也讓木雕藝術家浸潤其中。無論是南美洲原住民的詭魅木刻，埃及古老墓葬中的人像，分布廣泛的印第安種族的木雕圖騰柱，以及東南亞諸國、非洲諸國狂野與信仰兼備的民間木雕……無一不是筆者探索研究的對象。處于宗教、巫術等目的的作品，常常不刻意糾結細節，而是將整體的魅力通過粗獷的手法，將生命細胞無限延展。將人與自然的性情，引入原始的本真。材料的張力與藝術家的創想，貫通氣象，意蘊深厚，感染力強大深邃，它們穿越了歷史的屏障，帶給我們一次次心靈的洗禮。

4.1 氣體壓力變化分析

圖9為彈射過程中儲氣罐壓力曲線。

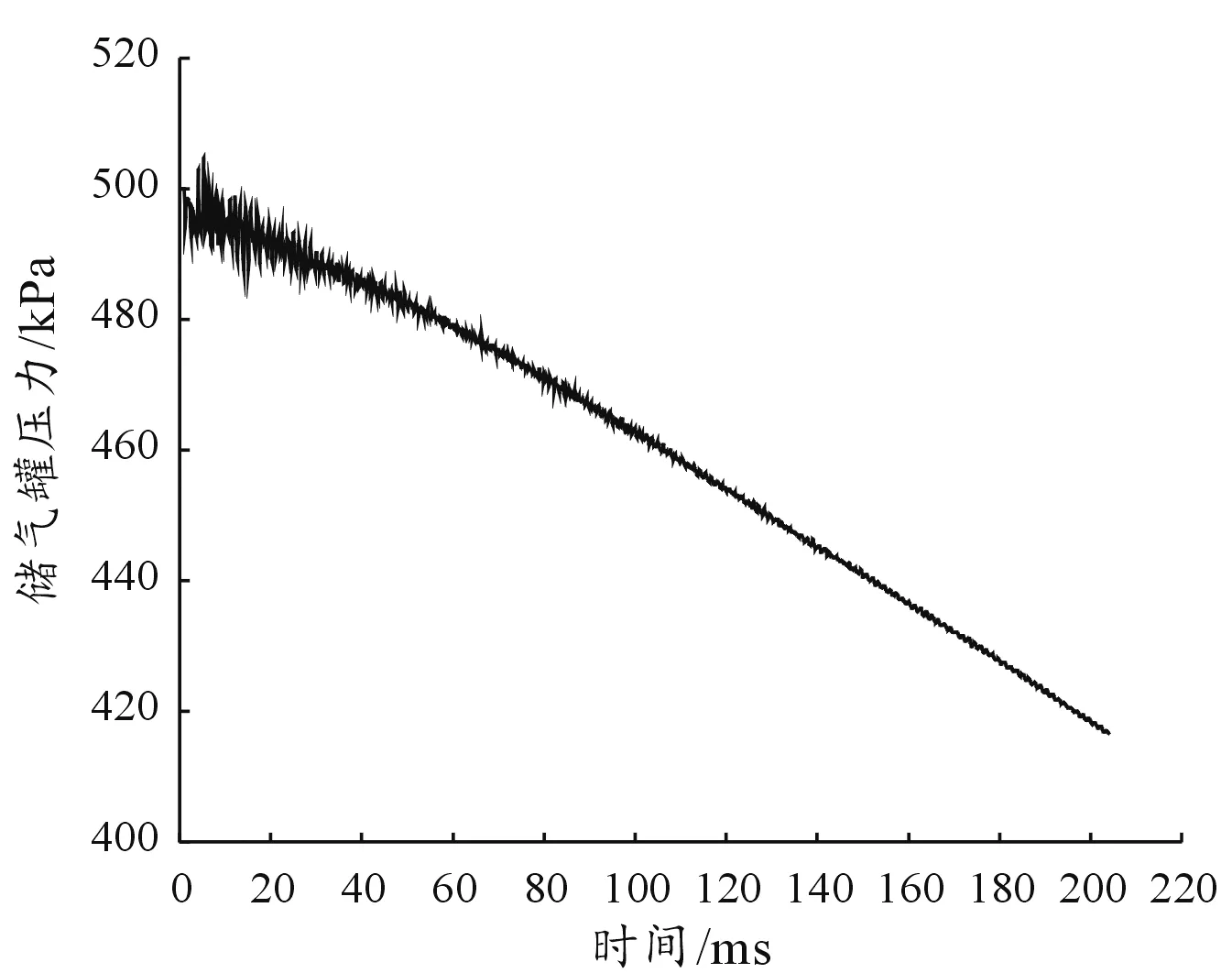
圖9 儲氣罐壓力曲線

由圖9可知，儲氣罐壓力在彈射初期波動較大，而后呈下降趨勢。初期波動是由于彈射起始時刻罐內高壓空氣迅速流動，當氣流抵達彈射體時，彈射體處于靜止狀態，高壓空氣發生滯止，壓力升高；而后彈射體移動，氣體流速增加，壓力降低，此時彈射體的速度較低，氣體流速在彈射體左側減速，壓力升高；如此反復，從而出現彈射初始時期的壓力波動。隨后，彈射體速度增加，儲氣罐高壓氣體不斷流向彈射筒內，其壓力也隨之不斷下降。

在動態仿真模型中提取彈射筒內3個不同彈射距離處(2.5 m、5.0 m和7.5 m)的空氣壓力值進行分析，壓力曲線如圖10,可知：

彈射體右側的彈射筒區域內空氣初始壓力均為101.3 kPa(即一個大氣壓)，在彈射初期某時刻壓力迅速上升，其原因是當彈射體開始運動，會帶動右側常壓空氣擠壓，短時間內壓力升高，運動相對穩定后，壓力值穩定在170 kPa左右。3條曲線均在某個時刻壓力小幅徒增后，瞬間下降為零，其原因是當彈射體靠近探測點時，彈射體右側表面附近空氣受壓嚴重，該點處的壓力會有所上升，在彈射體運動至探測點位置時，彈射體覆蓋了該空氣區域，使探測點處氣體壓力為0。彈射體通過后，壓力瞬間增至450 kPa左右，此壓力值即來自儲氣罐的壓縮空氣，作為動力源驅使彈射體加速運動。

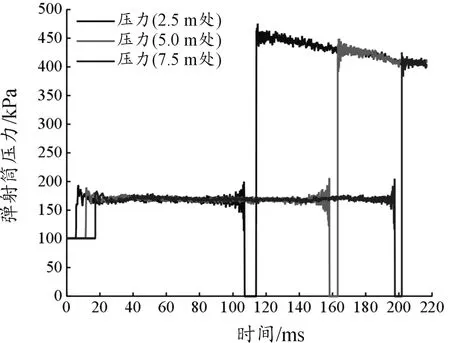
圖10 彈射筒壓力曲線

4.2 彈射體運動參數分析

提取彈射體在各個時刻的運動參數進行分析，其位移、速度、加速度曲線如圖11～圖13。

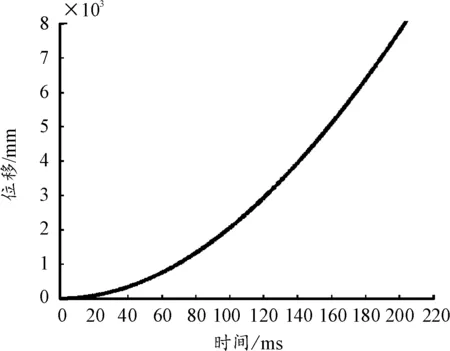
圖11 彈射體位移曲線

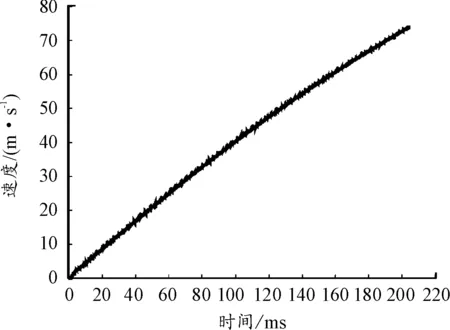
圖12 彈射體速度曲線

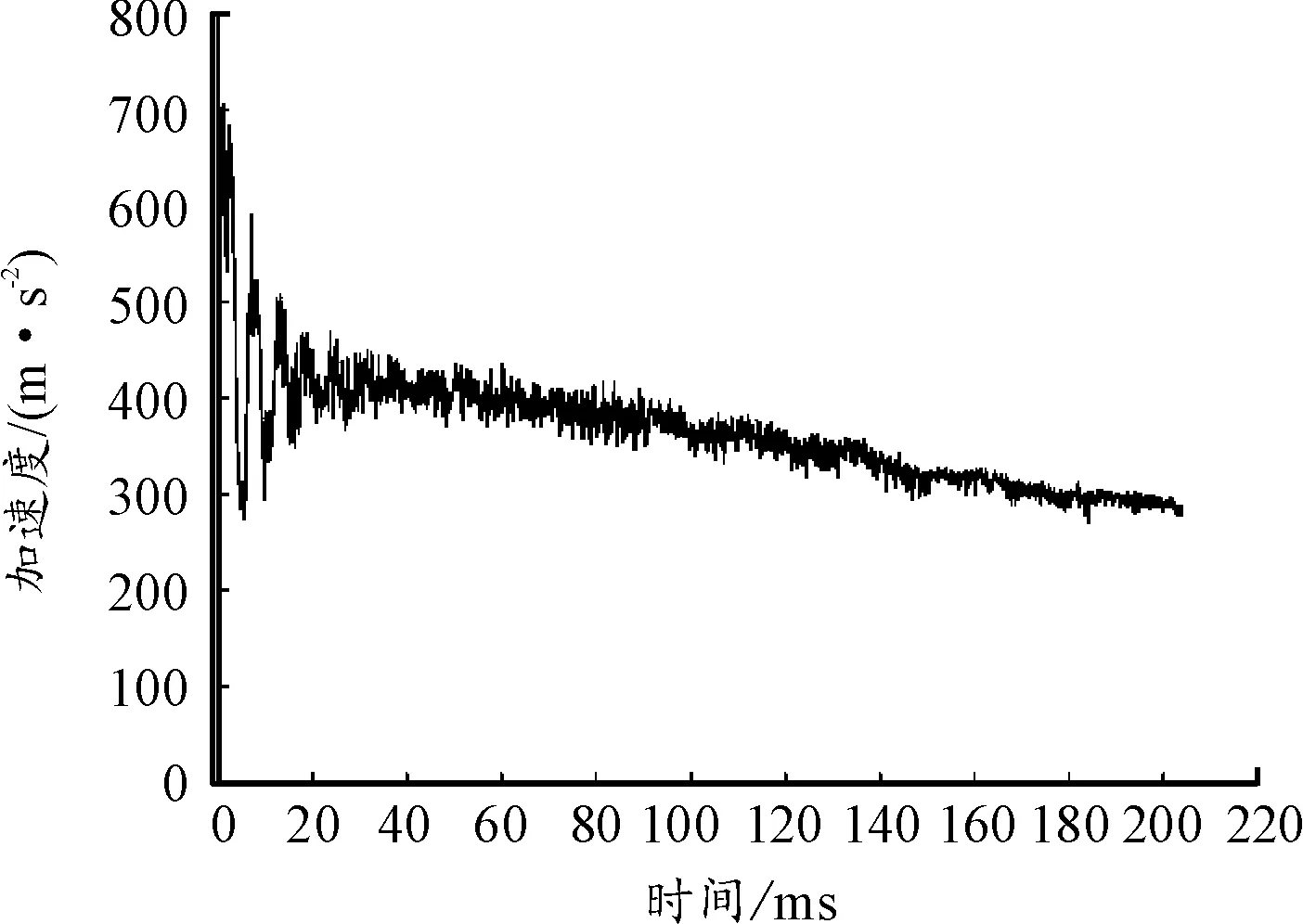
圖13 彈射體加速度曲線

由圖11可知，彈射體在方向的位移與時間大致呈二次函數關系，初始階段，彈射體由靜止狀態開始運動，運動速度較低，然后逐漸加速，該曲線斜率逐漸增加。

由圖12可知，彈射體在方向的速度與時間大致呈線性關系，其速度逐漸增加。結合圖13的加速度曲線，總體上初始階段彈射體加速度變化較小；在彈射末尾階段，由于氣體壓力變小，加速度降低。

如圖13所示，彈射初期，高壓空氣快速流動到與彈射體左側表面接觸時速度非常大，致使其動壓也很大，此時與彈射體表面發生接觸，高壓空氣有滯止現象，動能全部轉化成壓力能，速度降為零且靜壓達到最大值，而彈射體右側為常壓空氣，彈射體左、右側壓力差達到最大值，加速度達到最大值。而后，加速度在短時間內有較大波動，原因是當彈射體表面附近的高壓空氣發生滯止，壓力急劇升高，管道內壓力分布不均勻，會引發回流，致使彈射體表面附近高壓空氣壓力又迅速降低，彈射體加速度隨之降低。在回流抵達儲氣罐附近時再次滯止，使得高壓空氣重新向彈射體流動，重復上述過程，彈射體加速度又迅速升高。如此往復波動數次后，彈射過程呈相對平穩狀態。

彈射過程大致平穩后，加速度穩定在某個范圍內，伴有小幅波動，總體呈下降趨勢。原因是彈射體左側的高壓空氣壓力值隨著其總體積的增大而減小，加速度隨之緩慢減小；但由于筒內空氣的波動未能完全平穩，因此加速度仍會有細小波動。

4.3 壓縮空氣流動過程分析

圖14～圖16為彈射過程中彈射筒內部截面上半部分的速度、壓力等的分布情況。

圖14顯示，在壓縮空氣釋放瞬間，由于壓差大，壓縮空氣流動迅速，最大速度近300 m/s，在靠近彈射體左側附近存在壓力梯度，表明此時壓縮空氣未抵達彈射體端面。

圖15顯示了初始階段彈射筒內壓縮空氣的壓力分布與速度分布隨時間的變化。在0.51 ms，彈射體幾乎為靜止狀態，壓縮空氣開始在彈射體左側集聚，該區域壓力升高；在0.69 ms，高壓區域擴大，流速減小；在0.77～0.96 ms，彈射體左側集聚的壓縮空氣在壓差作用下，一部分向左回流，一部分經彈射體與彈射筒的間隙泄露，此時彈射體左側區域壓力下降。與圖13對應時刻加速度波動趨勢一致。

圖14 接觸瞬間速度云圖(0.42 ms)

圖15 壓力云圖與空氣速度矢量圖(0.51～0.96 ms)

圖16為彈射末尾階段的壓力云圖，從圖16中可知，此時彈射已趨于平穩，彈射體左、右側的空氣壓力均勻，該階段彈射體加速度較為穩定，沒有初始階段大幅波動的現象。

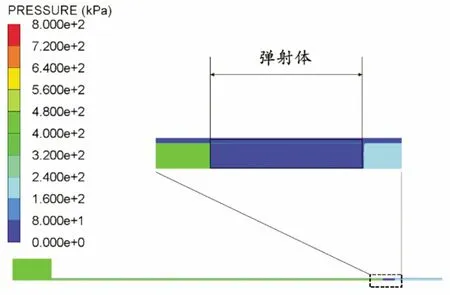
圖16 彈射末尾階段壓力云圖(198.70 ms)

5 結論

通過構造熱力學模型初步設計，得到彈射體出射速度受儲氣罐體積、彈射筒直徑的影響變化規律，綜合考慮多種因素，選擇儲氣罐體積為1 m、彈射筒直徑為10 cm。

通過彈射實驗研究，獲得了彈射過程參數變化規律。動態仿真模擬，結果與實驗結果吻合較好。獲得了彈射過程儲氣罐、彈射筒空氣壓力和彈射體各個性能參數曲線和分布云圖，分析了不同時刻下彈射體加速度與空氣壓力之間的作用過程和彈射運動機理。