搖擺作用下艦炮指向運動誤差補償分析

張滿慧，姚 忠，夏方超，張建斌

(西北機電工程研究所， 陜西 咸陽 712099)

1 引言

為滿足未來海上高技術戰爭需求，精確打擊功能要素對于艦炮已經越來越重要。艦炮精確打擊的實現不僅取決于目標定位精度，更與射擊諸元精度有關。通過解彈道方程進行艦炮射擊諸元求解時，艦船搖擺運動導致目標相對艦炮射擊中心的運動狀態發生變化，引起的艦炮指向擾動對求解過程產生較大的影響。因此，有必要明確搖擺作用下艦炮指向擾動規律，并將它作為穩定系統的動力學環節進行補償，以獲得正確完整的艦炮射擊諸元。

目前，國內外學者對艦船搖擺條件下艦炮射擊諸元求解模型進行了大量的研究，基于二分法和落點諸元信息的彈道解算方法等研究較為成熟。但是，現有研究大多直接采用艦船搖擺角獲得實際瞄準角或搖擺誤差角，卻較少考慮地球慣性系和艦船非慣性系的變換關系，沒有完全消除艦炮指向運動誤差疊加形成的射擊諸元誤差，在搖擺補償時也鮮有計及彈丸初始擾動的影響。針對該問題，本文面向艦炮多體系統的串聯運動鏈，建立了搖擺作用下的艦炮指向運動誤差模型，明確炮口指向在靜水—搖擺條件下的絕對誤差及相對誤差。從串聯機構角度構造了艦炮位姿補償模型，從目標方位一致性角度推導了炮口姿態補償模型，從彈道軌跡預測角度給出了艦炮射擊瞄準點的補償解算流程。通過仿真驗證獲得了搖擺條件下艦炮指向誤差補償特性，為各類精確打擊狀態的艦炮射擊諸元解算提供參考。

2 搖擺作用下艦炮指向運動誤差模型

基于多體系統方法，首先建立艦船搖擺條件下的艦炮串聯運動鏈如圖1所示。其中，慣性系{}原點設置在艦船搖心處，并假定隨艦船勻速運動。艦體系{}原點初始與搖心重合，指向艦艏方向，沿著甲板法向，按右手法則建立，此處主要計及對艦炮影響最大的橫搖、縱搖和垂蕩運動。艦炮系{}的原點與甲板炮位中心重合，軸向與艦體系的坐標軸一致。工具系{}原點位于炮口中心，正向與身管軸向一致，正向位于身管(射擊平面)縱截面且與垂直，按右手法則建立。

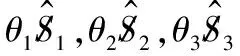
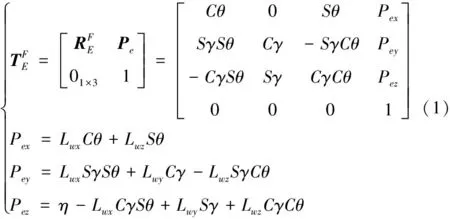
式(1)中：，，是在艦體系{}的位置坐標；符號縮寫=cos，=sin。

根據旋量坐標不變性，采用指數積公式給出艦炮工具系{}相對艦炮系{}的位姿變換矩陣模型為：

()=exp()exp()exp()(，，)

(2)

式(2)中：exp(·)是運動旋量的指數積算子；(·)是初始位姿矩陣，、、是工具系原點在艦炮系的位置坐標，并且分量通常假定為零值；、是轉動關節變量，是移動關節變量，初始都為零值。

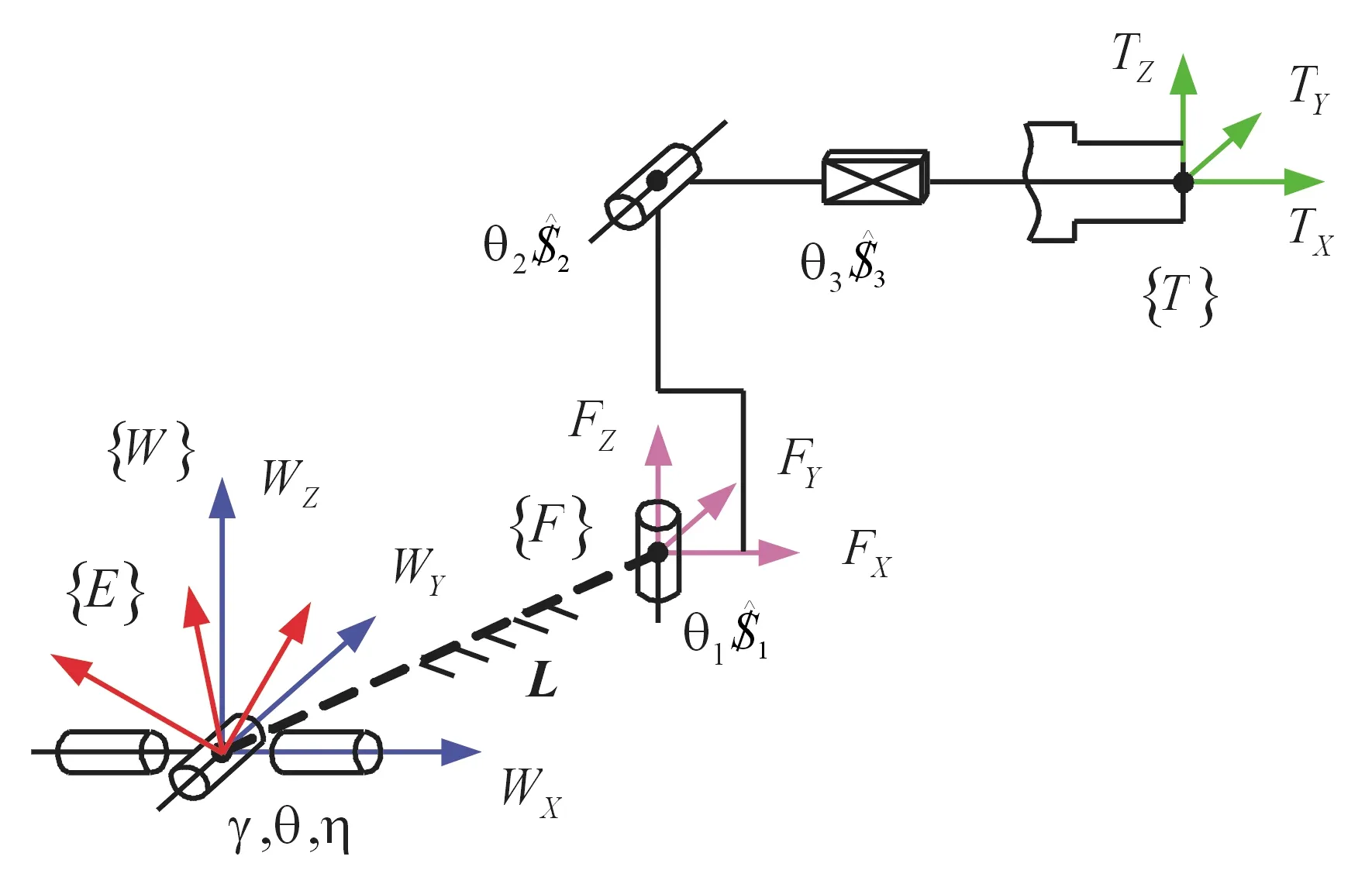
圖1 基于多體系統的艦炮串聯運動鏈示意圖Fig.1 Serial kinematic chain model of naval gun

根據坐標變換關系，推導出搖擺作用下，工具系{}相對慣性系{}的位姿模型為：

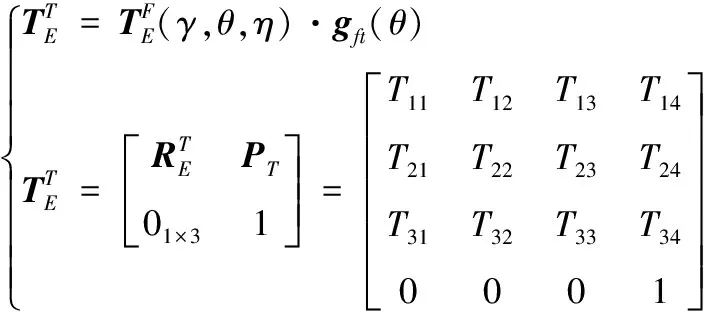
(3)

式(3)中，各矩陣元素分別為

(4)

為再明確艦船搖擺引起的指向擾動，構造出靜水條件下，工具系{}的位姿模型為：

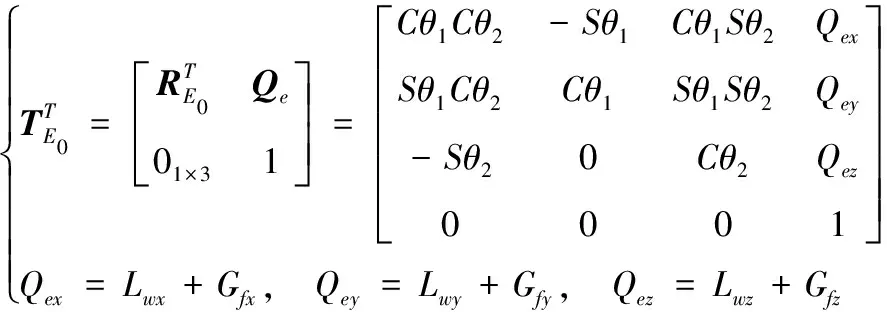
(5)

此時，根據式(3)和式(5)推導出慣性系中炮口中心擾動Δ、Δ、Δ及指向擾動、、分別為：

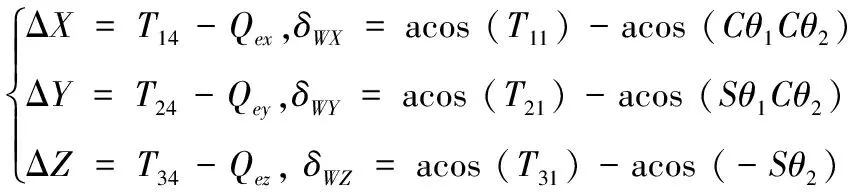
(6)

式(6)給出了慣性系中的艦炮指向誤差模型，代入艦炮瞄準跟蹤或發射時的艦炮運動變量，即可獲得搖擺作用下炮口最大可能擾動域。

為便于誤差合成分析，再采用誤差旋量對慣性系描述的工具系位姿誤差進行轉換，如圖2所示。

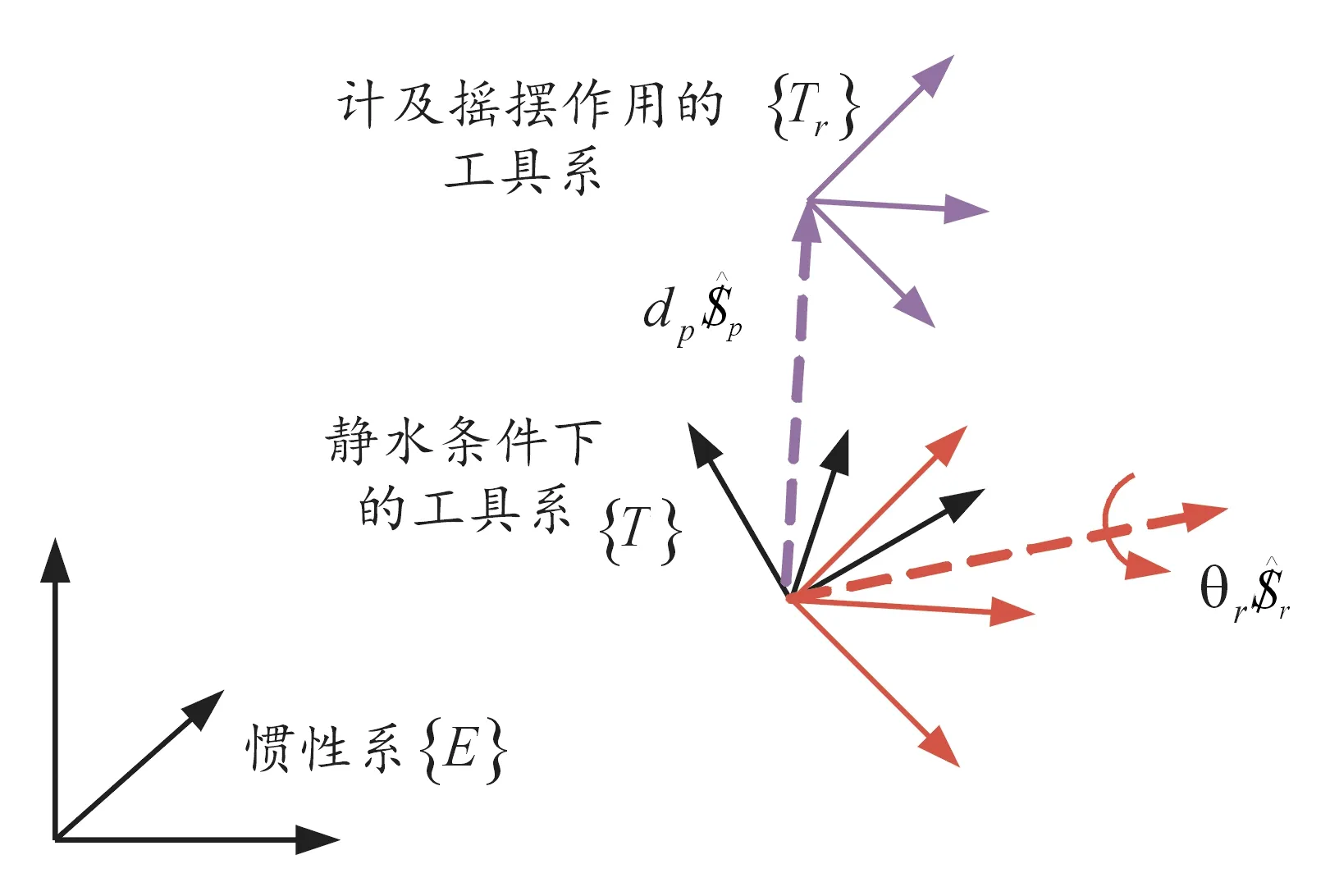
圖2 艦炮指向擾動的誤差旋量模型示意圖

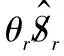
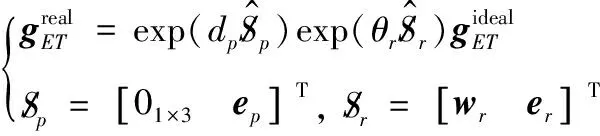
(7)

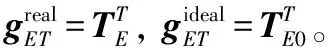
根據旋量伴隨變換定義，再將式(7)轉換為理想工具系{}中表示的誤差旋量，得出：

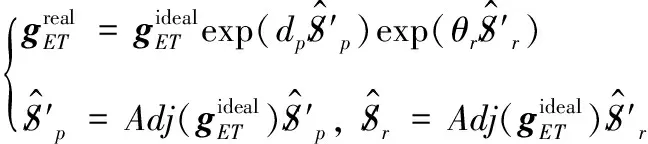
(8)

通過改寫式(8)，得出不同于式(6)擾動參數描述的炮口工具系位姿誤差為：

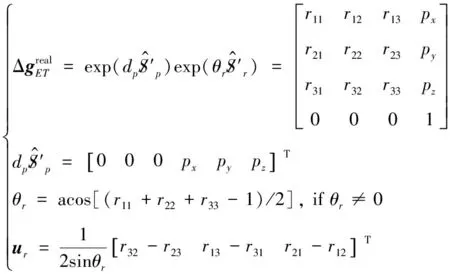
(9)

式(9)中：、、分別是炮口位置誤差在工具系描述時的軸向分量；是姿態誤差合成量；是姿態誤差旋量軸在理想工具系中的方向余弦。

3 搖擺作用下艦炮指向誤差補償模型

3.1 基于艦炮串聯運動鏈的指向誤差補償

在獲得艦炮指向誤差的基礎上，根據艦炮串聯運動鏈構造出瞄準跟蹤過程的指向補償模型為：

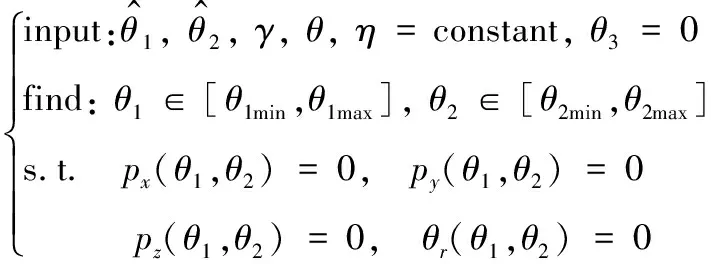
(10)

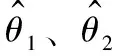
式(10)給出艦炮指向補償模型的一般表達式，包含4個約束方程、2個未知變量，誤差補償效果取決于超靜定方程組的逼近精度，解析方程在此省略。

在艦炮瞄準跟蹤時，若假設已知某目標相對慣性系{}的--歐拉角(，，)，則根據艦炮指向軸夾角與目標方位角的一致性得出：

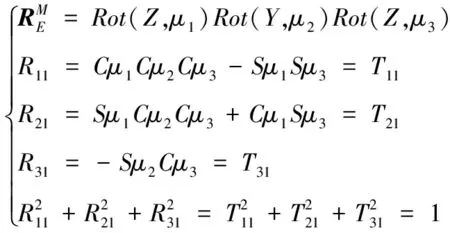
(11)

(12)

對于艦炮發射過程，雖然利用式(10)的后坐關節變量也可構造出相似的指向補償模型，但由于彈丸膛內運動時間通常小于艦炮方位和高低運動響應時間，因此很難主動控制，也無法應用于指向補償，這里不再贅述。

3.2 基于彈道解算的艦炮指向誤差補償

由于高海況下艦船搖擺運動較為嚴苛，其引起的炮口指向擾動量甚至會超越艦炮理想工作空間，因此很難對艦炮指向運動誤差進行“完全”補償。但根據大口徑艦炮彈道軌跡可以看出，即使對炮口指向進行部分補償時，也能夠實現精確打擊目標，如圖3所示。

為實現艦炮指向運動誤差的局部補償，不妨再設置補償系{}和彈丸速度系{}。并假設已知目標點在慣性系中的運動方程、彈丸在速度系中的質點彈道模型，給出射擊瞄準點的補償解算流程如下。

圖3 艦炮指向運動誤差補償模型示意圖

1) 炮口切向運動轉換。

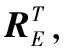
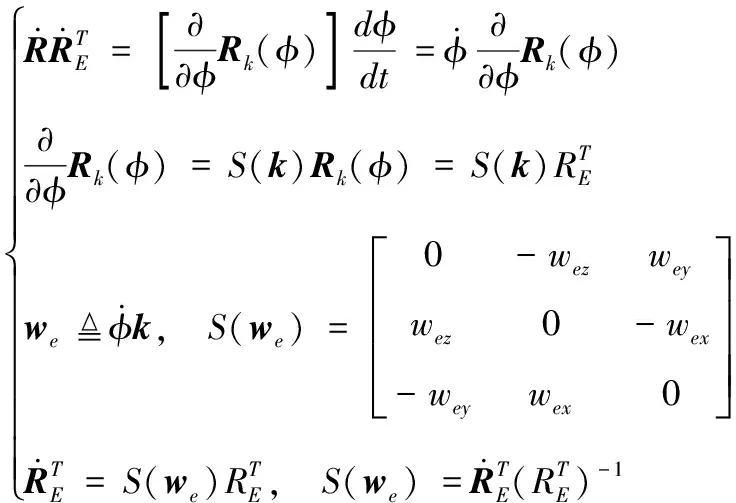
(13)

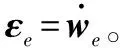
若將艦炮后坐運動轉換為工具系的位矢(沿著艦炮指向軸)，則在彈丸出炮口瞬時，根據矢量運算可推導出炮口中心點在慣性系{}中的切向運動為:

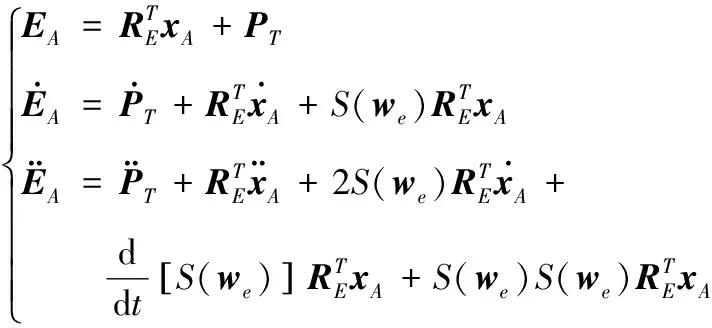
(14)

2) 坐標系齊次變換。

將待解的艦炮射擊諸元(，，)代入式(3)，得出補償系{}相對慣性系的位姿矩陣；再將彈丸出炮口瞬時的搖蕩參數、后坐位矢代入式(14)，得出炮口切向速度，，并推導速度系相對慣性系的變換矩陣為：

(15)

式(15)中：是彈丸膛內運動速度；是根據彈炮切向速度合成得出的彈丸初速，沿著速度系軸方向。

3) 彈丸質點運動轉換。

彈丸出炮口瞬時，質點位于速度系原點，時刻彈丸在速度系平面的彈道軌跡模型為：

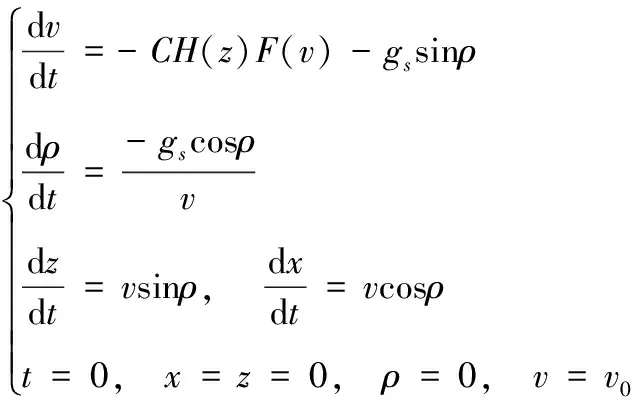
(16)

式(16)中：為重力加速度在速度系中的向分量；為彈丸速度矢量夾角；為彈道系數；為空氣密度函數；為阻力函數。數學模型詳見文獻[14-15]。

采用龍格庫塔法求解微分方程，得出彈丸飛行時的落點位置(，0，)。當式(16)改寫為彈丸的剛體彈道模型時，也可求解出更精確的落點位置。

4) 彈道命中方程。

將速度系中的彈丸落點位置轉換至慣性系，計算其與目標未來點(，，)位置的相對距離，得出艦炮修正射擊諸元下的射擊瞄準偏差Δ為：

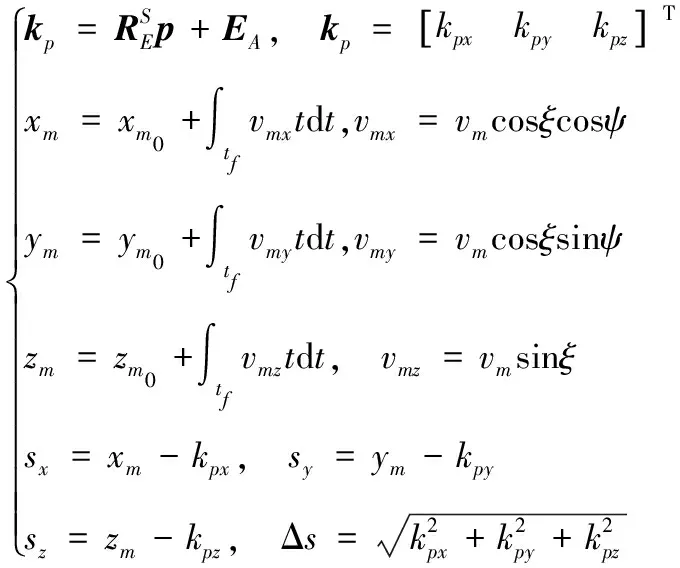
(17)

5) 艦炮修正射擊諸元優化計算。

聯立式(15)至式(17)，得出彈丸命中期望下的射擊瞄準變量優化模型為：

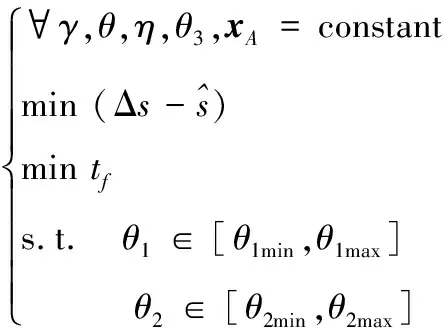
(18)

采用PLS算法或NSGA算法對式(18)的多目標優化模型進行求解，得出的Pareto最優解集，即能對艦炮指向誤差進行局部補償，從而實現精確打擊的目標。

4 仿真驗證

4.1 艦炮指向運動誤差分析

以某艦船裝載的大口徑艦炮為對象，假定高海況下艦船搖擺譜參數、艦炮零位對準時的結構矢量、方位角和高低角范圍、后坐運動/彈丸膛內運動參數等分別為：

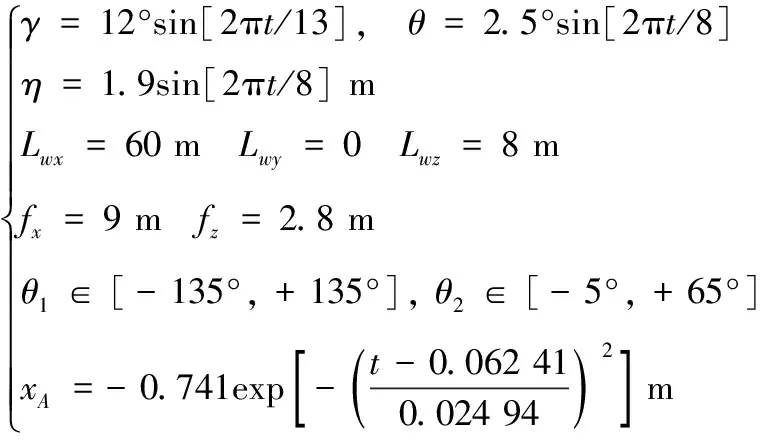
對于艦炮瞄準跟蹤過程，設置方位驅動在6 s內由零位調轉至120°，高低驅動在2 s內由零位調轉60°，后坐驅動保持為零值。根據式(6)得出慣性系中描述的艦炮原點軌跡誤差和指向誤差不再展示，根據式(9)得出工具系描述的艦炮指向誤差如圖4所示，包絡最值是各點軌跡(搖擺參數組合確定)下的最大值和最小值。

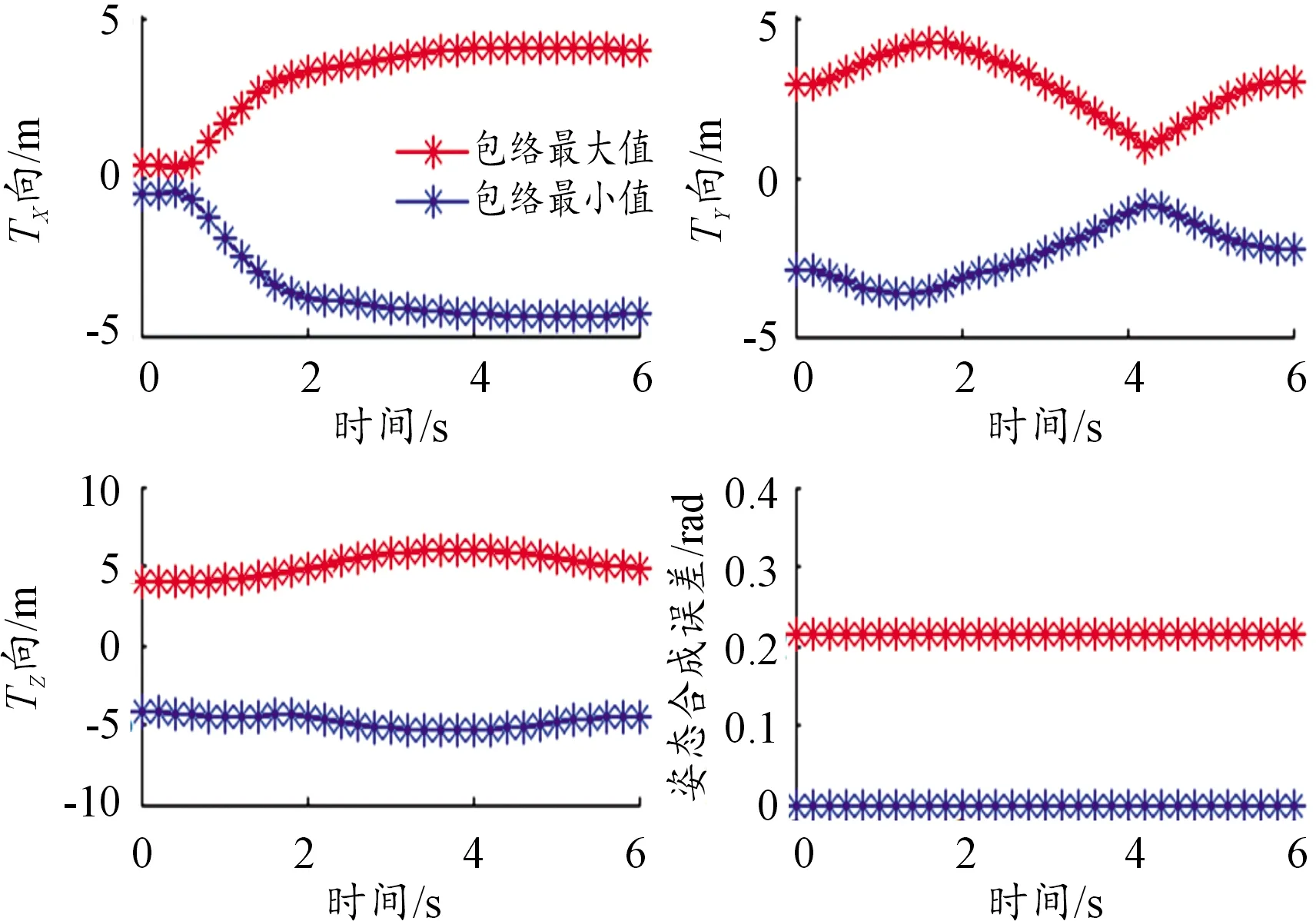
圖4 搖擺作用下炮口軌跡誤差和指向誤差曲線

由圖4可以看出：艦船搖擺運動作用于艦炮串聯運動鏈的虛擬連桿副，其引起的疊加擾動域導致炮口絕對軌跡出現了較大的偏移；所建指向誤差模型能夠準確預測艦炮的最大可能擾動域，明確搖擺作用下艦炮指令信號響應。

4.2 艦炮指向誤差補償分析

在明確艦炮指向誤差之后，采用PLS算法對超靜定方程組進行數值逼近，圖5給出了采用全約束解的艦炮指向補償效果。其中理想方位角0°、高低角60°，橫軸是橫縱搖和垂蕩運動參數的獨立組合。

由圖5可以看出：通過求解超靜定方程組得出艦炮關節運動變量時，姿態誤差角零值的前置條件是++=3，即需滿足姿態誤差矩陣為單位陣的隱含約束；但由于艦炮不具有橫縱搖和垂蕩方向的自由度，因此從串聯系統的角度搖蕩運動引起的艦炮指向誤差無法完全補償；在不同的搖蕩組合參數下：① 姿態誤差和向誤差逼近零值，其余兩向位置殘余誤差相比無補償值減小約40，② 若位置誤差都逼近零值時，姿態殘余誤差減小約67，相對實際炮口指向，位姿補償效果總體接近34左右。

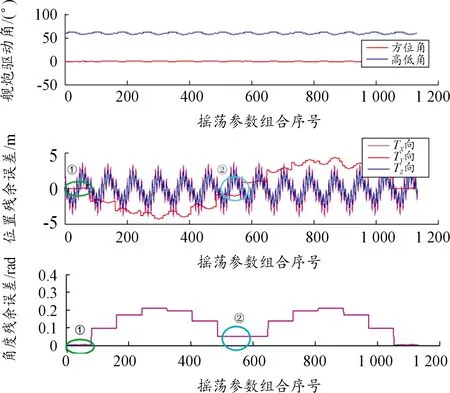
圖5 基于艦炮串聯運動鏈的指向誤差補償效果曲線

若假定目標方位角(-60°，30°，30°)時，根據指向一致性得出不同搖蕩參數組合條件下，艦炮方位和高低角如圖6所示。由圖6可以看出：解析模型能夠獲得與搖蕩參數對應的精確值，炮口姿態補償效果可達到100%。

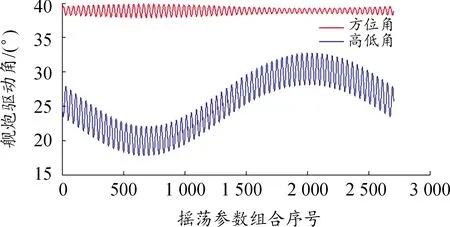
圖6 艦炮指向目標方位補償曲線

假設彈丸質點運動按照標準氣象彈道條件，根據艦船搖擺參數、方位驅動(-6°，6°)、高低驅動(25°，55°)以及后坐運動30 ms的條件，彈丸初速850 m/s、飛行時間60 s，設置某目標未來點在慣性系中的坐標(25，0，0)km、彈著散布半徑為30 m時，根據射擊瞄準點的補償解算流程得出彈道軌跡如圖7所示。其中，可行概率表示指定射擊諸元下滿足精度要求的搖擺條件。

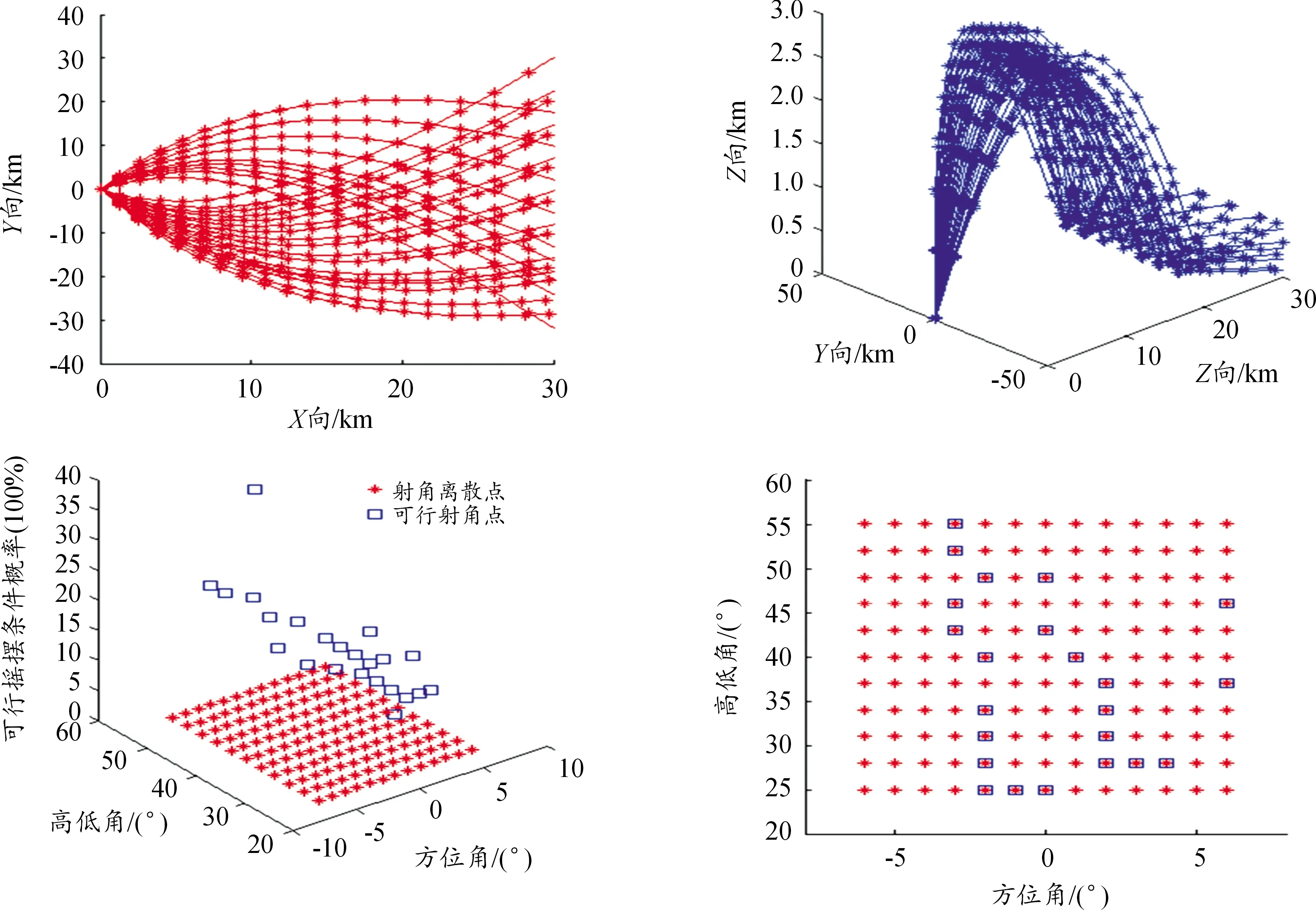
圖7 艦炮射擊瞄準解算的彈道軌跡圖

由圖7可以看出：彈丸飛行時間越長(以落點至水平面為截止時間)，艦船搖擺對彈丸飛行軌跡的影響越大，在搖蕩參數組合條件下，同組射擊諸元的彈丸落點范圍較大；對于指定目標點，雖能夠得出23組修正射擊諸元，但可行搖擺條件概率最大僅為40%，表明該射擊諸元下預設的10組搖擺組合參數中僅有4組能夠滿足彈著點要求；通過與143組彈道軌跡數目比對，炮口指向局部補償效果約為16%左右，當搖擺運動較為劇烈時，射擊瞄準補償的無解情形更多。

5 結論

為保障艦炮射擊諸元求解精度，根據艦炮多體系統串聯運動鏈建立了搖擺作用下的指向誤差模型，根據機構運動精度及彈道方程分別構造了艦炮指向補償模型，并對搖擺補償解算流程進行仿真驗證。仿真結果表明：指向誤差模型能夠描述搖擺作用下艦炮瞄準跟蹤、定點及跟蹤射擊時的炮口最大擾動域；對于搖擺補償，艦炮串聯系統不具備與搖蕩運動關節對應的“主動”自由度，艦船搖擺引起的指向擾動屬于不可完全補償誤差，位姿補償總體效果約為34%；通過目標方位一致性或解彈道方程對指向誤差進行局部補償，計及炮口非慣性系中的彈丸初始擾動和累積效應，射擊瞄準補償效果約為16%，可以獲得滿足落點彈丸偏差裕度要求的艦炮射擊諸元，實現搖擺條件下的艦炮精確打擊功能。