考慮焊料空洞損傷的IGBT雙向熱網絡模型

蔡彥閣，杜明星，姚婉榮

（1.天津理工大學 天津市復雜系統控制理論及應用重點實驗室，天津 300384；2.天津中科華盈科技有限公司，天津 300300）

0 引言

近年來，電力電子裝置在電動汽車、風力發電、航空航天等領域廣泛應用。而功率器件作為電力電子裝置的核心[1]，由于長時間工作在高溫環境中，其可靠性受到了一定的制約。因此，提高功率器件的可靠性是決定系統能否穩定運行的關鍵。IGBT 模塊的封裝級失效類型主要有鍵合線失效和焊料層失效，而焊料層失效主要是由于焊料層中出現空洞和裂紋損傷所致。在模塊封裝過程中，當空氣中的氣泡嵌入環氧材料就會在焊料層產生空洞[2]。盡管新的焊料工藝可以有效地限制焊料層空洞產生，但不能完全消除它[3]。在IGBT 模塊工作中，焊料層承受熱應力也會產生空洞損傷。

Bladimir 等人研究了焊料層中實際空洞率與導熱系數關系，并將空洞對焊料層溫度產生的影響進行評估[4]。陳民鈾等人提出了計及焊料層疲勞的IGBT 模塊壽命評估，研究高頻下芯片焊料層與DBC 焊料層分別出現老化時對結溫的影響[5]。文獻[6]通過有限元仿真，研究去除硅膠和外殼的IGBT 模塊在出現空洞損傷時芯片結溫分布，并建立了考慮空洞損傷的Cauer 模型。焊料層損傷會減小熱流路徑，使更多熱流集中在空洞附近，降低IGBT 模塊的散熱性能，導致結溫升高，進而加快模塊的老化過程。故研究焊料層空洞對IGBT 芯片溫度分布的影響，以及準確監測老化后IGBT 模塊的結溫具有重要意義。然而，熱量在模塊內部傳遞時受其物理結構的影響[7]，硅膠和外殼是模塊的重要組成部分，會對熱流傳遞產生影響。很多研究成果僅僅專注于芯片及其下層結構對熱流傳遞的影響[5-7]，導致熱仿真模型和熱網絡模型與實際模塊結構不相符，然而考慮硅膠和外殼的模型更為真實。因此，本文研究當焊料層出現空洞損傷時，硅膠和外殼對IGBT 芯片溫度的影響。

1 IGBT模塊的熱模型

本文以型號為WGL100B65F23 的模塊作為研究對象，表1 是各層狀結構的尺寸，表2 是各層材料的參數。

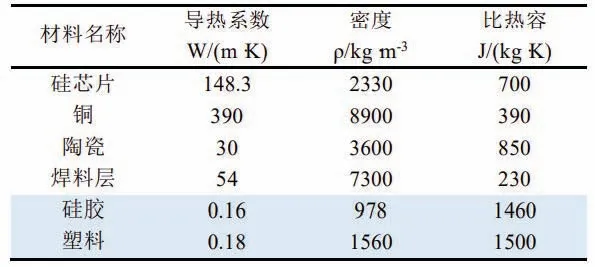
表2 IGBT模塊各層材料的參數Table 2 Material parameters of each layer of IGBT module

為研究芯片焊料層空洞對結溫的影響，選取定制的焊料層空洞率為5.5%、9.4%和15%的模塊作為研究對象，圖1 是其芯片焊料層的X 光照片。

圖1 芯片焊料層空洞分布圖Fig.1 Void distribution map of chip solder layer

1.1 傳統模型

傳統Cauer 模型忽略了硅膠和外殼對溫度的影響，只包括芯片及其下層結構。每一層結構用一對熱阻和熱容來表示。

由于空洞中充滿空氣或為真空狀態，當芯片焊料層出現空洞時，其熱阻值增大，熱容值減小，散熱性能下降，導致模塊結溫升高。為計算芯片焊料層出現空洞后的準確結溫，需建立考慮空洞損傷的Cauer 模型。

圖2 所示為健康模塊和老化模塊的有效傳熱區域示意圖。為清楚表示空洞對有效傳熱面積的影響，假設焊料層出現了一個面積較大的空洞，將焊料層分成左右兩部分。由于空洞的傳熱能力遠小于焊料，可以將空洞近似為絕熱。由空洞隔開的兩部分焊料層對于其下層結構來說是兩個鄰近的熱源，熱量向下傳播時有效傳熱面積以一定的角度擴大，兩部分焊料層的有效傳熱區域出現耦合。交叉部分的溫度高于其他有效傳熱區域，因此在空洞上方的芯片處出現高溫區域。

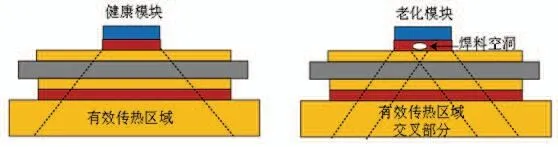
圖2 健康和老化模塊的有效傳熱區域對比Fig.2 Comparison of effective heat transfer area of healthy and aging modules

本文主要研究焊料層出現空洞時的情況，因此在建立仿真模型時忽略鍵合線以及接線端子的影響。在有限元仿真過程中，將模塊底部的溫度設置為室溫，通過設置邊界條件來模擬散熱器，假設續流二極管不發熱，通過在IGBT芯片上施加功率損耗來模擬模塊工作時芯片的產熱，根據表2 所給的數據設置模塊各層狀結構的參數。

健康和出現空洞損傷的模塊中未考慮硅膠和外殼的有限元仿真模型的芯片溫度分布，如圖3 所示。健康模塊的芯片的中央位置溫度最高，向四周呈遞減趨勢，中心到邊緣的溫度梯度較小，紅色的高溫區域較大，溫度分布均勻。當芯片焊料層出現空洞時，隨著空洞率的升高，芯片的最高溫度增大。芯片的最高溫度由芯片中央轉移到空洞集中或較大面積空洞的上方，芯片的高溫區域減小，中心到邊緣的溫度梯度增大。仿真結果與上文的理論分析一致。

圖3 未考慮硅膠和外殼的仿真模型的芯片溫度分布Fig.3 The chip temperature distribution of the simulation model without considering the silicone and shell

傳統熱網絡模型在計算熱阻和熱容時，并未考慮有效傳熱區域的耦合現象。健康模塊的熱量分布均勻，用這種方法計算有效傳熱面積時不會產生較大誤差。當芯片焊料層出現空洞時，這種計算方法會使熱阻熱容值與實際情況相差較大，進而使熱網絡模型計算的結溫出現較大誤差。但由于空洞位置和大小的隨機性，很難實現在實際工況中考慮空洞對有效傳熱區域的影響。而經過熱仿真發現，硅膠和外殼可以使結溫分布均勻，在建立熱網絡模型時可忽略空洞對有效傳熱區域的影響。因此，本文建立考慮硅膠和外殼的雙向熱網絡模型，以逼近實際的物理工況。

1.2 雙向熱網絡模型

焊料層出現空洞時，考慮硅膠和外殼的熱網絡模型如圖4 所示。由于此模型同時考慮了芯片的上、下層結構，因而稱之為雙向Cauer 模型。基于傳統Cauer 模型的原理，分別用一對RC 來表示硅膠和外殼的熱阻和熱容，其數值見表3。

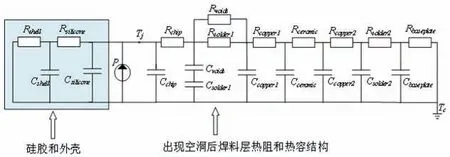
圖4 考慮空洞損傷的雙向Cauer模型Fig.4 Bidirectional Cauer model considering void damage

表3 熱網絡模型的RC參數Table 3 RC parameters of the thermal network model

圖5 是考慮硅膠和外殼的IGBT 模塊的有限元分析模型，圖6 為考慮硅膠和外殼的仿真模型的芯片溫度分布。健康模塊的芯片溫度分布與不考慮硅膠和外殼時的芯片溫度分布接近。而當焊料層出現空洞時，硅膠和外殼可以減小芯片溫度分布受空洞的影響，最高溫度更接近芯片的中央位置，較大面積的空洞上方位置的溫度均勻，芯片高溫區域較大，溫度梯度較小。由于芯片溫度分布均勻，在計算熱網絡模型的熱阻和熱容時，可忽略空洞對有效傳熱面積的影響。

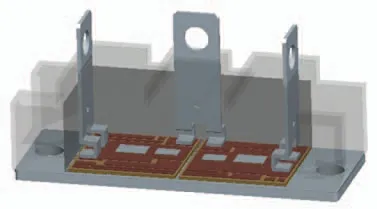
圖5 考慮硅膠和外殼的有限元仿真模型Fig.5 Finite element simulation model considering silicone and shell

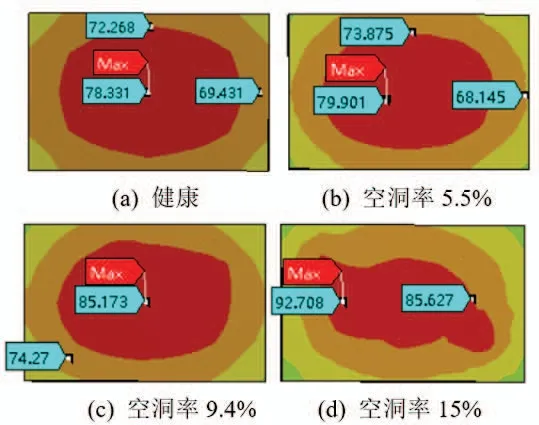
圖6 考慮硅膠和外殼的仿真模型的芯片溫度分布Fig.6 The chip temperature distribution of the simulation model considering the silicone and shell

1.3 硅膠和外殼對結溫的影響

熱網絡模型中的熱容在穩態時相當于開路，此時雙向Cauer 模型相當于硅膠和外殼的熱阻之和（記為R1）與其余7 層結構的熱阻之和（記為R2）并聯，由于R1遠大于R2，雙向Cauer 模型的穩態結溫與傳統模型接近。而當芯片焊料層產生空洞后，R2增加，但R1仍然遠大于R2，所以兩種模型的穩態結溫相差較小。在暫態過程中，由于硅膠的熱容值較大，雙向模型的結溫上升較慢，使結溫達到穩態的時間增大。因此，硅膠和外殼對穩態結溫影響較小，對暫態結溫影響明顯。

圖7(a)所示是空洞率為15%的模塊的兩種模型在有限元熱仿真中的結溫上升過程，在達到穩態時兩種模型的結溫差僅0.3℃左右，但在暫態過程中，考慮硅膠和外殼的模型的結溫上升較慢，兩模型的結溫差較大。仿真結果與Cauer 模型的分析一致。

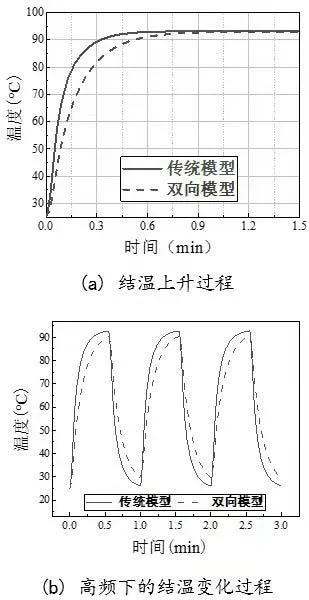
圖7 結溫變化圖Fig.7 Diagram of junction temperature changing

影響IGBT 模塊壽命的關鍵參數除了最大結溫外，還有結溫波動ΔTj。若模塊工作于高頻下，芯片導通的時間（即產生功率損耗的時間）小于結溫達到穩態所需的時間，此時硅膠和外殼對暫態結溫的影響更加明顯，甚至會減小達到動態平衡后的結溫。圖7(b)是高頻下，空洞率為15%的模塊的兩種模型在熱仿真中的結溫上升過程。在結溫達到動態平衡后，單向模型的最大結溫為92.735℃，結溫波動為66.683℃，而雙向模型的最大結溫為90.653℃，結溫波動為61.335℃。雙向熱網絡模型的最大結溫和結溫波動均小于單向熱網絡模型。

硅膠和外殼能有效減小高頻下模塊的最大結溫和溫度波動，而在實際應用中，IGBT 模塊通常處于高頻工況下。因此，硅膠和外殼不僅使芯片溫度分布均勻，還提高了模塊的可靠性。

2 實驗分析與驗證

2.1 實驗平臺

為驗證雙向Cauer 模型分析的正確性，本文通過實驗獲取IGBT 模塊的結溫。采用紅外成像儀、熱電偶等設備直接測取模塊結溫時，需要打開模塊的封裝結構，這種實驗方法無法獲取完整封裝的模塊的結溫。因此，本文通過熱敏電參數與結溫的關系推算結溫。其中，通態壓降Vce是最常用的熱敏電參數。

搭建圖8 所示的實驗平臺。在實驗過程中將IGBT 模塊放置在加熱板的中央位置，設置加熱板的工作溫度為25℃～125℃，步長為25℃，使模塊充分受熱，此時可以認為加熱板的溫度與結溫Tj相等。設置集電極電流為1A～40A，步長為2A，記錄不同集電極電流下Vce的值，獲得到不同溫度下的I-V 特性曲線。根據I-V 特性曲線擬合得到圖9 所示的Tj與Vce和Ic的關系曲面。

圖8 實驗平臺Fig.8 The experiment platform

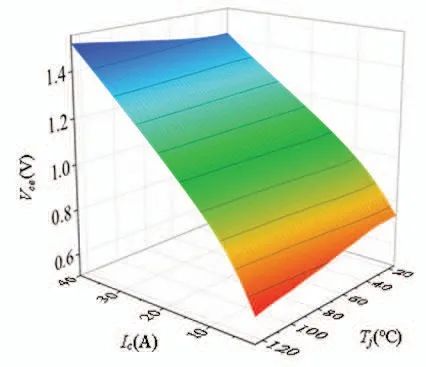
圖9 Tj與Vce和Ic的關系曲面Fig.9 The relation surface of Tj to Vce and Ic

2.2 實驗結果

通過以上實驗步驟，獲得健康的模塊和空洞率分別為5.5%、9.4%、15%的模塊的Tj與Vce和Ic的關系曲面。在室溫下，分別給上述模塊的集電極通入恒定電流，記錄模塊達到穩態前不同時刻的通態壓降和結溫。將通態壓降與集電極電流的乘積作為芯片的功率損耗輸入熱網絡模型，通過計算獲取模塊的結溫。圖10 為雙向Cauer 模型計算的結溫與實驗測量結溫對比，由于空洞率為5.5%的模塊的結溫與健康模塊結溫接近，只繪制了健康模塊以及空洞率為9.4%、15%的模塊的結溫曲線。兩種方法獲得的結果吻合度高，證明雙向Cauer 模型的準確性。

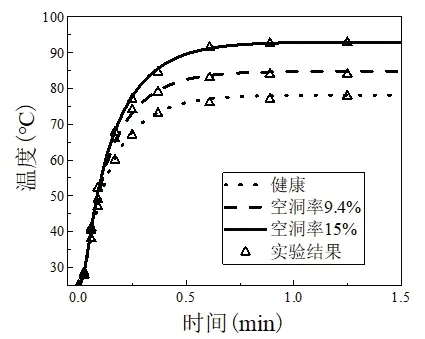
圖10 雙向Cauer模型計算的結溫與實驗對比圖Fig.10 Junction temperature calculated by bidirectional Cauer model and experimental comparison diagram

3 結論

本文基于IGBT 模塊的硅膠和外殼對結溫的影響，提出了一種雙向熱網絡模型，解決了當芯片焊料層出現空洞后熱網絡參數較難確定以及熱網絡模型計算的結溫不準確的問題。通過有限元分析發現，當芯片焊料層出現空洞時，硅膠和外殼可以減小芯片最高溫度位置的偏移，降低空洞上方位置的溫度，使芯片高溫區域周圍的溫度梯度減小，溫度分布更接近健康模型，進而可以簡化熱網絡模型參數的提取。而當模塊工作于高頻時，硅膠和外殼可降低模塊的溫度波動，進而減小模塊達到動態平衡后的結溫，對IGBT 模塊起到重要的保護作用。本文通過仿真和實驗驗證了利用該模型提取IGBT 模塊結溫的可行性和準確性，有利于電力電子器件可靠性的檢測。