基于ALSTM的光伏出力短期預測研究

韓 坤

（中國大唐集團科學技術研究總院有限公司，北京 100040）

0 引言

隨著全球對環境問題的關注，開發諸如風能[1]、水能[2]、燃料電池[3]、光伏[4]等可再生能源已成為普遍共識。國際能源署（International Energy Agency，IEA）評估，到2040 年，新能源的比例將達到60%，其中光伏和風能將占50%以上。光伏，即太陽能光伏，自1992 年以來，已從小規模應用的利基市場發展成為主流電源。2017 年，全球累計光伏發電量達到近460TWh，約占全球總能源的2%，其中60%用于公用事業的應用，其余40%用于分布式應用[5]。到2018 年底，全球累計光伏總容量達到512 千瓦，滿足了全球2.55%的電力需求[6]。

但是，由于環境溫度、相對濕度、風速和晴空指數等氣象因素[7]，光伏發電具備間歇性的特性，會有相當大的波動性。在文獻[8]中使用了神經網絡來驗證光伏功率輸出與溫度、風速和相對濕度密切相關性，文獻[9]則證明了晴空指數和溫度對光伏功率輸出的性能有很大的影響。由于光伏發電輸出受氣象因素影響很大，強波動和間歇性會對電力系統運行和并網造成很大影響。當光伏大規模并網時，可能會引起電網振蕩[10]。因此，準確預測光伏出力可以顯著改善電力系統的運行，增加光伏系統的滲透率。

光伏功率預測的方法可概括為物理方法、直接預測方法和間接預測方法。物理方法主要依賴于從太陽能到電能的能量轉換的理論分析獲得的物理模型，物理模型通常基于數值天氣預報、衛星圖像和云運動模型[11]，這些模型可以高精度地預測光伏功率輸出[12]。但是，這種預測方法需要衛星云圖上的額外信息，導致更高的運行成本和計算成本。為解決此問題，直接預測方法，即時間序列方法被廣泛應用于光伏預測。這些方法根據光伏功率序列的周期性、趨勢性和其他特性，在歷史功率序列和未來光伏功率之間建立數學關系。但是，這種方法缺少輻射、溫度、濕度、風速和風向等氣象信息，不完整的天氣信息難以保證預測的準確性。為了提高預測精度，提出了間接預測方法，即回歸方法。考慮氣象因素后，某一時段光伏發電量的預測性能有了顯著提高。間接預測方法包括人工神經網絡[13,14]、支持向量機[15]和馬爾可夫鏈[16]等。

本文通過深度學習方法，在基于MIE 構建的光伏特征輸入基礎上，利用ALSTM 的預測優勢，采用回歸方法對光伏出力進行了較為準確的短期預測。

1 ALSTM深度網絡

1.1 長短期記憶網絡（LSTM）

LSTM 是目前機器學習領域中廣泛使用的深度學習方 法，由Hochreiter 和Schmidhuber 在1997 年 提出[17]。LSTM 是專門用于處理時間序列數據的深度學習模型，其在網絡模型中加入門控制器，可以解決RNN 中的長期依賴問題（梯度爆炸或消失），結構如圖1 所示。

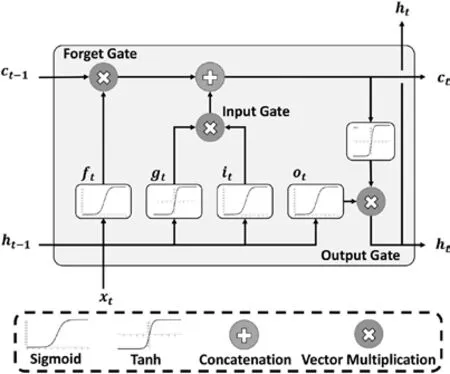
圖1 LSTM網絡結構Fig.1 LSTM Network structure

LSTM 模型在原有的短期記憶單元ht的基礎上，增加一個記憶單元ct來保持長期記憶，同時增加3 個門控機制來控制整個學習過程中的信息流。LSTM 單元在每個時間步長t的狀態被定義為一組5 個向量Rd：輸入門it、遺忘門ft、輸出門ot、隱藏狀態ht和存儲單元ct，d是LSTM 單位的數量。LSTM 傳遞函數為：

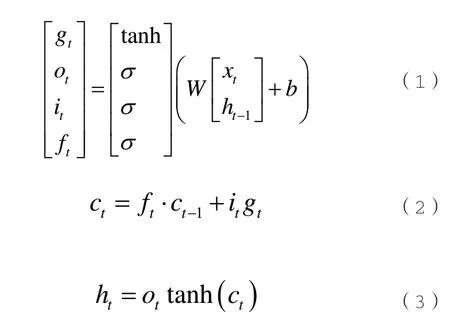
其中，xt是當前輸入；σ表示sigmoid 函數；W和b是權重和偏置參數。遺忘門控制從存儲單元刪除不需要的信息，而輸入門控制向存儲單元添加新信息，輸出門控制內部存儲狀態的暴露。通過3 個門，存儲單元ct可以選擇性地更新、刪除和遺忘內部信息，從而更好地理解序列中的長期依賴性，提取時序數據中隱藏的特征。

1.2 注意力機制（Attention）

當神經網絡接收到大量的輸入信息輸入時，不同的輸入對輸出值的影響是不同的。為提高神經網絡的計算效率，對于相同的輸出，更多的計算能力被分配給重要的輸入信息，這種措施被稱為注意力機制。

注意力機制分兩步計算，第一步是計算所有輸入值上的注意力分布值αi；第二步是計算單個輸出值下的輸入信息加權平均值。注意力機制如圖2 所示。

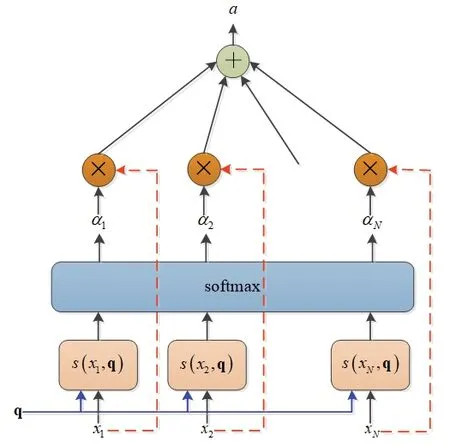
圖2 注意力機制結構圖Fig.2 Structure diagram of attention mechanism

其中，xi是輸入值；q是神經網絡的查詢向量；s是注意力的得分函數；αi是查詢向量q在所有輸入值上的注意力分布值。

得分函數為：

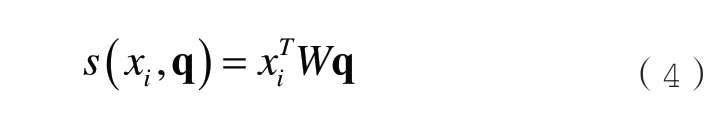
其中，W是可以自主學習的神經網絡參數。計算式（4）的softmax 值，可以得到注意力分布αi，如式（5）所示：

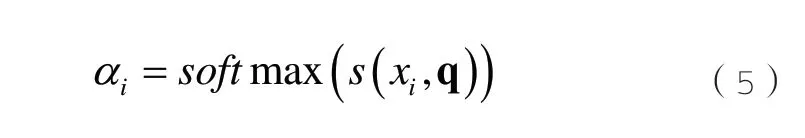
a是注意力分布值α和輸入值xi的加權平均值，表示為：

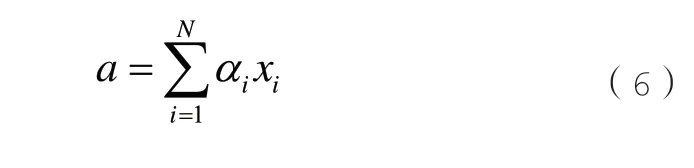
2 基于ALSTM的光伏短期功率預測

2.1 基于互信息熵(MIE)的相關性衡量

互信息為信息論中用來度量變量間信息共享程度的方式，它可以表征一個隨機變量與另一個隨機變量信息的相關性情況[18,19]。

定義向量X=[x1，x2，，，xn]，n為X的長度。如式（7）所示對X進行歸一化計算：

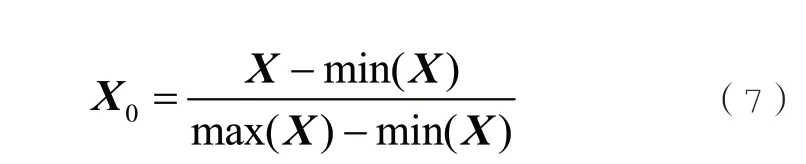
式（7）中，X0是X歸一化處理后的結果。

設B為X0的組距，Ei為X0的波動區間上下限，其計算公式分別如式（8）和式（9）所示：

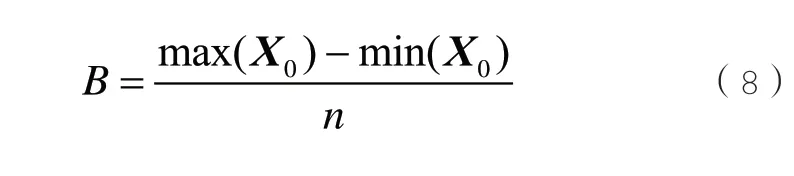
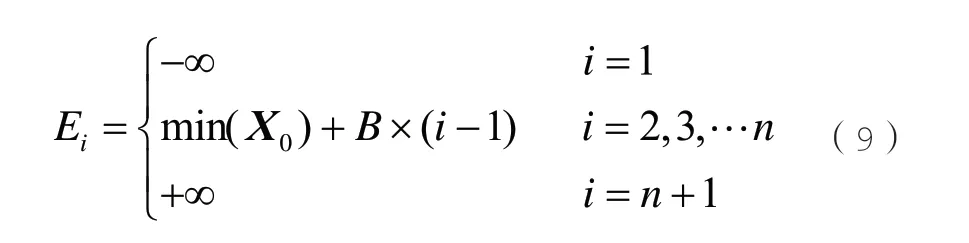
依據一維直方圖分析法，按式（9）將X0分為n個波動區間，設Xi表示第i個波動區間，如式（10）所示：

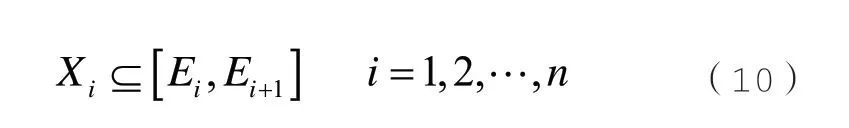
設p(·)表示上下限概率密度函數，則各波動區間Xi的上下限概率密度p(Xi)為：

式（11）中，ni為X0中元素在波動區間Xi的數據樣本數。

通過自信息熵H(Xi)來表征X自身隨機波動的不確定度大小，即：

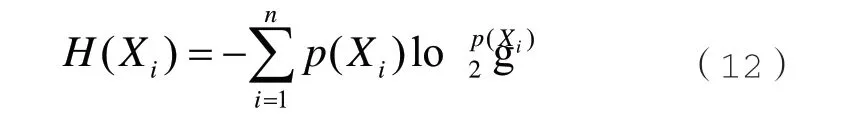
依據香農信息論[15]，一維向量的自信息熵H(Xi)擴展到二維向量的互信息I(X;Y)，即為：

式（13）中，Y為與X不同的向量；p(Yj)為波動區間Yj的上下限概率密度；p(XiYj)表示X0和Y0在波動區間Xi和Yj的聯合概率密度。

I(X;Y)表征了X和Y信息的共享程度，可用于衡量兩個變量中一個同另一個相關性的大小情況。若向量X和向量Y彼此獨立無關，那么向量X將不會給向量Y提供任何信息，它們彼此間的互信息為零；反之，若向量X和向量Y互相相關，則X和Y之間所傳遞的全部信息都會共享，那么二者間的互信息I(X;Y)=1。

為消除量綱的影響，廣義互信息I(X;Y)經過歸一化計算后，最終得MIE 相關系數IXY為：

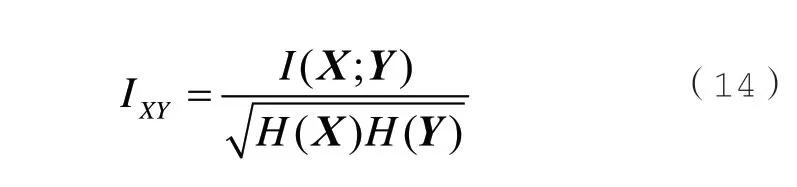
式（14）中，H(Y)表示向量Y的自信息熵。

MIE 表征了變量之間概率分布的統計特性，其始終是非負的，即IXY≥0，與廣義的線性相關系數相關，可應用的范圍更廣，能更好地挖掘氣象因素與光伏功率間的非線性相關性，有利于關鍵氣象特征的篩選。

2.2 光伏特征輸入選取

通過維度較大的數值天氣預報（uNmerical Weather Forecast，NWP）氣象數據進行光伏功率預測之前，要先對復雜氣象輸入數據與光伏功率輸出數據進行關聯性分析。要將與光伏功率相關性低的變量進行剔除，也即減少預測模型的噪聲輸入，對輸入氣象數據降維，提高預測模型精度的同時，也提升預測模型的運行效率。

若各氣象變量Xi(i=1，2，…，5)分別為輻照度、溫度、云量、風速和濕度，光伏功率則以變量Y表示。通過利用2.1 小節公式分別計算各輸入氣象因素與輸出光伏功率的互信息熵（MIE）相關系數IXY=[IFP，ITP，ICP，IWP，IHP]，其計算結果見表1。

表1 氣象因素和光伏功率的MIE相關系數Table 1 MIE correlation coefficients between meteorological factors and photovoltaic power

從表1 可知，各氣象因素與光伏功率的MIE 相關系數由大到小分別是照度、溫度、濕度、風速和云量，即輻照度和溫度與光伏功率相關性最高，均大于0.9。為了最大程度地平衡訓練精度和訓練效率的關系，本文最終將MIE相關系數較高的前3 種氣象因素，輻照度、溫度及濕度作為光伏功率ALSTM 預測模型最終的輸入變量，同時前一時刻光伏功率與當前時刻功率亦是強相關的，因此本文也將前一時刻的光伏功率送入預測模型。

2.3 預測誤差指標

好的預測誤差指標有助于預測模型更好的迭代尋優，也可方便進行不同算法之間的對比，本文選取常見的均方根誤差和平均絕對誤差作為預測誤差指標，具體定義如下：

1）均方根誤差

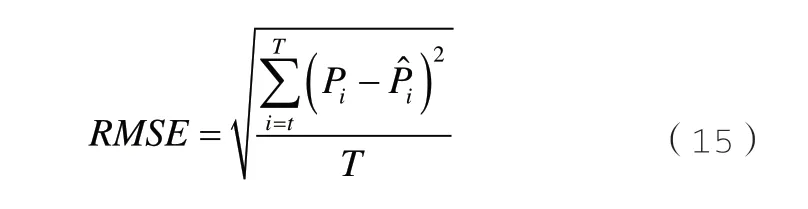
2）平均絕對誤差

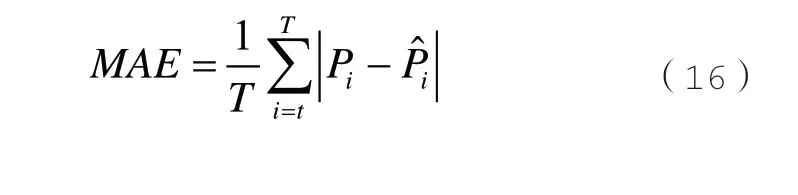
式中：T為的采樣時間點數；Pi和分別代表i時刻實際值和預測功率值。

3 仿真驗證

3.1 數據集

本文數據集取自澳大利亞布里斯班昆士蘭大學露西亞校區的平板光伏系統的昆士蘭大學中心（UQ Centre），該樓布置在建筑物屋頂的1806 塊多晶硅太陽能電池構成，裝機容量為433.44 kW[20]，如圖3 所示。原始數據集是2012 年～2013 年完整的2a一 每天24h 和1min 采樣周期的數據一因為光伏功率具有間歇性的特性，所以本文數據集實際只提取每天07:00～18:00 時間段的功率數據，從而原始的功率數據集包括481800 個采樣點的數據（2a×365d×11h×60min），其中缺失了5034 個數據，占總數據的百分之一左右，本文通過向前平均法進行缺失數據的填充處理。

圖3 昆士蘭大學中心（UQ Centre）光伏系統Fig.3 University of Queensland Center (UQ Centre) photovoltaic system

為了平衡數據量和數據自身特征的保留情況，本文對原1min 采樣周期的原始數據進行了重采樣，每15min 提取一個數據，遇到缺失數據，則通過向前15 個數據平均替代，使預測時間尺度由1min 調整為15min，最終的光伏功率數據點總數為32320（15min）。

3.2 預測效果

為了驗證本文所提ALSTM 預測模型的有效性和優越性，本文在昆士蘭大學中心光伏數據集上，分別進行了晴天功率預測、陰雨功率預測以及天氣劇烈波動日預測，同時還將雙向LSTM（BiLSTM）和卷積神經網絡（CNN）進行對比驗證。

◇晴天數據預測

以2013 年6 月某天晴為預測數據樣本，通過ALSTM預測模型進行預測。預測曲線如圖4 所示。從圖4 可知，晴天天氣條件下，總體的光伏功率波動均較小，由表2 的RMSE 和MAE 預測誤差指標值可知，ALSLTM 比BiLSTM和CNN 的預測誤差更小。

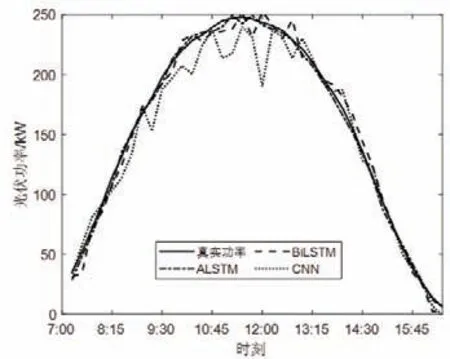
圖4 天晴日光伏功率確定性預測Fig.4 Deterministic prediction of photovoltaic power on sunny days

表2 光伏功率預測對比Table 2 Comparison of photovoltaic power predictions

◇陰雨天數據預測

為驗證本文提出的ALSTM 預測模型在其他氣象條件下的預測精度情況，選取6 月某一陰雨天作為光伏功率預測數據樣本進行預測。預測結果如圖5 所示。從圖5 可知，陰雨天氣下，光伏功率相比晴天整體波動要大。從表2 的兩個誤差指標可知，與另外兩種深度學習算法預測結果相比，本文方法預測精度更高。

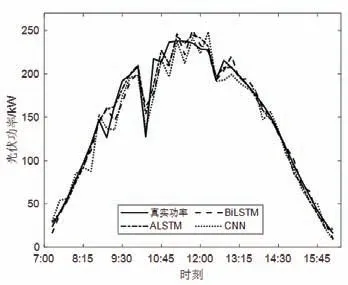
圖5 陰雨天光伏功率確定性預測Fig.5 Deterministic prediction of photovoltaic power in cloudy and rainy days

◇復雜強波動天氣數據預測

一個預測模型的好壞取決于其可否很好地在惡劣天氣情況下，進行光伏功率預測。為驗證本文提出ALSTM 在復雜強波動天氣下的光伏功率預測情況，選取6 月某一強波動數據樣本進行功率預測，預測結果如圖6 所示。結合圖6 以及表2 兩個預測誤差指標可知，復雜強波動天氣下的光伏功率波動比陰雨天更大，但ALSTM 預測誤差相對較小。與另外兩種方法相比，精度更高，能更好地進行光伏功率預測，體現了本文ALSTM 預測模型的優越性和強魯棒性。

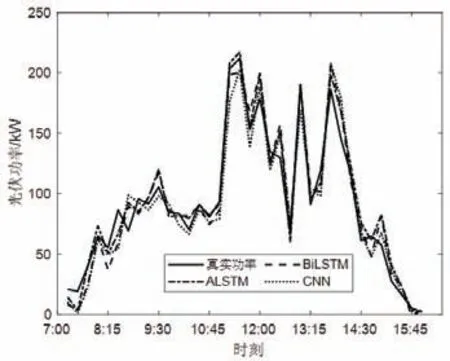
圖6 天氣劇烈變化日光伏功率確定性預測Fig.6 Deterministic prediction of photovoltaic power on days with severe weather changes

4 結論

準確可靠的光伏出力預測對改善電力系統運行能起到很大作用。本文基于LSTM 提取時序數據關聯特征的優勢，以注意力機制進一步改善LSTM 網絡，構建了ALSTM 預測模型，通過MIE 方法衍生光伏特征輸入，對影響光伏功率預測的復雜氣象因素進行降維處理，進一步減少輸入噪聲和提示預測精度。在昆士蘭大學中心光伏出力數據上，通過天晴、陰雨天以及天氣劇烈波動日的光伏功率預測情況，并與BiLSTM 和CNN 的對比驗證可知，ALSTM 能更準確地在晴天、陰雨天以及天氣劇烈波動日等情況下進行光伏出力預測，具有更好的魯棒性和適用性。