基于非下采樣剪切波變換—參數自適應脈沖耦合神經網絡的屬性融合裂縫預測方法

湯 韋 李景葉* 王建花 薄 昕 耿偉恒 葉 瑋

(①中國石油大學(北京)地球物理學院，北京 102249； ②油氣資源與探測國家重點實驗室，北京 102249；③海洋石油勘探國家工程實驗室，北京 100028； ④華北油田公司勘探開發研究院，河北任丘 062552)

0 引言

裂縫是影響油氣藏巖石物性參數的重要因素，精確預測裂縫對油氣勘探、開發具有重要意義[1-2]。不同尺度的裂縫對地下油氣藏的影響程度不同，基于疊后地震數據預測的大尺度裂縫(斷裂)通常改變油氣的儲存狀態[3-5]，因此精確預測大尺度裂縫是油氣勘探的重要組成部分[3]。

疊后地震數據與儲層地質信息具有相關性[6-8]，大尺度裂縫使疊后地震數據波形明顯突變或不連續[4]。提取有效的疊后地震屬性，可從幾何動力學角度預測儲層中的大尺度裂縫。常用的疊后地震屬性主要有相干體(描述波形相似性)[9-13]、曲率體(表征構造應力引起的地層彎曲程度)[14-16]、傾角體(刻畫地層構造變化特征)[17]等。然而，僅僅依靠單一屬性很難準確預測地下裂縫分布情況，因此屬性融合技術顯得極其重要。通過數學方法綜合考慮多種屬性特征，將它們組合為更全面、可靠的裂縫表征屬性，可以降低單一屬性預測的多解性[18-20]，提高裂縫預測精度。

目前，屬性融合方法較多，且應用較廣泛。在屬性色彩技術方面，Guo等[21]將屬性分量映射到色彩模型中，通過紅、綠、藍(Red-Green-Blue, RGB)和色調、亮度、色飽和度(Hue-Intensity-Saturation, HIS)模型進行屬性融合；為了準確確定融合屬性，丁峰等[22]結合主成分分析與紅、綠、藍、透明度(Red-Green-Blue-Alpha, RGBA)顏色融合方法分析屬性融合，很好地識別了斷裂區域。在神經網絡方面，徐麗萍[23]利用人工神經網絡方法進行非線性融合，以預測儲層的發育程度。曹琳昱等[24]將粒子群優化的BP神經網絡方法用于屬性融合，但需要優選屬性訓練網絡，且會陷入極小值。李全忠等[25]首次利用脈沖耦合神經網絡(Pulse Coupled Neural Networks, PCNN)進行地震屬性融合，以指示油氣發育情況，然而PCNN模型中的大量參數需要人為干預設置，導致融合結果不準確及不能準確突出單屬性的細節特征。因此，參數自適應PCNN(Parameter-Adaptive PCNN, PA-PCNN)模型[26]應運而生并用于圖像融合領域，很好地避免了人為設置參數帶來的誤差。此外，基于多尺度幾何分析的PCNN模型在圖像融合領域的應用效果很好，通過非下采樣小波變換[27]或非下采樣剪切波變換[28](Non-Subsampled Shearlet Transform,NSST)分割原圖像，可更好地提取細節信息進行融合?；贜SST-PCNN模型的多信息融合技術廣泛用于醫學[29-30]、遙感[31-32]等領域，且融合效果尤為突出。

本文在前人理論研究的基礎上，結合NSST和PA-PCNN的優點，建立了基于NSST-PAPCNN的屬性融合裂縫預測方法，以降低屬性多解性，消除原屬性中的部分冗余成分，可最大限度地保留有用信息，為地質解釋提供相對準確的裂縫預測數據。首先，通過NSST將多屬性分解為高、低頻子帶，其中高頻子帶包含更多的裂縫細節信息，低頻子帶可更好地刻畫裂縫輪廓且具有豐富的能量信息。其次，對高頻子帶運用PA-PCNN模型進行融合，無需人工設置參數，得到更全面的高頻數據；結合八鄰域的改進拉普拉斯算子加權和(Weighted Sum of Eight-neighbor-hood-based Modified Laplacian，WSEML)與局部能量加權(Weighted Local Energy，WLE)方法對低頻子帶進行融合，使低頻數據更好地保留細節及能量信息，以得到豐富的低頻數據。最后，通過逆NSST方法完成屬性融合裂縫預測。應用實例較好地證明了本文方法的有效性，通過對比不同方法的屬性融合裂縫預測效果，突出了所提方法的優勢。

1 理論方法

1.1 NSST

屬性融合過程中，為了獲得細節信息更豐富的結果，通過數學變換進行多尺度、多方向分解提取相同位置的不同屬性、不同空間細節信息進行融合。NSST具有位移不變性及方向靈敏性等特點[32]，計算相對簡單，能夠準確提取目標邊緣及空間信息，在醫學和圖像處理領域應用廣泛。因此，將其應用于裂縫單屬性分解，提取細節信息進行融合，可以更全面、準確地預測裂縫。

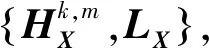
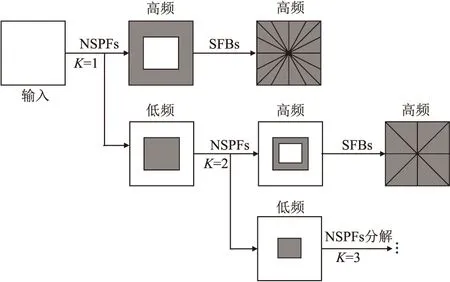
圖1 NSST分解框架

對高、低頻子帶分別融合后的數據運用逆NSST進行數據組合重構，主要分兩個步驟：首先，通過SFBs對各個方向分解的濾波結果進行累加，生成非下采樣金字塔；然后，使用重構濾波器對非下采樣金字塔由粗到細地進行數據組合重構，獲得融合后的數據結果。

1.2 PA-PCNN高頻子帶融合

PCNN是一種基于文獻[33]的皮質模型，是依據哺乳動物大腦皮層中同步脈沖發放的現象提出的，具有全局耦合和脈沖同步等特點，適用于數據融合領域。

PCNN模型是由若干神經元連接而成的單層反饋網絡[34]，輸入的單個屬性中數據的個數與神經元一一對應，每個神經元都受相鄰神經元影響，從而進行信息傳遞和耦合，且主要由接收、調制和脈沖發生三部分組成。在傳統的PCNN模型中，存在大量的自由參數設置且非線性較強，求解過程繁瑣、計算量大，因此簡化的PCNN模型[26]應運而生。

簡化的PCNN單個神經元工作流程(圖2)可描述為

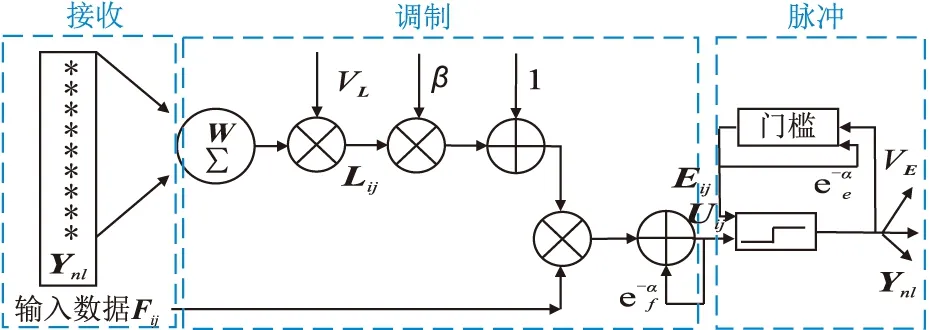
圖2 簡化的PCNN工作流程

Fij(η)=Sij

(1)

(2)

Uij(η)=e-αfUij(η-1)+Fij(η)[1+βLij(η)]

(3)

(4)

Eij(η)=e-αeEij(η-1)+VEYij(η)

(5)

式中：Fij(η)為第η次迭代后(i,j)位置的反饋輸入項；Sij為(i,j)位置輸入數據；Lij為連接項，將周圍神經元依據不同權重值相連；Ynl為周圍(n,l)位置神經元的輸出脈沖值；Wijnl為(i,j)位置輸入數據周圍(n,l)位置神經元的權重；Uij為內部活動項，e-αf×Uij(η-1)為上一次內部活動的衰減項，e-αf為Uij(η-1)的指數衰減系數；Fij(η)[1+βLij(η)]為反饋輸入和連接項的非線性調制，β為連接系數；e-αe為Eij(η-1)的指數衰減系數；Eij為動態閾值項；VL和VE分別為連接項和動態閾值項的幅值。

在式(1)～式(5)中，主要涉及五個自由參數(VL、αf、β、αe、VE)和一個權重矩陣(Wijnl)。在常規方法中，這些參數往往都由人為設定，會導致不準確的融合預測結果。因此本文運用PA-PCNN方法，無需人為設定，根據輸入數據自有特征自適應地求解參數進行融合處理。分析式(1)～式(5)可知，β和VL可以整體視為連接項的權值系數，因此定義κ=βVL為連接權重強度。此外，權重矩陣主要計算周圍神經元對目標神經元的影響作用，可通過距離定義權值。根據文獻[26]可知，所有自由參數都通過自適應計算獲得，即

(6)

(7)

(8)

VE=e-αf+1+6κ

(9)

(10)

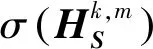
為了便于求解計算，需將權重矩陣近似為

由上述PA-PCNN過程得到每個屬性迭代后在所有神經元處產生的脈沖點火次數，由此可以獲得各個神經元處的融合權重系數

(11)

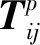
(12)

1.3 WSEML+WLE低頻子帶融合

經過NSST分解后的各屬性數據低頻子帶包含大量能量和細節信息，因此低頻段的融合策略對最終融合質量具有重要影響。傳統方法通常直接對低頻數據進行簡單加權平均融合，然而不同屬性在同一位置的能量不同，易造成低頻融合結果能量損失。為了在低頻融合數據中盡可能保留原數據能量和細節信息，引入WLE和WSEML算法融合低頻子帶數據[35-36]。

WLE算法根據區域內各數據之間的相關性，最大限度地保留原數據能量信息

LS(i+u,j+v)2

(13)

式中：W是大小為(2R+1)×(2R+1)、半徑為R的權重矩陣，矩陣中每個元素值設為22R-r，其中r是(i,j) 位置到矩陣中心四鄰域的距離；LS為NSST分解后各屬性的低頻子帶。以一個3×3階矩陣為例，設R=1，r=0,1,2，則

由于計算效率問題，對NSST分解層數進行一定限制，因此低頻子帶中仍然包含一定細節信息。為了盡可能地保存原數據中的細節信息，引入WSEML算法

R+1)×EMLS(i+u,j+v)

(14)

其中

EMLS(i,j)=|2LS(i,j)-LS(i-1,j)-LS(i+

1,j)|+|2LS(i,j)-LS(i,j-1)-LS(i,j+1)|+

(15)

結合WLE和WSEML算法，充分提取了原屬性數據中的能量和細節信息，可求取低頻子帶融合權重，最終獲得低頻子帶數據

(16)

(17)

1.4 算法實現流程

根據上述理論算法，總結了NSST—PAPCNN屬性融合裂縫預測結構框架的具體流程(圖3)。

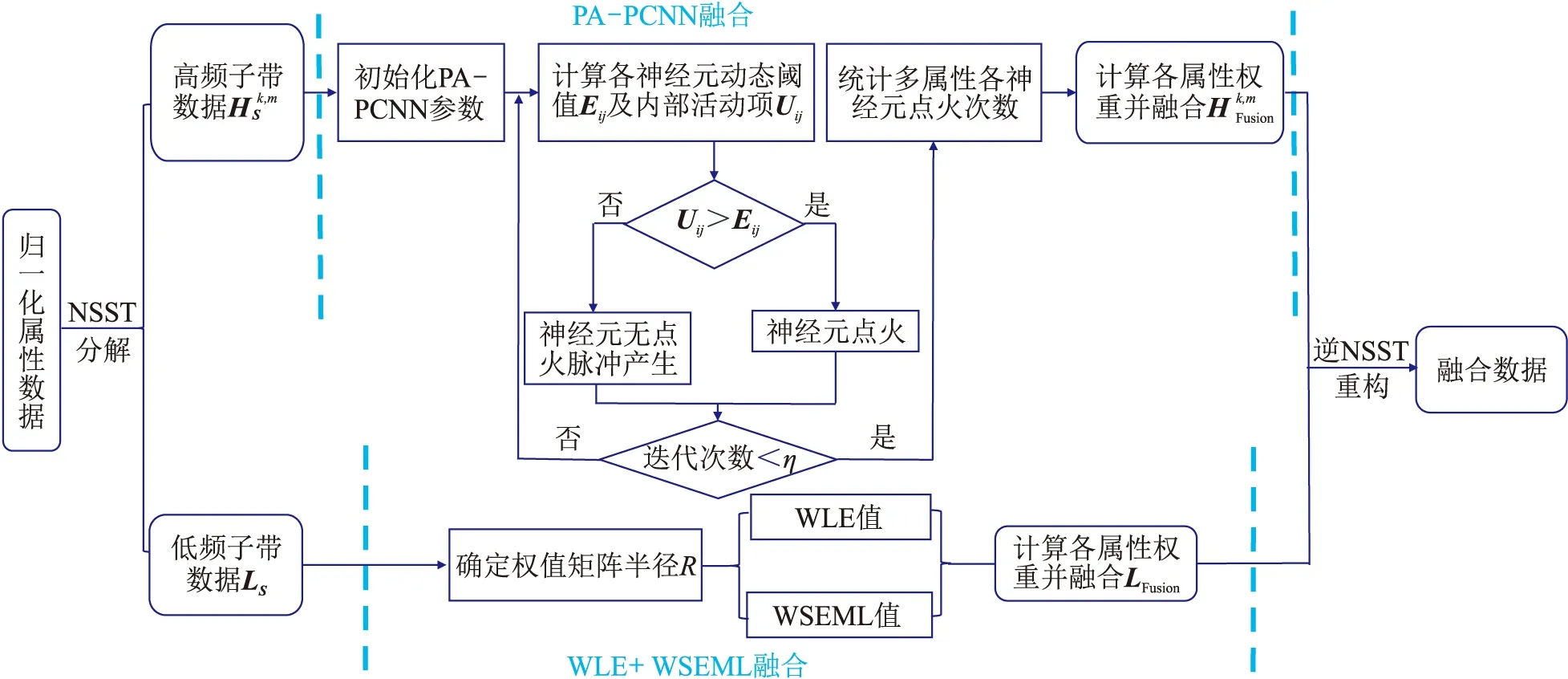
圖3 NSST-PAPCNN屬性融合裂縫預測結構框架

(1)從疊后地震數據中提取表征大尺度裂縫的屬性(包括相干A、最大曲率B和傾角C)，并對各屬性數據進行歸一化處理。由于不同的屬性其量綱及數量級不同，不能直接融合，需要將多屬性數據歸一化到[0，1]。

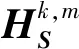
m∈[1,M(k)]

數據分解過程中需要確定分解的層數K及每層方向數M(k)。

(4)對各屬性低頻子帶進行WLE+WSEML融合，最大限度地保留能量和細節信息。融合前，需確定式(13)中的權重矩陣半徑R，最終得到融合的低頻子帶LFusion。

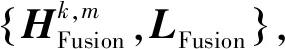
2 應用實例

為了驗證NSST-PAPCNN多屬性融合裂縫預測方法的可行性和有效性，對M區地震數據進行測試，數據范圍為Crossline1～Crossline751、Inline1～Inline751。該區裂縫較發育，大尺度裂縫(小斷裂)分布廣泛。為了有效預測大尺度裂縫，從疊后地震數據中準確提取了目的層段的相干、最大曲率和傾角等三種屬性，并分別做歸一化處理，然后進行屬性融合處理，具體過程(圖4)如下。

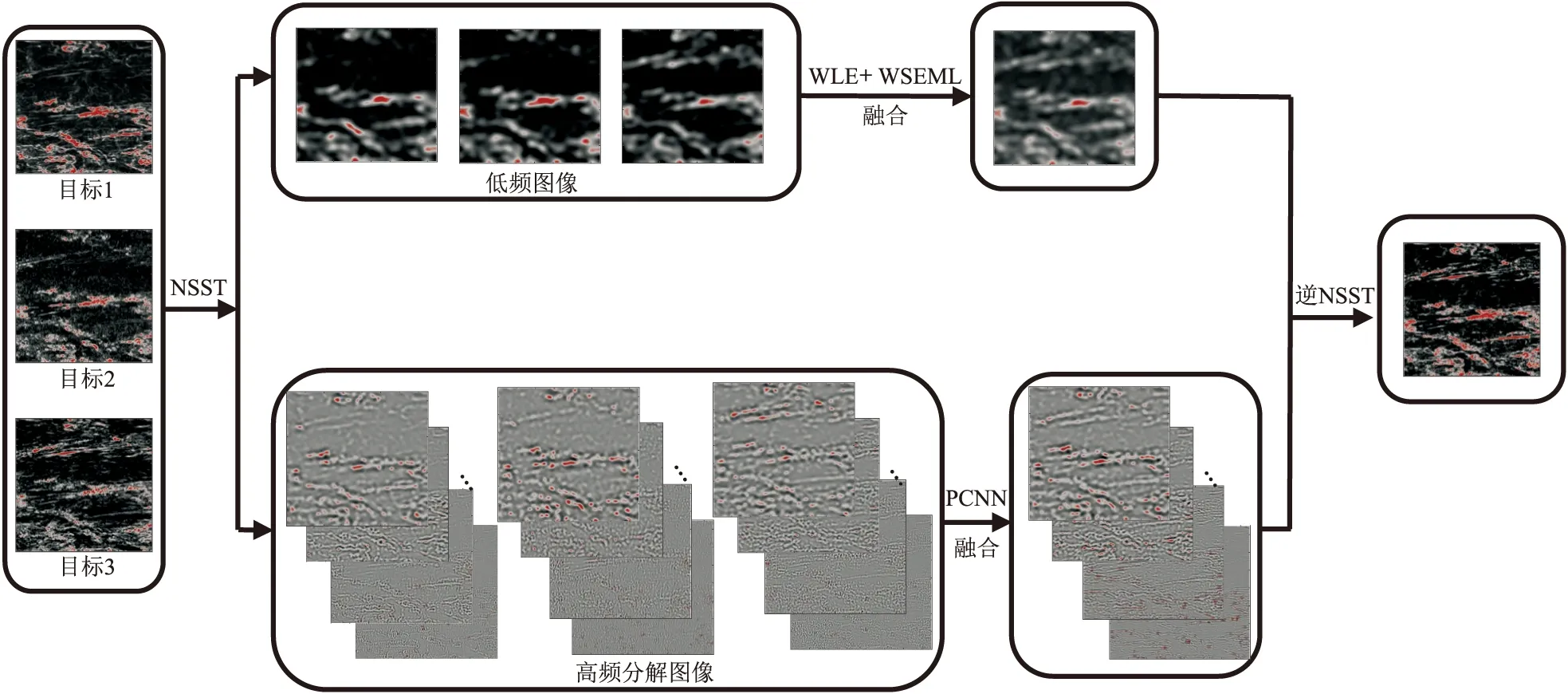
圖4 M區多屬性融合步驟

(1)將三種屬性分別進行NSST多尺度、多方向分解處理。測試并分析該區的數據特征可知，分解的層數超過4時，計算較穩定，但是層數過多會導致計算耗時較長。經權衡計算效果及效率，設定分解層數為5，每層的分解方向由細到粗為{16,16,8,8,4}。

(2)對分解后的高頻子帶數據進行PA-PCNN融合。測試結果表明，迭代次數過多，融合結果差異不明顯。因此通過試驗，選取迭代次數為110。融合前，需要將PCNN模型中的各項參數初始化為0，并根據實際數據特征自適應地計算各融合參數。通過點火次數確定各屬性高頻子帶數據權重系數，融合得到最終高頻子帶。

(3)對分解后的低頻子帶數據進行WLE+WSEML融合。綜合考慮計算效率及對結果的影響程度，設定式(13)中權重矩陣半徑R為1，計算相應的WLE及WSEML值，并確定各屬性低頻子帶數據權重系數，融合得到最終低頻子帶。

(4)對分別融合后的高、低頻子帶數據進行逆NSST重構，獲得最終的屬性融合結果。

由M區歸一化疊后均方根振幅屬性切片(圖5)可以大致看出裂縫的發育特征，以此驗證融合結果。為了更全面、準確地預測裂縫，需要最大限度保留三種屬性的輪廓、能量及細節特征。圖6為M區目的層段歸一化屬性切片，圖7為相干、最大曲率和傾角多尺度、多方向分解的部分切片。由圖可見，本文的NSST-PAPCNN方法能夠對三種屬性進行多尺度、多方向分解，充分提取了裂縫細節及能量信息，分別獲得了低頻(圖7a)、淺層分解(粗化分解，圖7b)、中層分解(逐漸細化，圖7c)及深層分解(細化分解，圖7d)等信息，從而得到了全面表征裂縫信息的融合結果。

圖5 M區歸一化疊后均方根振幅屬性切片

圖6 M區目的層段歸一化屬性切片(a)相干；(b)最大曲率；(c)傾角屬性數值越大，則裂縫越發育，紅框區域展示了三種屬性的明顯差異

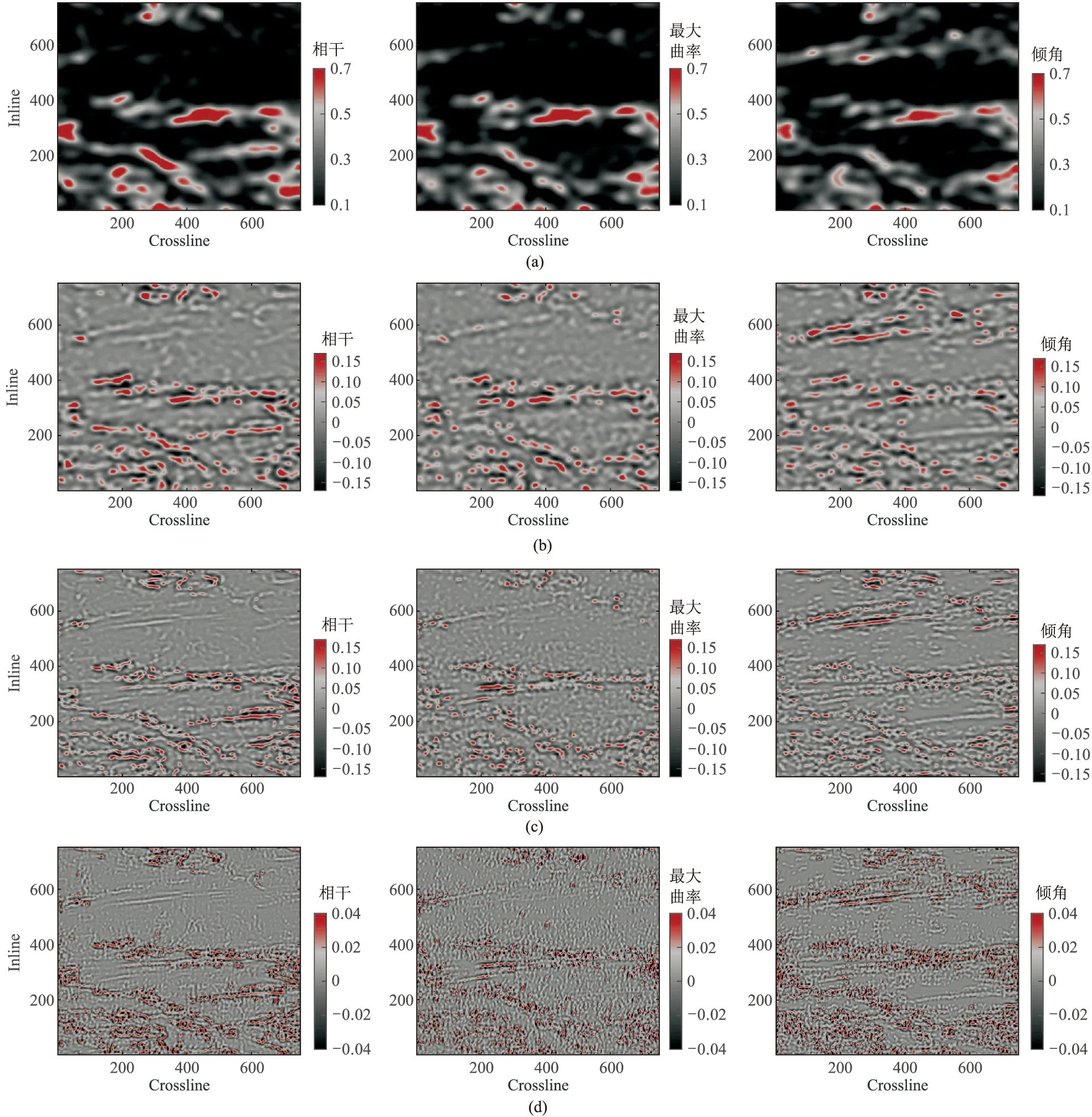
圖7 相干(左)、最大曲率(中)和傾角(右)多尺度、多方向分解的部分切片(a)低頻分量；(b)淺層分解；(c)中層分解；(d)深層分解

為了驗證NSST—PAPCNN方法的屬性融合裂縫預測效果，對比了不同方法的屬性融合裂縫預測結果(圖8)。對比圖8與圖5可見， NSST-PAPC-NN方法具有明顯的優勢，消除了部分冗余成分(圖8a紅框區域)，很好地保留了原屬性的能量、輪廓及細節信息(圖5)，全面刻畫了大尺度裂縫的發育情況，為地質解釋人員提供了較精確的裂縫預測數據。實際數據測試結果表明，本文提出的基于NSST-PAPCNN的屬性融合裂縫預測方法能夠更有效地預測裂縫。

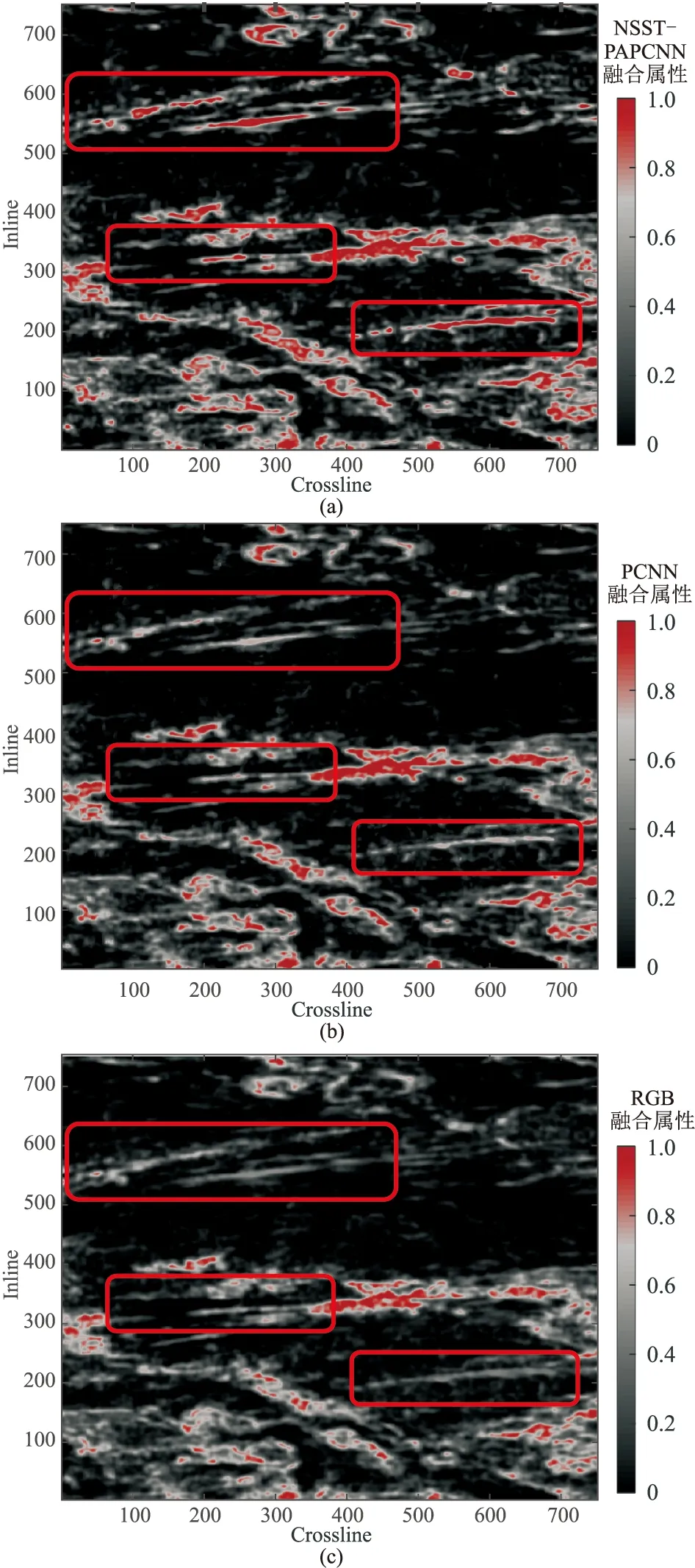
圖8 不同方法的屬性融合裂縫預測結果(a)NSST-PAPCNN；(b)PCNN；(c)RGB紅框區域展示了三種結果的明顯差異

3 結論與建議

本文基于NSST及PA-PCNN方法提出了一種屬性融合方法用于裂縫預測。該方法基于NSST分解算法，將多種屬性數據分解為高、低頻子帶，對融合后的多尺度、多方向高、低頻子帶進行數據重構，得到最終的多屬性融合結果，可進一步提取裂縫的輪廓及細節信息。

針對包含豐富細節信息的高頻子帶數據，采用PA-PCNN算法自適應調節自由參數，降低人為設置帶來的誤差。根據各子帶數據各元素的點火脈沖產生次數，確定融合系數進行高頻子帶融合。針對包含能量、輪廓及殘存細節信息的低頻子帶，結合WLE和WSEML算法，最大限度保留低頻子帶的能量和細節信息，確定融合系數進行低頻子帶融合。

將融合后的高、低頻子帶數據進行逆NSST重構，獲得最終的融合結果，降低了原屬性的多解性，消除了部分冗余成分，很好地保留了原屬性的細節和能量信息，能夠綜合多屬性特征，全面、準確地預測裂縫，從而為地質解釋人員提供較為精確的裂縫預測數據。運用本文方法對M區屬性數據進行測試，并對比了不同方法的屬性融合裂縫預測結果，證明基于NSST-PAPCNN的屬性融合裂縫預測方法能夠更有效地預測裂縫。

尚需指出，所提方法由于需要經過NSST多尺度、多方向分解，并對各尺度、各方向數據分別進行屬性融合，導致計算量較大，耗時較長。因此，經權衡計算效率和融合效果，認為NSST分解的層數不能過多。此外，在盡量保留原屬性中的有用細節成分時，往往無法保證融合后的所有細節信息都可靠，因此還需要依靠地質解釋人員的專業經驗及實際工區的數據特征準確預測裂縫，以進一步降低細節信息的多解性。