基于改進式k-prototypes聚類的壞數據辨識與修正

王孝慈，董樹鋒，劉育權，王莉，李俊格

(1. 浙江大學 電氣工程學院，杭州 310027； 2. 廣州供電局有限公司，廣州 510620)

0 引 言

隨著數據挖掘技術在工業用電領域的逐漸應用，準確的負荷數據變得至關重要。對于工廠來說，準確的負荷數據可以支持其負荷預測、需求響應等多種高級應用，從而提升用能的經濟性。另一方面，對于電力企業，準確的用戶用電數據可以降低其參與售電市場的風險，并避免用戶竊電帶來的經濟損失[1-2]。然而，由于設備停運、儀表故障、通信線路異常等原因，導致工廠負荷數據中存在大量壞數據，影響工廠和電力企業的正確決策[3]。因此，在對負荷數據挖掘之前，進行壞數據的辨識與修正非常重要。

目前，壞數據辨識與修正方法的研究主要針對系統負荷或母線負荷，主要方法有狀態估計法、橫向縱向比較法、聚類法。傳統的基于加權殘差或標準殘差的狀態估計法，容易出現殘差污染和殘差淹沒現象，造成壞數據的漏檢和誤檢[4-5]。橫向縱向對比法根據歷史負荷數據值確定正常數據范圍，對相鄰時刻的負荷數據值非常依賴，因此在一定程度上無法處理連續丟失或突變的壞數據[6-7]。聚類法通過提取用戶典型用電模式，確定每種用電模式下負荷數據的合理范圍完成負荷辨識，取得了不錯的效果[8-10]。文獻[8]利用快速爬山法改善模糊C均值(fuzzy C-means, FCM)聚類算法，改善了聚類數難以選擇，初始聚類中心隨機選擇等缺點，并根據每個用電模式中歷史負荷的最大最小值確定正常數據可行域完成壞數據辨識。文獻[9]利用極限學習機提取數據特征，并利用空間核密度聚類分析特征識別不良數據。但是，上述聚類的特征向量全部為負荷用電數據，在聚類向量中本身包含壞數據的情況下，聚類結果無法準確反映待測日的用電模式特征，會對數據辨識與修正造成影響。文獻[10]為了解決上述問題，提出了一種利用灰色關聯分析引入非負荷數據信息，改善FCM聚類的壞數據辨識與修正模型，實驗結果表明在聚類中引入非負荷數據特征值，可以提高模型的準確性和實用性。

文獻[11]指出在進行負荷模式提取時，不存在一種聚類方法普遍優于其他聚類方法。并且對于工業負荷模式提取，直接移植現有的聚類方法效果不佳，需要更有針對性的研究。文獻[12]采用統計模糊矩陣分類法對工業負荷進行分類，并通過非參數回歸分析方法提取中心負荷向量，進而構造異常數據域，完成負荷辨識。但該方法在落地時，需要海量數據，現有大部分工廠無法滿足其對數據存儲的要求。

針對上述不足，提出了一種基于改進式k-prototypes聚類的壞數據辨識與修正方法。主要貢獻在于：

(1)構建聚類特征向量時，考慮工廠用電特點，引入非負荷數據，削弱負荷數據中壞數據對聚類結果的影響；

(2)對標準k-prototypes算法進行改進，增加了多組初值并行擇優，改善了其容易陷入局部最優的缺點，并對聚類數進行自適應處理，解決了主觀選擇聚類數量的問題；

(3)結合聚類結果，提出了負荷可行域的計算方法，并基于質心曲線置換對壞數據進行修正。

算例分析表明，所提改進式k-prototypes聚類算法較FCM聚類算法在工廠用電模式提取的效果更好，應用到壞數據辨識與修復中，識別的召回率和修復的準確率都有所提高；較簡單置信區間壞數據識別、線性插值壞數據修復，效果提升顯著。

1 混合特征聚類

1.1 混合聚類特征選擇

利用負荷聚類算法進行壞數據辨識與修正的本質是提取用戶用電的行為模式，將不符合其行為模式的數據找到，并進行修正。然而用于聚類的工廠負荷曲線本身就包含壞數據，如果在聚類時，僅考慮負荷數據，會帶來兩個問題：

(1)聚類時，結果受負荷壞數據的影響大，無法對用戶用電的行為模式進行精確提取，從而影響負荷辨識與修正結果；

(2)修正時，對于某些用電數據嚴重缺失的時段，無法通過其他信息輔助對其進行填補。

基于上述原因，需要在特征向量中引入工廠的其他用電特征，修正工廠負荷時序值的聚類結果。工廠用電與其生產計劃、生產模式強相關。對于有規律性生產模式的大多數工廠，其生產活動一般按周開展，并受節假日影響。因此，需在特征向量中引入“工作日屬性”與“節假日屬性”。另外，部分工廠除生產用電外，空調用電占比最大，如輪胎工廠的空調用電可達其總用電量的20%～30%，空調用電量與氣溫強相。故在考慮溫度敏感度大的季度、空調負荷占比高的工廠時，需要增加“氣溫”特征維度。聚類特征選取結果如表1所示。

表1 聚類特征選取Tab.1 Clustering feature selection

1.2 k-prototypes算法

對于混合類型數據向量，同時包括數值型與非數值型數據。傳統的聚類算法會將非數值型數據數值化，在計算聚類損失函數時仍然使用歐式距離。這樣不但使非數值型數據脫離了本身的物理含義，還在聚類中引入了干擾因素。針對上述情況，選擇k-prototypes算法，在計算聚類損失函數時對數值型、非數值型數據分別進行考慮。

對含有n個向量的集合X={x1,x2,…,xn}，其第j個向量由一組特征值組成，可表示為：

(1)

式中xj,m為xj的第m個特征值;上標r表示數值型特征;上標c表示非數值型特征;mr為數值型特征的總數;mc為非數值型特征的總數。

通過k-prototypes算法將所有向量分為k類，則向量集合X可表示為：

(2)

式中Xi(i= 1, 2, …,k)為向量聚類后的第i類向量的集合。

向量聚類中，數值屬性的相似距離為歐式距離，非數值型屬性的相似距離為分類屬性距離[13]，則xj到其類心的距離可表示為：

(3)

式中xj所屬類Xi的中心向量為：

(4)

式中γ為非數值型變量的權重，可在數值數據分布距離標準差的1/3～2/3之間進行選擇[14]。

在聚類過程中，定義各個向量到所屬類中心的總距離為聚類損失函數，聚類的目標為使聚類損失函數最小，可表示為：

(5)

式中ni集合Xi中向量的數量。

1.3 改進式k-prototypes聚類過程

為了克服標準k-prototypes容易陷入局部最優，聚類數量難以選擇等缺點，對k-prototypes算法進行了如下改進：

(1)聚類過程中，隨機選取多組聚類中心初值，并行計算，選取代價函數值最小的作為聚類結果，解決陷入局部最優的問題；

(2)提取聚類效果關鍵指標，設定閾值，對聚類數量進行自適應處理，克服類別數選擇的主觀性;

(3)將向量數量較少的類拆散，向量合并到距離最小的其他類，避免算法將壞數據單獨分類，無法進行識別。

改進后的k-prototypes聚類主要過程如圖1所示。

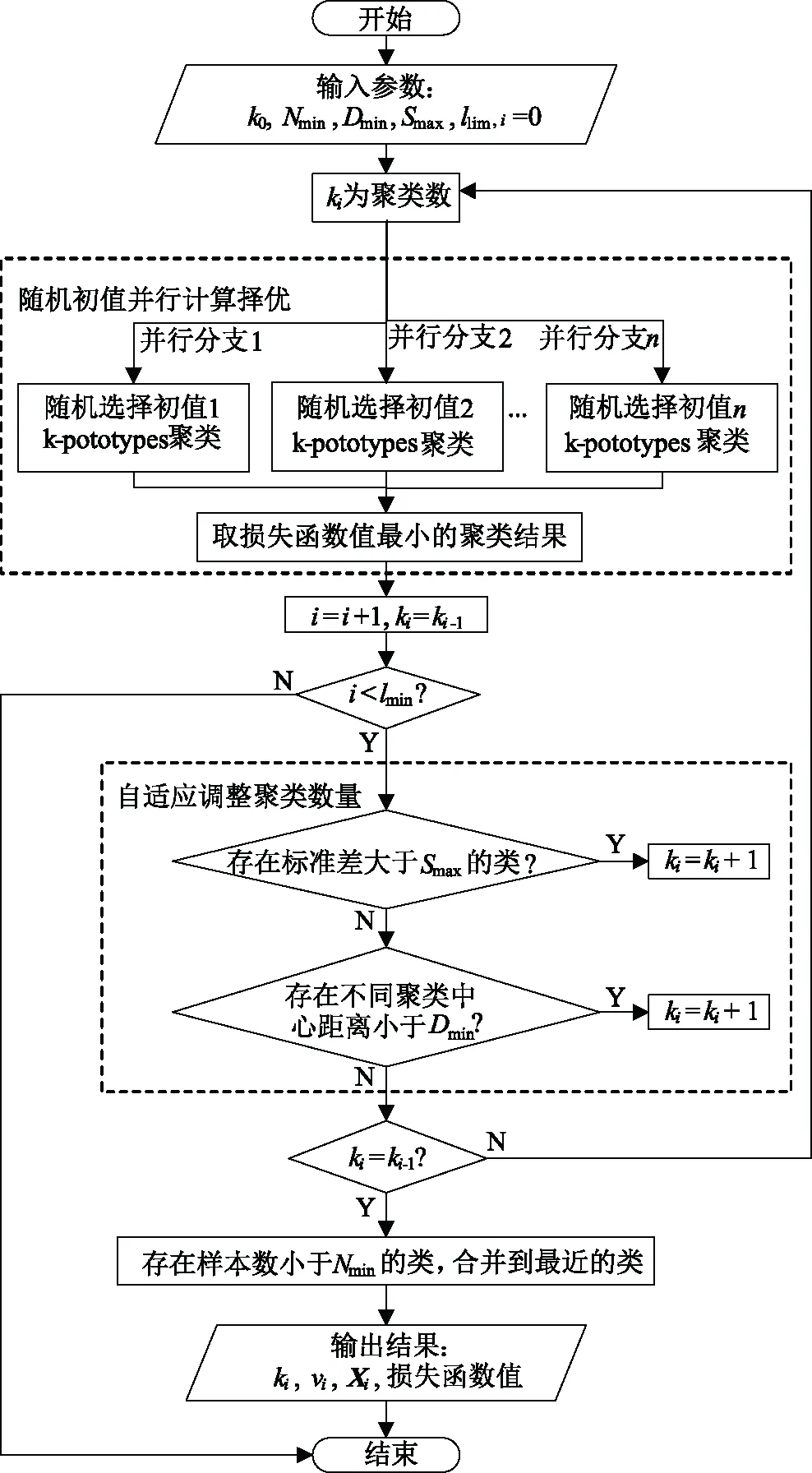
圖1 改進式k-prototypes聚類流程圖Fig.1 Flow chart of improved k-prototypes clustering algorithm

對于其輸入參數進行如下說明：

k0為類數的初始值，由于算法對類數有自適應調整的過程，所以k0的選擇不會影響聚類的最終結果。但k0越靠近最終的聚類類數，算法的迭代步驟越少，運算速度越快；

Smax為每一類向量距離分布的最大標準差，若某類的距離分布標準差超過Smax，說明該類內部相似度較低，應進行拆分。Smax的選取可以根據聚類數據的標準差選取其5%～20%，其選值越小，類內越緊湊；

Dmin為不同聚類中心的最小距離，若兩類距離小于Dmin，則需進行合并。Dmin的選取可以根據聚類數據的平均距離選取其10%～20%，其選值越大，類間分隔越明顯；

Nmin為每一類最少的向量數目，若少于此數，則不能作為一個獨立的類。Nmin的選取可以根據聚類數據集的長度選擇其5% ～ 10%的數量，如果Nmin= 1則不對每類最少向量數目進行約束。Nmin的限制可以避免將包含大量壞數據的向量單獨分類，使其無法被辨識與修正；

llim為算法最大迭代次數。

2 壞數據辨識及修正

2.1 壞數據辨識過程

根據聚類結果，提取每類集合中每個向量的負荷數據。對于采樣點數量為s的負荷數據(若采樣間隔為15 min，則s=96)，向量xj的提取結果可表示為：

(6)

聚類中心向量vi的提取結果為：

(7)

數據提取后，對應分類關系不變，即若xj∈Xi，則pj∈Pi。

每類的負荷曲線具有相似性，即曲線形狀大致相似，且幾個峰谷時刻基本相同，可認為同一類型負荷曲線以vi*為中心成正態分布[15-16]。根據正態分布理論計算每類負荷功率的可行域，具體步驟如下：

步驟1：針對每一類負荷Pj，計算正態分布參數：

(8)

步驟2：利用步驟1獲得的參數，計算負荷曲線可行域的上下限：

(9)

步驟3：形成負荷分類的可行域矩陣，對于第i類負荷其可行域矩陣為：

(10)

2.2 壞數據修正

基于負荷曲線相似的性質，提出一種基于類心曲線置換的壞數據修正方法，其原理為用待修正數據曲線所屬的聚類中心負荷曲線的相應部分，根據待修正數據部分首尾差值等比伸縮，置換待修正的數據。如圖2所示。

圖2 數據修正示意圖Fig.2 Schematic diagram of bad data correction

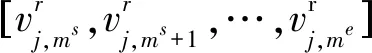
(11)

那么，修復后的數據可表示為：

(12)

2.3 方法應用流程

基于改進式k-prototypes聚類的壞數據辨識與修正方法如圖3所示。在進行壞數據的辨識與修復時，含有缺失數據的向量直接標記為待修復數據，不參與聚類，減小壞數據對聚類結果的影響。

圖3 方法應用流程圖Fig.3 Flow chart of method application

3 算例分析

算例數據集包括負荷用電數據、天氣數據、節假日數據。用電數據為廣州某工業園現場采集的3個工廠從2018年7月1日～2018年10月24日的負荷96點功率數據(去除光伏)。3個工廠在數據采集期間，以周為單位從事規律性的生產活動，并根據國家法定節假日調整生產模式。天氣數據為廣州市同期的平均氣溫，節假日數據來源于國家法定節假日。對負荷數據進行處理：

(1)制造空白數據：每個工廠隨機選擇10條日負荷曲線，將每條曲線的部分數據刪除，刪除數據部分連續，長度隨機且不超過整條曲線的40%；

(2)制造壞數據：每個工廠隨機選擇10條日負荷曲線，每條曲線隨機選擇3～20個點，升高或降低60%～70%。

根據1.3章節所述，選取改進式k-prototypes的算法參數，并結合具體工廠數據微調，如表2所示。

表2 改進式k-prototypes算例參數Tab.2 Example parameters of improved k-prototypes

3.1 改進式k-prototypes聚類效果

為測試隨機初值，并行擇優對k-prototypes算法陷入局部最優值的改善效果，對3個工廠進行仿真：選取不同的聚類數，從1逐漸增加并行分支數，記錄代價函數值的變化，并重復多次。

圖4為對空調廠聚類(k=5)，并行分支數從0增至50，重復實驗50次的效果圖。圖中每條曲線為一次實驗結果，較粗的曲線為多次實驗的平均值，數據點在底部形成的平行線為全局最優解。可見，隨著并行分支數量的增加，平均代價函數值逐漸趨于全局最優解；并且對于單次運行結果，隨著并行分支數量的增加，其代價函數值圍繞全局最優解的波動幅度越來越小。

圖4 優化后對陷入局部最優的改善Fig.4 Improvement of trapped local optima

利用改進式k-prototypes對工廠數據進行聚類，并選擇FCM聚類算法進行對比。FCM聚類算法在壞數據辨識與修正的研究中應用廣泛，較傳統硬聚類算法效果更好。空調廠的聚類結果如圖5所示，每條曲線為一條日負荷向量，較粗的曲線為聚類中心向量。由圖5可見，當聚類數相同時，此聚類算法由于引入非負荷數據削弱壞數據的影響，聚類效果更好：

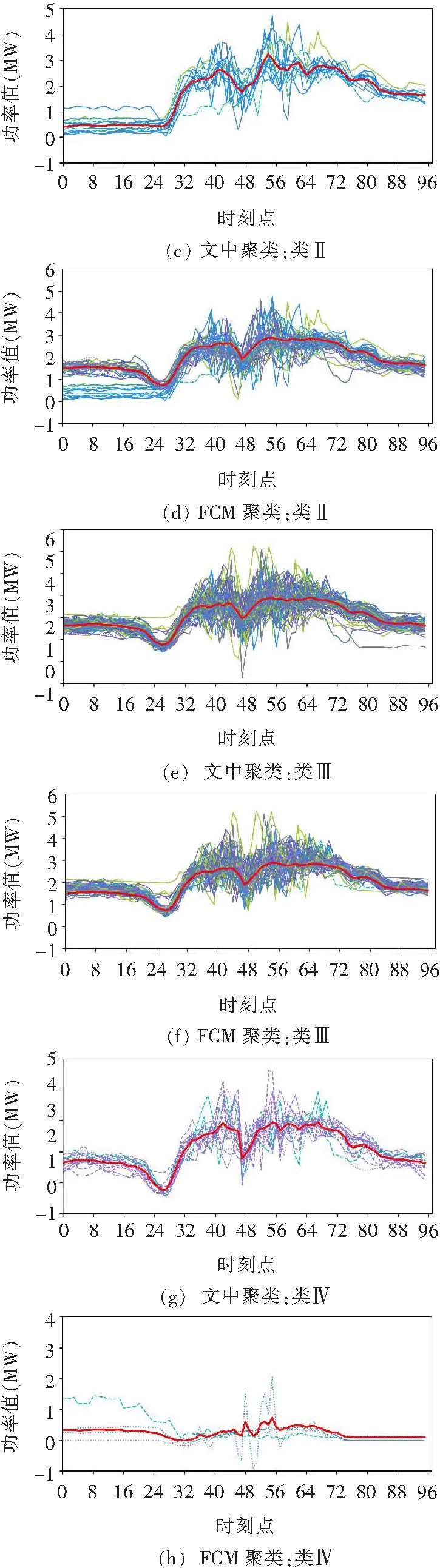
圖5 改進式k-prototypes與FCM聚類結果對比Fig.5 Comparison between the improved k-prototypes and the FCM clustering result

(1)每類向量數量更均勻，類內更緊致，不受異常數據影響單獨分類；

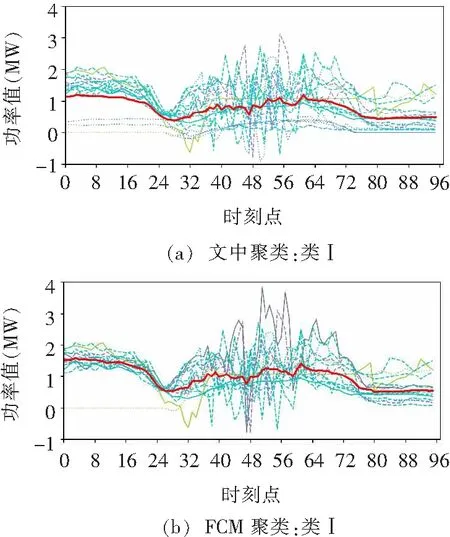
(2)不同類間分隔更明顯，聚類的類心向量有明顯區分，而FCM的類Ⅱ和類Ⅲ的中心向量比較相似。

3.2 壞數據辨識效果

不同的聚類結果會對壞數據的辨識效果產生影響[17]。圖6為空調廠某個壞數據的辨識結果，圖中虛線為計算的可行域。在文中算法中，壞數據所屬向量被分到類Ⅲ，由于其越出可行域，被成功識別出來；而在FCM聚類算法中，壞數據所屬向量被分到類Ⅰ，在該類可行域里，沒有被正確識別；如果不進行聚類，雖然壞數據可以識別出來，但是識別結果在置信區間邊緣，識別結果不穩定。

圖6 聚類結果對壞數據辨識的影響Fig.6 Influence of clustering results on bad data identification

對3個工廠的壞數據辨識結果進行統計，壞數據的召回率與辨識的準確率如表3所示。與FCM聚類算法相比，文中算法在準確率保持不變的情況下，能辨識出更多的壞數據，顯著提高了壞數據的召回率。相比于置信區間法，壞數據的召回率與準確率都有顯著提升。

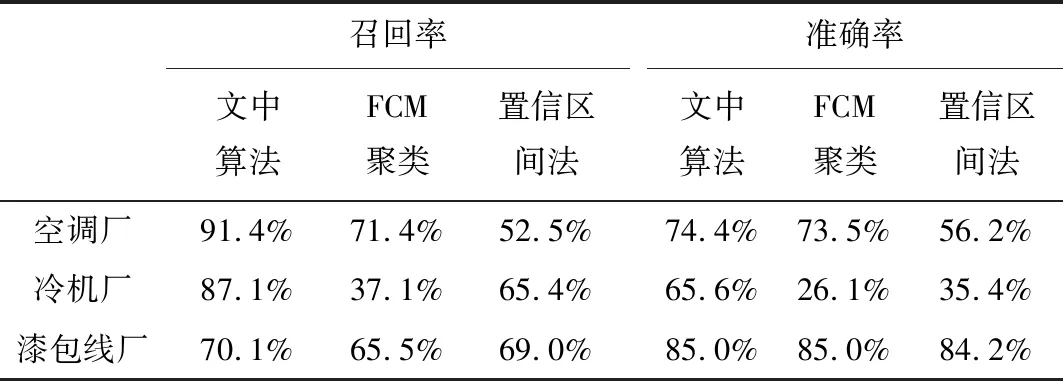
表3 壞數據辨識結果Tab.3 Bad data identification results

3.3 壞數據修正效果

利用所提的類心置換法對壞數據進行修正，通過與FCM+類心置換法比較，分析聚類對類心置換法修正準確率的影響；同時，對比線性插值法，分析所提基于聚類算法的類心置換法與直接插值法的修正準確率的區別。

如表4所示。對比基于FCM聚類的類心置換修正法，文中方法的修正準確率在空調廠、冷機場有少量的提高，在漆包線廠與其持平，可見聚類算法對修正準確率有一定影響。相比于線性插值法，所提類心置換法在修正數據時，由于考慮了數據變化趨勢，對壞數據修正的準確率有顯著提高。

表4 壞數據修正結果Tab.4 Bad data correction results

4 結束語

基于工業場景中混合數據集的聚類分析，提出了一種有效的壞數據辨識與修正方法。聚類過程中引入隨機選擇多組初值，并行聚類擇優，克服傳統k-prototypes算法容易陷入局部最優解的缺陷。并通過對聚類數的自適應處理，解決主觀選擇聚類數的問題。由于引入了非負荷數據，削弱了本身存在的壞數據對聚類結果的影響，使壞數據辨識的召回率和壞數據修正的準確率有所提高。

文中算法適用于大多數存在規律性生產模式的工廠，在實際生產過程中，一些小型工廠可能會根據需求缺口調整靈活的調整生產活動。后續的研究中，可進一步挖掘影響工廠生產活動的因素及其表征方法，應用到壞數據的辨識與修正的研究中。