“雙減”之下，“增效”至上
——初中數學作業設計點滴記錄

黃學娟

(合肥市第六十一中學 安徽合肥 230022)

華羅庚說：“學數學不做題目，等于入寶山而空返。”數學作業是課堂教學的延續和補充，是檢驗教學效果的重要手段。無效作業對學業的危害猶如垃圾食品對身體的傷害一樣。有效的作業設計應該具備合理化、個性化、多樣化、創新化等特征，使作業有“溫度”；尊重學生差異，使作業有“梯度”；注重貼近生活，使作業有“力度”；立足書本、拓展延伸，使作業有“尺度”。

一、分層作業

(一)難易分層

每位學生的情況各有不同。設計作業時要根據學生的差異因材施教，讓每位同學都能學有所獲、學有所成。適合的永遠是最好的，正如營養師檢查身體后會根據不同體質設計不同需求的飲食結構一樣，教師也需要根據學生的不同學習能力設計不同層次的作業。

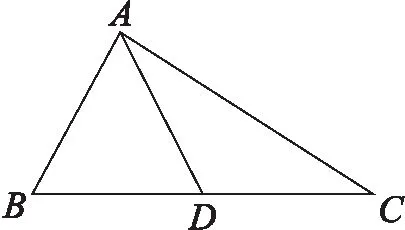
為此，每次的課堂練習筆者會按照A、B、C三個層次進行設計。對于A組同學，在學習“一次函數性質”時設計一次函數綜合應用方面的題目，在學習“角平分線”時設計如下題目：“已知：等邊三角形ABC.(1)P為△ABC內任一點，自點P向三邊所在直線作垂線PD，PE，PF，點D，E，F為垂足.求證：PD+PE+PF等于定值.(2)若點P在△ABC外時，情況如何？”這類題目有適當的拓展空間，也有一定的難度，有助于學有余力的同學思維能力的培養。對于B組同學，在學習“角平分線”一節知識后設計如下題目：“已知：如圖，D是△ABC的邊BC上的一點，且AB=BD=AD=DC。求∠B，∠C，∠BAC，∠DAC的度數。”此類題目主要考查學生對于數學概念的理解和應用，讓學生跳一跳能夠得著。對于C組基礎薄弱的同學，在學習“一次函數”章節時筆者設計了確定各種解析式里自變量的取值范圍的作業(有根號下含有自變量的，也有分母里含有自變量的，還有混合形式的解析式)。在“角平分線”一課設計的作業是：“如圖，已知BD平分∠ABC，AB=BC，點P在BD上，PM⊥AD，PN⊥CD，點M，N為垂足。求證：PM=PN。”這類題目是考試必考的，也是所有同學都容易掌握的。這些題目的練習有益于他們記憶新知，獲取快樂，增強自信。

(二)內容分層

作業根據內容的不同可以分為課前作業、課堂作業、課后作業三個類型。

課前幾分鐘首先溫故知新，然后預習展示，最后收集疑問。

課上在學生掌握基礎知識的前提下，對重點加以強化，對難點進行點撥，設計部分隨堂練習，由學生自主完成，利用課堂的有效時間檢驗每個層次同學對重要知識的掌握情況，對于易錯點或者難點，請A組的“小老師們”分別下位指導自己的小組成員。比如在“因式分解”這一課，在基礎的提公因式法、公式法學生都掌握的情況下，筆者設計了這樣兩道需要多次因式分解的題目：(1)ab2-ac2；(2)3ax2+24axy+48ay2。這兩題一般同學解答起來并不困難，但是部分基礎較差的學生一時半會很難解答。課堂上如果多次重復就會讓其他同學感覺枯燥，同時也會讓已經掌握的同學無所事事。于是筆者安排A組同學下位指導自己小組成員。這種同學之間的互助一來便于部分基礎較差的學生以放松的姿態迅速理解，二來可以以另一種無形的復習形式幫助優等生進一步鞏固課堂所學內容。這種小組互助的形式下，一部分優等生“先行一步”，再由他們帶動班級里其他同學一起前進，既高效又輕松。

課后作業的主要作用是鞏固課堂知識，提煉數學方法。每次課后作業應帶有一定的層次性，對于綜合性題目提出選做要求，主要提升學有余力的學生的數學學習興趣。比如在學完“因式分解”這一章節內容后，筆者在課后作業中設計了以下兩道題：

1.試說明(n+7)2-(n-5)2(n是正整數)能被24整除。

2.計算：

(1)(a-1)(a+1)=；

(a-1)(a2+a+1)=；

(a-1)(a3+a2+a+1)=；

(2)由此，猜想：(a-1)(a99+a98+a97+…+a2+a+1)=.

(3)請你利用上式的結論，求2199+2198+…+22+2+1的值。

這兩道題有一定的拓展性，特別是第2題，這種由特殊到一般的規律題是歷年來中考數學的熱點，有時也是一個難點。當然這類題目一般都是作為課外選做題，學生自愿選擇完成。

(三)題量分層

數學題目貴在精而不在多，在“雙減”每晚90分鐘的作業時間要求下，除了難度要控制外，數量也要重視。一般來說要給A組同學在適量的基礎鞏固題之外，額外增加一兩道拓展延伸題，題量不多，但是梯度有所體現。B組主要以鞏固和適當拔高為主，基礎題大概6題，鞏固拔高題大概2題。而C組則主要以書本的課后練習題為主，有時甚至是書本的例題，題量控制在10題以內。因為這組同學的能力不足，需要依靠一定數量的題目來強化對基礎知識的記憶。

二、個性化作業

馬斯洛認為“學生是獨立的個體”，同一班級的學生學習水平也參差不齊，教師應因材施教，從多個方面靈活設計個性化作業。個性化作業最大的優勢在于能夠調動學生完成作業的積極性，讓他們既能享受成功的喜悅，更能提高后續學習的信心，在自己的“最近發展區”獲得更大程度的提升。

(一)自選作業

教師根據知識難易設計不同層次作業，或者設計部分提高性作業，讓學生根據自身能力自由選做。比如在學完八年級上冊第13章第1節的內容后，筆者就在課后作業里設置了這樣兩道自選題。

1.已知：△ABC中，AB=5，BC=2a+1，AC=12，求a的范圍.

2.已知：圖(1)是五角星形，求∠A+∠B+∠C+∠D+∠E的度數；

圖(2)是七角星形，求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度數.

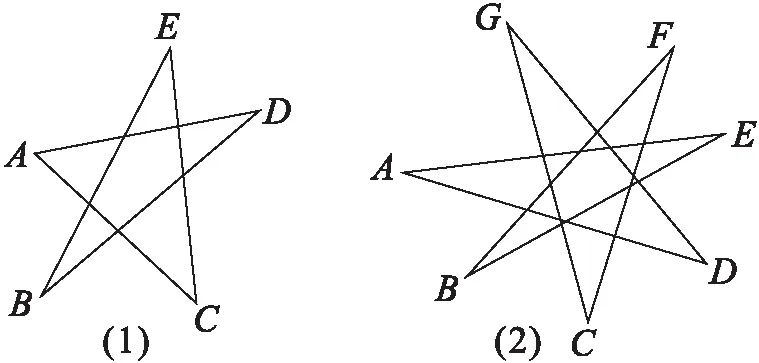
對于這兩道題目，筆者讓部分學有余力的同學挑戰一下自我，鼓勵其他同學完成，同時還設置了一定的挑戰基金，對那些勇于嘗試并積極思考的同學給予小小的獎勵。這類作業有利于幫助部分同學克服畏難情緒，尋找數學學習的樂趣。

(二)自制作業

除了常規作業，在一些節假日或寒暑假里，還可以讓學生嘗試自己設計作業。比如在國慶長假里讓班級A、B兩組的學生自制數學試卷，題目從平時用的《同步練習》或者書本課后習題中選擇。題型、題量、分值、難易程度提前告知。C層次的同學由于基礎較弱，可以根據書本知識點利用思維導圖形式進行整理，從而達到復習鞏固基礎知識的目的。返校后兩個班級進行評比頒獎，高質量試卷還將被老師“征用”，其他未征用的試卷可以作為能力相當的同學的交換作業。這樣A、B組同學既鞏固了自制試卷的知識，也了解了其他同學試卷的內容。而C組同學以另一種主動形式熟悉了書本知識，同時也提升了對數學學習的興趣。

(三)閱讀作業

鼓勵學生通過課外閱讀一些數學大家的故事，從中了解數學知識的誕生和探究過程。比如，在七年級時筆者推薦同學們閱讀《奇妙的數學王國》，八年級時推薦閱讀《數學讀本》等。同時教材中有關拓展內容，也可以讓一些“數學小達人”自主閱讀。比如滬科版數學八年級第57頁的“一次函數模型的應用”，對于學生進一步樹立函數的建模意識有很好的幫助作用。再如第147頁的“剪紙”內容，既是對軸對稱圖形的應用，也有利于對數學中的折疊問題以及動點問題的實踐感知。以上種種閱讀有利于提升學生們的自學能力，拓寬知識寬度和廣度。

(四)記憶作業

記憶作業包括一些數學定理、定義、公式和常見的無理數近似值。對于一些好題、難題的解題方法等，也要求學生記憶并會抽查一些同學復述。另外，對每次單元測驗里面的錯題，都會要求同學們進行書面訂正。然后教師檢查幾位小組長，小組長再檢查組員。

三、創新實踐作業

蘇霍姆林斯基認為，“所有智力方面的工作大都依賴于興趣”。在學習“軸對稱圖形”時筆者設計了作業“為自己的集錯本封面繪制一個具有軸對稱性質的圖案，同時為自己的設計寫一句有意義的話”。這種作業設計既體現了對集錯本的重視，又是對數學知識的創新應用，生動有趣，意義非凡。再如在學習“角平分線性質”和“線段中垂線性質”時，讓學生自己歸納添加輔助線的種類，對于一些學有余力的同學安排他們將自己的思考記錄下來，形成數學小論文。對于“不等式組解集的確定”和“特殊三角函數值”的記憶，讓學生們課下自己尋求記憶規律或者總結記憶口訣。同學們在創新作業的快樂完成中，逐漸養成善于觀察、思考、總結的好習慣。

數學來源于生活，應用于生活。在設計數學實踐作業時，應選擇切合學生實際生活的情境，加深他們對數學知識的體驗和感受。比如在每年寒假時可以設計用各種統計圖記錄家里年貨購置情況的作業。這樣既可以讓學生參與家庭生活事務，也可以通過數據了解一個家庭開支的主要方向。

四、彈性作業

彈性作業即靈活性作業，學生可以根據自我能力自由選做。比如每次在布置數學同步作業時，最后一兩道綜合性題目都是作為“選做題”要求，每一小節內容后的“拓展練習”也作一樣要求。對于那些主動積極完成的同學在第二天的課堂上點贊，肯定他們迎難而上的精神。在鼓勵積極探究同時也適當允許部分作業延后，實現彈性作業。

數學作業的設計需要拒絕機械、無效，鼓勵分層、個性、實踐、創新和彈性等。只有這樣才能有效落實“雙減”政策，實現“減負增效”目標，真正提升學生的綜合素養，讓學科教育重新回歸學校主陣地。