基于互補濾波的軌道不平順動態測量方法

陳仕明，魏世斌，李 穎，程朝陽，侯智雄，秦 哲，杜馨瑜

（1.中國鐵道科學研究院 研究生部，北京 100081；2.中國鐵道科學研究院集團有限公司 基礎設施檢測研究所，北京 100081）

軌道不平順是輪軌系統的激擾源，是引起機車車輛振動的主要原因，對行車的安全性、平穩性及舒適性等都有重要影響。軌道高低不平順會增加車體的垂向振動加速度和輪重減載率，軌向不平順會增加橫向振動加速度和脫軌系數［1］。因此，軌道狀態檢測對掌握軌道不平順特征分布、軌道養護維修策略及保障列車行駛安全具有重要意義［2］。

隨著列車速度提高，30～200 m 波長的軌道不平順逐漸開始影響列車運行安全。同時，對于大跨度橋梁與路基沉降的檢測需求也逐漸迫切［2］。軌道不平順檢測方式按照有無輪載作用，分為靜態檢測和動態檢測。靜態檢測結果是工務養護作業的依據，動態檢測結果是綜合反映軌道結構狀態的依據，例如線路中存在的道床暗坑和路基沉降等。按照測量原理，分為絕對測量和相對測量。絕對測量需依賴全站儀等精密測量儀器，以測量準確的高程信息，故檢測速度緩慢。相對測量主要分為弦測法和慣性基準法2 類，其中弦測法原理簡單，便于現場復核，缺點是測量波形在某些波段存在嚴重失真；慣性基準法是我國軌道檢查車在動態檢測中采用的主要方法［1］。傳統慣性基準法通過積分和高通濾波等算法處理加速度計和測距傳感器數據，實現對軌道不平順的測量。在測量長波不平順時，加速度計信噪比低，信號十分微弱，導致傳感器積分漂移誤差較大。因此，對長波不平順準確測量仍是亟待解決的問題。

我國對軌道長波不平順的測量主要采用德國的矢距差法。李陽騰龍等［3］在此基礎上提出了高密度四點偏差約束軌道高低模型。楊飛等［4］將矢距差法簡化為中點弦測法，提出用60 m 弦測量長波不平順。王源等［5］采用頻率抽樣逆濾波設計方法，對弦測測量的傳遞函數進行補償。此外，Tsubokawa等［6］為軌檢車設計“慣性中弦偏移”法，利用陀螺儀數據推導得到弦測值。另外，將組合導航的方法引入到軌道檢測中的研究方法越來越受到重視［7?9］。Chen 等［7］為相對測量軌檢小車集成衛星定位與慣性組合導航（GNSS/INS）技術，該方法脫離了全站儀等高精度設備，因此測量速度相對較快。Li等［8］在軌檢小車上配備激光輔助慣性導航系統，對鋼軌的三維曲線進行測量，但需要人為設置控制點。Jiang 等［9］克服了高精度控制點的要求，提出結合零速度更新技術的基于慣性導航的軌道不平順測量方法。這些方法通過引入其他傳感器作融合計算，可以測量得到軌道長波不平順。但往往系統復雜，要求檢測速度較低，且GNSS定位信號容易在過隧道時丟失，并不適用于高速列車的動態檢測。

利用車載傳感器進行高速動態檢測可有效提升檢測效率，是當前軌道檢查車上主要采取的方法。文獻［10?12］討論了采用安裝在構架上的陀螺儀測量不平順的方法，發現在低速條件下陀螺儀的測量結果更加準確。Westeon 等［11］指出該陀螺儀測量方法測量短波不平順時會產生衰減。熊麗娟等［13］分析了地球自轉對陀螺儀測量的影響。在此基礎上，Escalona 等［14］分析了采用加速度計和陀螺儀測量系統的傳遞函數，并引入組合測量方法，但采用的巴特沃斯濾波會帶來非線性相位變化。由于安裝條件限制，以上方法往往用車體或轉向架角度近似軌面角度變化，帶來的誤差降低了軌道長波不平順的測量精度。因此，Tsubokawa 等［6］在轉向架前后安裝測距傳感器以補償陀螺儀信號，并且為避免慣性傳感器積分漂移，提出用1 階差分描述軌道平順性變化。

本文提出一種應用于高速軌道檢查車平臺的軌道不平順動態測量方法。首先基于新型機械安裝結構，在軌面上構建“兩點弦”測量模型并推導出角速度測量算法；之后根據系統傳遞函數幅頻特性，設計互補濾波方法，以補償角速度測量法在短波不平順處的衰減；最后以檢測速度選定合適的測量算法。

1 傳統測量系統和方法

1.1 測量系統

軌道不平順測量系統主要由慣性測量單元（Inertial Measurement Unit，IMU）、激光器和CCD 相機集成的激光攝像組件及編碼器等傳感器組成［15］。當前廣泛應用的GJ-6 型軌道檢測系統將IMU 與激光攝像組件安裝在檢測梁上，根據編碼器脈沖信號對傳感器進行空間采樣，采樣周期為0.25 m［16］。其中激光攝像組件采用線結構光的三維視覺檢測模型，可解算出軌面特征點相對于相機的位移，分辨率高達0.1 mm。IMU 包含3 軸加速度計與陀螺儀，慣性傳感器由于受到積分漂移和列車振動的影響，測量誤差隨時間累積。

1.2 慣性基準法

動態測量基準坐標系以軌面中心點為坐標原點，x軸正向指向列車前進方向，y軸正向沿水平方向向左，z軸正向垂直于大地向下。

在實際工況條件下，由于轉向架與軸箱之間存在一系懸掛，檢測梁上的加速度計只能反映轉向架的位移變化。因此，利用激光攝像組件提供的測距信息測量軌面與轉向架之間的相對位移，并與加速度計信號結合，計算得到軌道不平順值。該算法表示為

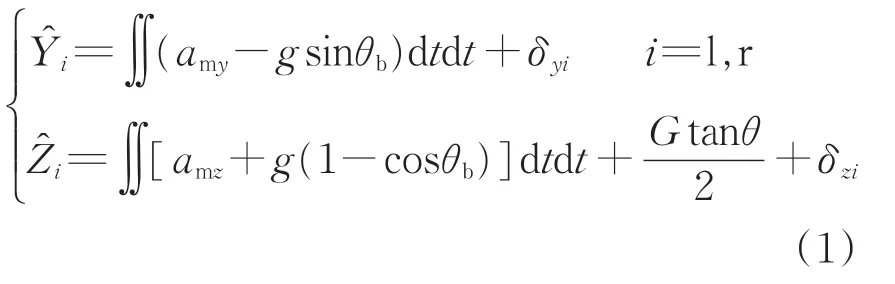
式中：和分別為軌向和高低不平順的測量值；am為加速度計測量值；g為重力加速度；θb為轉向架側滾角；t為時間；G為標準軌距值，即1 435 mm；δyi和δzi分別為測距傳感器輸出的橫向和垂向位移；l和r分別為左右2側。

式（1）給出的基于加速度信號和測距傳感器數據的高低和軌向不平順的慣性基準法常應用于傳統的軌道檢測系統，本文稱之為加速度測量法。在實際應用中，加速度計測量高低不平順時，理論上敏感軸需要始終與水平基準線相垂直，但轉向架運行過程中會產生6 個自由度的車體振動，加速度計敏感軸方向發生隨機變化。這種方法在測量短波軌道不平順時具有較高精度；在測量長波軌道不平順時，加速度計敏感值小、信噪比低，積分漂移誤差較大，測量精度有所下降；在低速檢測環境下，時間域采樣率降低，測量結果會迅速漂移。

2 測量系統和方法優化

2.1 系統優化

在GJ-6 型檢測系統的基礎上優化了機械安裝結構，如圖1所示。新系統統一設計了轉向架與檢測梁，并在轉向架前后的2 個端部安裝檢測梁，并在檢測梁中安裝激光攝像組件與IMU。理論上，該系統可以利用光纖陀螺儀具有的低漂移和高精度的特點，提升系統測量精度。

圖1 機械安裝結構

2.2 角速度測量法

基于改進的硬件結構，考慮光纖陀螺儀測量誤差項，推導角速度測量法。由于檢測梁與轉向架固定連接，因此對應的測量模型只考慮轉向架與軸箱之間的一系懸掛，測量模型如圖2所示。圖中：ψ為軌面切線俯仰角，即軌道的垂向切線與軌面縱向基準線x軸之間的夾角；?為軌面切線搖頭角，即軌道的水平切線與軌面縱向基準線x軸之間的夾角；ψb和?b分別為轉向架的俯仰角和搖頭角；x處的高低軌道不平順為Z（x），軌向不平順為Y（z）；x和x-L位置處軌頂點連線構成的“兩點弦”，在基準坐標系下的俯仰角記為ψ′，搖頭角記為?′；v為行車速度。

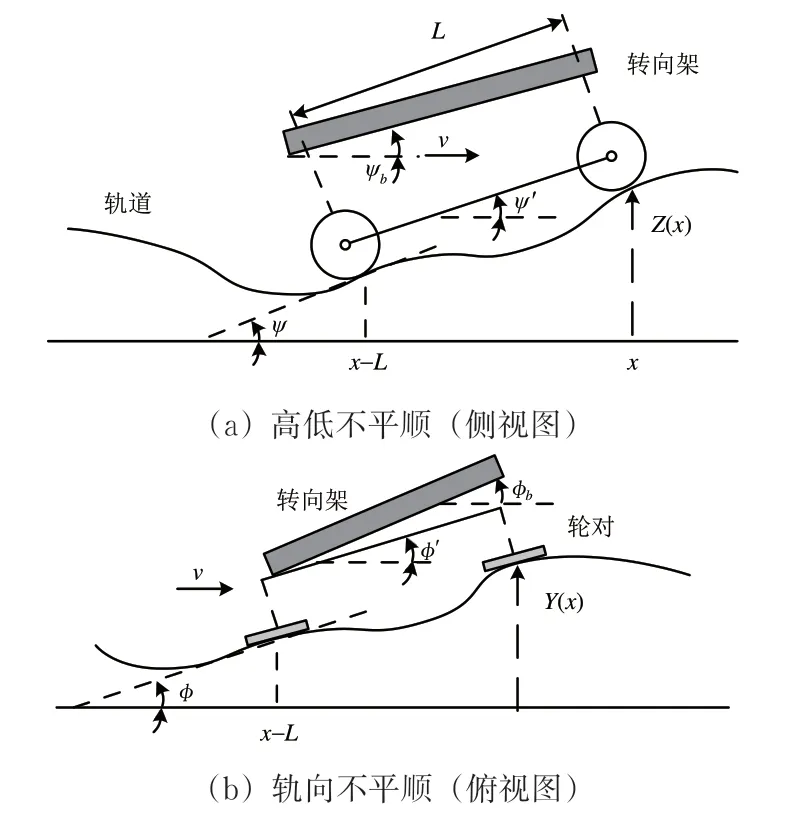
圖2 軌道不平順測量模型

根據文獻［11］可知，基于角速度測量軌道不平順（包括高低和軌向不平順）的簡化表達式為

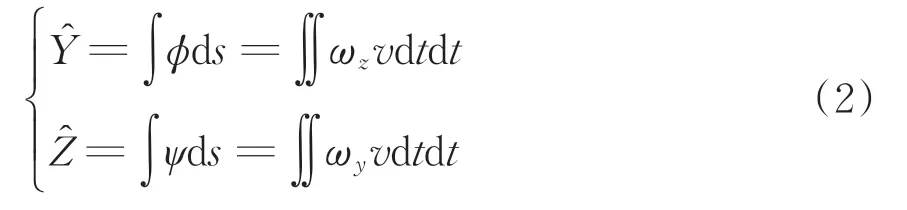
式中：ds為空間域微分算子；ωy為ψ的1 階微分；ωz為?的1階微分。

由式（2）可知：對于高低不平順的測量，可以通過對角度ψ的空間域積分得到；對于軌向不平順的測量，可以通過對角度?的空間域積分得到。

以高低不平順測量為例，由于轉向架與車輪之間存在一系懸掛，軌面切線俯仰角ψ難以通過安裝在檢測梁上的傳感器直接測量獲得，一般采用轉向架姿態角ψb對ψ進行近似［11?12］。測量30 m 以內的短波不平順時，近似引起的誤差較小；測量中長波不平順時，陀螺儀理論信號微弱，近似誤差導致信噪比較低，尤其是當列車與軌道之間存在共振時。

在測量高低不平順時，用ψ′代替ψ代入到式（2）進行測量計算；同理，測量軌向不平順時，用?′代替?，代入到式（2）。由圖2可知，角度ψ′和?′可使用當前安裝的傳感器進行觀測。設定ψ′和?′的1 階微分表示為ω′y和ω′z，設定γz=ψb?ψ′，γy=?b??′，2 者的1 階微分分別表示為和。因此，角速度測量算法可以表示為

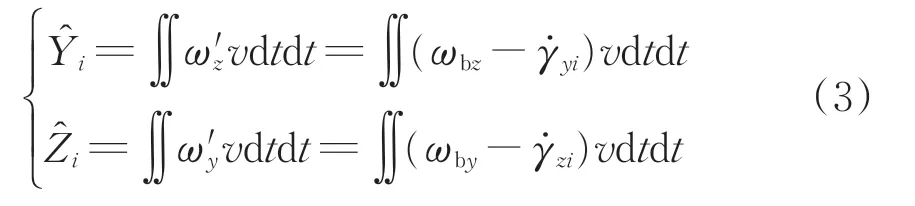
式中：ωb為轉向架三軸角速度。

激光攝像組件測量轉向架與軌道之間的相對位移測量模型如圖3所示。圖中：L為前后檢測梁的縱向距離；δB，y，r為后右側相機相對于軌面的橫向位移，δF，z，l為前左側相機相對于軌面的垂向位移，其余變量類似。由圖2和圖3可知，變量和可以表示為

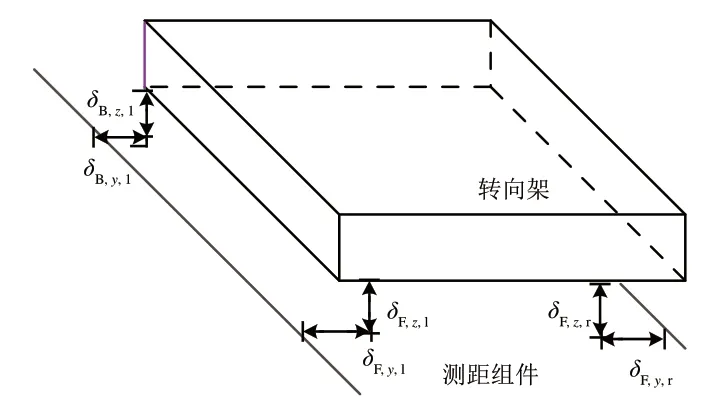
圖3 測距組件測量模型示意圖

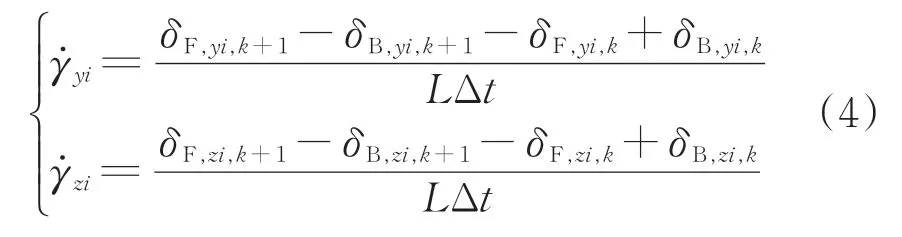
式中：Δt為2次空間采樣時間間隔；k為離散時間。

軌道檢測中一般采用歐拉角描述轉向架姿態，三軸分別表示為θb，ψb和?b。轉向架3 軸角速度ωb與陀螺儀測量角速度ωm的等式關系參考文獻［17］，考慮到列車行駛過程中轉向架姿態變化規律，忽略掉式中的2 階項，并將余弦項近似為1，可以簡化為

另外，考慮到地球自轉對光纖陀螺儀測量的影響，對誤差項進行補償。陀螺儀測量角速度在載體坐標系下的地球自轉分量主要由緯度決定，表示為［13，18］

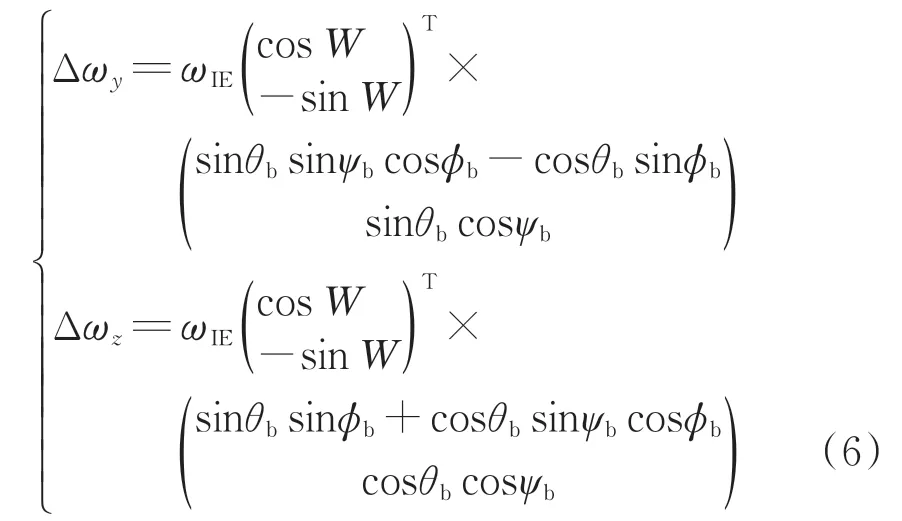
式中：W為緯度；ωIE為地球自轉角速度。

考慮上述誤差項，將式（5）和式（6）代入到式（4），可得

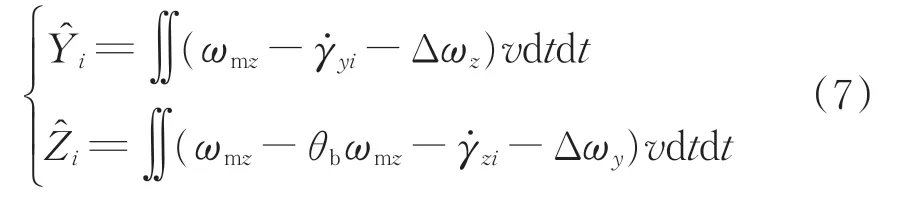
根據式（7）可對高低、軌向不平順進行測量，稱之為角速度測量法。一般來說，由長波不平順激勵的傳感器信號十分微弱，高精度的光纖陀螺儀可以提升測量精度。同時該算法通過構建基于“兩點弦”的測量模型，直接建立傳感器測量值與軌道不平順之間的聯系，因此在理論上不受傳感器敏感軸方向變化的影響，可提高系統的重復性精度。

2.3 測量效果

“兩點弦”測量模型與弦測法類似，都是采用在軌面上拉弦的方法，因此測量值相比真實值會發生形變。由于軌道不平順為隨機不平順，包含不同的波長成分，為研究算法在測量不同波長軌道不平順的幅值和相位變化，需要分析系統的傳遞函數。

由于高低與軌向不平順在角速度測量原理上的一致性，對二者統一分析。由圖2可知，角度ψ′與軌道不平順之間的關系為

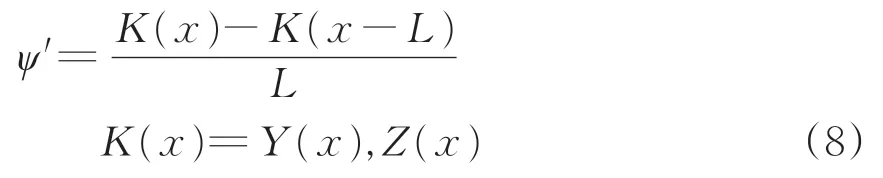
式中：K（x）為真實軌道不平順。

對式（8）進行傅里葉變換，得到角度ψ′與軌道不平順的傳遞函數H′(Ω)為

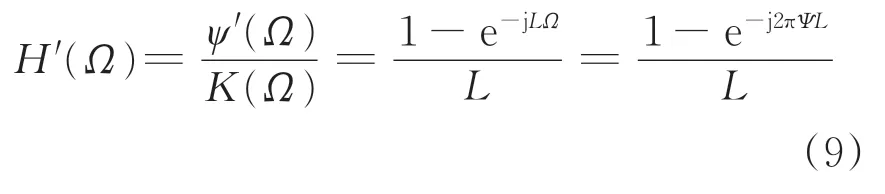
其中，

式中：Ψ為空間域頻率；Ω為時間域頻率；λ為波長。

將式（9）代入到式（4），得到角速度測量法的傳遞函數Hω(s)為

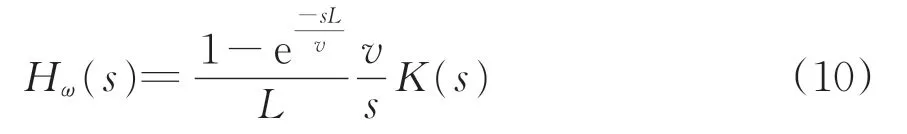
其中，

s=j2πΨv

式中：s為時域拉氏算符。

測量系統的幅頻特性曲線反映了測量結果與真實不平順之間的關系，根據式（12）得到角速度測量法的幅頻特性曲線如圖4所示。由圖4可以看出，該方法在測量0～20 m 區段的短波軌道不平順時存在明顯衰減，測量10～100 m 區段時存在非線性相位畸變，對整體測量精度影響較大，仍存在優化與改進的空間。

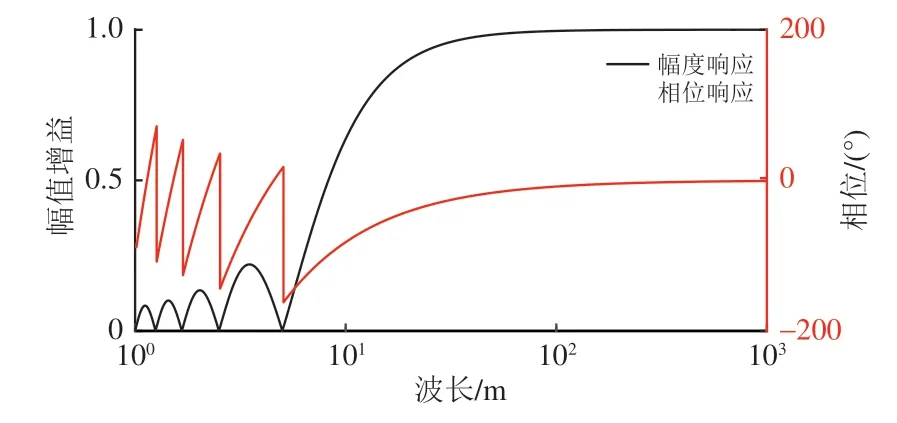
圖4 測量系統的幅頻特性

實際測量系統為離散系統，因此對傳遞函數作離散化處理。常用的離散方法有反向差分法、雙線性變換及脈沖響應不變法等［19］。其中反向差分變換法由于形式簡單在實際工程中應用廣泛，形式為

式中：T為采樣時間間隔。

將式（11）代入式（10），得到z域離散傳遞函數Hω(z)為

式中：系統固定空間采樣間隔Δx為0.25 m，前后測距組件縱向距離L為4.8 m。

設定M=LΔx?1，近似為整數20。那么離散測量系統可以近似為

其中，

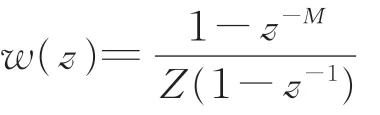
由式（13）可知，角速度測量法的測量結果相當于真實不平順經過形為矩形窗的低通濾波器。

傳統的加速度測量法通過對加速度計數據積分計算軌道不平順，因此在理論上計算結果直接反映軌道不平順。加速度測量法的傳遞函數Ha(z)表示為

2.4 互補濾波測量算法

為解決角速度測量法在測量短波軌道不平順時存在衰減的問題，引入互補濾波測量法。

從式（1）和式（4）可知，軌道不平順測量方法均需經過2 次積分計算。由系統隨機噪聲積分產生的低頻漂移及線路中的曲線和坡度等疊加形成無價值的趨勢項，常用高通濾波器法、擬合多項式法及小波變換法等將其消除［10］。軌道檢測系統采用窗函數法設計高通濾波器。

設計滿足截止頻率（或截止波長）要求的無限脈沖響應（FIR）低通濾波器，傳遞函數為F(z)，對應高通濾波器傳遞函數為1?F(z)［19］。級聯濾波器傳遞函數為F(z)和w(z)，對應高通濾波器傳遞函數為Γ(z)=1?w(z)F(z)。若系統采用傳遞函數為Γ(z)的濾波器去除低頻漂移，則測量結果與真實不平順的傳遞關系為

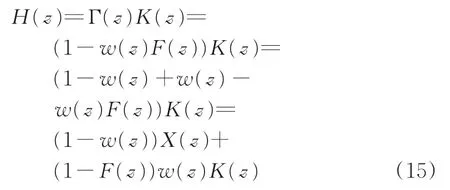
式中：H(z)為測量系統傳遞函數。

將式（13） 和式（14） 代入式（15），可簡化為

其中，

Fa(z)=1?w(z)

Fω(z)=1?F(z)

由式（16）可知，加速度測量法和角速度測量法的測量結果分別經過傳遞函數為Fa(z)和Fω(z)的2 個濾波器并累加，可計算出軌道不平順。本文將該方法稱為互補濾波測量法，2 個濾波器的組合形式為Γ(z)。

假設傳遞函數Γ(z)的截止波長為120 m，則傳遞函數Fa(z)，Fω(z)及Γ(z)的幅頻特性曲線如圖5所示。從圖5可以看出：傳遞函數Fω(z)與Γ(z)的幅度譜曲線相近，截止波長為63 m；傳遞函數Fa(z)的截止波長為6.6 m。

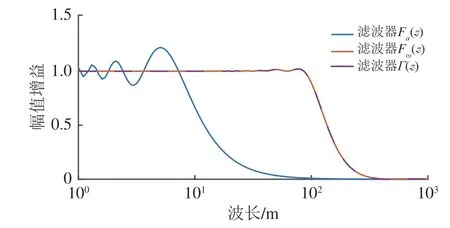
圖5 濾波器幅度譜對比

進一步，根據式（16）得到3 種方法的測量范圍如圖6所示。從圖6中可以看出：互補濾波測量法利用角速度測量法測量10～120 m 的中長波不平順，利用加速度測量法測量1.5～10 m 的短波不平順。

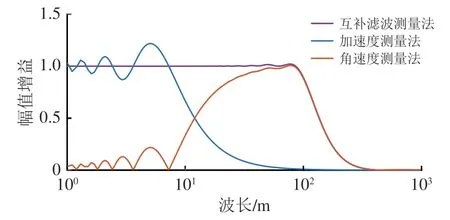
圖6 各算法測量范圍

在實際應用中，加速度測量法在測量短波不平順時精度較高。互補濾波測量法是利用加速度測量法的結果，對角速度測量法進行有效的補償。

高通濾波器Γ(z)（或長波濾波器）性能直接影響測量精度。采用多個矩形窗與三角窗級聯再并聯，設計得到本文所用的長波濾波器。對比新設計長波濾波器與GJ-5，GJ-6 型系統所用濾波器的幅頻特性如圖7所示。濾波器的性能指標一般有通帶抖動幅度和過渡帶寬，由圖7可以看出，該方法改善了GJ-6 型所采用長波濾波器的通帶抖動大小，過渡帶寬和阻帶截頻等基本保持不變。

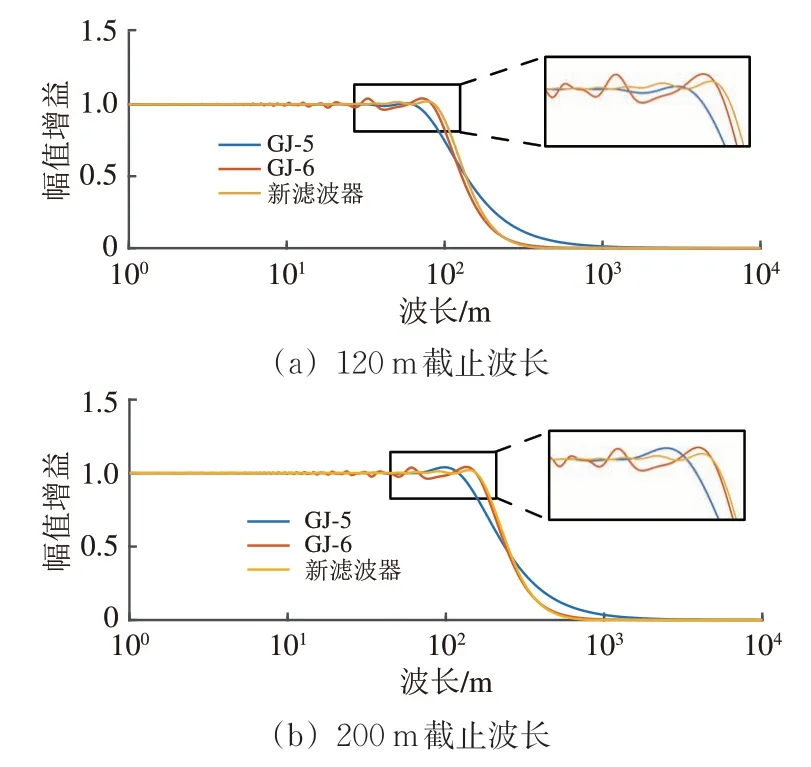
圖7 長波濾波器幅頻特性

在實際應用中，當軌道檢測系統速度低于40 km·h?1，加速度測量法結果變化劇烈、幅值較大，會降低互補濾波測量法的測量精度。因此，根據檢測速度選擇互補濾波測量法或角速度測量法，實現最高截止波長為200 m 的4 種不同波長的軌道不平順測量，算法流程如圖8所示。

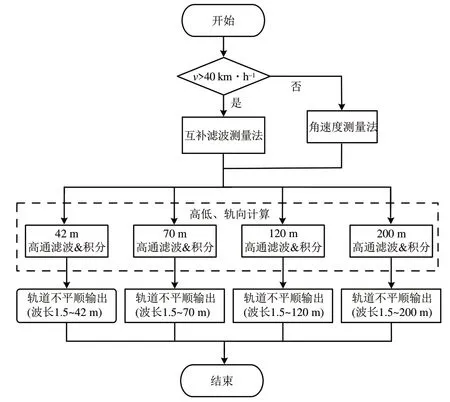
圖8 算法流程框圖

3 試驗與數據分析

為評估算法精度，同時避免傳感器采集和同步誤差帶來的影響，建立多體動力學模型，收集轉向架的振動響應和運動數據，將3 種算法計算結果與參考不平順對比，綜合分析檢測速度和傳感器噪聲系數對測量結果的影響。

3.1 多體動力學分析

整車建模時將車體、構架和輪對考慮為多剛體，車輛由1個車體、2 個構架、4個輪對及8個軸箱組成，共計62 個自由度。其中一系、二系減振器統一采用非線性彈簧阻尼元件代替，車體參數參考動檢車中較為普遍使用的CRH2C型列車，利用UM軟件搭建多體動力學整車模型如圖9所示［20］。

圖9 車輛-軌道耦合動力學模型（CRH2C）

取列車行駛速度為180 km·h?1，空間采樣間隔為0.25 m，模擬計算結果如圖10所示。從圖10可以看出：轉向架垂向位移與高低不平順較為接近，而橫向位移幅值比軌向不平順大；轉向架的搖頭角相比俯仰角幅值更小，低頻變化更為明顯。

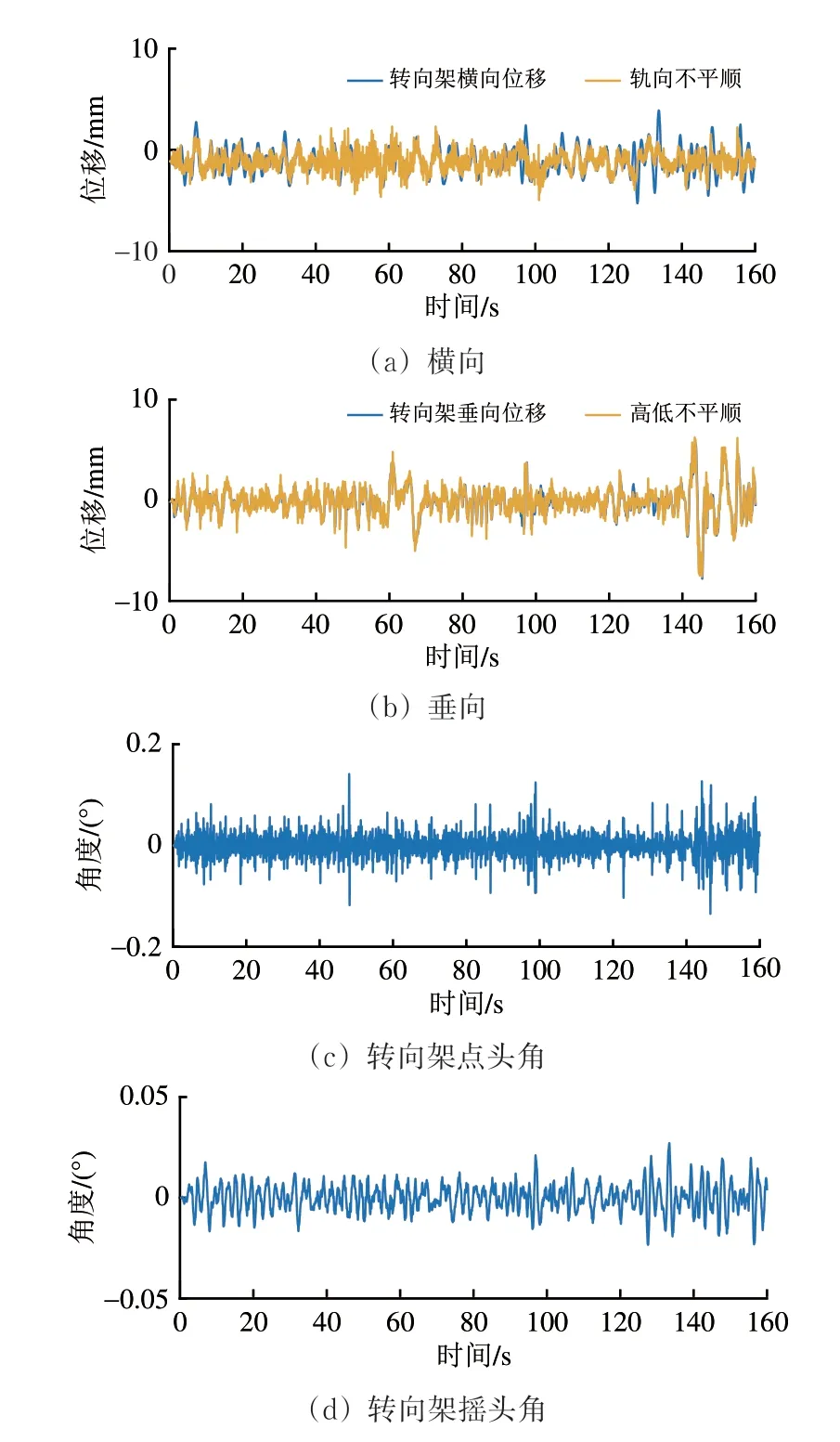
圖10 車輛-軌道耦合動力學仿真結果

3.2 傳感器噪聲建模

在測量過程中，IMU 的零偏在初始校準期間歸零，但會隨著時間增長產生漂移。這主要是因為溫度變化、電源電壓變化或材料老化等。目前評價光纖陀螺儀性能的主要指標為零偏穩定性，系統所采用的陀螺儀精度指標為1°·h?1（100 s平滑）。

Allan 方差分析法是常用的誤差分析法，可以綜合分析陀螺儀的性能，得到各項靜態誤差指標［22］。靜置光纖陀螺儀2～3 h 并采集數據，采用Allan 方差進行標定，得到零偏不穩定性為0.092°·h?1，速率隨機游走為0.39°·h?1.5，角度隨機游走為0.008 4°·h?0.5。其中零偏不穩定性和角速率隨機游走是引起陀螺儀長期漂移誤差和影響慣性測量系統性能的主要因素［21］，因此陀螺儀隨機誤差可建模成角度隨機游走和角速率隨機游走之和。設定陀螺儀隨機誤差為sm，表示為

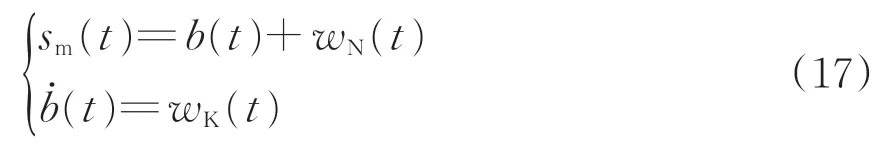
式中：wN和wK均為零均值的白噪聲，分別對應角度隨機游走和角速率隨機游走誤差；b（t）為噪聲wK的積分。

噪聲的自相關函數表示為

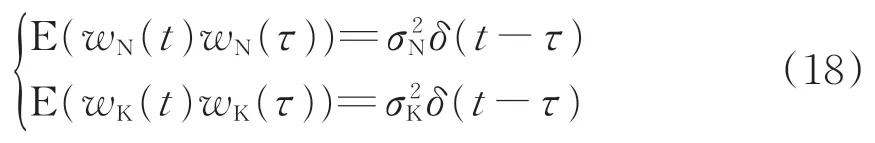
式中：E 為期望；σ2N為角度隨機游走白噪聲方差；σ2K為角速率隨機游走白噪聲方差。

對隨機誤差進行離散采樣，得到wN(k)和wK(k)，二者的方差分別表示為σ2NΔt?1和σ2KΔt，Δt為采樣時間間隔。對于加速度計，通常采用零均值白噪聲模型，方差記為σ2。

3.3 試驗結果對比

以某段高鐵線路綜合檢測車實測不平順數據作為動力學模型輸入，對收集的加速度和角速度等動力學響應加入隨機噪聲，分別用加速度測量法、角速度測量法及互補濾波測量法計算得到測量值。采用Welch法對試驗結果進行譜分析，段內傅里葉變換點數為4 096，加矩形窗，段與段間數據樣本重疊50%，試驗結果與功率譜密度幅值（PSD）曲線如圖11所示，圖中參考不平順為動力學模型的輸入不平順。

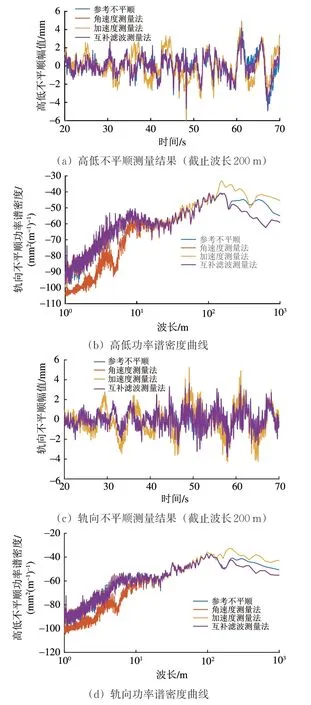
圖11 測量結果對比

從圖11可以看出：3種方法的結果與參考不平順波形相近，其中加速度測量法測量結果幅值略大于其他算法；角速度測量法測量結果在高頻部分（1～20 m）與參考不平順相比有明顯的衰減，在L處達到極小值，與理論分析一致；而加速度測量法在低頻部分（100 m 以上）有較大增益；相比之下，互補濾波測量法的PSD 曲線的低頻部分與角速度測量法一致，高頻部分經過互補濾波算法有效補償后，整體上最為接近參考不平順。

設定不同的檢測速度和噪聲系數，試驗條件見表1。表中噪聲系數為標定值，其中陀螺儀的速率隨機游走系數均為0.39°·h?1.5。選取長波濾波器的截止波長分別為120 和200 m，統計3 種算法測量結果的誤差絕對值均值（MAE）和均方根誤差（RMSE）見表2。由表2可以得出以下結論。

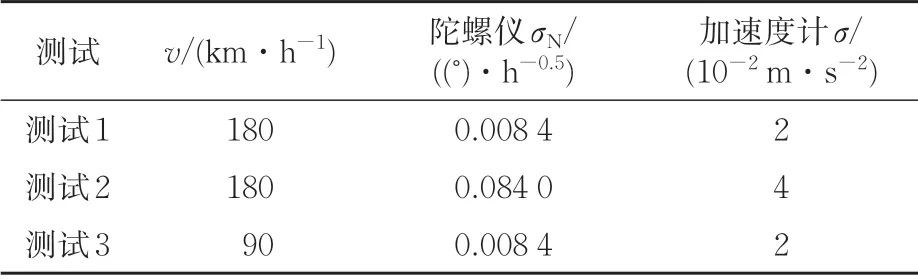
表1 試驗條件

表2 試驗結果 mm

（1）測試1 中，在高速下的角速度測量法與加速度測量法測量誤差接近，均有較高精度。當截止波長為200 m 時，互補濾波測量法精度更高，相對于加速度測量法，互補濾波測量法在測量高低和軌向不平順時平均精度分別提升24% 和58%，RMSE 分別降低0.10 和0.19 mm。在當前條件下互補濾波測量法的精度提升空間較小。

（2）測試2 相比測試1 增加了傳感器噪聲系數。當截止波長為200 m 時，加速度測量法的MAE 增加了1 倍，受噪聲系數影響明顯；角速度測量法和互補濾波測量法的測量精度基本不變。相比于加速度測量法，互補濾波測量法在測量高低和軌向不平順時平均精度分別提升59.5%和54.9%，RMSE 分別降低0.64 和0.45 mm。系統長時間服役后，傳感器精度會逐漸降低，此時互補濾波算法有較為明顯的優勢。

（3）測試3 相比測試1 降低了檢測速度。加速度測量法在低速下表現較差，MAE 增加了0.60～0.70 mm；而角速度測量法和互補濾波法的測量精度基本維持不變。相比于加速度測量法，互補濾波測量法測量高低和軌向不平順時平均精度分別提升73%和80%，RMSE 分別降低0.9 和1.0 mm。此外，對于互補濾波測量法，軌向比高低不平順的測量精度更高。從圖10可看出，這是因為轉向架在水平方向上比垂直方向變化較慢、且幅值較大。因此振動噪聲更小，傳感器信噪比更高。

選取綜合檢測車在某高鐵高速線路下實際采集的傳感器數據作為分析對象，對比加速度與角速度2 種測量方式在低速至停車條件下的高低不平順測量結果如圖12所示。

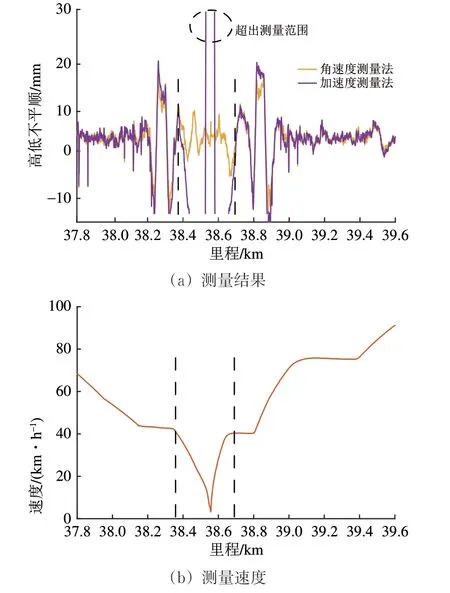
圖12 低速下軌道高低不平順測量

從圖12可以看出：當檢測速度在40 km·h?1以上時，角速度測量法與加速度測量法結果趨勢基本吻合；當列車以低速行駛直至停車時，加速度測量法測量的高低不平順產生了異常大值，而角速度測量結果始終在零基線附近，此時角速度測量法更能反映真實的軌道狀態。因此對于目前的檢測系統，根據速度選擇測量算法是有必要的。

綜上，互補濾波測量法可有效提升傳統加速度測量法的精度，尤其是在系統噪聲系數較大或低速檢測的條件下。在實際情況中，當列車在某條固定線路重復檢測或正反向檢測時，轉向架振動引起的加速度計敏感軸方向變化直接影響測量精度。互補濾波測量法則有效抑制了這一部分誤差。

此外，從算法執行效率來看，互補濾波測量法僅融合傳統測量法與角速度測量法，復雜度較低且各算法模塊之間耦合性較弱，滿足現有高速動檢車軌道檢測系統以350 km·h?1速度檢測的實時處理要求。

4 結 論

（1）通過在轉向架前后安裝測距傳感器，從而在軌道上構建了“兩點弦”，建立傳感器數據與軌道變化之間的對應關系，推導出角速度測量法，能夠避免傳感器敏感軸方向不規律變化對測量結果的影響。

（2）系統傳遞函數的幅頻特性表明，角速度測量法在測量短波軌道不平順時存在明顯衰減。互補濾波法可以有效利用傳統方法在測量短波不平順時的優勢，對角速度測量法進行補償。

（3）在測量長波軌道不平順時，檢測速度和傳感器噪聲系數對加速度測量法測量精度影響較大。由于光纖陀螺儀的低漂移特性，2 者對角速度測量法影響較小。在實測數據中，加速度測量法在低速檢測下精度較差，角速度測量法有明顯改善。

（4）數值仿真結果表明，相比于傳統算法，互補濾波測量法的測量精度可提升24%～80%。