基于變分模態分解高壓輸電線路故障測距分析

漣源市地方電力有限責任公司 黃自仁

輸電線路故障包括瞬時故障與永久故障兩類，針對前者可以利用自動重合閘或者繼電保護裝置，實現對于故障線路的切斷與保護。針對后者，如果重合閘切斷再閉合之后仍然無法恢復供電，就要等待維修人員找到故障地點進行人工修復。人工修復故障模式會受到很多外部因素的干擾，故障點定位效率較低，特別是長距離的高壓輸電線路出現故障，維修人員需要花費很長的時間才能確定故障點并進行維修工作。為了提升維修效率，需要使用更為先進的故障測距技術，幫助維修人員快速判斷故障點，降低線路故障所帶來的損失。

1 高壓輸電線路故障測距作用

利用高效的故障測距方式對高壓輸電線路故障進行檢測，一方面能夠幫助相關從業人員快速確定故障位置，避免由于故障長時間得不到處理而導致故障升級，或者由于故障處理不及時導致故障影響范圍擴大。同時，對高壓輸電線路故障測距技術進行升級，能夠減輕電力巡檢人員的工作壓力，針對永久性電力故障進行快速響應、快速處理，確保電力系統的穩定運行。另一方面，利用科學的故障測距技術，能夠幫助研究人員更為深入的研究高壓輸電線路故障理論，通過對理論的持續鉆研，提升測距結果的精確性，避免瞬時故障由于長時間得不到妥善處理，演化為永久性故障[1]。

2 變分模態分解基本原理

一旦高壓輸電線路出現了故障，在故障點會出現高頻暫態行波，這種狀態下，輸電線路的電流與電壓會將故障信息快速傳遞至輸電線路兩端，相關研究人員利用暫態行波非平穩、非線性的特點，基于變分模態分解理論，嘗試對暫態行波信息進行采樣、降噪、分解。利用變分模態分解方法，將暫態行波拆解為由若干個離散信號（uk）組成的信號。這種信號處理方式有別于傳統的EMD循環剝離信號處理方法，為高壓輸電線路故障測距提供全新思路。從整體上看，這種全新的信號分析模式主要分為三個步驟。

2.1 構建變分問題目標函數

第一，利用Hilbert變換技術獲取故障信號，并對信號進行分量處理，得到關于故障信號的單邊頻譜。第二，對故障信號的中心頻率進行解析，為每一個模態頻譜尋找與之相對應的“基帶”。第三，通過對分解信號（H1）進行高斯平滑處理得到帶寬。構建變分問題目標函數過程中，會遇到變分約束問題：

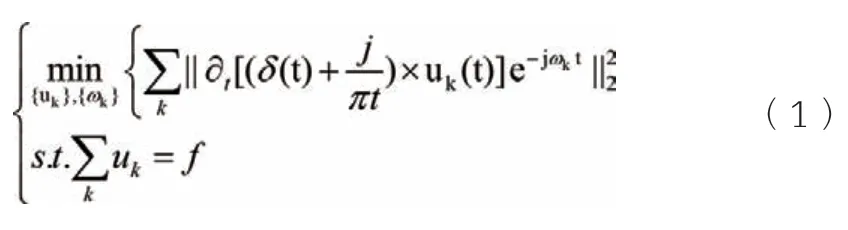
公式（1）中，{uk}={u1，…，uk}，以及{ωk} ={ω1，…，ωk}，分別表示函數集合以及中心頻率，δ（t）則代表脈沖函數。

2.2 設立二次懲罰項

在得到變分目標函數之后，引入二次懲罰項以及拉格朗日乘法算子，將該問題轉變為非約束性變分問題。由于拉格朗日乘子具有約束性，可以利用其約束性與二次懲罰項的收斂性，對拉格朗日公式進行擴充：

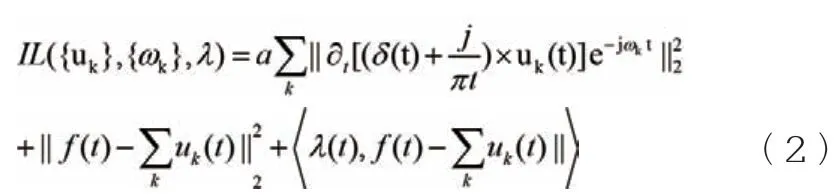
公式（2）中，λ（t）代表拉格朗日乘法算子，a為乘法因子，則為二次懲罰項[2]。

2.3 處理原始最小化問題

利用ADMM（交替方向乘子法）計算增廣拉格朗日函數鞍點，利用以及三項處理原始最小化問題，其計算公式為：

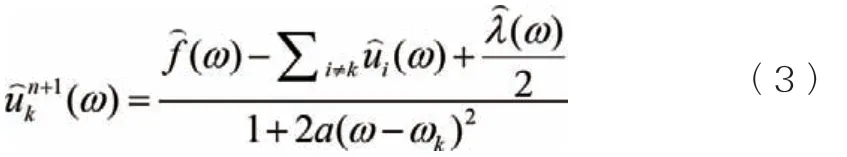
3 變分模態分析步驟

4 基于變分模態分解的高壓輸電線路故障測距仿真試驗

4.1 基于變分模態分解的故障測距方案

高壓輸電線路在實際工作中，會受到外界環境的影響，當線路出現故障，其故障信號中會夾雜大量噪聲。為了實現對于故障信號的有效提取，需要利用變分模態分解技術對故障信號中的噪聲進行過濾，其步驟如下：

第一，一旦高壓輸電線路某一點發生的故障，故障點會向輸電線路兩端傳輸電流信號與電壓信號，這些信號中含有大量高頻暫態分量信號，當電流信號與電壓信號傳輸至線路兩端之后，高頻暫態行波信號采集系統會自動讀取信號，并對信號進行收集與整理。第二，該系統對電流信號與電壓信號進行相模變換，通過這種方式得到高頻暫態行波的線模分量數據。第三，針對線模分量進行變分模態分解，得出每一種模態具體數據，通過這種方式過濾原始的高頻暫態行波信號中的噪聲。第四，利用數學形態濾波器，對每一個模態數據進行噪聲過濾，并對經過過濾的信號數據進行形態變換，利用柔性形態邊緣檢測技術，提取邊緣信號的特征信息，借助上述方式確定高頻暫態行波初始波頭達到系統端的精確時間。第五，將高壓輸電線路兩端得到的波頭到達時間導入公式（4），完成對于故障的測距工作。

公式（4）中，M、N為輸電線路兩個端點，dMf為故障點到M點的水平距離，L表示高壓輸電線路的水平長度，與表示故障點發出的高頻暫態行波信號到達M點、N點所花費的時間。使用公式（4）進行輸電線路故障測距的優勢在于該方式只考慮故障點與測量點（M、N）的水平距離以及信號傳輸時長，避免高頻暫態行波的波速與高壓輸電線路時間長度對于故障測距工作的干擾，提升故障測距的精準性[4]。

4.2 選擇仿真軟件

伴隨著供電壓力的逐步提升，供電網絡規模以及復雜性也在顯著增加，傳統的人工計算方式，已經無法應對例如潮流分布以及電壓降落等復雜的數據計算工作。因此，MATLAB、NETOMAC等電力系統計算/仿真軟件走入人們的視野，借助這些軟件大幅度提高電力系統計算效率。其中，NETOMAC軟件與常見的Windows操作系統適配程度較高，且高軟件的元件模型種類豐富，能夠仿真頻帶寬，在暫態計算、潮流計算、頻率響應等方面擁有出色的處理能力。

此外，該軟件的開放程度較高，用戶可以根據自己的實際需求，對軟件中的參數進行自定義設定，還可以自由嵌入各類數學計算公式以及子語言程序。MATLAB軟件的優勢在于數據計算能力出眾，且數據輸出語言表述較為簡單，適合初學者快速上手、使用。該系統中內嵌的Simulink仿真工具為該系統搭建了優秀的數據分析環境。工作人員只需要使用Power system工具，就可以在MATLAB系統上搭建電力系統仿真模型，對電力系統的暫態穩定性進行觀察與研究。利用該軟件強大的分析能力，進行時域仿真判斷以及人工智能判斷。針對電力系統的故障分析，就是建立在時域分析法之上，依據不同的電力元器件模型之間的拓撲關系，構建完整的電力系統模型，利用微分方程以及代數方式，實現對于高頻暫態行波數據的快速處理。

本次仿真試驗中，相關工作人員利用NETOMAC軟件對220kV輸電線路故障進行仿真試驗，將仿真數據代入MATLAB軟件，完成輸電線路故障測距工作。

4.3 輸電線路仿真模型

工作人員使用NETOMAC軟件構建220kV輸電線路仿真模型（如圖1所示）。

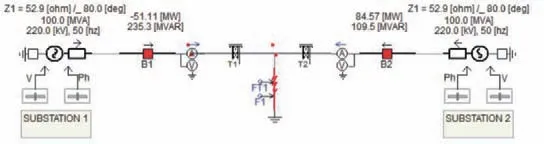
圖1 220kV輸電線路仿真模型

分析圖1可以發現，該仿真模型中用到了Bergeron、PI以及Phase三種常見的輸電線路模型，工作人員需要將電阻、電容等參數代入PI模型，在代入參數過程中可以忽視輸電線埋深參數，縮減模型數據體積。本次試驗使用的Bergeron模型是一種沿著輸電線路均勻分布參數模型，即便高壓輸電線路的高頻暫態行波頻率范圍較大，Bergeron模型也能夠完成數據處理工作。

4.4 兩端信號分析

本次仿真試驗選擇的220 kV輸電線路全長200km，將采樣頻率設定為1MHz，端點設為M，四個故障點與M點的距離分別為70km、100km、140km以及180km，在0.2S時發生故障，系統截取故障發生后3ms數據進行分析。通過模擬不同故障距離中涵蓋的多種故障類型，驗證基于變分模態分解的故障測距有效性。工作人員設定距離M點30km處發生了A相接地短路故障（如圖2所示）。

分析圖2可以發現，當該輸電線路發生接地短路故障之后，A相暫態電壓發生了大幅度變化，其余兩相并沒有發生明顯變化。工作人員截取故障發生后一段時間內的故障數據，為了在仿真實驗中模擬真實故障常見，對故障數據進行人為加噪，由于三項輸電線路之間電場與磁場具有耦合性，因此要對截取的數據進行Clarke變換，得到行波獨立線模分量[5]。

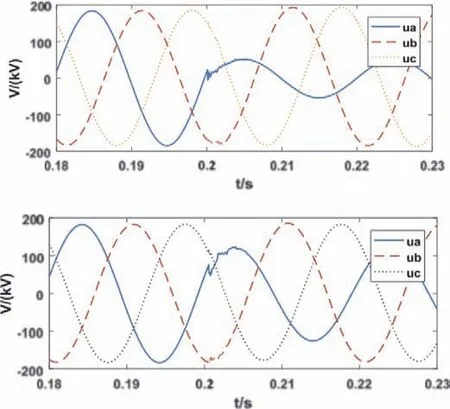
圖2 M、N側三相電壓行波波形示意圖

表1 不同故障測距結果

變分模態分解的結果與懲罰因子（α）以及因子分解個數（K）有關，當α值與K值發生變化，分量信號也會隨之改變。本次仿真試驗中，工作人員將K值設定為3與4，觀察不同的K值計算得出的分解分量是否符合計算要求。同時，工作人員將α的參數設定為500/1000/1500/3000，得到不同的分量瞬時頻率均值，之后再將α調整至2000，對各組分量瞬時頻率均值進行橫向對比。通過對比可以發現，當K=4時，分量瞬時頻率均值的扭曲較為明顯，均值扭曲情況與分解個數呈正比關系。為了避免均值扭曲，工作人員將K值確定為3，此時分量瞬時頻率均值的扭曲情況明顯緩解，且α=2000時，均值圖像更為平滑。

4.5 故障距離檢測

工作人員在仿真系統中設定了不同的故障類型，觀察每一種故障類型在四個故障位置上的仿真數據（見表1）。

觀察表1數據可以發現，基于變分模態分解的輸電線路故障測距，無論是什么故障類型，都能夠精準進行故障測距，故障精度達到了1%，且故障測距誤差在+0.524～0.201，處于誤差允許范圍之內。由此可以證明，利用變分模態分解技術能夠快速進行故障測距工作。

5 結語

高壓輸電線路運行環境復雜，線路跨度大，如何快速尋找高壓輸電線路故障點，一直以來都是電力工作人員重點關注的問題。電力從業者基于變分模態數據分析技術，嘗試對輸電線路故障測距方式進行優化，利用變分模態技術實現對不同類型故障的快速測距。同時，通過仿真試驗，證明該方法的有效性，為電力運維工作提供技術支撐。