一種結合策略價值網絡的五子棋自博弈方法研究

劉 溜，張小川，彭麗蓉，田 震，萬家強，任 越

(1.重慶理工大學 兩江人工智能學院, 重慶 401135; 2.重慶理工大學 人工智能系統研究所, 重慶 400054;3.重慶工業職業技術學院 人工智能與大數據學院, 重慶 401120;4.重慶市南開兩江中學校, 重慶 401135)

0 引言

在人工智能的發展歷程中，人們一直嘗試賦予計算機“思考”的能力。為此，科學家嘗試通過給計算機編程、設計博弈系統、運行棋類博弈游戲，期望實現計算機模仿人類下棋[1]。那么，如何構建計算機博弈系統呢？首先，設計合適的數據結構，以表達棋局局面信息；其次，數字化規則，設計合法的落子著法；最后，構造一個全局性的博弈策略，以期發現能使己方收益最大化的著法。

計算機博弈系統可以通過構造博弈樹來完成博弈行為。19世紀50年代，香農提出了計算機博弈的核心思想：通過構建完整的博弈樹，搜索當前局面的最佳著法[2]。但在實際博弈過程中，卻難以構造一顆理想的博弈樹。主要原因是對于博弈中的某個局面，可行的著法數通常較大，而且隨著博弈進程推進，這個數字還會呈指數級增加。而發現能決定勝負的著法，理論上來講，最好就是窮盡所有可行著法。在強實時、高對抗的博弈進程中，計算資源的有限性決定了窮舉法基本是不可能的方法。

傳統蒙特卡洛樹搜索摒棄窮舉思想，結合了模擬采樣的隨機性和樹搜索的準確性，對各分支的探索權重進行評估，使計算資源集中在重要分支上。但此算法采用隨機走子策略模擬對局，在沒有被訪問足夠多的次數的情況下，不能夠對關鍵樹節點進行可靠評估。導致此算法效率很低，一定時間內即使是在中等復雜度的博弈中也難以給出優質決策。

為了克服上述缺點，本文提出通過結合深度神經網絡改進蒙特卡洛樹搜索算法，設計了一種五子棋計算機博弈深度強化學習算法；其中，通過神經網絡擬合局面評估函數和落子概率分布的方法，引導蒙特卡洛樹搜索方向，提升搜索速度；同時，基于自博弈強化學習訓練框架，實現了神經網絡的迭代優化，加強搜索強度。

1 傳統蒙特卡洛樹搜索

蒙特卡洛是一種統計實驗方法，利用事件發生頻率近似事件發生概率。蒙特卡洛樹搜索通過蒙特卡洛方法逐步遍歷和擴展博弈樹：樹中節點的遍歷是基于對局面估值的貪心利用；樹外節點的擴展則是通過隨機策略進行多次快速走子模擬，用勝負結果近似局面評估[3]。如圖1所示，蒙特卡洛樹搜索算法共有4個步驟：選擇、擴展、模擬、回溯。

圖1 蒙特卡洛樹搜索的四步圖

步驟1選擇：以當前局面為根節點，完成從根節點到達葉子節點之間的路徑選擇。通過引入上限置信區間算法(UCB)，進行節點選擇的同時考慮平衡探索次數和局面估值[4]。

(1)

式中：Vn為節點估值，Tn為節點探索次數，C為平衡因子，C越大則越偏向探索次數少的節點，反之則偏向局面價值高的已探索節點。

步驟2擴展：當到達某個未被探索過的葉子節點時，列舉其下所有可行著法。否則進入模擬階段。

步驟3模擬：采用隨機策略，模擬雙方對弈直到游戲結束產生勝負結果。

步驟4回溯：將勝負結果從葉子節點層層向上回溯到根節點，更新途經節點的探索次數以及估值。

2 結合神經網絡的蒙特卡洛樹搜索

結合深度神經網絡和蒙特卡洛樹搜索，提出一種自博弈學習方式，從零開始學習五子棋。

2.1 策略價值網絡生成棋局著法

人類博弈時，首先需評估局面預測己方勝負，其次選擇有利落子。本文模擬人類思考過程，構建策略價值網絡返回可行落子概率以及局面評分。

2.1.1策略價值網絡的輸入特征及結構設計

局面表示是計算機理解博弈過程的先決條件。在深度學習理論中，這一步也被稱為特征提取。有學者將人類知識融入特征提取中，比如DeepMind曾融入圍棋中“氣”“征子”等概念，幫助AlphaGo理解圍棋[5]，卻最后掣肘了AlphaGo棋力提升。

提取了落子分布以及決策方信息。如圖2所示，使用矩陣表示棋盤，用1代表此位置已有落子，0表示暫無落子，全1或者全0的棋盤代表此時輪到執黑方或執白方落子。

圖2 棋局信息表示實例

網絡起始為3層公共卷積網絡，分別使用32、64、128個3×3的卷積核，均使用ReLU激活函數，如圖3所示。隨后分成policy和value 2個輸出：policy輸出端，先用4個1×1的卷積核降維，緊接一個全連接層，最終使用softmax函數輸出棋盤上每個位置的落子概率；value輸出端，先用2個1×1的卷積核進行降維，再連續接2個全連接層，最后使用tanh函數輸出[-1，1]之間的局面評分。

圖3 策略價值網絡結構設計框圖

2.1.2策略價值網絡的損失函數

策略價值網絡的輸入是棋局描述s，輸出是落子概率估計p以及勝負估計v。自博弈的過程中，會探索各種局面s、實際落子概率π以及勝負結果z，收集(s,π,z)數據用于后面的網絡更新。訓練目標是讓策略價值網絡輸出的p和v更加接近經過蒙特卡洛樹搜索采樣模擬后得到的π和z[6]。如式(2)所示，本文將聯合損失作為該網絡優化的目標函數。

lv-z代表局面勝負估計v和實際蒙特卡洛樹搜索返回值z的均方誤差，根據策略梯度下降算法，需要最小化目標策略的評估函數J(πθ)的相反數-J(πθ)，即p和π的交叉熵誤差，其中θ表示策略價值網絡參數。

l=lv-z-J(πθ)=(z-v)2-πTlogp

(2)

為了緩解網絡過擬合的問題，考慮引入正則化。引起過擬合的主要原因在于模型復雜，參數過多而正則化的基本思想是引入懲罰項以減少參數量級。

最終的損失函數為：

(3)

2.2 自博弈中蒙特卡洛樹搜索提升著法策略

人類通過推演落子后的棋局變化評估落子價值。而蒙特卡洛樹搜索可憑借強大的采樣能力，用模擬統計結果近似落子概率，達到棋局推演的目的。如圖4所示，可以將蒙特卡洛樹搜索作為一個策略提升器，校準策略價值網絡輸出的落子概率。

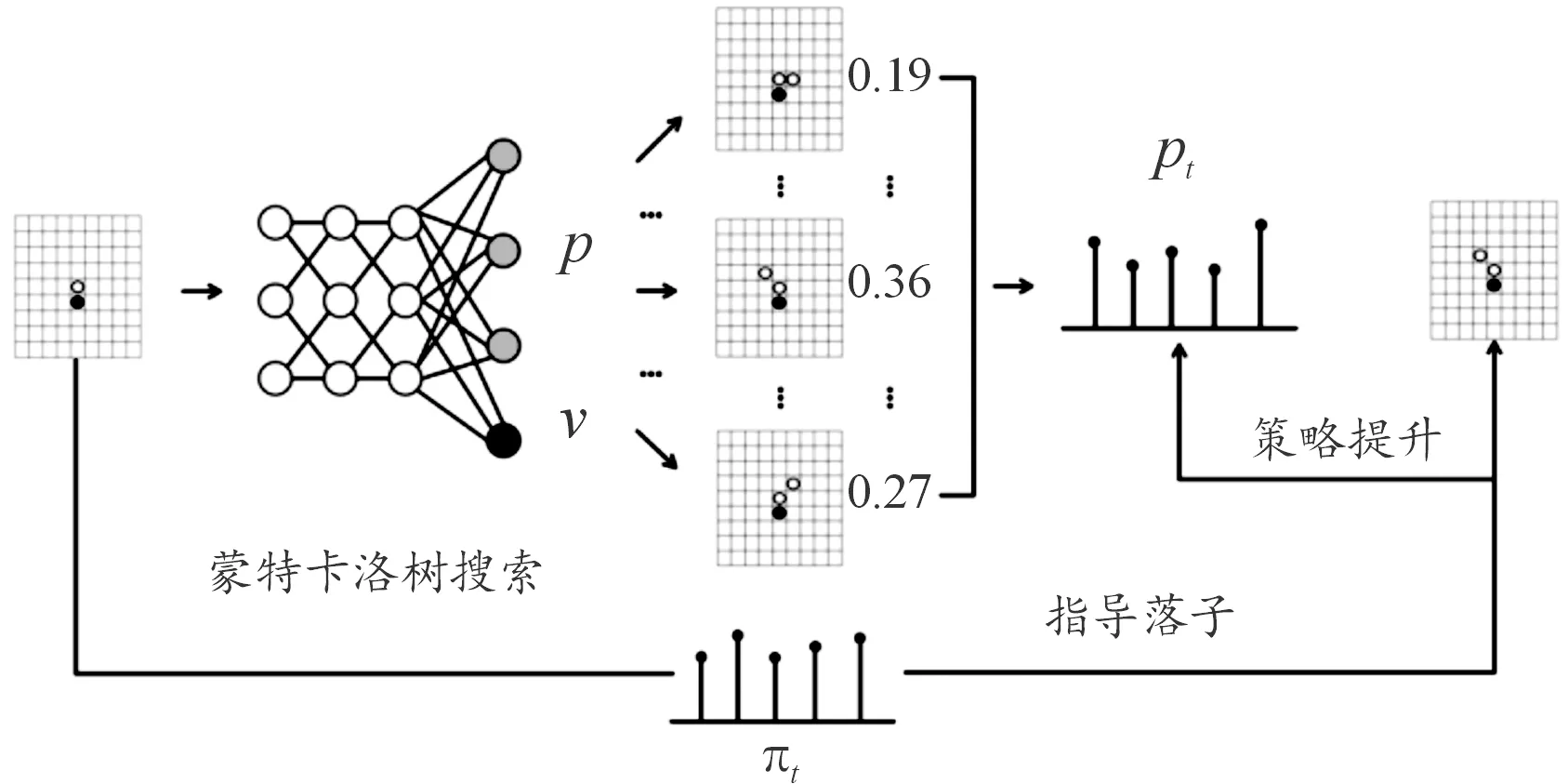
圖4 策略提升器—蒙特卡洛樹搜索圖

一局完整的自博弈，從某一棋盤狀態s1，經歷s2，s3，…一直到結束狀態sT。每一個st下，都會執行一次完整的蒙特卡洛樹搜索，搜索過程中使用策略價值網絡進行輔助，最終返回st下不同位置的落子概率πt，自博弈的真實走棋根據落子策略πt決定。到達sT后，得到這一局結果z，一般是-1、0、1之一，分別對應輸、平和贏。對于自博弈的每一步，都要保存一個三元組(st，πt,zt)作為一個訓練樣本。自博弈中最關鍵的一步就是在st下，如何執行蒙特卡洛樹搜索，并返回不同位置的落子概率。改進的蒙特卡洛樹搜索具體分為以下3個階段：選擇階段、擴展模擬階段、回溯階段。通過反復執行這3個步驟，逐漸建立一棵樹，然后根據樹中存儲的統計信息得到落子的概率分布。

搜索樹中的節點記錄棋局狀態，節點訪問次數N(s,a)表示在狀態s下采取著a法的頻率；累計行動價值W(s,a)表示(s,a)局面動作在采樣模擬中獲得的總收益；平均行動價值Q(s,a)是W(s,a)與N(s,a)的比值；先驗概率P(s,a)由策略價值網絡給出，表示對落子概率的估計[7]。

2.2.1節點選擇

節點選擇是指從合法動作集中選擇一個著法。關于節點選擇策略，受UCB式(1)的啟發，設置變量U(s,a)用以平衡節點的探索和利用。

(4)

式(4)包括兩部分：Q(s,a)代表著法a在s下獲得的平均價值，是對局面評分貪心利用；P(s,a)是策略價值網絡給的著法指導；公式最右邊是計算在s下選擇a的頻率比重；cquct是超參數，用來調整探索和利用的比例。策略開始會偏向選擇次數少的節點，這是對探索的鼓勵避免錯過價值高的著法，隨著模擬次數越來越多，策略會偏向那些Q(s,a)高的節點，將計算資源集中在最佳探索分支上。

2.2.2節點擴展和模擬

依據節點選擇策略，不斷進行樹內節點選擇，直到遇到一個從未探索過的葉子節點sl。如果sl是終止節點則直接進入節點回溯階段，否則需要將sl下所有的分支節點添加到搜索樹中，并分別保存采取落子動作后進入的新局面。

同時策略價值網絡會給出sl下的每個合法落子概率pl以及局面評分vl，pl存儲在sl到各個分支節點的邊中。由于各分支節點都是新加入到搜索樹中，需要將對應邊中的其他變量N(s,b),W(s,b),Q(s,b)均作初始化處理，隨后進行隨機模擬直到游戲結束。

2.2.3節點回溯

此階段完成從葉子節點sl到根節點s0路徑上的參數更新。這是蒙特卡洛樹搜索能集中計算資源于重要分支的原因。假設sl的父節點為st,st到sl之間的落子動作為dt，策略價值網絡給sl的評分為vt。則從sl回溯到st的參數更新如式(5)—(7)所示。

如果sl是終止節點，vt將不會使用策略價值網絡給出的勝率評分值，直接使用勝負結果值：-1、0、1之一；在回溯的過程中，每經過一個節點，vt值要進行取反操作，因為博弈樹中模擬的是雙方博弈的過程，一方的收益對于另外一方則是損失。

W(st,dt)=E(st,dt)+vt

(5)

N(st,dt)=N(st,dt)+1

(6)

(7)

2.2.4實際落子選擇

將當前局面視為搜索樹的根節點s0，經過選擇、擴展和模擬、回溯，結束一次蒙特卡洛樹搜索。而每一次真實落子需要根據經過多次蒙特卡洛樹搜索，這也是自博弈特別消耗計算資源的原因。多次采樣之后，根節點s0下所有邊存儲的信息都得到了更新，利用這些信息可以計算s0下的落子概率。如式(8)所示，在s0下采取落子動作a的概率為：

(8)

受模擬退火算法的啟發，設置溫度參數τ控制蒙特卡洛樹搜索收斂到重要分支。最開始τ設置為1，此時落子概率分布較均勻，偏向選擇訪問次數少的落子動作；隨著自博弈持續進行，τ值逐漸減小為0，此時訪問次數多的落子更加容易被選擇。最后選擇π(a|s0)最大的對應著法a當作實際落子動作。

3 算法性能對比實驗

3.1 實驗環境

本實驗平臺為Windows 10，運行內存為 8.0 GB，顯卡配置為NVIDIA GeForce GTX 1050Ti，主體代碼使用python語言實現，神經網絡搭建使用pytorch深度學習開發框架。

3.2 實驗對照算法

為了使實驗結果更加可信，本文引入另外2種經典搜索算法用作效果對照。

極大極小值是一種適用雙人零和博弈的搜索思想。核心是分別站在各博弈方進行搜索，其中一方在可行著法中選擇自身利益最大化的落子著法，而對方就要盡可能阻止對方選擇該最佳落子[8]。一般極大極小值算法需要通過構造一個局面評估函數，計算出對己方最大、對方最小的著法。分析發現，局面評估函數常常與棋子數、棋子分布及其關鍵棋型3個因素密切相關[9]。本文設計局面評估函數時，先嘗試對不同棋型賦予一個先驗權值，再根據棋子位置，賦予另一個先驗值[10]。式(8)中x,y,z分別表示處于棋盤上“核”“邊”“角”位置上雙方棋子數目之差，而N1、N2、N3分別表示“活四”“沖四”“活三”3種關鍵棋型數目，如圖5所示。

圖5 五子棋重要棋型以及位置分布示意圖

f(x,y,z,Ni=1,2,3)=3x+2y+z+100N1+50N2+20N3

(9)

Alpha-Beta剪枝算法本質上是一種對極大極小值算法的優化。其核心思想是記錄中間節點Min的最小值α，節點Max的最大值β及其局面估計值Value，以達到對搜索樹裁剪的目的[11]。在Alpha-Beta算法中，通常將對Max節點層的剪枝稱為Alpha剪枝，對Min層的裁剪稱為Beta剪枝。如圖6所示，無論采用哪種剪枝，其核心都是需要比較兄弟節點Value值、父節點α值或者β值。

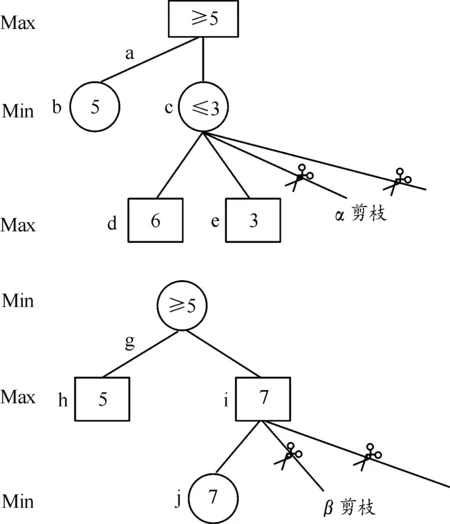
圖6 Alpha-Beta剪枝過程示意圖

從理論上講，在棋盤中任意一個空白位置都是合理的落子選擇點。但是，在五子棋博弈中，落子會相對集中于某個區域，因此，區域內的搜索價值更大。為此，本文引入變尺度思想，將棋盤離散化不同價值區域，對不同區域再賦予Alpha-Beta剪枝搜索的不同深度值。

本文用搜索效率和博弈水平2個標準，綜合比較了極大極小值搜索，Alpha-Beta剪枝，傳統蒙特以及改進蒙特卡洛樹搜索4種算法的性能[12]。表1展示了實驗中用到的具體算法類型及重要參數。

同時本文為了驗證搜索空間大小對搜索算法的影響，分別設計9×9、11×11、15×15三種尺寸的棋盤，作為驗證環境。

表1 算法類型及重要參數

3.3 搜索效率對比

構建和遍歷一棵搜索樹所耗費的時間即平均落子時間，是體現算法搜索效率的重要指標[13-14]。如圖7所示，各算法在不同棋盤上，平均落子時間隨對弈步數的變化情況。

相較于經典搜索算法，改進后的蒙特卡洛樹搜索在搜索效率上有了大幅度的提升，平均落子時間僅僅只有極大極小值算法的1/196，Alpha-Beta剪枝算法的1/55，傳統蒙特卡洛樹搜索的1/28。此外這種改進算法在不同大小的棋盤下的落子決策時間無明顯變化，說明其具有相當的魯棒性。

圖7 各算法在不同棋盤上平均落子時間隨對弈步數的變化曲線

3.4 博弈水平對比

為了比較各算法間的博弈水平，設計五子棋對局實驗。實驗中任意2種算法之間均設置100局比賽，統計各算法的勝負平數據，結果如圖8所示。對局實驗中采用的是比賽標準15×15的棋盤。

當極大極小值算法并未使用局面評估函數，而是將博弈樹完全展開至游戲結束。與其他經典搜索算法相比，對局平均不敗率達到了97%，但是勝率卻僅有約36%。這是由于極大極小值算法的核心是以避免對手獲取最大收益，而不是以自己取勝為目標。

圖8 算法間對局實驗結果統計

對于Alpha-Beta剪枝算法，實驗設置兩組搜索深度用于對照，結果顯示淺加搜索深度并不能顯著提高搜索水平。與其他經典搜索算法相比，搜索深度加1，勝率僅僅提高了2%。因為基于人類經驗設計的評估函數，并不能保證對每一個局面的評估都來源于真實的勝負反饋。對弈越早期，這種評估上的誤差就越大，而且誤差還帶有積累效應。

在傳統蒙特卡洛樹搜索的對局中，為了驗證模擬次數對其搜索水平的影響，實驗設置1 000次，2 000次，3 000次3組參數。通過觀察實驗結果，發現模擬次數的增加同樣不能顯著提高其搜索水平。模擬次數增加1 000次，平均勝率增加不到1%，甚至出現增加模擬次數但是勝率反而下降的情況。一定程度上說明了模擬中采用隨機落子策略，缺乏先驗指導很難收斂到重要分支。

改進的蒙特卡洛樹搜索在勝率上均取得了明顯的優勢。實驗結果顯示，與極大極小值算法、Alpha-Beta剪枝算法、傳統蒙特卡洛樹搜索算法相比，平均勝率分別達到了75%、84%、87%。

4 結論

以五子棋為研究載體，分析了經典的蒙特卡洛搜索算法的缺點。針對這些缺點，設計出一種結合策略價值網絡的蒙特卡洛樹搜索，以深度神經網絡擬合局面評估函數，用先驗落子概率指導蒙特卡洛搜索，形成一種先驗知識支持的自博弈方法。與傳統的搜索算法相比，改進后的方法無論是在搜索效率，還是博弈水平上，都有較大程度的提高。