智能搜救艇航行安全分析

舒 展，高 慧，林玉璋，劉森林

（天海融合防務裝備技術股份有限公司，上海 201612）

0 引言

海面上發生船舶遇險損毀事故時，需要在現場應用特種救生救助裝備開展海上救助作業。而在高海況下，有人駕駛的搜救船舶難于開展正常作業。無人搜救艇開展海上救生救助是安全可靠的選擇，但由于該搜救作業在高海況下開展，無人艇在高海況中的瞬時運動及安全問題需要進行分析研究。本文就此安全問題進行數值模擬和計算分析，評估其作業安全性。

1 智能搜救艇概況

智能無人搜救艇船型參數如下，艇總長Loa＝6.25 m，型寬B＝2.15 m，型深D＝1.265 m，吃水d＝0.607 m，排水量Δ=2.863 t，浸濕面積S=10.8 m2。具體主尺度見表1。基于型線圖和型值表，艇體三維建模見圖1。

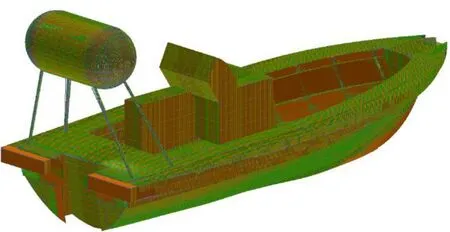
圖1 3D 模型圖

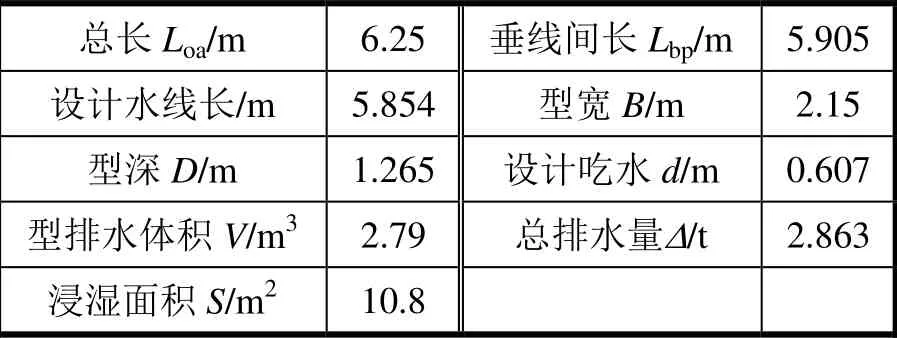
表1 無人搜救艇船體參數表

2 技術思路

由于智能無人搜救艇在高海況下進行作業，高海況下的運動響應是典型的強非線性水動力學問題，傳統的勢流方法對這種強非線性的艇體和波浪相互作用勛在局限性。因此需要借助計算流體力學手段開展直接數值模擬。綜合應用基于靜力學的靜水和波浪中穩性計算評估，和基于動力學的頻域勢流、時域黏流耐波性計算評估。首先，對穩性計算評估，基于靜力學方法計算最不利工況下的艇體橫搖復原力臂，評估艇體在靜水和波浪中的穩性。其次，對耐波性計算評估，先基于傳統的頻域勢流切片法預報艇體運動響應幅值算子和6級海況下的運動譜，根據頻域結果搜索最不利的波浪環境，確定時域計算波浪參數和工況；再基于時域黏流的計算流體力學方法，建立數值波浪水池模擬強非線性海面波浪環境、艇體運動方程，并在時域計算分析艇體運動響應。最終通過靜力學和動力學方法，分析無人搜救艇在高海況下的穩性、耐波性，評估航行安全性能。

3 智能搜救艇穩性分析

無人搜救艇吃水d=0.6 m，排水量Δ=2.86 t，重心高度0.66 m。滿載吃水下，計算靜水和波浪環境下的初穩性高、穩性復原力臂，最后根據法規要求評估其穩性，同時評估其自扶正功能[1]。圖2為艇體模型圖。

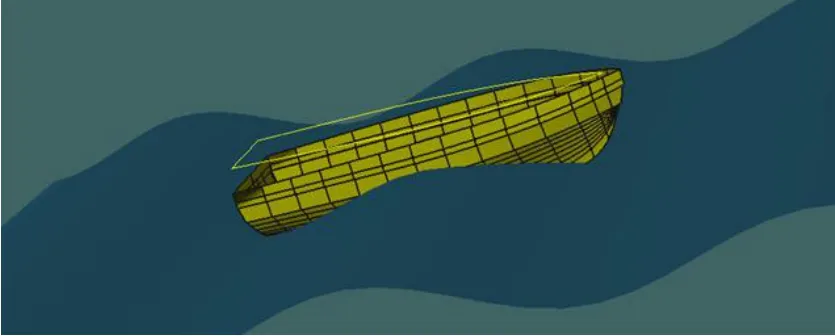
圖2 艇體模型圖

此智能搜救艇體需在高海況下作業，由于風浪聯合作用，艇體受到外力干擾，使其產生傾斜，這樣就破壞原來正浮時的平衡狀態，外力消失，船體由傾斜狀態自動恢復至平衡狀態，這樣的能力為船舶具有足夠穩性[2]。艇體在波浪中具有參數橫搖特性，考慮艇體處于波峰位于船中、波長等于船長的迎浪情況，相對于靜水正浮狀態，此時船體水線面損失最大，容易發生波浪中失穩得最不利狀態。考慮波長為船長6.25 m，在極限波陡為八分之一的條件下，波高取為0.78 m，波峰位于船中，此時艇體強制橫搖180°，計算波浪中不同橫搖角度的穩性力臂值，分析其穩性特征。

圖3為智能無人搜救艇在0～180°橫傾下的復原力臂圖。表2為穩性力臂表。

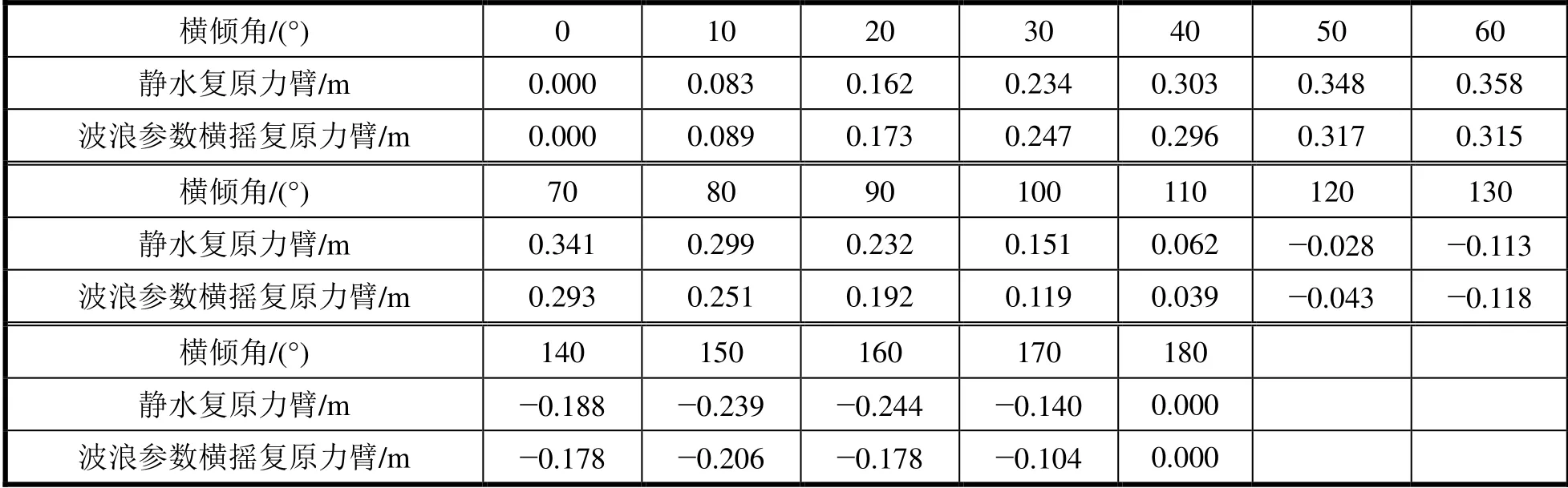
表2 穩性力臂表

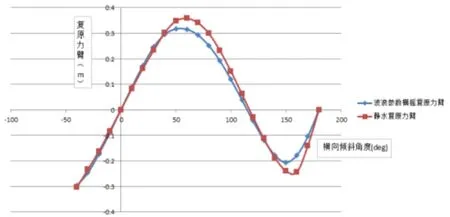
圖3 復原力臂圖

由計算結果可知，在靜水、波；浪環境中無人搜救艇，初穩性高為0.461 m，最大復原力臂對應角為54.5度，最大復原力臂值為0.319 m；在0～180°傾斜角度范圍內，除了初始狀態為平衡位置，在116.9°也為平衡位置，即船體傾斜到～114°，船體復原力臂為0，在此狀態，若稍給外力矩，則艇體會快速自動復原至正浮狀態，此能力稱之為具有自扶正功能。

根據法規對穩性的要求：1）初穩性應不小于0.15 m；2）橫傾角30度處的復原力臂應不小于0.02 m；3）船舶最大復原力臂所對應的橫傾角應不小于30°[3]。由靜水穩性計算結果對比，可知智能無人搜救艇靜水及波浪中穩性滿足規則要求。

4 耐波性計算工況搜索

計算海況為六級海況，對應有義波高為6.0 m、波譜峰周期為9.993 s，選用JONSWA波浪譜。無人搜救艇以4.0 kn的航速航行。

為分析無人搜救艇在6級海況下的艇體運動響應特征和安全性能，首先需要快速的評估分析其在各種浪向下的運動特性。選用經典的有航速艇體運動響應預報的頻域切片方法，考慮90°、120°、150°和180°等4種浪向，快速預報4 kn航速艇體的運動響應幅值算子（Response Amplitude Operator，RAO）、給定海況下的艇體運動譜，獲得六級海況下各波浪頻率成分對應的艇體運動幅值和峰值頻率。相應的計算工況參數見表3。

表3 無人搜救艇頻域計算工況參數

但以上分析在線性頻域內實現的，并沒有考慮到高海況實際波面的完全非線性特征，還需要開展時域非線性波浪環境的波面模擬和艇體運動響應計算分析。

因此，結合無人搜救艇以迎浪航行時最為不安全的實際情況，確定時域計算工況的非線性波浪參數。具體為：浪向為180°迎浪，波浪遭遇頻率選取縱搖垂蕩運動譜峰值頻率、縱搖固有頻率和波長等于船長的波頻3個極端頻率點，作為時域計算工況。具體參數列表如下，其中縱搖垂蕩運動譜峰值頻率0.81 rad/s的計算工況Case-T3，其波長達140 m，對6.25 m長的無人搜救艇而言，迎浪航行時將處于非常平穩的隨波運動狀態，雖然運動幅值大，但是運動周期長而且遠離縱搖垂蕩固有周期，因此運動比較平緩安全，頻域運動預報結果比較合力可靠。反而是Case-T1波長為6.25 m、Case-T2波長為16.9 m，接近或與船體尺度一致；頻率也都是等于或接近縱搖垂蕩固有頻率的狀態，因此存在顯著的波浪船體相互作用，故最終確定這Case-T1&Case-T2為時域模擬工況。無人搜救艇時域計算工況參數見表4。

表4 無人搜救艇時域計算工況參數

5 波浪中運動響應分析

基于剛性船體假定，應用頻域勢流理論的切片法確定船體水動力系數和波浪載荷，建立波浪中船體6自由度運動方程。頻域勢流分析基于切片法理論，切片法的基本思想是在船長方向劃分出一系列橫向切片，忽略切片之間的縱向相互干擾，即將三維船體的水動力振蕩問題簡化為橫向平面的二維流場水動力問題，最后沿船長方向積分即可獲得全船的水動力系數波浪載荷。但該艇需在高海況下的海洋波浪環境下作業，會存在波面破碎、翻卷等強非線性特征，船體在此種環境航行時，又會引發瞬態抨擊、甲板上浪、首尾出入水等強非線性的波浪和船體相互作用問題，對此傳統的勢流方法無能為力。光滑粒子水動力學（Smooth Particle Hydrodynamics，SPH）方法在數值模擬強非線性水動力學問題的顯著優勢，本船體用該法開展數值水池造波、波浪和船體相互作用直接數值模擬[4]。

5.1 波浪中運動的頻域勢流計算分析

該艇體沿船長方向在水線下劃分出40個橫向切片。計算條件設置時，考慮無人搜救艇航速為4 kn；浪向角為從90°、120°、150°到180°；6級海況的波譜選為JONSWAP波浪譜，對應有義波高為6.0 m、譜峰周期為9.993 s；艇體橫搖慣性半徑為船寬的40%，縱搖和首搖慣性半徑為船長的25%，見表5。

表5 各頻域計算工況的結果統計表

由表5可知，橫浪時橫搖角有義值最大，為40.57°；迎浪時縱搖有義值最大，為7.61°；各種浪向下垂蕩有義值基本一致；90°橫浪向艇體運動幅值最大，是對安全性能最不利的情況，而180°迎浪艇體運動幅值最小，是對安全性能最有利的情況。

5.2 波浪中運動的時域計算分析

該艇體航速為4 kn，浪向角為180°迎浪，采用基于SPH方法的數值水池技術，水池左側為推板造波機，可根據需求生成對應波頻、波高的波浪；兩個計算工況波浪參數分別為：Case-T1工況遭遇波周期1.2 s、波高0.62 m，Case-T2工況遭遇波周期2.41 s、波高1.69 m。應用SPH方法模擬波面、艇體時域運動響應，計算分析2個工況艇體運動響應。艇體時域運動響應，計算結果見表6。圖4為Case-T1波浪和艇體典型時刻形態，圖5為Case-T2波浪和艇體典型時刻形態圖[5]。

圖4 Case-T1 波浪和艇體典型時刻形態

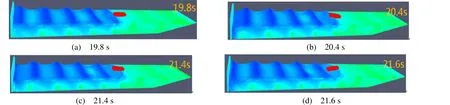
圖5 Case-T2 波浪和艇體典型時刻形態

表6 波浪中無人搜救艇時域運動響應計算結果

由圖4、圖5以及表6結果可知，各計算工況的波陡取為1/10，遠超自然波浪的波陡范圍，波面很快發生翻卷和破碎，波高衰減較快，因此艇體附近的實際波高已經明顯小于理論波高，導致船體實際運動幅值較理論波高下的運動幅值明顯減小。對比2種遭遇波頻的計算結果，可知Case-T2頻率較低時波長較長，波形較穩定，艇體產生了明顯較大的縱搖和垂蕩運動幅值。在6級海況下艇體處于不利波頻時，保證艇體處于迎浪狀態時，航行較為安全。

5 結論

本文通過靜水和波浪中無人搜救艇的穩性評估，6級高海況條件下無人艇的耐波性頻域和時域分析，在選擇有利的180°迎浪向條件下，無人搜救艇可以安全航行。本文無人艇已投入使用，反饋良好，安全性也得到了驗證，此艇的安全分析方法可供類似船體安全評估提供參考。