基于占空比的模型預測電流控制

朱慶祥，張明悅，朱群偉，楊恒瑞

（1. 海軍裝備部廣州局，廣州 510000；2. 92601 部隊，廣東湛江 524009；3. 上海船舶設備研究所，上海 200031）

0 引言

在人類發展歷史中，能源是推動社會進步必不可少的物質，而人類無法大規模地直接利用一次能源，需要將其轉換為電能。在電能的生產和利用過程中，電機都扮演了重要的角色，是實現機械能與電能轉換的關鍵裝置[1]。永磁同步電機省去了轉子繞組和勵磁電源，具有結構簡單、效率高和穩定性強等優點。如何制造出高性能的永磁同步電機和滿足惡劣環境調速要求的控制系統是目前國內外學者極為關注的課題。

20世紀60年代末，矢量控制被首次提出，德國學者首次將其應用在交流調速系統中，矢量控制成為了高性能調速系統的典范[2]。矢量控制利用坐標變換使三相定子電流被分解為2個互相垂直且旋轉的直流分量，并對兩者單獨控制，進而實現對電機輸出的轉矩的控制。傳統的矢量控制均采用PI控制器，而在電機實際的運行過程中，電機是個非線性耦合的模型，電機參數的實時變化會導致PI控制器的性能下降，進而會影響電機的運行狀態[3]。

除傳統的PI控制之外，模型預測控制（Model Predictive Control，MPC）是目前研究的重點，該方法通過設置電機的預測模型，采集電機的各項參數，計算得到最優電壓矢量進而控制電流的輸出。該方法采用離散的數學模型，對計算得出的不同電壓矢量進行在線選擇，選擇最優的電壓矢量輸出并作用于逆變器，省去了PI參數計算調節的過程，結構更加簡單。模型預測控制結構主要包括：預測模型、價值函數、滾動優化。由于每個控制周期都會輸出不同的電壓矢量，逆變器控制開關會頻繁的動作，就會造成電流脈動，轉矩毛刺現象。文獻[4]提出將開關切換次數的多少計入到價值函數中，在選擇最優電壓矢量時考慮開關的切換，以此來降低開關頻率；文獻[5]在尋找最優電壓矢量的過程中，加入快速選擇環節，先得到最優電壓矢量所在扇區，再根據扇區內的有效電壓矢量合成所需的理想電壓矢量。

傳統的模型預測控制算法一個計算周期只輸出一個電壓矢量，無法實現在多個周期內實現電流的無差拍。本文提出一種基于占空比的模型預測控制算法，在一個周期內既輸出有效電壓矢量也輸出零矢量，保證了電壓矢量的選擇為最優。試驗結果證明了在減少電流紋波和轉矩脈動方面的有效性。永磁同步電機MPC控制框圖見圖1。

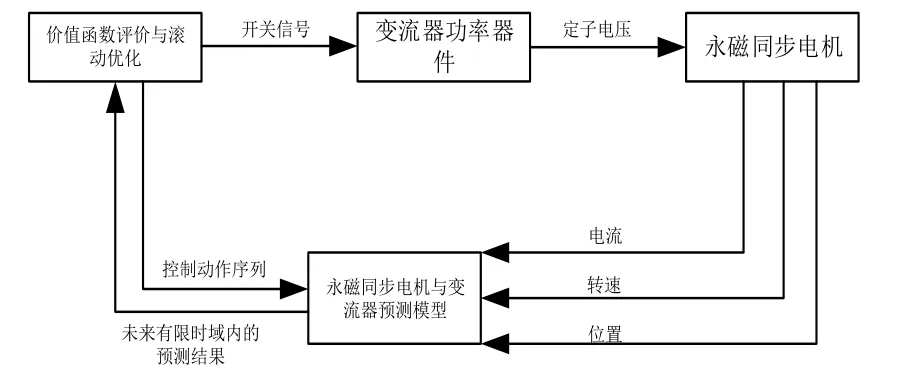
圖1 永磁同步電機MPC 控制框圖

1 永磁同步電機的基本模型

內置式永磁同步電機在d-q軸下的電流方程為

采用前向歐拉法對進行離散化并化簡得到：

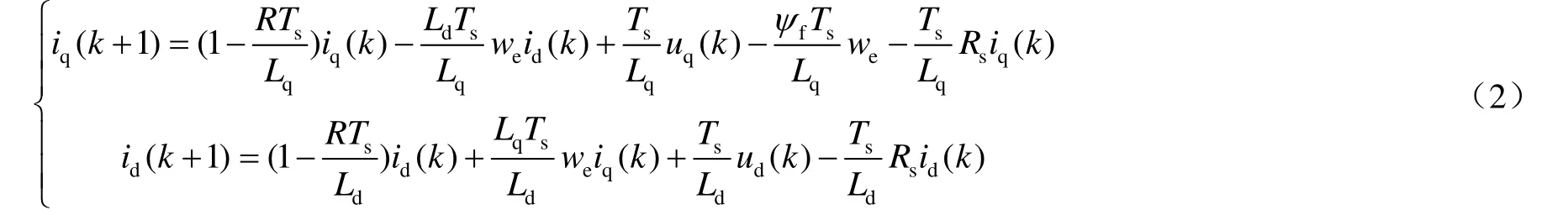
式（1）～式（2）中：Ts為采樣周期；id(k)為k時刻的定子電流直軸分量；iq(k)為k時刻的定子電流交軸分量；id(k+1)為k+1時刻的定子電流直軸分量；iq(k+1) 為k+1時刻的定子電流交軸分量；ud(k) 為k時刻的定子電壓直軸分量；uq(k)為k時刻的定子電壓交軸分量。

價值函數是對預測模型產生的有限個電壓矢量，篩選出最優的電壓矢量作用于逆變器。價值函數的設計主要考慮以下3個方面。

1）電流給定值與采樣值的誤差最小。

2）無功功率最小，轉矩電流比最優。

3）限制定子電流的幅值。

由于本文采用id=0 的控制策略，所以對電流環設計的價值函數為

永磁同步電機模型預測控制的基本框圖見圖2。參考轉速與實際轉速的差值作為轉速控制器的輸入，轉速控制器的輸出作為電流的參考值。通過將當前時刻的電流值作為已知參數輸入到電流預測模型并計算得到下一時刻的電流預測值，與實際參考值作比較，選擇最優的電流值所對應的電壓矢量輸出并作用與逆變器，從而控制電機的運動。

圖2 模型預測控制框圖

2 占空比模型預測控制

在占空比模型預測中，先通過傳統的單矢量模型預測控制選出最優的電壓矢量，其次計算出該電壓矢量所對應的占空比，使得最優電壓矢量只作用占空比的時間，其余時間由零矢量作用，可以保證實際電流與給定電流的誤差最小。這樣便可實現在多個周期內實現電流的無差拍。2種模型預測控制電壓矢量對比見圖3。

圖3 2 種模型預測控制電壓矢量對比

1）占空比的計算

本文以q軸為例，通過分配電壓矢量和零矢量來使得iq在一個采樣周期內到達給定電流。即

式中：sopt為電壓矢量的斜率；s0為零矢量的斜率；topt為最優電壓矢量的作用時間。

其中，sopt、s0的計算公式為

式中：γ為電壓矢量所對應的占空比，將占空比的大小限制在[0, 1]。

3 試驗分析

3.1 仿真分析

本次試驗的電機數據見表1，仿真時長設為0.7 s，電機轉速設置為1 000 r/min。

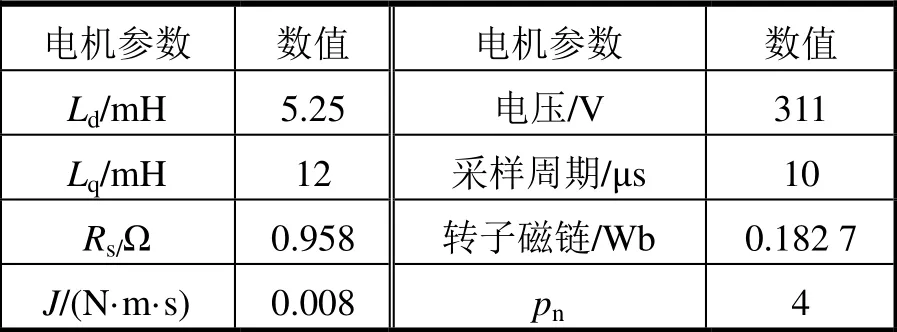
表1 Simulink 仿真參數表

3.2 負載突變

在負載變化試驗中，初始時刻電機負載轉矩為0，在0.3 s時，增加大小為的20 N·m負載轉矩，在0.5 s時，將負載轉矩降為10 N·m。其仿真波形見圖4。

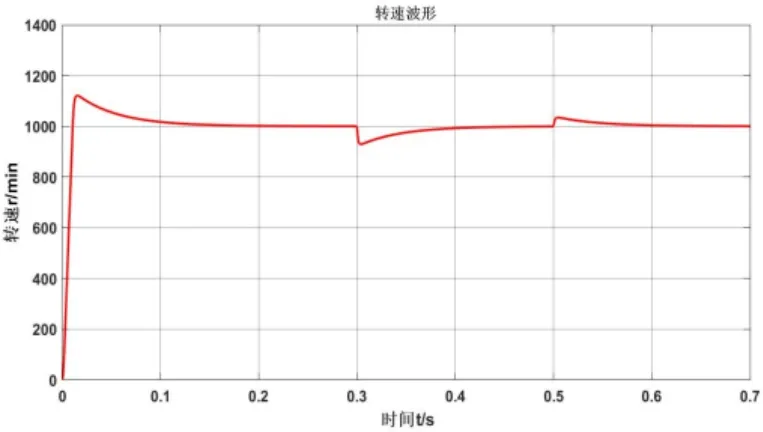
圖4 轉速波形變化

當電機啟動時，電機轉速迅速上升，在0.02 s時達到最大值，轉速的超調量為11.3%，在0.12 s時，轉速穩定在給定轉速；在0.3 s時，電機負載突增至20 N·m，轉速收到擾動，轉速先降后升，在0.1 s之內恢復，并穩定在給定轉速；在0.5 s時，電機負載突降，轉速先升后降，轉速在0.07 s之內穩定在給定轉速。在模型預測控制下的永磁同步電機，面對負載突變時，可以很快穩定轉速，動態性能良好。

在電機啟動時。兩者控制方式下的轉矩迅速上升，當電機轉速穩定后，轉矩下降到接近，此時電機處于空載運行狀態。在0.3 s時，電磁轉矩迅速上升至20 N·m，此時電機處于帶載運0行狀態；在0.5 s時，負載突降至10 N·m，電磁轉矩迅速下降。在運行過程中，兩者均滿足電機的電磁轉矩方程。從圖5(a)和圖5(b)的對比中可以看出，當電機運行時，傳統模型預測空載的轉矩脈動明顯大于占空比模型預測空載的轉矩脈動。

圖5 轉矩波形變化

從圖6(a)和圖6(b)的對比中可以看出在電機啟動時，兩者控制方式下的電流的變化曲線無很大變化，幅值均接近30 A。當電機處于空載運行時，占空比模型預測控制下的電機定子電流的諧波成分更少，電流的正弦性更好。在0.3 s時，負載增加，三相定子電流在極短的時間內穩定，幅值約為20 A，兩者的正弦性良好。

圖6 三相定子電流波形變化

從圖7對比分析，兩者的q軸電流響應變化曲線沒有太大變化。電機啟動時，q軸電流的數值一樣；0.3 s時，上升速度、上升峰值，均無明顯變化。在占空比模型預測控制中，電流的脈動更小，紋波更小，驗證了文獻[6]的結論。

圖7 q 軸電流響應

從圖8(a)和圖8 (c)對比來看，在改進后的模型預測控制下，永磁同步電機在空載運行時三相定子電流12.39%的諧波率遠小于傳統控制下23.89%的電流諧波率。當帶載運行時，兩者的三相電流諧波率接近。

圖8 頻譜分析

4 結論

由于傳統的模型預測控制一個控制周期只輸出一個有效的電壓矢量，所以會造成電機穩態性能差，電流跟隨效果不佳的狀況。本文針對傳統模型預測控制存在的問題，提出讓有效電壓矢量與零矢量相結合，兩者共同作用同一個控制周期，并分別計算出兩者的作用時間，可以使預測電流與電流給定值誤差更小。本文通過Simulink軟件仿真驗證了該方法保證了抗干擾能力的同時，有效地降低了轉矩的脈動、毛刺現象和空載時刻三相電流的諧波率，電流控制效果更加優異，q軸電流的跟隨效果更好，波動量更小。