一類隨機對流擴散方程的反源問題*

趙麗志， 馮曉莉

（西安電子科技大學 數(shù)學與統(tǒng)計學院，西安 710126）

引 言

隨著科學技術的快速發(fā)展，反問題在環(huán)境科學、能源開發(fā)、流體力學、醫(yī)學、金融等領域有了越來越廣泛的應用.所謂反問題就是指用解的一些已知數(shù)據(jù)去重構問題中的未知數(shù)據(jù)[1-3].由于隨機偏微分方程在腦磁成像[4]、光聲成像[5]、超聲成像[6]、天線設計與合成[7-8]等方面有著重要的應用，所以受到了廣大學者的關注.特別地，隨機反源問題作為隨機反問題中的一類，目前已有很多學者做了相關研究，比如文獻[9] 通過Carleman 估計證明了隨機源項的唯一性；文獻[10]研究了一維隨機熱方程模擬的無限桿中的反源問題，并通過求解Fredholm 積分方程重構了隨機源項的均值和方差.

近年來，帶有Hurst 參數(shù)(H∈(0,1))的分數(shù)階Brown 運動在科學和工程領域中有著廣泛的應用，目前關于帶有不同類型隨機源項的時間分數(shù)階擴散方程的反源問題已有一些成果.對于H=1/2的情形，文獻[11]討論了帶有離散隨機噪聲的時間分數(shù)階擴散方程的反源問題；文獻[12] 運用終止時刻的數(shù)據(jù)u(x,T,ω)的統(tǒng)計信息確定了時間分數(shù)階擴散方程的源項f(x)h(t)+g(x)ω˙(t)中 的f(x)和 |g(x)|，更多相關研究可參考文獻[13-17]. 對于H∈(0,1)的 情形，文獻[18]研究了帶有f(x)h(t)+g(x)B˙H(t)隨機源項的時間分數(shù)階擴散方程，并根據(jù)終止時刻的數(shù)據(jù)u(x,T,ω)重 構了f(x)和 |g(x)|；類似地，文獻[19]考慮了另一個時間分數(shù)階擴散方程；文獻[20]為分數(shù)階Gauss 噪聲驅動下的隨機非線性分數(shù)階擴散方程的數(shù)值分析提供了一個統(tǒng)一的框架.目前，由于對帶有分數(shù)階Brown 運動的隨機偏微分方程的討論還處于研究初期，并且關于對流擴散方程還沒有相關的研究，因此，本文將討論如下由分數(shù)階Brown 運動驅動的隨機對流擴散方程：

1 預 備 知 識

2 正 問 題

本節(jié)將在以下假設成立的條件下討論問題(1)的適定性.

假設1 設H∈(0,1)并 且f， σ，g∈L?2(D). 假設h∈L∞(0,T)是一個非負函數(shù)并且有一個正的下界，即h≥Ch>0.

由式 (7)得

所以

證明 根據(jù)式(12)、(20)和(22)易得結論.

3 源項反演問題

本節(jié)將通過終止時刻的數(shù)據(jù)u(x,T,ω)的 一些統(tǒng)計量來重構源項中的f(x)和 σ2(x)，并且分別討論它們的唯一性與不穩(wěn)定性，其中

3.1 f(x)和 σ 2(x)的唯一性

由式(7)可得

3.2 反演 f(x)和 σ 2(x)的不穩(wěn)定性

3.2.1 反演f(x)的不穩(wěn)定性

由積分中值定理，可知

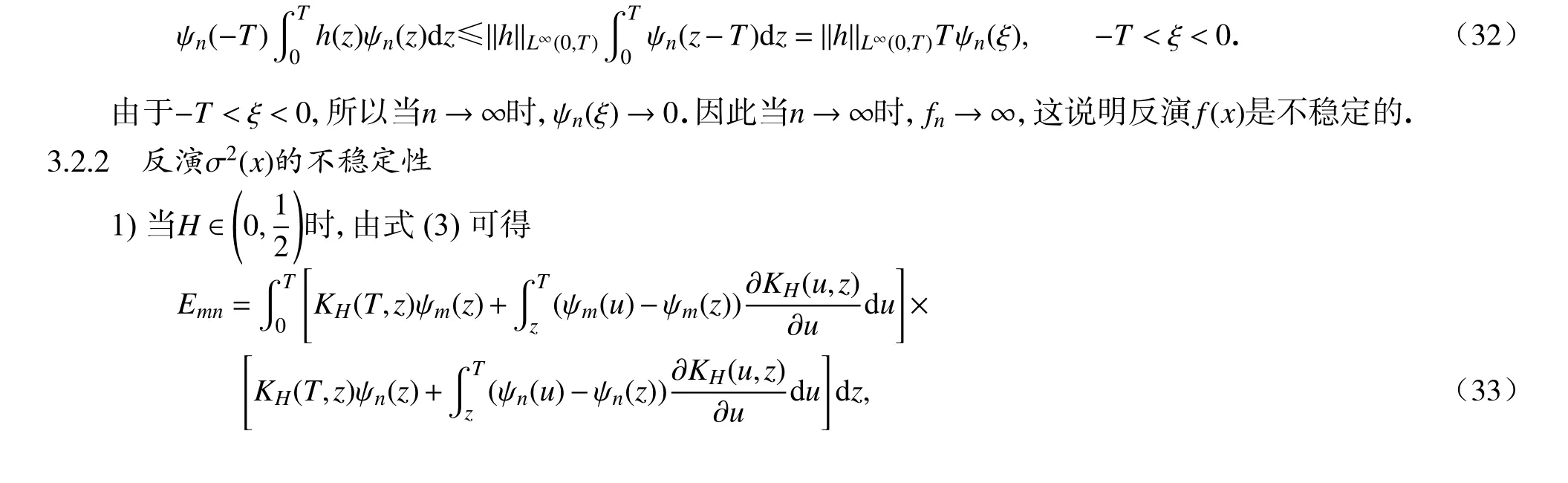
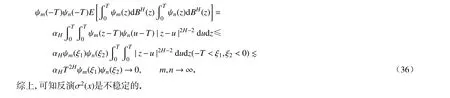
4 數(shù) 值 實 驗

圖1 H =0.9,δ=0.04 時 f 和σ 2的相對誤差Fig. 1 The relative errors of the reconstruction for f and σ 2 with respect to H =0.9 andδ=0.04

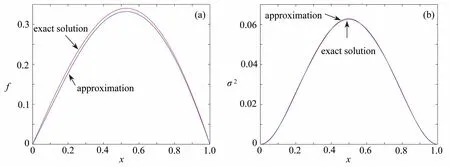
圖2 H =0.4,N=6 時的 f 和σ2Fig. 2 The reconstruction of f and σ 2 for the inverse problem with H =0.4 andN=6

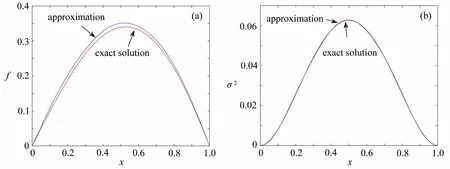
圖3 H =0.5,N=6 時的 f 和σ2Fig. 3 The reconstruction of f and σ 2 for the inverse problem with H =0.5 andN=6

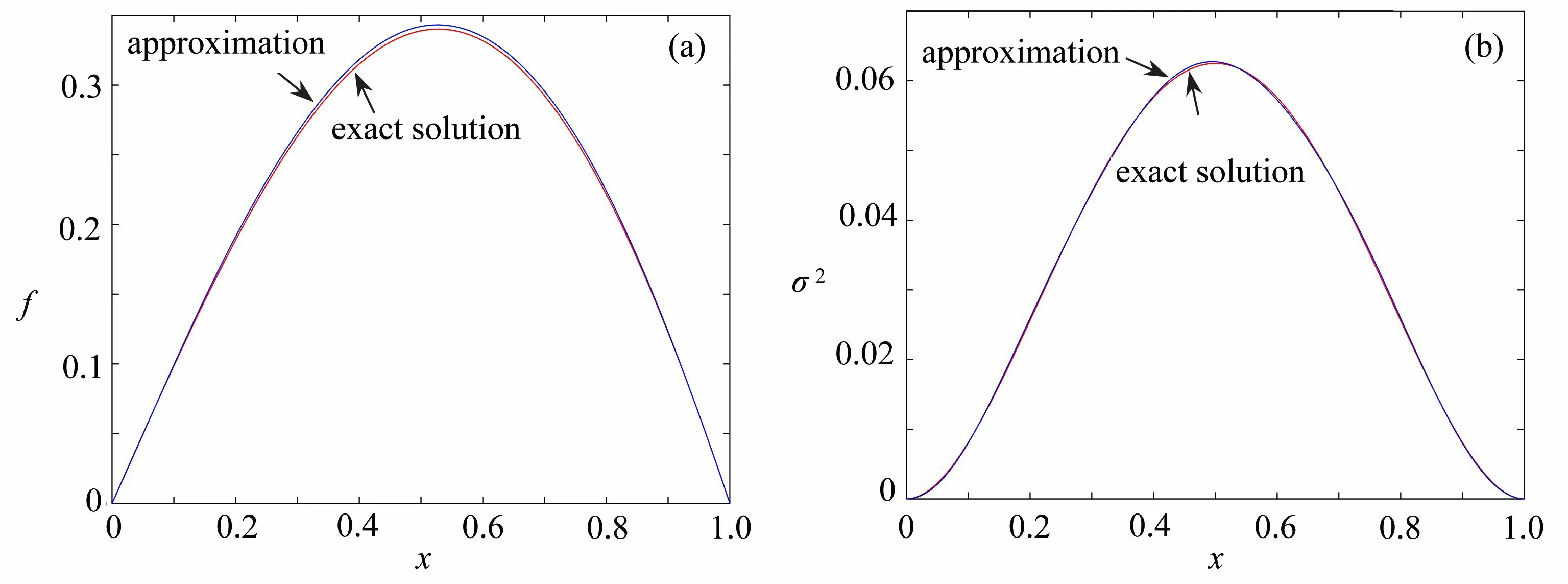
圖4 H =0.9,N=6 時的 f 和σ2Fig. 4 The reconstruction of f and σ 2 for the inverse problem with H =0.9 andN=6

5 結 論

在本文中，我們討論了帶有分數(shù)階Brown 運動隨機源項的一維隨機對流擴散方程.在正問題部分通過對溫和解的期望的討論，證明了其適定性.在反隨機源部分，給定T時刻的數(shù)據(jù)來反演源項，證明了反演的唯一性與不穩(wěn)定性.最后通過有限差分法和截斷正則化方法進行數(shù)值模擬證明了理論部分的合理性，并且得出了Hurst 參數(shù)H越大，反演效果越好的結論.雖然本文只討論了一維隨機對流擴散方程，但是關于高維的情形也可以類似討論.

參考文獻（ References ） ：

［1］ 李曉曉, 郭亨貞, 萬詩敏, 等. 一類對流-擴散方程熱源識別反問題[J]. 蘭州理工大學學報, 2012, 38（3）: 147-149. （LI Xiaoxiao, GUO Hengzhen, WAN Shimin, et al. A class of inverse problem of identification of heat source term in convection-diffusion equation[J].Journal of Lanzhou University of Technology, 2012, 38（3） : 147-149.（ in Chinese））

［2］ 賈現(xiàn)正, 張大利, 李功勝, 等. 空間-時間分數(shù)階變系數(shù)對流擴散方程微分階數(shù)的數(shù)值反演[J]. 計算數(shù)學, 2014, 36（2）:113-132. （JIA Xianzheng, ZHANG Dali, LI Gongsheng, et al. Numerical inversion of the fractional orders in the space-time fractional advection-diffusion equation with variable coefficients[J].Mathematica Numerica Sinica,2014, 36（2）: 113-132.（in Chinese））

［3］FURATI K M, IYIOLA O S, KIRANE M. An inverse problem for a generalized fractional diffusion[J].Applied Mathmatics and Computation, 2014, 249: 24-31.

［4］AMMARI H, BAO G, FLEMING J L. An inverse source problem for Maxwell’s equations in magnetoencephalography[J].SIAM Journal on Applied Mathematics, 2002, 62（4）: 1369-1382.

［5］ANASTASIO M A, ZHANG J, MODGIL D, et al. Application of inverse source concepts to photoacoustic tomography[J].Inverse Problems, 2007, 23（6）: S21-S35.

［6］DEVANEY A J. Inverse source and scattering problems in ultrasonics[J].IEEE Transaction on Sonics and Ultrasonics, 1983, 30（6）: 355-363.

［7］MARENGO E A, DEVANEY A J. The inverse source problem of electromagnetics: linear inversion formulation and minimum energy solution[J].IEEE Transaction on Antennas and Propagation, 1999, 47（2）: 410-412.

［8］MARENGO E A, KHODJA M R, BOUCHERIF A. Inverse source problem in nonhomogeneous background media, Ⅱ: vector formulation and antenna substrate performance characterization[J].SIAM Journal on Applied Mathematics, 2008, 69（1）: 81-110.

［9］Lü Q. Carleman estimate for stochastic parabolic equations and inverse stochastic parabolic problems[J].Inverse Problems, 2012, 28（4）: 045008.

［10］CHEN S L, WANG Z W, CHEN G L. Cauchy problem of non-homogenous stochastic heat equation and application to inverse random source problem[J].Inverse Problems and Imaging, 2021, 15（4）: 619-639.

［11］TUAN N H, NANE E. Inverse source problem for time-fractional diffusion with discrete random noise[J].Statistics and Probability Letters, 2017, 120: 126-134.

［12］NIU P P, HELIN T, ZHANG Z D. An inverse random source problem in a stochastic fractional diffusion equation[J].Inverse Problems, 2020, 36（4）: 045002.

［13］LIU C. Reconstruction of the time-dependent source term in stochastic fractional diffusion equation[J].Inverse Problems and Imaging, 2020, 14（6）: 1001-1024.

［14］FU S B, ZHANG Z D. Application of the generalized multiscale finite element method in an inverse random source problem[J].Journal of Computational Physics, 2021, 429: 110032.

［15］GONG Y X, LI P J, WANG X, et al. Numerical solution of an inverse random source problem for the time fractional diffusion equation via PhaseLift[J].Inverse Problems, 2021, 37: 045001.

［16］LI P J, WANG X. An inverse random source problem for Maxwell’s equations[J].SIAM Journal on Multiscale Modeling and Simulation, 2021, 19（1）: 25-45.

［17］LI P J, WANG X. An inverse random source problem for the one-dimensional Helmholtz equation with attenuation[J].Inverse Problems, 2021, 37（1）: 015009.

［18］FENG X L, LI P J, WANG X. An inverse random source problem for the time fractional diffusion equation driven by a fractional Brownian motion[J].Inverse Problems, 2020, 36（4）: 045008.

［19］NIE D X, DENG W H. An inverse random source problem for the time-space fractional diffusion equation driven by fractional Brownian motion[EB/OL]. (2021-06-02)[2022-02-12]. https://arxiv.org/abs/2106.00917.

［20］NIE D X, DENG W H. A unified convergence analysis for the fractional diffusion equation driven by fractional Gaussion noise with Hurst indexH∈(0, 1)[J].SIAM Journal on Numerical Analysis, 2022, 60（3）: 1548-1573.