可交換的Toeplitz算子①

丁宣浩，梁煥超，李永寧

1.重慶工商大學 數學與統計學院，重慶 400067；2.經濟社會應用統計重慶市重點實驗室，重慶 400067

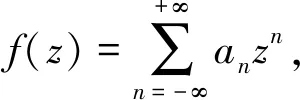
(1)

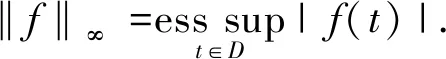
在函數空間上的算子理論中，我們主要關注的是不同函數空間上的Toeplitz算子的交換性問題，例如Hardy空間、Bergman空間、Dirichlet空間、Fock空間等． 文獻[7]給出了經典Hardy空間上兩個Toeplitz算子可交換的充分必要條件，樹立了Toeplitz算子理論研究的典范．

引理1[7]設f，g∈L∞，則TfTg=TgTf當且僅當下列條件之一成立：

(i)f，g均是解析的，即f∈H∞且g∈H∞；

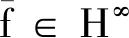
(iii)f，g的非平凡線性組合是常數，即存在a，b，c∈C且|a|+|b|>0，使得af+bg=c．

文獻[8]給出了TfTg-TgTf是緊算子的充分必要條件． 文獻[2]完全刻畫了TfTg-TgTf是有限秩的情況． 文獻[3]應用Berezin變換和調和延拓的方法進行研究，給出了雙圓盤Hardy空間上的兩個Toeplitz算子可交換的充分必要條件． 由兩個Toeplitz算子的乘積到n個Toeplitz算子的乘積，曾經有一個歷時很久的公開問題，即當n個Toeplitz算子的乘積為0時，是否必有一個Toeplitz算子為0?該問題稱為Toeplitz算子的零積問題． 文獻[7]證明了：兩個Toeplitz算子的乘積為0，其中必有一個為0． 文獻[9]用巧妙的方法證明了：5個Toeplitz算子的乘積為0，其中必有一個為0． 文獻[10]證明了6個Toeplitz算子的乘積的情況也成立． 最終，文獻[11]對n個Toeplitz算子的零積問題給出了肯定的回答． 受Toeplitz算子的零積問題的啟發，很自然地，我們想知道n個Toeplitz算子的乘積在什么條件下是可交換的． 本文借助Brown-Halmos定理，應用Coburn引理[4]，得到了n個Toeplitz算子可交換的充要條件．

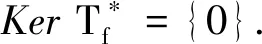
命題1若f∈L∞，f|E=0，f|?D-E≠0，E??D，E的測度大于0且小于1，則KerTf={0}．

證設x∈H2使得Tfx=0，則有

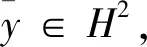
依據KerA=(RanA*)⊥對任意有界線性算子A成立，再由命題1，我們有下面的Coburn引理的變形：

引理3(Coburn引理的變形)設f∈L∞且f為非零函數，則KerTf={0}或cl(RanTf)=H2，這里cl(RanTf)表示Tf的值域的閉包．

1 可交換性

在本節當中，通過應用Brown-Halmos定理[7]和數學歸納法得到了Hardy空間上任意有限多個Toeplitz算子任意次序可交換的充要條件．

定理1設fi∈L∞為非零函數(i=1，2，…，n)，則對所有的置換σ∈Sn，Tfσ(1)Tfσ(2)…Tfσ(n)=Tf1Tf2…Tfn當且僅當下列條件之一成立：

(i)當i=1，2，…，n時，每個fi都是解析的；

(ii)當i=1，2，…，n時，每個fi都是余解析的；

(iii)對任意的1≤i，j≤n，且i≠j時，fi與fj的非平凡線性組合是常數．

證利用引理1，充分性顯然成立，因此只需證明結論的必要性，我們將通過數學歸納法證明．

當n=2時，由引理1的結果可知結論成立，下面進入歸納步驟． 假設當n=k>2時結論成立，即由

Tfσ(1)…Tfσ(2)Tfσ(k)=Tf1Tf2…Tfk

必有條件(i)—(iii)之一對fi(i=1，2，…，k)成立，其中σ是集合{1，2，…，k}到其自身上的一個置換．

需證任意k+1個Toeplitz算子可交換，則條件(i)—(iii)之一成立． 設k+1個Toeplitz算子可交換．

若f1，f2，…，fk，fk+1當中有一個為常數，則k+1個Toeplitz算子相乘就轉變成了至多k個Toeplitz算子相乘，由歸納假設，結論成立．

若f1，f2，…，fk，fk+1都不為常數，由k+1個Toeplitz算子可交換，則有

Tfσ(1)…Tfσ(k)Tfk+1=Tf1…TfkTfk+1

(2)

以及

Tfk+1Tfσ(1)…Tfσ(k)=Tfk+1Tf1…Tfk

(3)

根據引理3可知：若KerTfk+1={0}，由等式(2)推出

Tfσ(1)Tfσ(2)…Tfσ(k)=Tf1Tf2…Tfk

若cl(RanTfk+1)=H2，則由等式(3)仍可推出

Tfσ(1)…Tfσ(k)=Tf1…Tfk

由歸納假設，f1，f2，…，fk滿足條件(i)—(iii)之一．

同樣由Tf1，…Tfk，Tfk+1可交換，則有

Tf1Tfσ′(2)…Tfσ′(k+1)=Tf1Tf2…Tfk+1

以及

Tfσ′(1)…Tfσ′(k)Tfk+1=Tf1…TfkTfk+1

其中σ′是集合{2，3，…，k+1}到其自身上的一個置換． 類似地，可得

Tfσ′(2)…Tfσ′(k+1)=Tf2…Tfk+1

由歸納假設，f2，f3，…，fk+1滿足條件(i)—(iii)之一．

下面分3種情形討論：

情形1 由f1，f2，…，fk都解析，可推出fk+1也解析．

若f2，…，fk，fk+1解析，當然fk+1也解析．

若f2，…，fk，fk+1共軛解析，則f2，f3，…，fk既解析又共軛解析，那么f2，f3，…，fk都為常數，與前提不符．

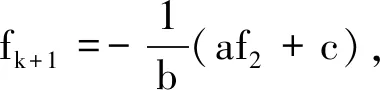
情形2 由f1，f2，…，fk都共軛解析，類似于情形1的討論可推出fk+1也共軛解析．

情形3 由f1，f2，…，fk兩兩非平凡線性組合為常數，可推出f1，f2，…，fk，fk+1滿足條件(i)—(iii)之一．

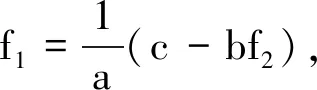
若f2，…，fk，fk+1共軛解析，類似地可得f1也共軛解析．

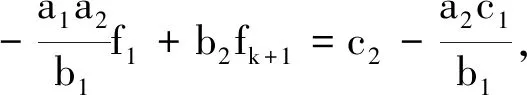
由此可得，對所有的fi(i=1，2，…，k，k+1)，這k+1個函數一定滿足條件(i)—(iii)之一．

綜上所述，通過數學歸納法，對任意正整數n，定理1成立．

2 模去有限秩算子后的交換性

文獻[2]刻畫了兩個Toeplitz算子模去有限秩算子可交換的條件． 下面，通過進一步研究得到了任意有限個Toeplitz算子模去有限秩算子可交換的刻畫，結論如下：

定理2設fi∈L∞為非零函數(i=1，2，…，n)，則對所有的置換σ，有

Tfσ(1)Tfσ(2)…Tfσ(n)=Tf1Tf2…Tfnmod(F)

成立當且僅當對任意的1≤i，j≤n且i≠j，TfiTfj=TfjTfimod(F)，其中F為有限秩算子全體．

證充分性顯然，因此只需要證明結論的必要性． 下證必要性． 當n=3時，對所有置換σ，有

Tfσ(1)Tfσ(2)Tfσ(3)=Tf1Tf2Tf3mod(F)

則

Tf1Tfσ′(2)Tfσ′(3)=Tf1Tf2Tf3mod(F)

從而有

Tf1(Tf3Tf2-Tf2Tf3)=F1

其中F1為有限秩算子． 又由引理3知有以下兩種情況發生：

情形1 若KerTf1={0}，則Tf1為單射． 由

Tf1(Tf3Tf2-Tf2Tf3)H2=F1H2

得(Tf3Tf2-Tf2Tf3)H2為有限維的． 從而

Tf2Tf3=Tf3Tf2mod(F)

情形2 若cl(Tf1H2)=H2，根據

(Tf2Tf3-Tf2Tf3)Tf1=F2

其中F2為有限秩算子，則有

cl[(Tf3Tf2-Tf2Tf3)Tf1H2]=cl(F2H2)

(Tf3Tf2-Tf2Tf3)Tf1xn∈M

由于M為閉的，故有

(Tf3Tf2-Tf2Tf3)x∈M

因此可得

(Tf3Tf2-Tf2Tf3)H2?M

故Tf2Tf3-Tf3Tf2=0 mod(F)，即Tf2Tf3=Tf3Tf2mod(F)．

同理，根據

Ff2(Tf3Tf1-Tf1Tf3)=0 mod(F)

以及

Tf3(Tf1Tf2-Tf2Tf1)=0 mod(F)

分別可推出

Tf1Tf3=Tf3Tf1mod(F)

Tf2Tf1=Tf1Tf2mod(F)

因此，結論成立．

假設當n=k>3時結論成立，即如果

Tfσ″(1)Tfσ″(2)…Tfσ″(k)=Tf1Tf2…Tfkmod(F)

其中σ″是集合{1，2，…，k}到其自身上的一個置換，則有

TfiTfj=TfjTfimod(F)1≤i，j≤n；i≠j

當n=k+1時，由于Tfσ(1)Tfσ(2)…Tfk+1=Tf1Tf2…Tfk+1mod(F)，則有

Tf1Tfσ″(2)…Tfσ″(k+1)=Tf1Tf2…Tfk+1mod(F)

從而有

Tf1(Tfσ?(2)…Tfσ?(k+1)-Tf2…Tfk+1)=F3

其中，F3為有限秩算子，這里σ?為{2，3，…，k+1}到其自身上的一個置換．

再次應用引理3，同理可得Tfσ?(2)…Tfσ?(k+1)-Tf2…Tfk+1為有限秩算子． 又由n=k時結論成立知

TfiTfj=TfjTfimod(F)

這里2≤i，j≤k+1，且i≠j．

類似n=3的情況，同理可證：對任意的1≤i，j≤k+1且i≠j，TfiTfj=TfjTfimod(F)成立．

綜上所述，對所有的自然數n，定理2成立．

3 結束語

針對Hardy空間上Toeplitz算子的交換性問題，通過借助Brown-Halmos定理，應用Coburn引理和數學歸納法得到了n個Toeplitz算子可交換的充要條件，并對任意有限個Toeplitz算子模去有限秩算子可交換的充分必要條件進行了刻畫． 文獻[8]給出了TfTg-TgTf是緊算子的充分必要條件． 對于何種條件下，任意有限多個有界Toeplitz算子的乘積模去緊算子可交換的問題，也是一個有趣的問題，有待進一步的研究．

問題設fi∈L∞為非零函數(i=1，2，…，n)，則對所有的置換σ，

Tfσ(1)Tfσ(2)…Tfσ(n)=Tf1Tf2…Tfnmod(K)

成立的充分必要條件是什么？其中K為緊算子全體．