四元數矩陣的直積分解及最佳逼近①

黃敬頻，白瑞，徐云，趙耿威

廣西民族大學 數學與物理學院，南寧 530006

四元數在圖像處理及數學基礎理論的研究方面均有重要作用[1-2]． 作為矩陣關聯運算的普通乘積和直積(也稱Kronecker積或張量積)，具有廣泛的應用性和普適性[3-5]． 文獻[6]利用直積理論提出了群對稱原子或分子軌道中產生對稱軌道的標準方法與封閉公式． 文獻[7]根據Toeplitz矩陣可分解為Kronecker積的和的性質，提出了一種基于卷積核矩陣的圖像迭代復原方法． 文獻[8]以直積為主要工具研究了四元數矩陣方程AXB+CXD=E的M自共軛解． 文獻[9-10]討論了有關Kronecker積的最小二乘問題及其在二元多項式回歸中的應用． 多年來，關于矩陣Kronecker積性質的研究已有豐富的成果[11-13]． 關于矩陣方根的求解方面，文獻[14-15]分別采用Schur分解和牛頓迭代方法給出了實矩陣的方根計算，文獻[16]運用冪法給出了復矩陣的方根計算，文獻[17]利用拉直算子討論了復矩陣Kronecker方根的存在性，文獻[18]利用牛頓迭代方法給出了Einstein積意義下實張量的方根計算． 目前未見關于四元數矩陣的Kronecker積分解問題的研究報導，針對這一問題，本文著重考慮直積意義下四元數矩陣的分解及最佳逼近問題．

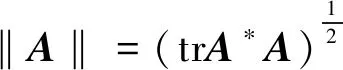
定義1設X=(xij)∈Qm×n，Y=(yij)∈Qs×t，稱

(1)

是X與Y的Kronecker積． 當X，Y中有一個是實矩陣時，稱X?Y為弱直積[2]．

本文具體討論如下2個問題：

問題1給定四元數矩陣A∈Qm2×n2，尋找X，Y∈Qm×n使得A=X?Y． 當此分解式不存在時，求F(X，Y)=‖X?Y-A‖的最佳逼近值．

問題2對問題1給定的四元數矩陣A，求直積意義下滿足X?X=A的二次方根X的存在條件及計算公式．

1 主要結果

引理1設四元數q=a0+a1i+a2j+a3k∈QR，則q的方根總存在，并可表示為

(2)

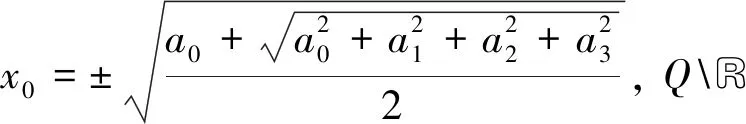
證設x=x0+x1i+x2j+x3k，且q=x2，直接展開比較可得

(3)

(4)

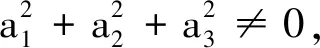
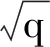
對A∈Qm2×n2作如下分塊

(5)

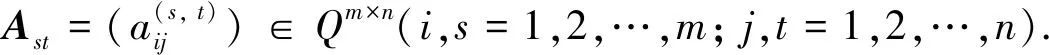
L=(Vec(A11)，…，Vec(A1n)，…，Vec(Am1)，…，Vec(Amn))∈Qmn×mn

(6)

于是關于問題1的解，有如下結果：

定理1設非零矩陣A∈Qm2×n2有分塊式(5)，則存在X，Y∈Qm×n，使得A=X?Y的充要條件是rank(L)=1，其中L如(6)式所示．

證若存在X0=(xij)，Y0∈Qm×n，使得A=X0?Y0，則由Kronecker積的定義及(5)式可得

Aij=xijY0i=1，2，…，m；j=1，2，…，n

當且當

Vec(Aij)=xijVec(Y0)

因此

L=(x11Vec(Y0)，…，x1nVec(Y0)，…，xm1Vec(Y0)，…，xmnVec(Y0))∈Qmn×mn

由于A≠0，因此X0≠0，Y0≠0，從而rank(L)=1． 反之，若rank(L)=1，不妨設Vec(A11)≠0，則L各列有比例關系

Vec(Aij)=kijVec(A11)

因此有

Aij=kijA11i=1，2，…，m；j=1，2，…，n

取X0=(kij)，Y0=A11，則存在分解式A=X0?Y0． 證畢．

注2由定理1的證明過程可知，當A的Kronecker積分解存在時，只要確定Y0以及所有Aij的左比例系數kij，那么X0=(kij)和Y0就是A的一組分解．

同時可得如下推論：

推論1在定理1的條件下，四元數矩陣A存在Kronecker積分解的充要條件是存在四元數向量u，v∈Qmn×1使得L=uvT．

證根據定理1及rank(L)=1可知，存在可逆矩陣P，Q∈Qmn×mn，使得

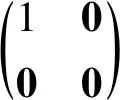
當A的Kronecker積分解不存在時，我們討論它的最佳逼近問題． 對此，假設(6)式中L的奇異值分解為

(7)

其中U，V∈Umn×mn均為四元數酉陣，r=rank(L)，Σr=diag(d1，…，dr)，d1≥…≥dr>0． 根據推論1可知，求F(X，Y)=‖X?Y-A‖的最佳逼近值，等價于求u，v∈Qmn×1使得

‖uvT-L‖=min

(8)

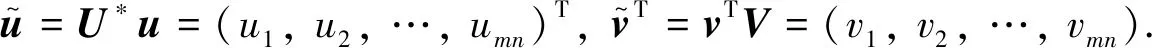
定理2設非零矩陣A∈Qm2×n2有分塊式(5)和(6)，則存在u，v∈Qmn×1使得(8)式成立，其中

(9)

U(·，1)，V*(1，·)分別是(7)式中U，V*的第1列和第1行，d1是L的最大奇異值．

證根據L的奇異值分解(7)式以及Frobenius范數酉乘積不變性得

(10)

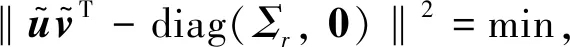
‖(u1，u2，…，umn)T(v1，v2，…，vmn)-diag(d1，…，dr，0，…，0)‖2=min

(11)

根據diag(d1，…，dr，0，…，0)的對稱半正定性，可取

ui=vi∈Ri=1，…，r

ui=vi=0i=r+1，…，mn

因此由(11)式得

(12)

其中δij∈{0，1}． 對(12)式中函數f(u1，…，ur)求偏導數，得

(13)

方程組(13)等價于

由此可得

ui=0

或

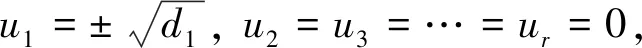
再由U*u=(u1，u2，…，umn)T，vTV=(v1，v2，…，vmn)，可得

即表達式(9)成立． 證畢．

根據四元數方根總存在的特點，可得問題2的解如下：

Ast=bstBs=1，2，…，m；t=1，2，…，n

(14)

這時X0=B∈Qm×n就是A的二次方根．

證充分性是顯然的． 下證必要性． 若存在X0=B=(bij)∈Qm×n使得A=B?B，則由分塊式(5)可得

Ast=bstBs=1，2，…，m；t=1，2，…，n

(15)

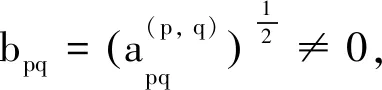
注3當(14)式成立時，顯然有rank(L)=1，因此rank(L)=1是A的二次方根存在的必要條件，但不是充分的(見算例1)．

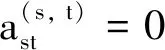
2 數值算例

例1已知四元數矩陣

試討論是否存在X，Y∈Q2×3，使得A具有Kronecker積分解．

解對A作分解式(5)，得

其中

直接計算可知

rank(L)=rank(Vec(A11)，Vec(A12)，Vec(A13)，Vec(A21)，Vec(A22)，Vec(A23))=1

因此，根據定理1可知，存在X0，Y0∈Q2×3，使得A=X0?Y0． 事實上，由

得Kronecker積分解

例2已知四元數矩陣

試討論A的二次方根的存在性．

解對A作分解式(5)，得

其中

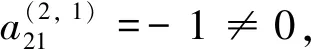
直接計算可知

Ast=bstBs=1，2；t=1，2，3

根據定理3，A存在二次方根X0=B，即

3 結論

對于給定的m2×n2四元數矩陣A，利用A的分塊矩陣(5)式，并由Vec構造的mn×mn矩陣L的秩，獲得A具有直積分解的充要條件及其分解方法． 當此類分解不存在時，由L的奇異值分解，以及求F(X，Y)=‖X?Y-A‖的最佳逼近解等價于求極小范數問題(8)，得到了問題1的解． 對于問題2，應用四元數方根的存在性與Kronecker積的定義，得到了X?X=A成立的充要條件及其直積意義下二次方根X的計算公式．