湍流邊界層激勵下平板振動響應(yīng)相似性研究
趙國亮, 陳美霞
(華中科技大學(xué) 船舶與海洋工程學(xué)院, 武漢 430074)
當(dāng)潛艇在水下航行時,在其外壁會產(chǎn)生湍流邊界層,因邊界層內(nèi)流體質(zhì)點的運動速度是隨機存在的,故在湍流邊界層內(nèi)部會產(chǎn)生非定常的隨機脈動壓力,這種隨機的湍流脈動壓力激勵結(jié)構(gòu)會使外壁產(chǎn)生振動并向外輻射噪聲,也被稱為“流激振動”或“流激響應(yīng)”,它是水下結(jié)構(gòu)水動力噪聲的重要組成部分。
對于水下結(jié)構(gòu)的流激噪聲問題,因湍流脈動壓力是隨機產(chǎn)生的,理論分析比較困難,縮比模型試驗成為研究流激噪聲的重要技術(shù)途徑。因此,必然會遇到模型與原型之間振動響應(yīng)的相似關(guān)系問題。
若將湍流邊界層的脈動壓力作為隨機信號,水下結(jié)構(gòu)流激振動問題便可歸于傳統(tǒng)的隨機聲學(xué)問題。Hwang等[1]對1960年—2004年間的各種湍流邊界層壁面壓力譜模型的發(fā)展進行了綜述,并使用這些模型與各種試驗場景下測得的數(shù)據(jù)進行了對比,初步討論了壁面壓力譜的相似換算,其中Goody[2]提出的壓力譜半經(jīng)驗?zāi)P湍軌蛟谳^寬的頻帶內(nèi)提供較好的頻譜預(yù)測,但未明確歸一化方法在不同介質(zhì)的壁面壓力譜間的適用性。
壁面壓力譜也被應(yīng)用于流激結(jié)構(gòu)振動響應(yīng)領(lǐng)域的研究, Rosa等[3]采用Corcos[4]模型作為輸入,采用模態(tài)疊加法計算了鋁板一側(cè)受湍流壁面脈動壓力激勵的結(jié)構(gòu)振動響應(yīng),與數(shù)值仿真計算結(jié)果吻合較好。 Franco等[5]則對湍流邊界層激勵下平板響應(yīng)的相似性定律進行了研究,對不同尺寸、材料平板進行了計算,并用理論、數(shù)值、試驗的方法進行了驗證,但并未考慮流體負載的情況。
由于水下結(jié)構(gòu)物的流體負載影響不可忽略,為了明確湍流邊界層激勵下平板在不同流體介質(zhì)中振動響應(yīng)的相似性換算關(guān)系,以指導(dǎo)其在工程實際中的應(yīng)用,本文在上述研究的基礎(chǔ)上首先驗證了脈動壓力譜歸一化方法在不同介質(zhì)間的適用性,其次對考慮流固耦合的流激結(jié)構(gòu)響應(yīng)間的相似換算關(guān)系進行了假設(shè)和驗證,并給出了具體的公式以量化分析,為同種以及不同介質(zhì)流激結(jié)構(gòu)縮比模型的設(shè)計及響應(yīng)預(yù)報提供一定的參考。
1 理論分析
對于隨機聲學(xué)問題,因湍流脈動壓力激勵作用具有隨機性,各激勵力之間存在時空相關(guān)性,故隨機振動的研究更復(fù)雜。
根據(jù)隨機理論[6],湍流激勵下彈性結(jié)構(gòu)振動位移響應(yīng)的互功率譜密度表達式如下
Sw(x,ξ,ω)=?Spp(ξ′,ω)Hw(x,x′,-ω)·
Hw(x+ξ,x′+ξ′,-ω)dx′dξ′
(1)
式中:x=[x,y]為觀測點坐標;ξ=[ξx,ξy]代表兩個觀測點之間的空間距離向量;ω為圓頻率;Spp(ξ′,ω)為壁面脈動壓力互功率譜密度;Hw(x,x′,-ω)為結(jié)構(gòu)振動位移的單頻響應(yīng)函數(shù)。
位移單頻響應(yīng)函數(shù)的物理含義為:彈性結(jié)構(gòu)上的點x在位于x′處以圓頻率為ω的單位簡諧力作用下的振動位移響應(yīng)。
式(1)表明:求解振動位移響應(yīng)的關(guān)鍵在于得到湍流脈動壓力的互功率譜密度以及場點振動位移的單頻響應(yīng)函數(shù)。
1.1 平板湍流脈動壓力互功率譜密度
Corcos建立了經(jīng)典的湍流脈動壓力模型,湍流邊界層的脈動壓力在空間域上的互功率譜密度如下所示
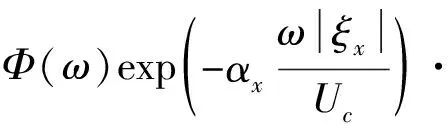
(2)
針對水中低馬赫數(shù)運動的結(jié)構(gòu)物,Hwang等指出:Corcos模型往往高估湍流邊界層壁面脈動壓力功率譜在低波數(shù)區(qū)的譜級,并提到一種改進型Corocs模型彌補了原型的不足。因此下文采用改進型Corcos模型

(3)
式中:Φ(ω)為平板湍流脈動壓力自功率譜密度,其選擇見1.2節(jié);ξ為激勵兩點空間距離的向量;ξx,ξy分別為兩點的流向和展向間距, 其中ξx=x2-x1,ξy=y2-y1,流向與展向相干函數(shù)衰減因子分別取αx=0.116,αy=0.7;i為虛數(shù)單位;U∞為遠方來流速度;Uc為邊界層在來流方向的遷移速度,Uc=βcU∞,βc根據(jù)試驗取0.6~0.8,本文取0.65。
1.2 脈動壓力自功率譜密度
Hwang等將湍流邊界層研究以來發(fā)展的壁面壓力譜的半經(jīng)驗?zāi)P团c試驗結(jié)果進行對比,其中Goody模型描述的壁面湍流脈動壓力自功率譜密度模型在風(fēng)洞、水洞等實驗場地的預(yù)報結(jié)果在各頻段對比良好。
對于壁面上的二維、零壓力梯度流,Goody給出壁面脈動壓力的自功率譜密度如下所示
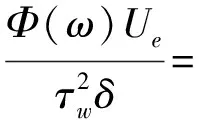
(4)
式中:Ue為壁面邊界層外緣速度,對于平板模型可近似取Ue=U∞;τw為壁面剪切應(yīng)力;δ為邊界層厚度;RT=(δ/Ue)/(υ/uτ);υ為流體運動黏度;uτ為壁面摩擦速度。
1.3 湍流激勵簡支平板的單頻響應(yīng)函數(shù)
考慮一充分發(fā)展的湍流作用在長寬分別為a、b的四邊簡支薄板上,薄板浸沒在密度為ρ0,聲速為c0的流體中,平板z>0的表面受到來流速度為U∞的湍流脈動壓力的激勵。如圖1所示,本文考慮遠場流速U∞與聲速c0相比可以忽略不計,因此不考慮對流運動對聲速的影響,可以認為聲速為一恒值。
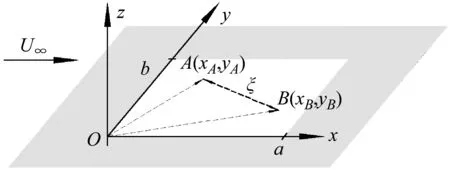
圖1 無限大剛性擋板上四邊簡支平板及坐標參考系Fig.1 Four-sided simply supported flat plate and coordinate reference system on infinite rigid baffle
用Corcos模型描述的脈動壓力功率譜作為輸入,將其視作一種外力激勵平板,流場-平板耦合振動的控制方程可寫成
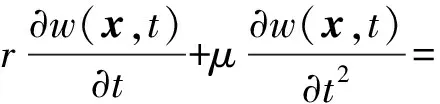
p(x,t)+pa(x,0+,t)-pa(x,0-,t)
(5)
式中:w(x,t)為簡支板的振動位移函數(shù);D為平板的彎曲剛度,D=Eh3/12(1-υ2);υ為泊松比;r為損耗因子;μ為平板的面密度;t為時間;p(x,t)為湍流邊界層的脈動壓力;pa(x,0+,t)為平板z>0表面的聲壓;pa(x,0-,t)為平板z<0表面的聲壓。結(jié)構(gòu)振動位移的單頻響應(yīng)函數(shù)與簡支板的振動位移函數(shù)之間滿足以下關(guān)系
Hw(x,x′,-ω)eiωt=w(x,t)
(6)
湍流邊界層脈動壓力p(x,t)表達式如下
p(x,t)=δ(x-x′)eiωt
(7)
平板振動引起的聲壓滿Helmholtz波動方程
(8)
平板與流場耦合的連續(xù)性條件如下所示
(9)
根據(jù)文獻[7],流體負載平板的振動位移函數(shù)w可表示如下
(10)
式中:Wmn(ω)為模態(tài)參與系數(shù);αmn(x)為簡支板在真空中歸一化的固有振型函數(shù)。在(0,0)≤x≤(a,b)的空間域中,其表達式為
(11)
固有振型函數(shù)αmn(x)對應(yīng)的本征頻率如下
(12)
定義傅里葉變換對
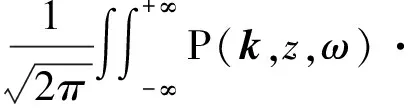
exp[i(k·x+ωt)]dkdω
(13)

exp[-i(k·x+ωt)]dxdt
(14)
式中:k=[kx,ky],由式(6)及聲場輻射條件得
(15)


exp[-i(k·x+ωt)]dxdt
(16)
根據(jù)以上公式,由附錄A的推導(dǎo),可得平板振動位移的單頻響應(yīng)函數(shù)Hw的表達式為

αmn(x)αqs(x′)
(17)
平板上某一點(x,y)的速度可以表示為v(x,t)=?w(x,t)/?t,結(jié)合式(1)、式(6)可得平板振動位移與振動速度互功率譜間的關(guān)系如下
Sv(x,ξ,ω)=ω2Sw(x,ξ,ω)
(18)
結(jié)合式(1)、式(3)和式(18),可得平板振動速度的互功率譜密度

?Spp(ξ′,ω)αkl(x′)·α(x′+ξ′)dx′dξ′
(19)
通過將式(19)中的ξ設(shè)為0,可以得到平板給定節(jié)點的振動速度自功率譜密度函數(shù),如下所示
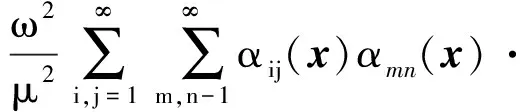
αkl(x)·α(x+ξ)dxdξ
(20)
平板振動的平均速度響應(yīng)可用如下面積平均來表示,根據(jù)模態(tài)振型的正交性,積分可以簡化如下

(21)
式中:Zmmnn(ω)為阻抗,其表達式如下
Zmmnn(ω)=μCmnmn(ω)
(22)
其中N和M為模態(tài)截斷數(shù),式(21)中的受納函數(shù)Amnmn(ω),其積分形式如下所示

αmn(x)αmn(x+ξ)dxdξ
(23)
式(23)中的積分,可采用文獻[8]中的方法并結(jié)合數(shù)值積分計算。得到流激平板結(jié)構(gòu)振動響應(yīng)的表達式,接下來考慮其存在的相似關(guān)系。
1.4 不同流場介質(zhì)平板響應(yīng)相似性準則
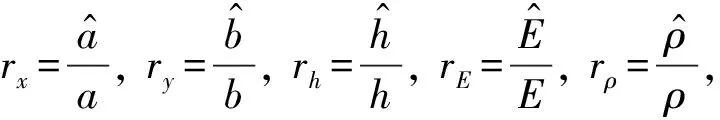
(24)
對于本文所研究的流激響應(yīng)問題,若原始模型與相似模型外流場的雷諾數(shù)Re較大的時候,流動進入紊流粗糙區(qū),此時流動的阻力大小與Re無關(guān),只與相對粗糙度有關(guān),這個流動范圍稱為自模區(qū)。若原型與模型的兩個流動都處于自模區(qū),則只做到幾何相似,而不必Re相等,就自動實現(xiàn)了動力相似。本文研究的流動均處于自模區(qū)。
忽略湍流邊界層時均壓力對平板變形量的影響。采用模態(tài)疊加法計算湍流邊界層激勵下平板響應(yīng),真空中平板振動平均速度的一種相似性準則在文獻[10]的基礎(chǔ)上出
(25)
其中,第一條假設(shè)約束了相似平板的長寬幾何相似,第二條假設(shè)約束了相似平板的計算頻段的縮比因子需要與振型的本征頻率的縮比因子保持一致,第三條假設(shè)在前兩條假設(shè)的基礎(chǔ)上給出了遠場流速如何設(shè)計,其中cs為一常數(shù)。
本文考慮流體負載的計算方法,同樣采用模態(tài)疊加法。為觀察這套相似性準則是否依然適用,考慮累加項中的受納函數(shù)Amnmn(ω),將式(24)及式(25)代入式(23),當(dāng)計算頻率較高時,可得受納函數(shù)的縮比因子如下所示
(26)
再考慮累加項中阻抗項Zmmnn(ω),結(jié)合式(22)與式(25),得到阻抗縮比關(guān)系見附錄B。
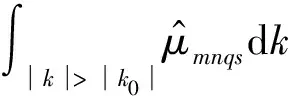
兩個積分項的展開如附錄C所示:根據(jù)附加質(zhì)量項與附加慣性項顯示的被積函數(shù)和積分上下限的特征,引入第四條假設(shè)
(27)
第四條假設(shè)引入了湍流介質(zhì)的聲速,根據(jù)式(25)中的第三條假設(shè),實際上約束了流場聲速與流速的縮比因子必須相等。將假設(shè)(27)代入到式(22)的積分項中,同時結(jié)合簡化后阻抗的縮比關(guān)系的特征,引入第五條假設(shè)
(28)
第五條假設(shè)引入了湍流介質(zhì)的密度,表明湍流介質(zhì)與平板長寬尺度的縮比因子之積必須與平板面密度縮比因子相等。將式(27)與式(28)的假設(shè)代入式(22),阻抗縮比關(guān)系可簡化為下式
(29)
(30)
式(30)實際上約束了在外流場給定情況下,平板材料必須滿足的條件。結(jié)合式(25)、(26)、(29),可以得到用湍流脈動壓力自功率譜密度函數(shù)歸一化的平板彎曲振動位移平均速度響應(yīng)間的縮比關(guān)系
(31)
對式(31),要得到平板彎曲振動位移平均速度響應(yīng)的縮比關(guān)系,需要考慮脈動壓力自功率譜的相似性。
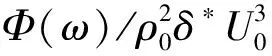
將脈動壓力自功率譜密度按Hwang所給方法歸一化處理之后得到平板彎曲振動位移平均速度響應(yīng)間的縮比關(guān)系
(32)
需要注意的是,這些相似性準則的推導(dǎo)是在假定Corcos模型中的系數(shù)αx,αy不隨頻率改變的前提下進行的,在對相似平板通過相似性準則得到縮比的湍流流速之后,平板的計算頻率和響應(yīng)需要依據(jù)公式進行縮比。
本文推導(dǎo)相似換算方法,是在以下五條假設(shè)的基礎(chǔ)上建立的
(33)
對于各向同性的相似平板和原型平板,如果它們均為四邊簡支邊界條件,相似換算的整個流程可總結(jié)如下:
(1) 若平板的長寬幾何相似,則兩個平板間就具備了相似的前提。在選定外流場的前提下,根據(jù)式(30)可得相似平板的材料應(yīng)滿足的特征,確定好相似平板的材料后,根據(jù)假設(shè)5設(shè)計相似平板的長寬與厚度。
(3) 最后計算縮比模型振動速度響應(yīng)的縮放因子,對相似平板的計算頻率和響應(yīng)分別按照式(25)與(32)進行縮放,即可實現(xiàn)對原型平板響應(yīng)的預(yù)報。
綜上,考慮流體負載的情況下,可通過對尺寸、材料屬性、流速等的配合,可以實現(xiàn)不同流體介質(zhì)下模型響應(yīng)間的相似換算。
2 算例驗證與分析
針對1.4節(jié)提出的不同流體介質(zhì)中壁面湍流脈動壓力自功率譜密度歸一化與四邊簡支板流激響應(yīng)的相似準則問題,用以下算例進行了驗證。
2.1 流激響應(yīng)相似性準則驗證
為了驗證并說明1.4節(jié)提出的相似性換算關(guān)系的適用范圍,選取幾種具有典型縮比關(guān)系的平板,它們各自的尺寸和相應(yīng)的縮比因子如表1所示。其中平板P0被選作原型平板,其材料為鋼,鋼材參數(shù)如表2所示,外流場為水;P1為長寬厚等比例縮放的鋼板,外流場為水;P2代表厚度與長寬縮比因子不等的平板,外流場同樣為水,以上三種方案的湍流邊界層在流經(jīng)平板前緣之前經(jīng)過長為1 m,表面粗糙度為0.000 2的區(qū)域;P3代表厚度與長寬縮比因子不等的平板,外流場為空氣,流場流經(jīng)平板前緣之前經(jīng)過長為1 m,表面粗糙度為0.002的區(qū)域。其中P2~P3模型的密度和彈性模量暫不考慮實際情況,以上四種方案均認為湍流邊界層在平板上的脈動壓力與湍流在平板前粗糙區(qū)域充分發(fā)展后的脈動壓力保持一致。經(jīng)檢驗以上流動均已進入自模區(qū)[16]。

表1 平板P0~P3的參數(shù)與相應(yīng)的縮比因子
理論分析部分假定平板均為四邊簡支的邊界條件,對于原型平板,假定遠方來流速度為10 m/s,計算中取橫、縱半波波數(shù)均為15,在計算頻段范圍,這個橫、縱半波波數(shù)經(jīng)過了模態(tài)收斂性驗證,結(jié)構(gòu)響應(yīng)可計算到1 500 Hz,剩余平板采用了同樣的半波數(shù)組合,并假定泊松比和結(jié)構(gòu)阻尼不隨頻率改變。表2給出了P0~P3平板的參數(shù)與縮比因子。
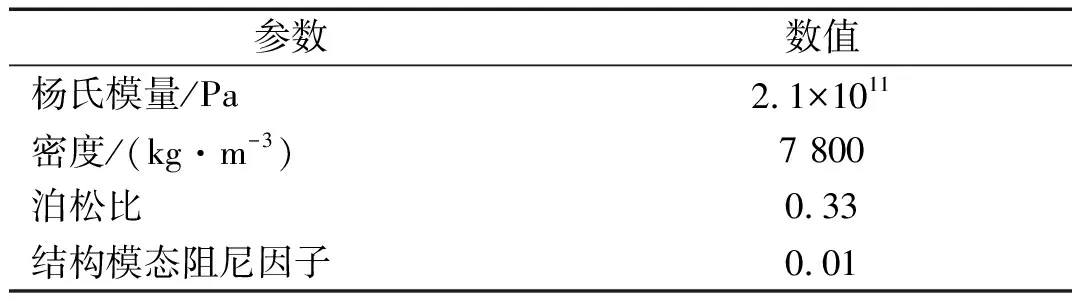
表2 鋼材材料參數(shù)
平板區(qū)域內(nèi)以邊界層厚度以及壁面剪切應(yīng)力均以平板前緣為準,可以驗證以上流激響應(yīng)方案均已進入紊流粗糙區(qū)。根據(jù)文獻[17],各方案紊流粗糙區(qū)邊界層時均參數(shù)如表3所示。
首先對脈動壓力自功率譜密度的歸一化方法進行驗證,根據(jù)表2所給參數(shù),以ω為橫坐標,脈動壓力自功率譜為縱坐標,對比四種方案下的湍流脈動壓力自功率譜特性,如圖2所示。
運用1.4節(jié)描述的中、低頻段脈動壓力歸一化處理方法,得到縮放后的脈動壓力自功率譜密度對比如圖3所示。

表3 邊界層時均參數(shù)計算結(jié)果
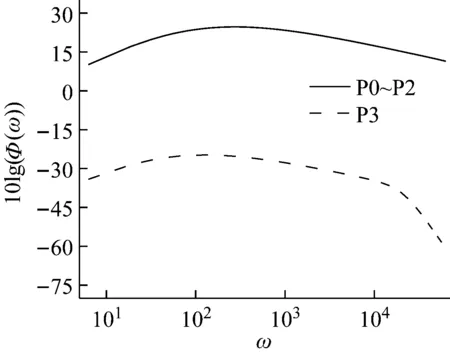
圖2 脈動壓力自功率譜密度(未縮放)Fig.2 Pulsating pressure self-power spectral density (unscaled)
經(jīng)檢驗,本文算例的脈動壓力自功率譜密度函數(shù)在所屬頻段應(yīng)用該縮放尺度可以實現(xiàn)歸一化。
依據(jù)表1所給參數(shù)中的長寬、厚度、材料屬性、流速等作為輸入,對尺寸、材料、外流場均變化的平板P0~P3的響應(yīng)分別進行計算,橫坐標的計算頻率保持0~1 500 Hz,所得振動速度響應(yīng)對比如圖4所示。
原型平板的計算頻率和響應(yīng)保持不變,對相似平板的計算頻率和響應(yīng)分別按照式(33)與(32)進行縮放。得到縮放后振動速度響應(yīng)對比如圖5所示。
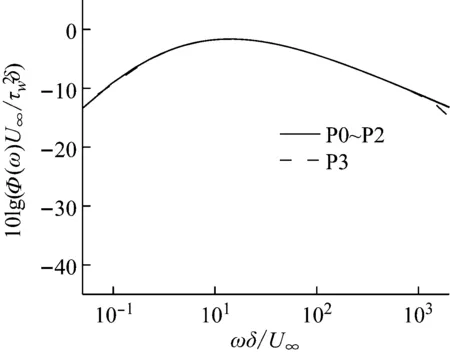
圖3 脈動壓力自功率譜密度(用中、低頻的縮放尺度)
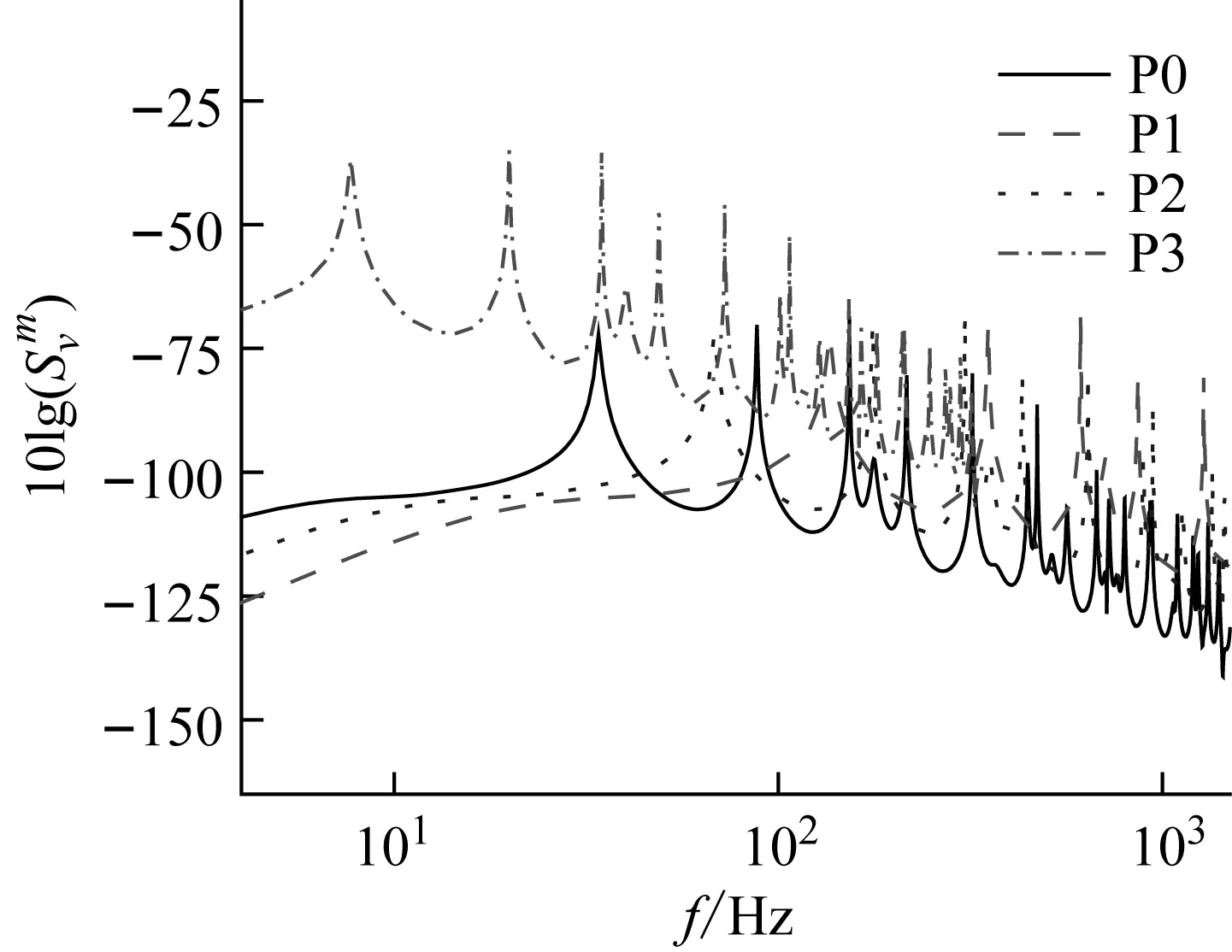
圖4 平板平均振動速度(P0~P3未縮比)
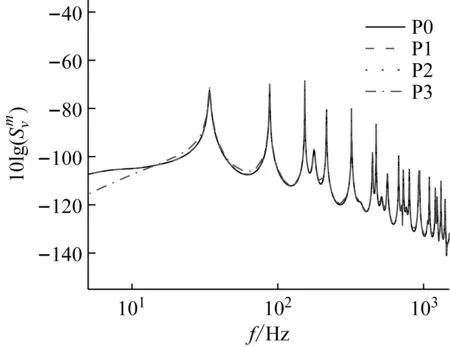
圖5 平板平均振動速度(P0~P3縮比換算后)
通過圖4、圖5的對比可知:尺寸不同、材料不同、外流場不同的平板速度響應(yīng)一般各不相同。但這些平板的響應(yīng)經(jīng)過尺寸設(shè)計和相似換算,可以得到與原型平板的響應(yīng)結(jié)果的重合。
3 結(jié) 論
本文結(jié)合改進的Corcos模型描述的脈動壓力激勵下平板振動速度響應(yīng)的特點,將平板振動響應(yīng)的互功率譜密度分解為湍流脈動壓力互功率譜密度函數(shù)和結(jié)構(gòu)振動位移的單頻響應(yīng)函數(shù)。
對于壁面湍流脈動壓力自功率譜密度,驗證了脈動壓力歸一化的方法在不同流體介質(zhì)間的適用性。對于結(jié)構(gòu)振動位移的單頻響應(yīng)函數(shù),考慮其相似性提出了五個假設(shè),在此基礎(chǔ)上推導(dǎo)了相似換算方法,給出了速度響應(yīng)換算的具體公式。最后對幾類平板彎曲振動的平均速度響應(yīng)進行了計算與換算,通過對比,得到了以下結(jié)論:
(1) 湍流壁面脈動壓力自功率譜密度的歸一化方法,在不同流體介質(zhì)間有適用性。
(2) 同種介質(zhì)湍流脈動壓力激勵下,材料相同,幾何等比例縮放的平板,可以通過流速和頻段的設(shè)計,依據(jù)本文的方法實現(xiàn)相似換算。
(3) 同種介質(zhì)湍流脈動壓力激勵,幾何不全相似的平板,以及不同介質(zhì)湍流脈動壓力激勵下的平板,其振動響應(yīng)在理論上可以依據(jù)本文方法實現(xiàn)相似換算。但模型材料受外流場密度與平板面密度的限制,工程實現(xiàn)難度大。該理論在不同外流場介質(zhì)中的應(yīng)用可為之后的研究提供一定的參考。
本文中Corcos模型激勵下平板響應(yīng)的換算是在泊松比、結(jié)構(gòu)阻尼、Corcos模型參數(shù)等不隨頻率變化的前提下完成的,對于試驗 的復(fù)雜情況,應(yīng)作專門的研究,對相似性準則進行修正。
附錄A 平板振動位移的單頻響應(yīng)函數(shù)Hw推導(dǎo)
由式(9)、式(10)、式(13)、式(14)和式(15)可得聲壓的表達式為:
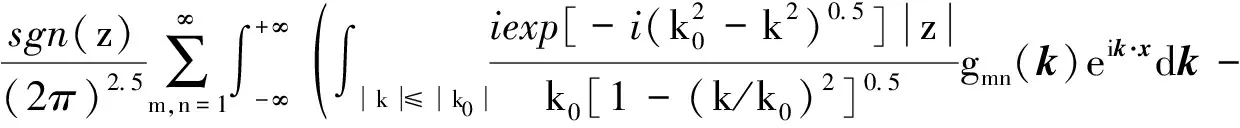
(A.1)
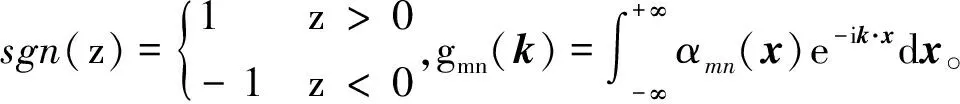
將式(10)、式(13)、式(15)代入到總控方程中,并對方程兩邊進行傅立葉變換和正交變換,可得耦合振動控制方程為:
(A.2)

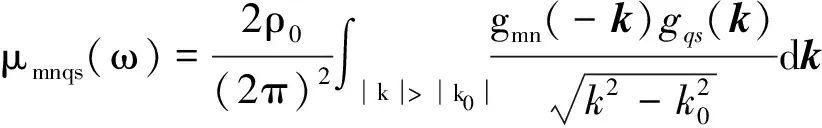
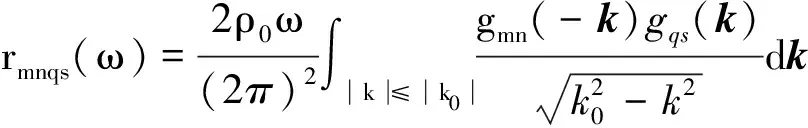
定義:
(A.3)

附錄B 阻抗縮比因子
(B.1)
附錄C 附加質(zhì)量項與附加慣性項的積分展開
附加質(zhì)量項積分展開:
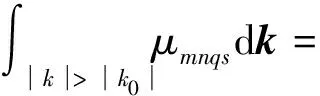
(C.1)
附加慣性項積分展開:

(C.2)

