懸索橋吊索疲勞荷載效應分析
任宇揚
(河北省交通規劃設計研究院有限公司 石家莊市 050000)
0 引言
懸索橋[1-2]是利用主纜和吊索(吊桿)作為加勁梁的懸掛體系,將上部荷載作用傳遞到索塔、錨錠的橋梁形式。懸索橋傳力路徑:荷載由加勁梁傳遞給吊索,再由吊索傳至主纜,再由主纜傳至錨錠。主纜是懸索橋的主要承重構件,支承在橋塔上,錨固于錨錠。吊索(吊桿)是懸索橋的傳力結構,通過它能將活載和加勁梁自重等荷載傳給主纜。吊索受到軸向拉力的大小很大程度上影響了主纜在成橋階段的線形,同時也影響了加勁梁的恒載彎矩,是分析懸索橋成橋階段的重要參數。吊索由索體、錨頭和索的防腐蝕系統三部分組成。索體主要有鋼絞線、平行鋼絲等結構型式。相較于鋼絞線吊索,平行鋼絲吊索具有明顯的優勢:工廠預制化高,工藝成熟,質量穩定;冷鑄錨錨固可靠;鋼絲受力均勻;鋼絲軸向剛度大,材料利用率高;經濟效益好。因此目前國內外大跨度懸索橋吊索主要采用鍍鋅高強平行鋼絲。
隨著科學技術的發展,懸索橋吊索平行鋼絲的強度不斷提高。但鋼絲的延性變差,脆性增加,抗疲勞性能變差,易發生疲勞斷裂。近年來懸索橋跨徑增大、自重降低、活載增大,導致疲勞應力幅增大,吊索中平行鋼絲的疲勞斷裂風險日益嚴重。懸索橋吊索的耐久性問題應該得到廣泛的重視[3]。
以廣東省某跨海大橋主航道橋——雙塔雙索面懸索橋為例,建立空間桿系的有限元模型,對懸索橋吊索疲勞荷載應力幅進行分析,根據實橋調查車輛荷載統計特性,用蒙特卡洛隨機抽樣法模擬的車流加載,并根據各國規范編制雨流計數法程序對吊索的疲勞損傷度進行數值模擬分析,并以模擬車流、AASHTO、BS5400、EUROCODE疲勞荷載模型進行比較,計算每一種規范下的等效應力幅進行疲勞分析。
1 工程概況
如圖1所示,本懸索橋全長4600m,主跨888m,為地錨式懸索橋[4-5],東側邊跨302.0m,西側邊跨345.5m,矢跨比1/10.5。承臺以上塔高147.55m,橋面以上89.86m,主纜的橫向中心距為33.0m,每根主纜由110股索股組成,每根索股由127絲Φ5.2mm的鍍鋅高強鋼絲組成,鋼絲極限抗拉強度為1670MPa。加勁梁為扁平閉合流線型鋼箱梁,橋梁寬度為35.6m。橋軸中心線處梁高3.012m。鋼箱梁主體鋼材采用SM490C型鋼材。
本橋計算分析采用有限元分析程序ANSYS。建立三維桿系魚骨梁模型,如圖2所示[6]。主纜和拉索采用link10單元模擬;加勁梁、橋塔均采用程序內的beam188單元模擬;加勁梁材料為SM490C鋼材,彈性模量E=2.1×105MPa,泊松比取0.3;剛臂采用beam188單元模擬,彈性模量取加勁梁模量的1000倍。橋塔底部全固結處理;采用橫橋向、縱橋向、扭轉的耦合約束來模擬橋梁支座。地錨端采用固結處理。全橋一側共72根吊索,半跨為36根吊索。從橋塔向跨中依次編號:東側E1~E36;西側W1~W36[7]。

圖1 懸索橋總體布置圖(單位:cm)
圖2 懸索橋全橋有限元模型
2 吊索疲勞荷載模型
根據本橋附近的交通資料數據分析得到本橋車輛信息(表1),并可以得到懸索橋的車輛概率密度分布,應用蒙特卡洛算法,設隨機變量Y,累積分布函數為Y=F(X)。則有Y~R(0,1),因此X=F-1(Y)。這樣可以利用程序產生[0, 1]上的隨機數ξi(i=1,2……n),進而得到Xi(i=1,2……n)。因此只需通過統計調查獲得車輛類型、車重、軸重、車輛間距的累積分布函數,就可以通過產生在[0, 1]上的隨機數列來模擬出車流。車輛荷載譜如圖3所示。以一天(24h)通過本橋的六車道車流,作為一個車隊樣本[8]。
假設任意兩輛車的時間間隔t,其服從泊松分布F(t),根據交通量調查資料,本橋的平均車速v=23.5m/s,車輛平均時間間隔為μt=17.0s,車間距樣本x可由下式求得,其中F(t)為服從[0,1]均勻分布的隨機變量。
x=-vμtln[1-F(t)]
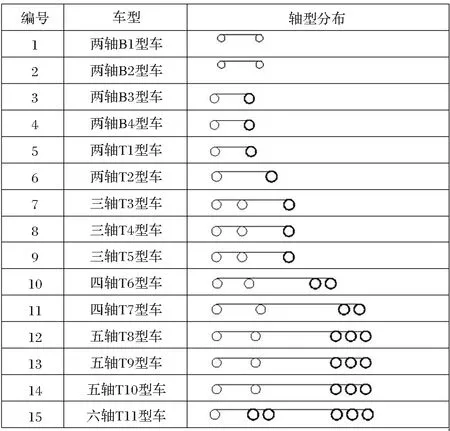
表1 本橋車輛類型匯總表
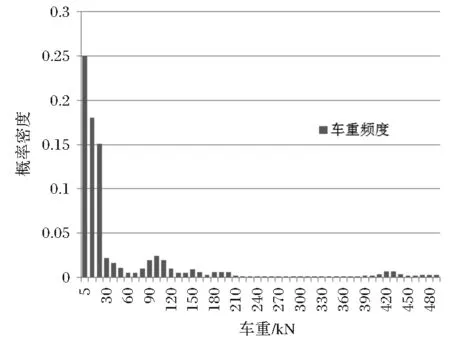
圖3 本橋車重荷載譜
3 吊索影響線和車隊加載
本橋的吊索編號如圖3由東側塔根(左)向跨中為E1~E36;西側塔根(右)向跨中為W1~W36。
對于空間有限元全橋模型的吊索應力影響線加載(中軸線加載)[9]。可以得出1~36號吊索的應力影響線(1號為邊索靠近橋塔,36號為中間索靠近跨中)。發現吊索的應力影響線較長,影響范圍在400m左右(本橋主跨888m),但是數值較大的區域并不是很長,只在本吊索附近開始級數突變。而各個吊索的應力幅值的最大值,從1號至36號,隨著吊索的長度的減小而逐漸增大。在E36(W36)號處有應力幅最大,其值為16.8MPa,如圖4所示。因此本懸索橋位于跨中附近長度較短的吊索應力幅值較大。

圖4 懸索橋吊索應力幅最大值匯總圖
在考慮內外車道加載單位力的情形下,分析36號吊索影響線發現,當在靠近拉索的外車道加載時的應力幅值最大,最不利,其數值為25.2MPa。在遠離拉索的外車道加載的應力幅值相對較小。
采用兩種方法模擬車隊荷載:
(1)將一輛車的重量簡化為一個集中荷載,不考慮軸重分布,采用蒙特卡洛算法模擬車重和車距;
(2)根據表1的不同車型比例,考慮軸重分布并應用蒙特卡洛算法模擬車重和車距。
采用上述兩種車隊荷載進行影響線加載,用雨流計數法得到吊索的應力幅譜,本橋36號吊索的應力幅值譜如圖5所示。分析可知,兩種加載方式下36號索的應力幅值幅相差不大于10%,由上述結果可知,軸距分布對吊索應力幅的影響較小,可以將車輛荷載簡化為一個集中荷載。

圖5 36號吊索應力幅值譜
4 拉索疲勞效應
采用本懸索橋交通量的模擬車流模型、AASHTO標準疲勞車、BS5400標準疲勞車、EUROCODE疲勞車模型3加載可以得到的100年2×106次的等效應力幅,如表2所示。AASHTO疲勞車加載,36號吊索所得等效應力幅值與模擬車隊加載的計算結果偏差在4.7%。BS5400規范疲勞車模型加載所得等效應力幅值與模擬車隊的計算結果偏差在3.6%,歐規疲勞車模型加載得到的數據結果與模擬車隊相差達38.8%,結果是偏安全的。

表2 36號吊索等效應力幅匯總表
5 結語
基于廣東省某跨海懸索橋,采用有限元方法,對懸索橋吊索的疲勞荷載效應進行分析。主要結論如下:
(1) 本懸索橋吊索的應力影響線較長,影響范圍約為400m(橋梁主跨888m)。
(2) 軸重分布對于此類影響范圍較長的懸索橋吊索應力影響線的應力譜產生的影響較小。可知車重分布對懸索橋吊索應力譜的影響較大。軸距對應力幅的影響較小,可以將車輛荷載簡化為一個集中力荷載。
(3) 懸索橋吊索疲勞設計中建議:根據該橋的交通資料分析得到模擬車隊,采用模擬車隊荷載為疲勞荷載模型。不建議簡單套用國外規范的疲勞荷載計算吊索疲勞荷載效應。

