重力場模型對Swarm衛星精密定軌的影響分析

方文豪，孔巧麗，李長松，張德志，張令綱，王田發

（ 山東科技大學 測繪與空間信息學院, 山東 青島 266590 ）

0 引 言

歐洲航天局(ESA)已于2013年11月22日成功發射Swarm衛星[1]，Swarm星座是ESA首個用于測量來自地球核心、地幔、地殼、海洋、電離層等區域磁場信息的對地觀測衛星星座[2]. 該星座包括A、B、C三顆小衛星，分別運行在2個軌道面上. 其中Swarm-A和Swarm-C衛星在高度450 m，傾角87.4°的極軌道面運行，而Swarm-B衛星在高度530 m，傾角88°的極軌道面飛行[3].

自星載GPS觀測技術成功應用于TOPEX/Poseidon衛星[4]以來，該技術已成為低軌衛星精密定軌最主要的技術手段. 常見的低軌衛星精密定軌方法有動力學定軌、簡化動力學定軌以及運動學定軌. 采用動力學法能夠獲得連續的衛星軌道坐標及速度，但難以精確測定大氣阻力、太陽光壓以及地球返照射壓等攝動力，因此衛星的定軌精度有待進一步提高[5].運動學法利用星載GPS雙頻觀測值對低軌衛星進行精密定軌，不考慮低軌衛星的受力情況和天氣狀況，精度不受低軌衛星軌道高度的影響[6]. 但這種方法的定軌精度與GPS衛星的幾何圖形結構有很大關系，因此，其定軌精度并不穩定[7]. 簡化動力學法融合了動力學法和運動學法的優點，采用過程附加參數來吸收動力學模型誤差與未被模型化的誤差，通過確定幾何信息與動力學模型之間的最優權來減弱動力學模型對精度的影響，從而實現幾何信息和動力學信息的最佳匹配[8-9]. 隨著星載GPS測軌技術的迅速發展，利用簡化動力學法進行低軌衛星精密定軌獲得了廣泛的應用. 文獻[7]采用星載GPS觀測數據，對Swarm衛星進行精密定軌，定軌精度為4～7 m. 文獻[10-11]采用簡化動力學法對GOCE衛星進行精密定軌，軌道精度優于2 m. 文獻[12]利用星載GPS雙頻觀測值，對GRACE衛星進行簡化動力學定軌，GRACEA與GRACE-B的軌道精度均達到2.5 m. 文獻[13]將簡化動力學定軌應用于TOPEX/Poseidon衛星，其定軌精度優于3 m. 文獻[14]利用BERNESE5.2對Jason-3衛星進行精密定軌，精度優于3.6 m. 文獻[15]運用簡化動力學法對HY-2A衛星進行精密定軌，其徑向定軌精度達到2 m.

在對Swarm衛星進行簡化動力學定軌過程中，衛星所受到的攝動力模型會影響其定軌精度，其中地球重力場模型的精度對定軌精度的高低具有較大的影響. 不同的地球重力場模型和不同階次的重力場模型會對衛星定軌精度產生不同的影響. 本文利用Swarm衛星星載GPS雙頻觀測值和簡化動力學法，對Swarm衛星精密軌道進行解算. 解算軌道的過程中引入適當的偽隨機脈沖參數，并將這些參數與其他參數一起估計. 重點研究了GOCO06s地球重力場模型展開到不同階次時的Swarm衛星簡化動力學定軌精度，并且探討了采用100階次的PGM2000a、EIGEN-2、EGM2008和GECO重力場模型對Swarm衛星軌道的影響，得出了一些有益的結論.

1 簡化動力學定軌理論

簡化動力學定軌方法是低軌衛星精密定軌的常用方法. 該方法能夠充分利用星載GNSS觀測數據和動力學模型的優點實現低軌衛星的精密定軌. 為了減少待求參數的個數，一般會引入經驗參數或偽隨機脈沖參數，從而吸收動力學模型誤差和未被模型化的攝動力誤差. 該方法可以保證動力學模型對衛星軌道的約束，從而有效提高低軌衛星精密定軌精度[16].

低軌衛星在軌道上運行時會受到多種攝動力的作用，從而導致衛星軌道比較復雜. 這些攝動力包括地球非球形攝動、地球潮汐攝動、相對論效應、多體攝動等保守攝動力和大氣阻力、太陽光壓、地球返照壓等非保守攝動力. 在慣性系中，低軌衛星運動方程表示為[5]

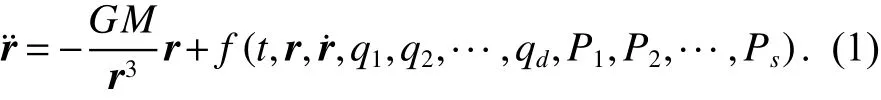
2 數據來源和處理策略

本文采用歐空局(ESA)提供的1 s采樣間隔的星載GPS雙頻觀測數據，歐洲定軌中心(CODE)提供的15 min采樣間隔的GPS衛星精密星歷文件、地球自轉參數文件和30 s采樣間隔的精密衛星鐘差文件. 觀測數據的時間跨度為2020-08-01—05，采用的軟件為BERNESE5.2. 偽隨機脈沖和分段常數加速度的時間間隔均設置為6 min，偽隨機脈沖先驗標準差設置為10-6m/s，分段常數加速度先驗標準差設置為10-9m/s. 基于簡化動力學定軌法，利用最小二乘法將偽隨機脈沖參數和其他軌道參數一起進行解算，從而得到衛星精密軌道. 表1為Swarm衛星簡化動力學定軌模型及處理策略.

表1 Swarm衛星簡化動力學定軌模型及處理策略

3 Swarm衛星定軌結果分析

采用外符合法進行軌道精度驗證，參考軌道為ESA提供的科學軌道. 為了分析不同階次的GOCO06s地球重力場模型對Swarm系列衛星定軌精度的影響，本文將GOCO06s地球重力場模型分別展開到30階、50階、80階、100階及120階，利用BERNESE5.2軟件基于簡化動力學方法采用上述不同階次的重力場模型解算Swarm衛星精密軌道. 表2為定軌精度統計信息，采用30、100及120階次GOCO06s地球重力場模型解算的Swarm-A、Swarm-B和Swarm-C衛星的簡化動力學軌道與參考軌道差異分別如圖1～3所示.

圖1 采用30階次GOCO06s地球重力場模型解算的軌道與參考軌道差異

表2 采用不同階次的GOCO06s地球重力場模型解算的衛星軌道與參考軌道差值 m

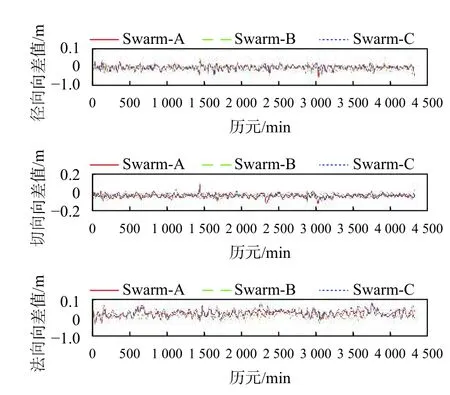
圖2 采用80階次GOCO06s地球重力場模型解算的衛星軌道與參考軌道差異

由圖1～3和表2可知：采用30階次的GOCO06s地球重力場模型解算的Swarm衛星軌道精度均保持在分米級，無法滿足低軌衛星精密定軌的需求. 當GOCO06s地球重力場模型的階次保持在30～100階次時，隨著重力場階次的不斷增加，Swarm-A、Swarm-B和Swarm-C衛星在徑向、切向、法向上的定軌精度越來越高，而在100階次與120階次的定軌精度相當，說明在100階次定軌精度基本穩定. 采用120階次的GOCO06s地球重力場模型進行簡化動力學定軌，Swarm-A衛星的徑向、切向、法向以及三維方向上的定軌精度分別為0.009 m、0.018 m、0.014 m和0.024 2 m，Swarm-B衛星的定軌精度分別為0.009 m、0.016 m、0.013 m和0.023 m，Swarm-C衛星的定軌精度分別為0.008 m、0.016 m、0.015 m和0.024 m. 因此可以看出，三顆Swarm衛星的定軌精度均優于3 cm.

圖3 采用120階次GOCO06s地球重力場模型解算的衛星軌道與參考軌道差異

此外，采用100階次的PGM2000a、EIGEN-2、EGM2008以及GECO重力場模型分別對Swarm衛星進行定軌，以此來考察不同的地球重力場模型對Swarm衛星定軌精度的影響. 分別采用100階次的各重力場模型對Swarm-A、Swarm-B和Swarm-C衛星進行精密定軌，定軌結果與參考軌道差值的均方根(RMS)統計信息見表3.

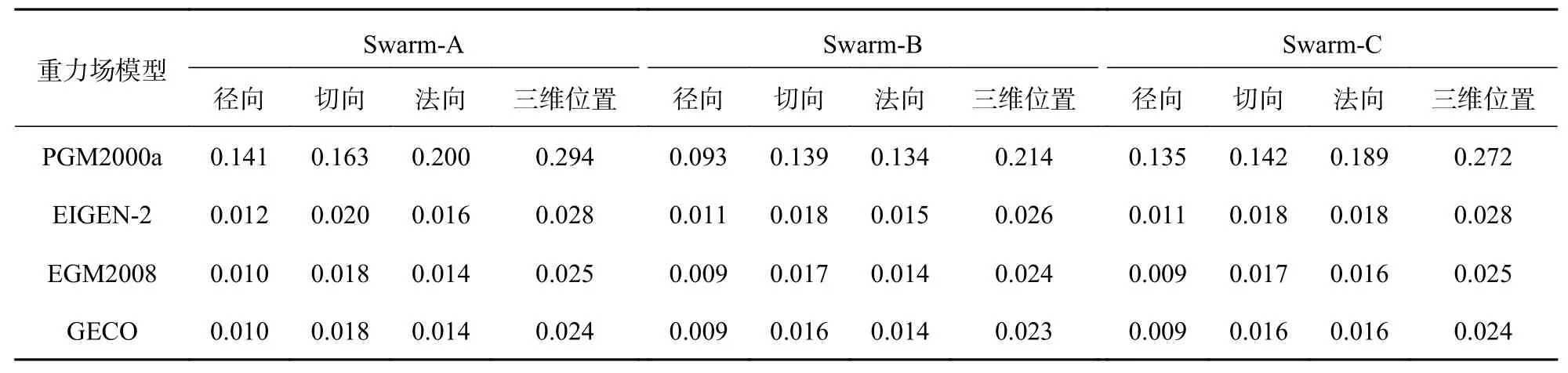
表3 100階次的不同重力場模型解算的Swarm衛星定軌結果與參考軌道差值RMS m

由表3可知，利用100階次的PGM2000a重力場解算出的三顆Swarm衛星軌道精度均在分米量級，而采用100階次的EIGEN-2、EGM2008以及GECO重力場模型得到的軌道精度均在厘米量級，定軌精度優于3 cm. 由此可以看出，采用EIGEN-2、EGM2008以及GECO重力場模型得到的定軌精度明顯均優于PGM2000a. 由表2和3可知，相比于100階次的PGM2000a、EIGEN-2、EGM2008以及GECO重力場模型，采用100階次的GOCO06s、GECO和EGM2008模型解算出的Swarm衛星軌道精度相對較高. 所以，為了保證解算出的Swarm衛星軌道具有較高的精度和穩定性，實際解算衛星軌道時，需要考慮衛星的在軌運行高度等情況，合理選取地球重力場模型及其階數.

4 結束語

本文采用星載GPS雙頻觀測數據對Swarm衛星進行簡化動力學定軌，在軌道解算過程中加入偽隨機脈沖參數. 詳細研究了GOCO06s地球重力場模型分別展開到30階、50階、80階、100階以及120階時的Swarm衛星簡化動力學定軌精度，對比了采用100階次的PGM2000a、EIGEN-2、EGM2008以及GECO重力場模型時解算的Swarm衛星軌道精度，得到結論如下：

1)當GOCO06s地球重力場模型從30階次逐步展開到100階次時，解算出的Swarm-A、Swarm-B和Swarm-C衛星軌道在徑向、切向、法向上的精度越來越高，在重力場模型階次大于100時，軌道精度穩定，3顆衛星的精度均優于3 cm.

2)采用100階次的PGM2000a重力場模型解算出的衛星定軌精度在分米量級，而利用同階次的EIGEN-2、EGM2008以及GECO重力場模型解算的軌道精度均保持在厘米級，其中采用GECO和EGM2008模型解算出的軌道精度與GOCO06s解算出的軌道精度相當.

3)實際解算衛星軌道時，為了得到較高的定軌精度，需要合理選取地球重力場模型及其階次.