顧及有色噪聲影響的青海地區應變場分析

張幸，魏冠軍

（ 1. 蘭州交通大學 測繪與地理信息學院, 蘭州 730070；2. 地理國情監測技術應用國家地方聯合工程研究中心, 蘭州 730070；3. 甘肅省地理國情監測工程實驗室, 蘭州 730070 ）

0 引 言

目前，中國大陸構造環境監測網絡(CMONOC)積累了大量連續運行參考站(CORS)的原始觀測數據，為研究青海地區的板塊運動、地殼形變、速度場模型等提供了十分重要的基礎數據[1]. 由于觀測數據中存在的有色噪聲(CN)降低了測站運動參數的估計精度，且不同地區的噪聲特性差異明顯[2-7]，因此，選擇合適的噪聲模型來研究連續站的穩定性及地表規律具有重要意義. ZHANG等[5]在加利福尼亞南部地區時間序列研究中引入噪聲分析，發現時間序列噪聲具有白噪聲+閃爍噪聲(WN+FN)的特征. 蔣志浩等[6]的研究表明，CORS站坐標時間序列具有WN、FN和隨機漫步噪聲(RW)的噪聲特征. 管雅慧等[7]對云南地區CMONOC連續站坐標時間序列進行分析，認為時間序列觀測數據超過5年時，噪聲模型才能逐漸趨于穩定. 王偉等[8]基于CMONOC觀測數據獲得了青藏高原的水平運動速度場及應變場，認為該地區應變場的整體分布特征與該地區活動構造的空間分布及地震活動十分一致. 綜合上述研究表明，應變場分析應當選擇較長時間段的觀測數據并顧及CN的影響.

針對目前青海地區應變場研究中未顧及CN的影響且未對較長時間段(10年或以上)坐標時間序列噪聲進行分析，本文通過分析青海地區14個CMONOC連續站2010—2020年的時間序列數據，分別確定了3個方向的最優噪聲模型，得到國際地球參考框架(ITRF)下經最優噪聲模型改正后的青海速度場，并基于修正后的速度場建立整體旋轉與線性應變模型來分析青海地區的應變特征.

1 時間序列噪聲分析方法

目前大部分測繪工作者主要使用時間序列分析軟件CATS和HECToR等軟件對不同區域的GPS觀測數據進行時間序列噪聲分析. 其中，CATS軟件使用最大似然估計法(MLE)且具有較為精確的算法和模型. 但是，在處理時間跨度較大并且噪聲類型較為復雜的時間序列數據時，CATS軟件的處理速度十分緩慢. 為更高效處理含有大量數據的時間序列，BOS等[9]研發了HECToR軟件，該軟件通過算法改進提高了數據處理的速度，很好地克服了CATS軟件的弊端. 改進后的MLE即為貝葉斯信息準則(BIC).

1.1 MLE

目前坐標時間序列分析普遍使用MLE，該方法可以得到GPS坐標時間序列中所涉及到的絕大部分參數. 坐標時間序列表示為

式中：ti為歷元，以a為單位；a為初始位置；b為線性速率；c、d、e、f分別為周期項的系數；H為海維西特階梯函數；gj為同震偏移；vi為殘差.

1.2 BIC

Hector軟件使用BIC來評價擬合結果的優良性，該軟件能夠對時間序列的線性趨勢項、高階多項式、季節項、其他周期項信號以及多種噪聲模型的組合進行估計[10]. 使用BIC分析噪聲模型的公式為

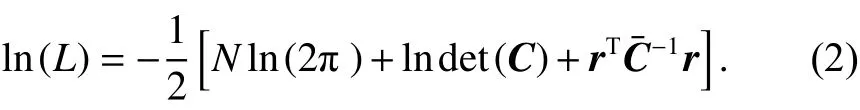
式中：N為實際觀測數，r為殘差矩陣；協方差矩陣C可分解為

其中， σ 為殘差序列的標準差，其計算公式為

detcA=cNdetA

由 可得

于是可得

似然函數L越小，BIC值越小，噪聲模型相對越好；反之，似然函數L越大，BIC值越大，噪聲模型相對越差.

2 時間序列分析

2.1 數據來源

CMONOC是中國地殼運動觀測網的延續，在中國境內共設置了260個連續站，青海境內共有14個連續站，選取GAMIT/GLOBK 軟件解算得到的青海地區2010—2020年的14個CMONOC連續站為基礎數據，測站分布如圖1所示. 本文數據來源于中國地震局GNSS數據產品服務平臺[11].

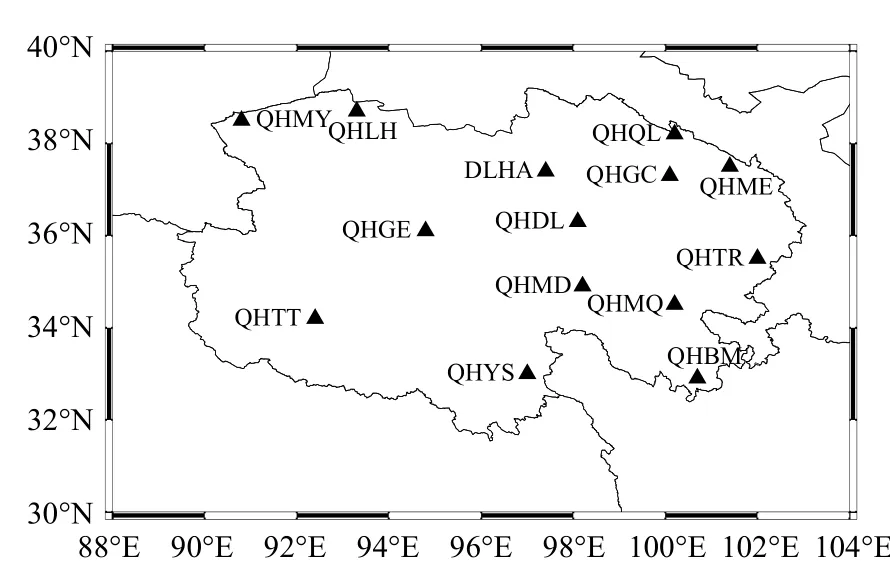
圖1 青海地區CMONOC站點分布圖

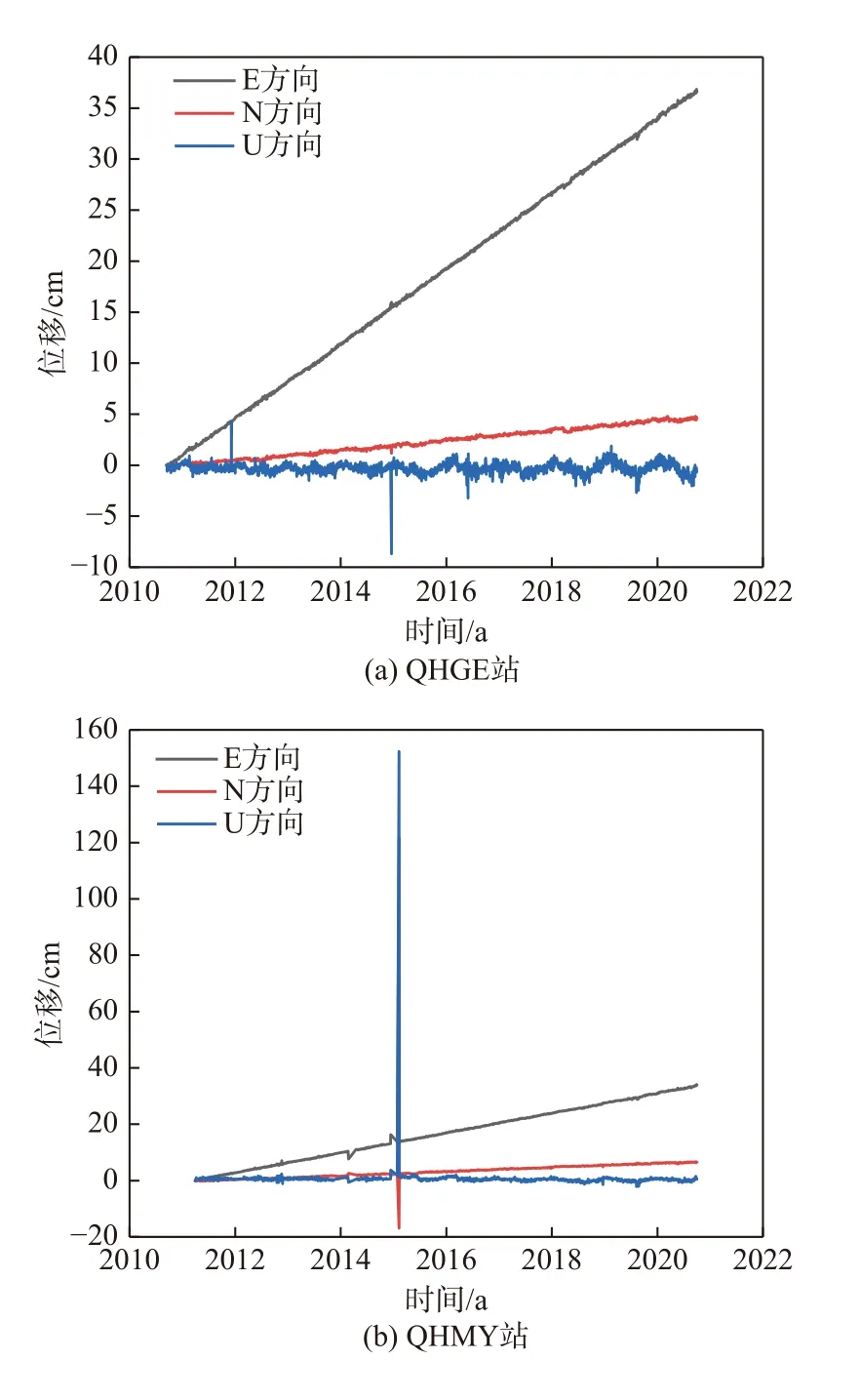
此處僅展示QHGE、QHMY和QHTR站的原始坐標時間序列. 如圖2所示，原始坐標時間序列的東(E)、北(N)、天頂(U)方向都存在異常值，必須予以剔除. E方向表現為線性遞增趨勢，斜率較大；N方向表現為線性趨勢，斜率較小；U方向表現為周期變化趨勢.

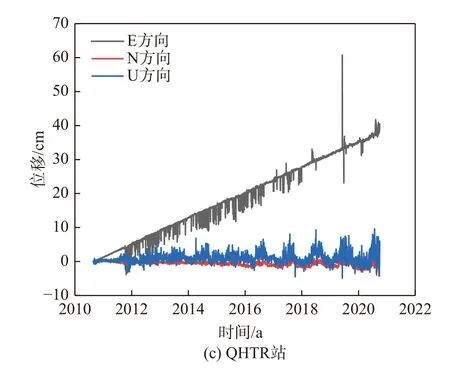
圖2 測站原始時間序列圖

2.2 原始時間序列處理

本文利用最小二乘法估計并剔除坐標時間序列中的線性趨勢和周期性趨勢來計算殘差，并使用四分位數粗差探測方法剔除異常值. 具體步驟包括：1) 采用最小二乘法剔除原始時間序列中的線性趨勢和周期性趨勢，得到時間序列中的殘差；2) 用四分位距探測殘差時間序列包含的異常值，然后剔除；3) 擬合剔除異常值之后的殘差時間序列并重復步驟2)，直到完全剔除[9]. 圖3為處理后的殘差時間序列.

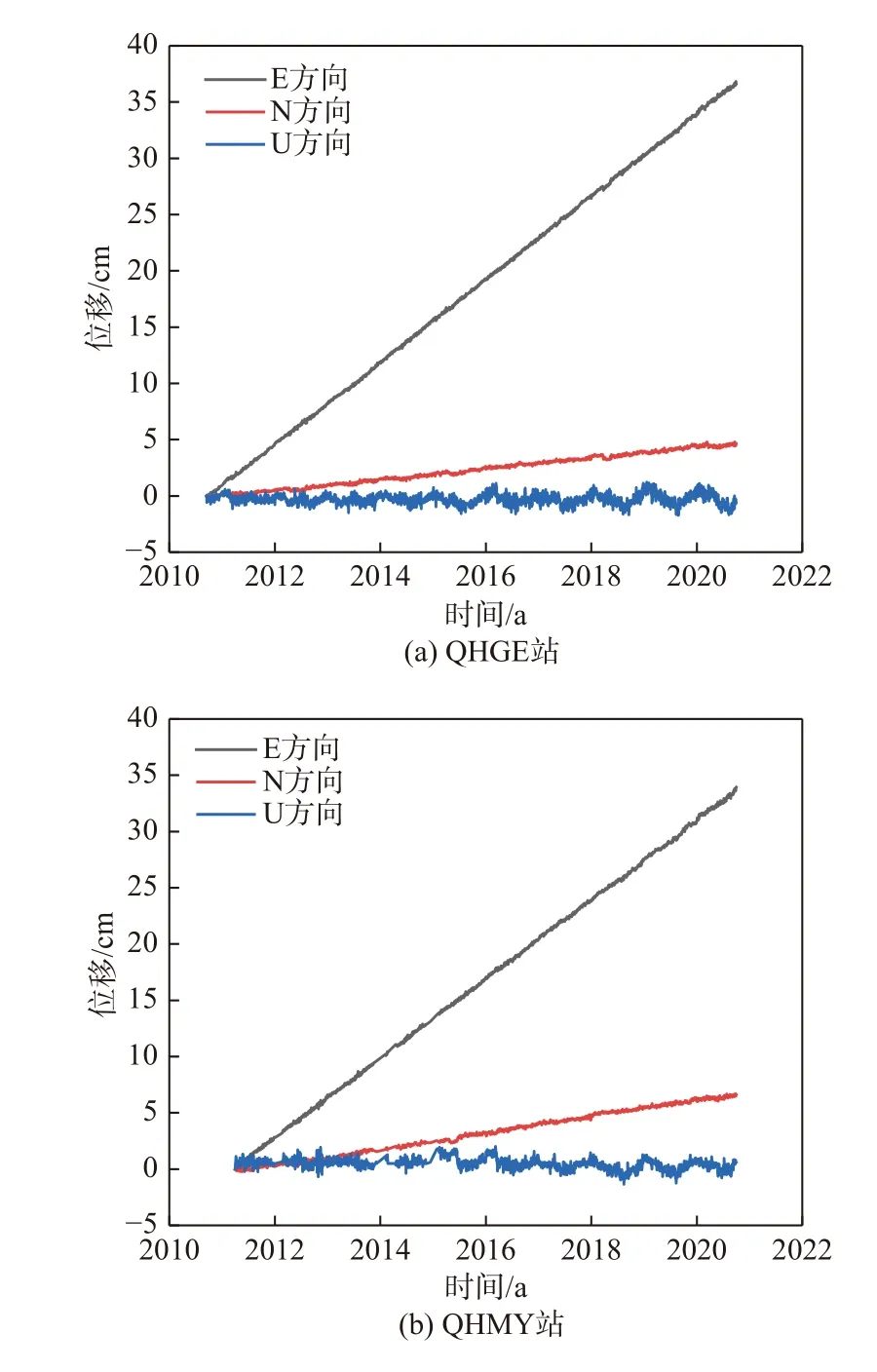
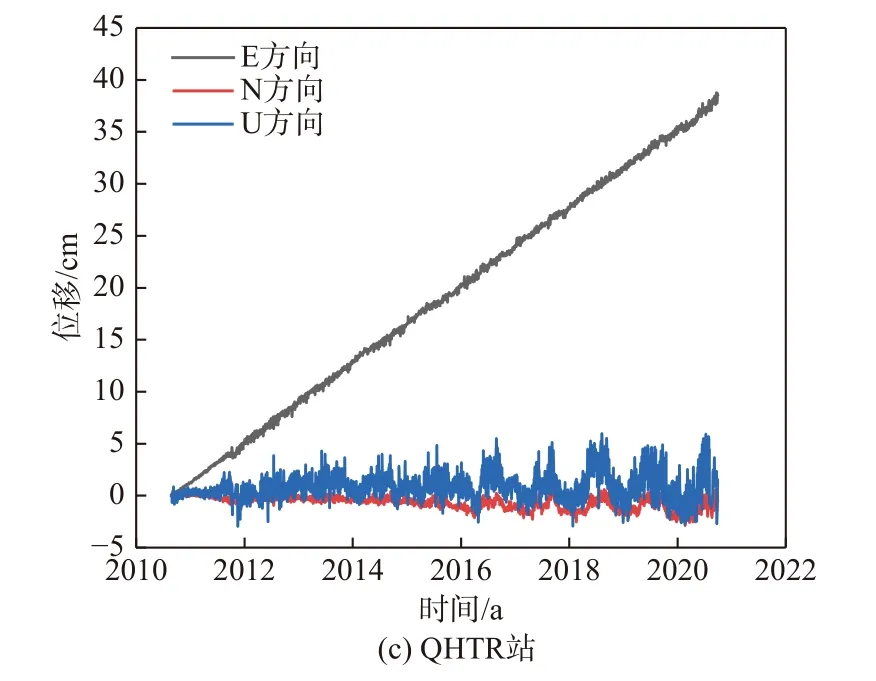
圖3 處理后測站殘差時間序列圖

2.3 最優噪聲模型的確立

對14個CMONOC連續站E、N、U方向的時間序列數據進行解算，并將WN與FN、PL、GGM及FN+RW進行組合，利用這四種組合模型計算每個測站所對應E、N、U方向的BIC值，對比各個模型所得BIC值即可獲得所有站點各方向的最優噪聲模型.表1為各方向噪聲模型所占百分比，由表1可知，各方向具有不同噪聲特征. 在E、N、U方向上，最優噪聲模型分別為 WN+PL、WN+GGM和WN+FN.

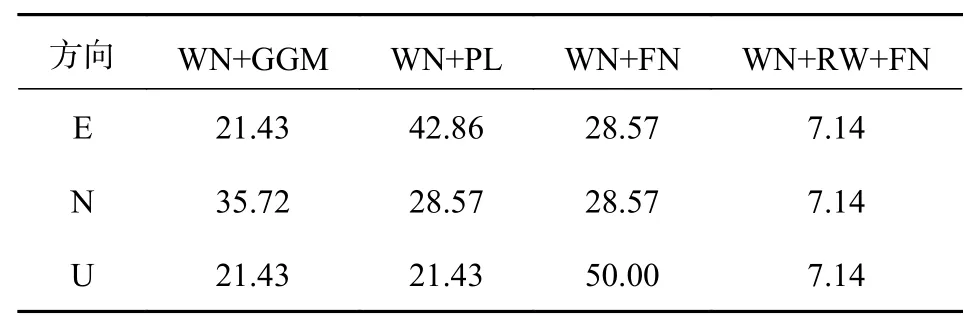
表1 E、N、U方向噪聲模型百分比 %

3 顧及有色噪聲的青海地區水平速度場分析

圖4為青海境內未經最優噪聲模型修正的CMONOC連續站的水平運動速度場. 由圖4可知，青海地區的整體運動方向近E方向，東部地區的運動方向近E方向，其余地區的運動方向為E、N方向.未經最優噪聲模型修正的青海CMONOC連續站在ITRF14框架下水平運動方向為88°55′10″NEE，平均速度為39.58 mm/a. E方向的平均速度為39.57 mm/a，標準差為5.09 mm；N方向的平均速度為0.75 mm/a，標準差為3.76 mm.

圖4 修正前的水平速度場

圖5為經最優噪聲模型改正后的青海CMONOC連續站的水平運動速度場，修正后的青海CMONOC連續站在ITRF14框架下水平運動方向為88°57′58″NEE，平均速率為39.45 mm/a. 并且，E方向的平均速度為39.44 mm/a，標準差為5.01 mm；N方向的平均速度為0.71 mm/a，標準差為3.76 mm. 將最優噪聲模型修正前后的速度場進行對比分析可知，修正后速度場的精度優于修正前速度場的精度，其平均水平運動速率相差0.13 mm/a；水平運動方向相差2′48″NEE.

4 顧及有色噪聲的青海地區應變特征分析

4.1 應變分析模型

以往研究表明，地殼板塊是彈塑性體或黏彈性體，在周圍板塊的作用下會產生整體平移、旋轉和內部形變[12-13]. 塊體內部應變的實質是板塊內部質點的運動，并且這些質點運動的應變參數往往是與位置相關的線性函數[14-15]. 顧及板塊的整體運動與線性形變可得塊體的整體旋轉與線性應變模型，其形式為[16]

式中：A0～A2、B0～B2、C0～C2為板塊的應變參數； ωx、ωy、ωz為板塊的歐拉矢量的3個分量；r為地球半徑；λ為質點的大地經度；φ為質點的大地緯度.

4.2 應變場分析

本文利用經最優噪聲模型改正后的速度場建立青海地區地殼水平運動的整體旋轉與線性應變模型.通過分析計算得到青海地區內部形變的空間分布特征并繪制該區域的主應變圖、面膨脹圖以及最大剪應變圖. 由圖6可知，青海地區東北部表現為明顯的擠壓應變特征，而該地區的西南部主要表現為拉張特征，最大主壓應變和最大主張應變分別出現在青海地區的東北角與西南角，其值分別可達-4.31×10-8和4.56×10-8. 由圖7可知，青海地區的東北、西南部為最大剪應變高值區，對應構造活動較強烈. 面膨脹率反映擠壓與拉張作用的相對大小，正、負值分別表示以張性活動或壓性活動為主. 由圖8可知，從東北向西南，擠壓應變逐漸減小，拉張應變逐漸增大，總體表現為擠壓應變.

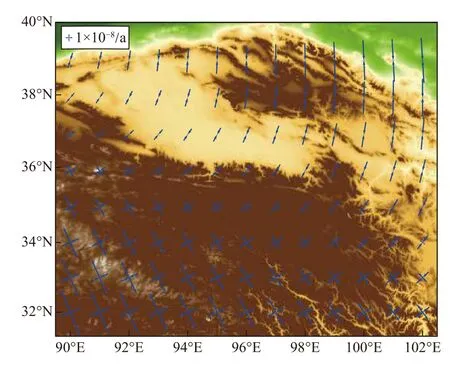
圖6 主應變圖

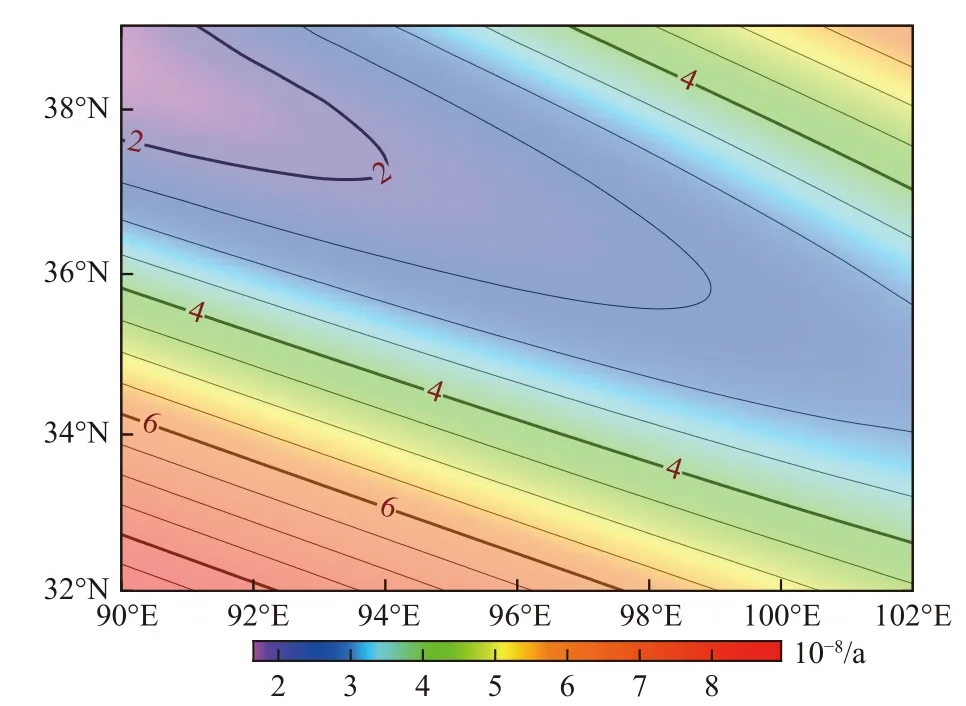
圖7 最大剪應變圖

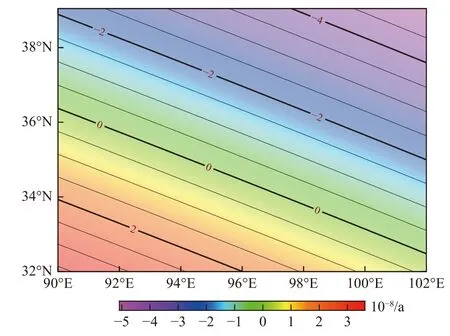
圖8 面膨脹圖

5 結 論

本文基于最優噪聲模型，對青海境內14個CMONOC連續站2010—2020年期間的觀測數據進行分析. 首先，利用最優噪聲模型得到修正后的青海速度場. 其次，使用整體旋轉與線性應變模型對速度場進行插值，并求出應變參數. 最后，根據所得結果對青海地區的應變特征進行分析，結論如下：

1)青海地區CMONOC連續站坐標時間序列在E、N、U方向上具有不同的噪聲特性，其最優噪聲模型分別為組合模型PL+WN、GGM+WN和 FN+WN；

2)考慮CN影響后的速度場精度明顯優于未經修正的速度場精度，修正前后的水平運動方向和平均水平運動速率差值可達2′48″NEE和0.13 mm/a，修正后青海地區CMONOC連續站基于ITRF2014框架下水平方向運動的平均速率為39.45 mm/a，運動方向為88°57′58″NEE；

3)青海地區的東北、西南部構造活動較強烈，東北部表現為明顯的擠壓應變特征，而西南部主要表現為拉張特征. 從東北往西南，擠壓應變逐漸減小，拉張應變逐漸增大，總體表現為擠壓應變.