基于隨機森林的航站樓負荷預測及特征分析

楊勝維 吳利瑞 劉東

同濟大學機械與能源工程學院

航站樓作為典型的公共交通建筑，每平方米耗電量遠遠高于普通公共建筑，其中空調系統運行電耗占比最大，為61%[1]。航站樓空調負荷中新風負荷和人員負荷之和占比為45%～60%[2]，客流量的變化對實際負荷需求的有顯著的影響[3]。而航站樓區域供冷系統水力半徑大，長距離的冷凍水輸送會導致冷源供應側和需求側的延遲較大，傳統反饋調節的控制方式不能反映系統的實時負荷變化[4]。通過準確的負荷預測建立前饋的控制策略是應對這一問題的有效方法。本文針對航站樓空調負荷特點，建立了隨機森林負荷預測模型，并分析了不同的輸入特征選擇對模型預測準確性及效率的影響，為空調設備實際運行調控及優化提供指導依據。

1 隨機森林算法

隨機森林是一種并行式集成學習算法，在以分類回歸決策樹（CART）為基學習器構建 Bagging 集成的基礎上，進一步在決策樹的訓練過程中引入了隨機屬性選擇，由森林中所有決策樹投票得出結果。隨機森林的泛化性能強、簡單易實現、計算開銷小，在很多分類、回歸任務當中具有較高的準確度[5]。

1.1 CART 決策樹

決策樹是 Breiman L 等人于 1984 年提出的一種決策樹學習算法，使用“基尼指數”來選擇劃分屬性。假設數據集D包含m個類別，則其基尼指數GD的計算公式為：

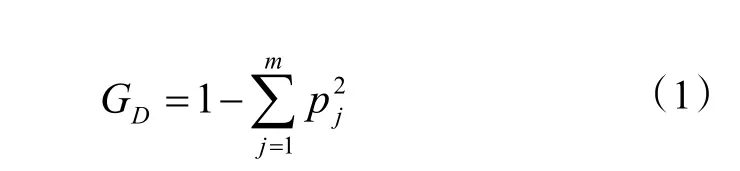
式中：pj為j類元素出現的頻率。

基尼指數反映了從數據集D中隨機抽取兩個樣本，其類別標記不一致的概率，基尼指數越小，數據集D的純度越高。因此，在m個類別中，挑選基尼指數最小的類別作為最優劃分屬性。

1.2 隨機森林算法流程

隨機森林在 CART 決策樹的基礎上引入了Bagging 方法提高基學習器的泛化能力并增強單棵決策樹的性能，同時降低泛化誤差[6]。此外，隨機森林還有袋外估計的特點，不需要額外挑選訓練集。隨機森林的算法流程可分為以下幾步：

1）隨機抽取樣本：通過Bootstrap 重抽樣方法從原始數據樣本中抽取n個樣本作為訓練集，理論上往往會有大約1/3 的原始數據沒有被選中，這部分數據則會作為測試集，評估其泛化誤差。

2）隨機抽取特征：對于每一個Bootstrap 樣本集進行決策樹建模，假設其中有d個特征，則隨機抽取k個特征（k≤d），從k個特征中選擇最佳分割特征作為節點建立CART 決策樹。

3）建立森林：重復以上步驟m次，建立m課CART 決策樹組成隨機森林。

4）對于測試集的樣本，通過森林中所有決策樹的投票結果（對于分類問題）或算術平均值（對于回歸問題）得到最終預測值作為輸出。

2 航站樓負荷預測模型

本文以華東某機場衛星廳為負荷預測對象，通過空調系統實際運行的歷史數據，該機場航站樓總建筑面積約為 62 萬m2，設計總冷負荷為 93577 kW，分為S1 和S2 兩部分。主要功能區包括值機大廳、安檢區、候機區、旅客到達走廊、行李提取大廳、接待大廳等，并根據功能特點設置相應的商業店鋪，以滿足旅客餐飲、購物等需求。航站樓的空調負荷由能源中心的區域供冷系統承擔，空調水系統為三級泵冷水直供系統，從能源中心產生的冷水，經二級泵系統輸送至航站樓內三個熱力站內，再通過設置在熱力站的三級泵輸送至航站樓內各個空調末端。該空調系統間歇運行，每日凌晨2:30～4:30 停止供冷。

2.1 數據預處理

采集的原始數據包括室外干球溫度、室外相對濕度、進出人數、系統總供回水溫度、冷凍水流量。各項數據的時間范圍為7 月1 日至10 月1 日，涵蓋整個制冷季節，時間間隔為 30 min，原始數據集共包含 4416組數據樣本。由于數據傳感器故障或干擾信號等因素，原始數據集中存在數據缺失、數據異常、數據波動等現象。這些異常數據的存在會使機器學習模型的性能降低，因此數據預處理是必不可少的一步。通過數據清洗、缺失值補充、離群點剔除等手段，可以提高數據的質量、提升模型的準確性、縮短計算過程。

缺失值處理：對于室外溫濕度的缺失值，則根據Wunder Ground 全球氣象數據庫中當地對應時刻的室外溫濕度數據進行補全。對于進出人數、系統總供回水溫度、冷凍水流量等參數的缺失值，采用插值補全，用相鄰時間點的數據平均值代替。

離群點處理：由系統總供回水溫度與冷凍水流量計算可以得到各個時刻對應的冷負荷，冷負荷的概率分布圖如圖1 所示，可以看到冷負荷服從正態分布。通過判斷冷負荷數據是否滿足拉依達準則（3σ準則）來剔除離群點：冷負荷數據落在（μ- 3σ,μ+3σ）區間之外的被認為是異常數據，將剔除該冷負荷對應時間點的數據。其中冷負荷在0 MW～5 MW 區間概率分布較高是因為空調系統間歇運行導致，因此拉依達準則對于低負荷離群點的剔除較為局限，需要結合間歇運行的時間判斷低負荷數值是否為離群點：若低負荷數值出現在凌晨2:30～4:30 則認為是正常數據，反之則作為異常數據剔除。

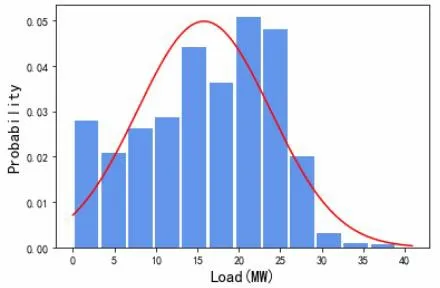
圖1 冷負荷分布圖

噪聲處理：即使對應的冷負荷落在置信區間內，對于進出人數、室外溫濕度等數據，仍然不可避免地存在數據噪聲，如圖2 所示為每日進出累計人數，這是由傳感器高頻測量的物理變量的隨機誤差導致的。因此，為了降低噪聲干擾，需要對曲線進行濾波，讓曲線過渡更平滑。本文采用 Savitzky-Golay 濾波器對數據進行平滑處理，其核心思想：是對一定長度窗口內的數據點進行k階多項式擬合，從而得到擬合后的結果。這種濾波器的最大特點：在濾除噪聲的同時可以確保信號的形狀、寬度不變。平滑處理后得到的每日進出累計人數的曲線如圖3 所示。

圖2 去噪前每日進出累計人數

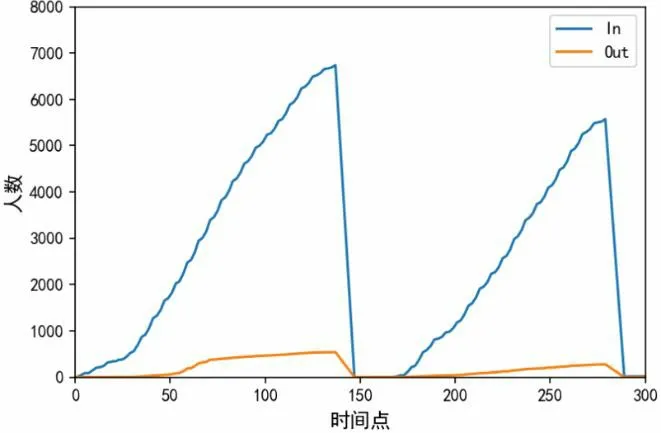
圖3 去噪后每日進出累計人數

2.2 特征工程

正確構建的特征可以在不犧牲預測精度的情況下減少數據驅動模型的計算時間[7]，對于航站樓空調負荷預測，本文挑選了室外干球溫度，室外相對濕度，進出人數，時間及歷史負荷作為原始特征，并進一步處理得到更能反映航站樓空調負荷變化規律的輸入特征。

2.2.1 時間特征

原始數據中時間的數據是以日期的格式儲存的，如2020 年7 月1 日12:00:00。在目前研究的負荷預測模型中，一般將其轉化為時間戳格式或 24 h 格式。前者代表了從1970 年 1 月1 日00:00:00（UTC/GMT 的午夜）開始到當前時間所經過的秒數，后者則是日期格式中對應的小時數。因此，時間戳格式表示的時間數據是單調遞增的，而24 h 格式表示的時間數據是以24為周期的鋸齒狀周期函數。而航站樓的空調負荷存在明顯的24 h 特征與星期特征，如圖 4 和圖5 所示。

圖4 顯示了 2020 年 7 月 30 日 00:00:00～2020 年8 月 1 日 00:00:00 航站樓的 48 h 內每 30 min 的冷負荷變化，可以看到冷負荷表現出明顯的 24 h 特征。由于空調系統間歇運行，在每日系統重新開始運行的 1 h內，系統需要處理停機期間的蓄熱，此時的冷負荷達到峰值。圖5 顯示了2020 年8 月3 日～2020 年 8 月 16日航站樓的日負荷變化情況，在兩周內室外平均溫度基本穩定在30 ℃左右的條件下，冷負荷表現出明顯的星期特征。整體趨勢為一周內冷負荷隨星期數上升，在星期五達到峰值后回落。

圖4 冷負荷24 h 特征

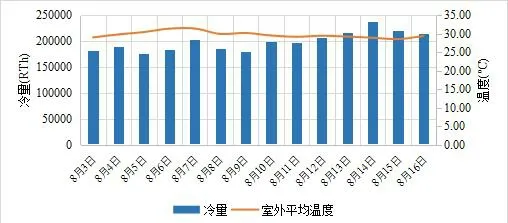
圖5 冷負荷星期特征

通過上述分析，將時間拆分為 24 h 特征和星期特征更能反映冷負荷的變化規律。因此，通過式（2）和式（3）將數據樣本的時間轉化為兩組特征。

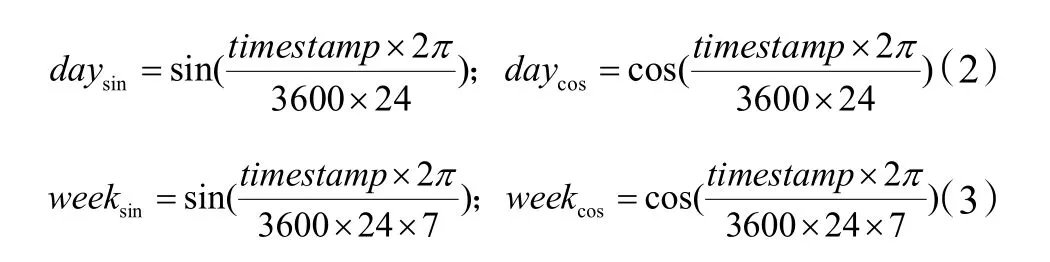
式中：timestamp為數據樣本對應的時間戳。

2.2.2 客流特征

人員數量是影響航站樓實際負荷需求的重要因素，航站樓人員密度實際運行階段的真實值顯著低于設計值，導致空調系統新風負荷與人員負荷供需不匹配[8]。目前對于航站樓客流特征常用的數據一般是主要出入口的客流量——進出人數隨時間的變化，而某一時刻的客流量并不能直接反映航站樓內對應的人員數量。因此，本文擬通過式（4）計算某一時刻航站樓內的逗留的人員數量。

式中：Nt為t時刻航站樓內逗留的人員數量；At為t時刻進入航站樓的人數；Bt為t時刻離開航站樓的人數；Ct為t時刻從該機場飛離的人數；Dt為t時刻降落到該機場的人數。

圖6 為航站樓內逗留人員數量示意圖。其中，At和Ct可以通過航站樓主要出入口的客流統計攝像頭得到，而Bt和Dt則與航班動態相關，較難直接獲取相關數據。但后兩者與前兩者存在時間上的關聯，從該機場飛離的人在先前的時間會被入口客流統計捕捉到，而降落到該機場的人則在后續的時間會被出口客流統計捕捉到。同時，將迎接旅客和送別旅客的人群考慮在內，可以將式（4）改寫為式（5）。

圖6 航站樓內逗留人員數量示意圖

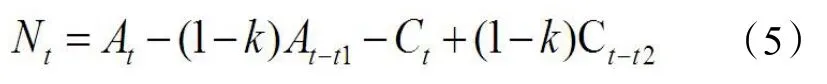
式中：k為迎送比，國內迎送比 0.3，國際迎送比 0.5[9]，取平均值0.4；t1 為出發過程停留時間；t2 為到達過程停留時間。

Liu 等人[10]的研究表明：乘客在航站樓出發過程中花費的時間較長，而到達過程往往很快，通過現場調研得到的平均停留時間分別為132 分鐘和34 分鐘。因此，結合數據集的時間步長，t1 和t2 分別取 120 min和30 min。通過式5 計算得到的航站樓人員數量部分曲線如圖7 所示。可以看到，航站樓的逗留人員數量在每日8:00 和16:00 兩個時刻達到峰值，這與上下班高峰期的時間吻合。

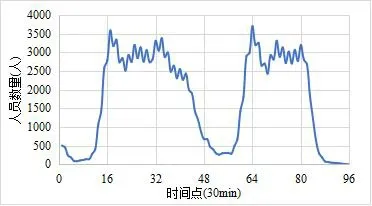
圖7 航站樓內逗留人員數量曲線

2.2.3 氣象特征

室外溫濕度數據反映了室外空氣的狀態點，而室外空氣焓值代表了空調系統將新風處理到送風狀態需要提供的冷量。因此，在室內要求的溫濕度不變的條件下，室外空氣的焓值更能反映空調冷負荷的變化規律。已知室外溫濕度數據，可通過式（6）計算對應焓值h。

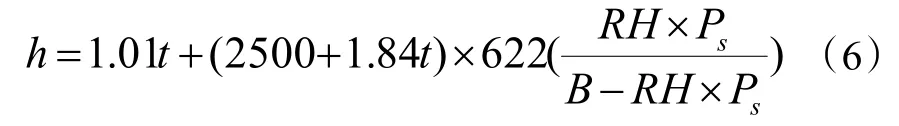
式中：t為室外干球溫度，℃ ；RH為室外相對濕度，% ；Ps為水蒸氣飽和分壓力，可 查水蒸氣表，和 溫度一一對應，P a；B為大氣壓，取 101325 Pa。

2.3 模型訓練及參數尋優

綜合上述分析，將時間 24 h 特征、時間星期特征、人員數量、室外干球溫度、室外相對濕度、室外空氣焓值、歷史負荷作為隨機森林算法的輸入特征進行模型訓練。在采用隨機森林進行回歸任務時，需要對模型參數進行定義，主要參數包括：決策樹的數量（n_estimators）、樹的最大生長深度（max_depth）、葉子的最小樣本數量（min_samples_leaf）、分支節點的最小樣本數量（min_samples_split）。對隨機森林模型來說，樹越茂盛，深度越深，枝葉越多，模型就越復雜。模型過于復雜會導致過擬合且計算效率低，而過于簡單則會導致欠擬合且預測精度低，兩者都會讓泛化誤差高。因此需要尋找最優的參數組合建立模型，目前常用的參數優化方法包括網格搜索法和隨機搜索法。

其中網格搜索法是指定參數值的一種窮舉搜索方法，遍歷所有的參數組合通過交叉驗證的方法進行優化來得到最優的學習算法。但對于隨機森林算法來說，需要調整的參數很多，如果采用網格搜索法則需要大量的搜索時間。而隨機搜索法對于多參數的機器學習算法適用性更強[11]，這種方法通過在給定參數范圍內隨機選擇參數值進行指定次數的參數組合，然后找出泛化誤差最小的一組參數組合。因此，本文采用隨機搜索法對隨機森林模型進行參數調優，并以最優參數組合進行模型訓練。

2.4 模型評價

對于模型的預測性能，根據 ASHRAE 指南14-2014[12]選取了三個指標評估預測結果的準確性：歸一化平均絕對誤差（NMAE）、累積均方根誤差（CVRMSE）以及擬合優度(R2)，各項指標的計算公式見式（7）～（9）。

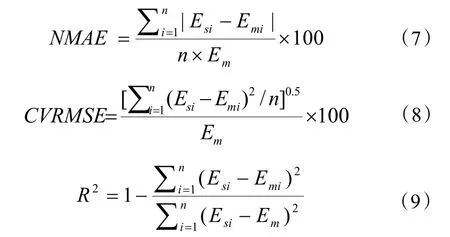
式中：Esi為第i組數據的預測冷負荷，k W；Emi為第i組數據的實際冷負荷，kW；Em為實際冷負荷平均值，kW；n為數據樣本數量。

ASHRAE 指南 14-2014 中指出，在使用小時負荷預測值時，負荷預測模型的NMAE 和CVRMSE 應分別保證小于 10%和 30%，此時模型預測的結果是可接受的。

3 模型性能對比及特征分析

為分析不同輸入特征組合對負荷預測模型性能的影響，建立了五組模型，其中時間特征均包括24 h特征與星期特征。對于歷史負荷，考慮到模型的可用性，時間窗口不宜選擇過長，故每組模型的歷史負荷時間窗口取值范圍為1～4，即采用前1～4 個時刻對應的負荷數據作為歷史負荷特征。每組模型挑選出預測性能表現最好的模型進行對比，各組模型性能對比如表1 所示，各組模型參數及訓練時間如表2 所示，冷負荷預測準確度的情況如圖 8 所示，其中黑色虛線為10%誤差線。

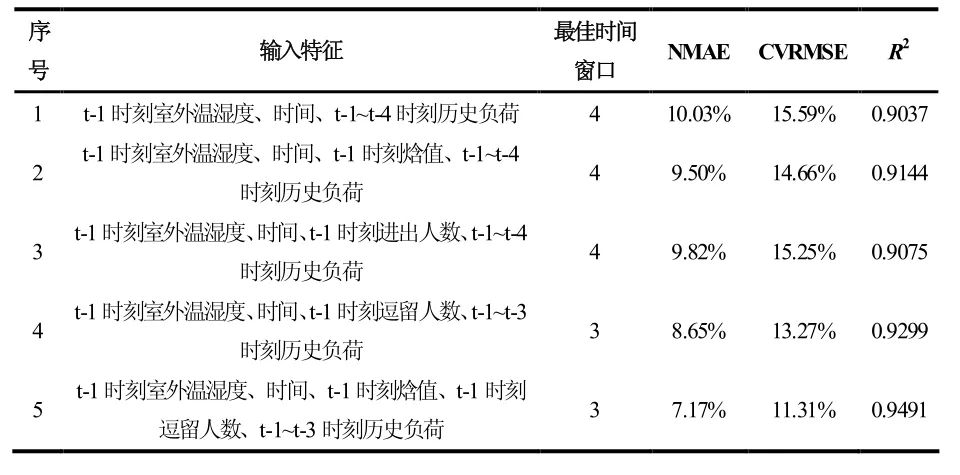
表1 各組模型性能對比情況

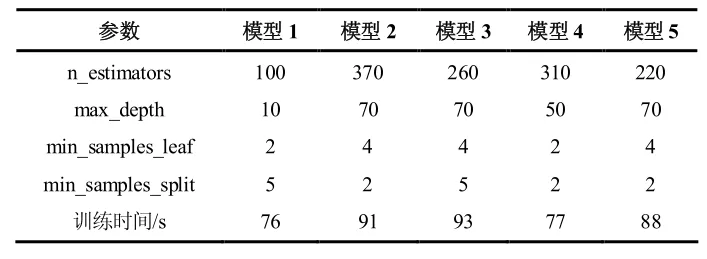
表2 各組模型參數及訓練時間

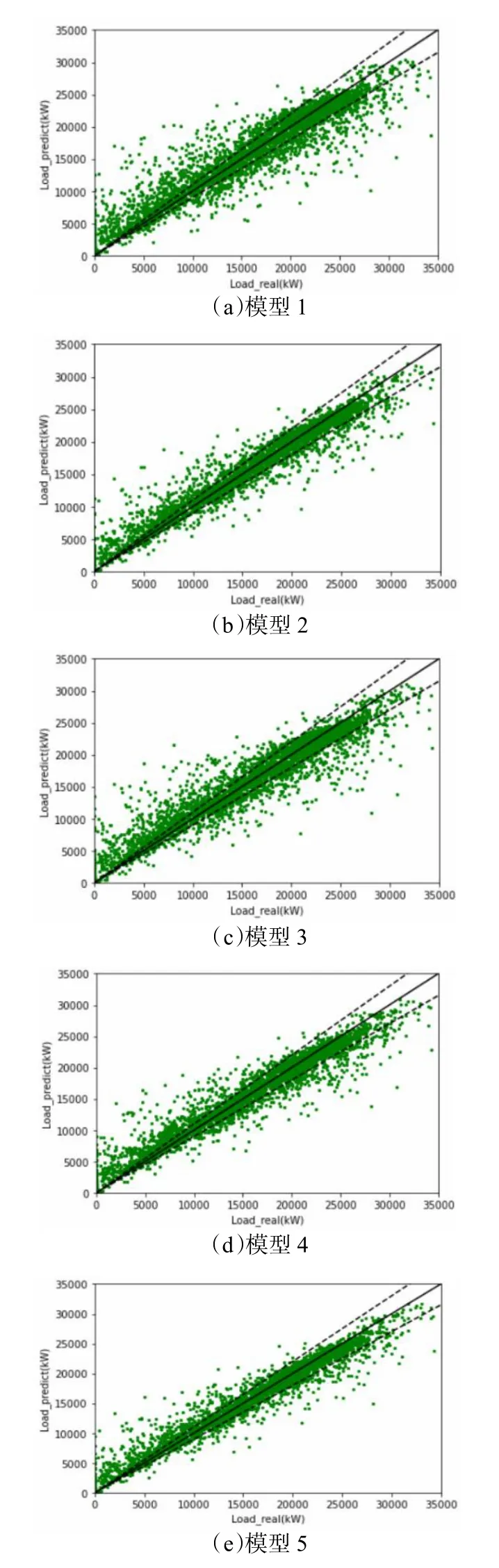
圖8 冷負荷預測值與實際值對比圖

表 1 和表 2 顯示：除模型 1 外，其余模型均能滿足ASHRAE 指南14-2014 要求的性能，且五組模型的訓練時間均不超過100 s。由表1 的模型2 與模型4 可以看出，在室外溫濕度、時間、歷史負荷的基礎上，增加焓值或逗留人數作為輸入特征均可以提升航站樓負荷預測模型的性能。在模型 3 中，增加原始客流特征——進出人數作為輸入特征并不能提升模型性能，這說明進出人數與冷負荷的相關性較弱，不能準確反映冷負荷的變化規律。在正確選擇輸入特征的條件下，隨著輸入特征維度的增加，隨機森林模型的復雜度反而下降，歷史負荷的最佳時間窗口相應下降，且由表2 可知，模型訓練的效率也相應提高。

圖8 顯示了不同模型的預測準確度，各個模型在低負荷區域（0 kW～10000 kW）的準確度較差，這是由于間歇運行系統停機時間存在人為操作的隨機性導致的。隨著輸入特征被正確選取，預測值與實際值的誤差逐漸減小。模型5 在15000 kW～35000 kW 負荷范圍的預測誤差基本控制在10%以內。對模型5 進一步分析，各個輸入特征的貢獻度如圖9 所示。

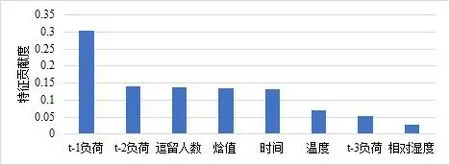
圖9 模型5 輸入特征貢獻度

由圖 9 可知：負荷預測模型各個輸入特征中對預測結果貢獻最大的特征是歷史負荷，尤其是前 1 h 內的負荷數據，而時間間隔超過1 h 的負荷數據對預測結果的貢獻較小。需要注意的是：客流特征對于負荷預測的相關性僅次于歷史負荷，甚至高于常用的室外溫濕度特征，這說明航站樓等公共交通建筑中客流特征對于負荷變化有顯著的影響。此外，氣象特征、時間特征對于負荷預測的貢獻相當，氣象特征中焓值的貢獻度遠高于溫濕度。這說明相比于溫濕度，室外空氣焓值是對負荷預測更有效的氣象特征。

4 結論

本文基于隨機森林建立負荷預測模型，結合航站樓空調負荷特點，對模型輸入特征進一步拆分細化，引入客流特征、室外空氣焓值、時間 24 h 及星期特征作為輸入特征，利用實際運行數據進行訓練，并對不同特征組合進行分析研究，得到以下結論：

1）對于航站樓空調負荷，各輸入特征對預測結果的貢獻度大小排序依次為：前 30 min 負荷>前 1 h 負荷 >逗留人數 >室外空氣焓值 >時間 >室外干球溫度>前1.5 h 負荷>室外相對濕度。

2）對于輸入特征的選擇，客流特征是航站樓等公共交通建筑空調負荷的重要影響因素，逗留人數相比于進出人數更能反映負荷的變化規律；前 1 h 內的歷史負荷對負荷預測的相關性較高，超過 1 h 的歷史負荷對預測結果的貢獻較小；室外空氣焓值對于空調負荷預測結果的影響比室外溫濕度更加顯著。

3）隨機森林算法在航站樓負荷預測方面對多維度輸入特征的適用性較強，在正確選擇相關性較高的輸入特征的前提下，隨著輸入特征維度增加，模型的復雜度訓練效率更高，預測性能更好。