深度神經網絡模型構建及優化策略

楊波，梁偉

摘? 要： 針對深度學習構建網絡模型以及確定模型參數的問題，在分析神經網絡基本結構和線性模型局限性的基礎上，研究了深度神經網絡設計的關鍵因素和優化策略。結合手寫數字識別問題，對優化策略、動態衰減學習率、隱藏層節點數、隱藏層數等情形下的識別正確率進行了實驗。結果表明，不同神經網絡模型對最終正確率有質的影響，相同優化策略在不同參數取值時對最終正確率有很大影響，并進一步探究了具體選取優化策略和參數的方法。

關鍵詞： 人工智能; 深度學習; 神經網絡; 手寫數字識別; MNIST數據集

中圖分類號：TP391? ? ? ? ? 文獻標識碼：A? ? ?文章編號：1006-8228（2022）01-08-06

Model construction and optimization strategies of deep neural networks

Yang Bo1， Liang Wei2

（1. Chenzhou Vocational and Technical College， Chenzhou， Hunan 423000， China; 2. College of Infomation Science and Engineering， Hunan University）

Abstract： Aiming at the issues of building the network model and determining the model parameters in deep learning， on the basis of analyzing the basic structure of neural networks and the limitations of the linear model， the key factors and optimization strategies of designing deep learning neural networks are studied. Combined with the handwritten numeral recognition problem， a large number of experiments are carried out on the recognition accuracy under the conditions of optimization strategy， dynamic attenuation learning rate， number of hidden layer nodes and number of hidden layers. The results show that different neural network models have a qualitative impact on the final accuracy rate， and the same optimization strategy has a great impact on the final accuracy rate when different parameters are selected. Furthermore， the specific selection method of optimization strategy and parameters is explored.

Key words： artificial intelligence; deep learning; neural networks; handwritten digit recognition; MNIST data set

1 神經網絡模型

最早的神經網絡數學模型是由W. S. McCulloch和W. Pitts提出[1]，其MCP模型仿效了人類神經元的工作機理。該模型需要手動設置權重，即麻煩又難以得到最優結果。為了讓計算機自動且合理地設置權重，F. Rosenblatt提出了感知機模型[2]，該模型可根據樣例數據學習特征權重。F. Rosenblatt在文獻[3]中深入闡釋了感知機理論及背景。感知機模型可以簡單地理解為后續提到的單層神經網絡。

1.1 神經元

神經網絡的最小構成單元是神經元。神經元通常有多個輸入和一個輸出，其輸出就是該神經元的所有輸入經過某種運算后得到的結果。最簡單的輸出就是對輸入進行加權和，如圖1所示。

1.2 神經網絡的結構

神經元之間的連接結構，構成神經網絡結構。如果相鄰兩層的神經元都有連接則稱為全連接神經網絡，如圖2所示。

每個輸入層節點有一個輸入值，該值也通常看作是該輸入節點的輸出值。機器學習中，神經網絡輸入層所有節點通常對應特征向量，輸入層每個節點的值對應特征向量的每個分量值。對于隱藏層，每個節點的輸出值是由該節點的所有輸入值及其對應邊的權重值經過運算得到。當獲得所有隱藏層節點的輸出值，通過運算便可獲得輸出層節點的輸出值。

1.3 神經網絡的數學表示

根據輸入層節點的輸入值，各層節點經過某種運算，便可得出輸出層節點的輸出值，該運算過程稱為神經網絡的前向傳播算法。例如圖2所示神經網絡使用加權運算的前向傳播算法，可用矩陣運算描述：

[X=[x1x2x3]? ? ? W1=w111? w112? w113? w114w121? w122? w123? w124w131? w132? w133? w134]

[W2=w211? w212w221? w222w231? w232w241? w242? ? Y=XW1W2=y1y2]

1.4 神經網絡的訓練

當神經網絡根據輸入值運算后得到輸出值，也就相當于得到了一個推算結果。例如，輸入一張手寫的數字圖片（假如圖片上所寫數字為5），經過神經網絡計算后便會得到一個推算出來的數字（該推算值可能為5也可能不為5）。對于推算結果是否和真實情況一致，取決于多個因素，如連接結構、連接邊的權重參數以及節點運算方式等。

為了提高神經網絡推算結果的正確率，需要不斷調整連接邊的權重參數，每調整一次便要運算一次進行結果驗證。通常，需要進行大量的數據驗證才能將神經網絡調整到最佳狀態，以便神經網絡在遇到未知答案的樣本時能推測出正確結果。顯然，由人工訓練神經網絡是不現實的。R. J. Williams，D. E. Rumelhart以及G. E. Hinton提出了反向傳播算法[4]，能自動訓練神經網絡并大幅降低神經網絡訓練時間。

2 深度神經網絡的設計與優化

2.1 神經網絡的設計

圖2所示神經網絡中，輸出是輸入的加權和，根據矩陣運算的性質可進行如下變換：

[Y=XW1W2=XW1W2=XW']

[= ][i=13xiw'i1i=13xiw'i2=y1y2]

于是，每一輸出節點的輸出值[yj]與輸入節點的輸入[X=[x1x2… xn]]可寫成如下運算形式：

[yj=i=1nxiw'ij]

可以看到，輸出與輸入之間是線性的，稱為線性模型。線性模型能解決的問題有限，只能解決線性可分問題，不能解決復雜問題。深度學習主要研究的是非線性可分復雜問題。

如果使用一個非線性函數對加權和再進行運算，神經網絡就不再是線性模型了。這種非線性函數通常稱作激活函數，常用的有[ReLU]函數、[tanh]函數和[sigmoid]函數等。非線性模型節點結構如圖3所示，其中[b]為偏置項，通常為常數。

如圖3中加入了激活函數的神經元節點可以看成是沒有隱藏層且只有一個輸出的神經網絡，M. Minsky， S. A. Papert指出這種沒有隱藏層的神經網絡不能解決抑或問題[5]。

非線性神經網絡模型中，加入隱藏層，模型相當于具有了組合特征提取功能，更適用于解決不易提取特征向量的問題。因此，設計神經網絡時，需要考慮使用激活函數和隱藏層。

2.2 神經網絡的優化

⑴ 優化目標：損失函數

神經網絡通過前向傳播算法計算得到預測值，將預測值和真實值進行比對得出二者差距值，這種差距值表示的是推算值與真實值之間的損失，越小越好。為評判損失大小，需要定義函數定量地刻畫對應的損失值，即損失函數。

對于分類問題，交叉熵是分類問題常用的一種損失函數。

對于給定的兩個概率分布[p（x）]和[q（x）]，通過[q（x）]來表示[p（x）]的交叉熵定義如下：

[Hpx，qx=-xpxlog （q（x））]

其中，在事件總數有限的情況下，概率分布[p（x）]滿足如下條件：

[?xpx∈0，1andxpx=1]

交叉熵描述的是兩個概率分布之間的距離，而分類問題的神經網絡輸出不一定是概率分布。為了將神經網絡輸出轉變成概率分布，常用方法是在神經網絡的輸出層后額外增加一[Softmax]層，使用[Softmax]處理神經網絡前向傳播得到的結果，將結果轉變一個概率分布。原始神經網絡的輸出[yii=1，2，…，n]經[Softmax]處理后的結果如下：

[y'i=Softmaxyi=eyij=1neyj]

交叉熵用作神經網絡損失函數時，[p]代表的是正確結果的概率分布，[q]代表的是預測結果的概率分布，因此，交叉熵表示的就是使用預測結果概率分布[q]來表達正確結果概率分布[p]的困難程度，很明顯，交叉熵越小，兩個概率分布越接近。

回歸問題解決的是對具體數值的預測，與分類問題不同。回歸問題的神經網絡一般只有一個輸出節點，輸出值就是預測值。回歸問題常用的損失函數是均方誤差[MSE]，定義如下：

[MSEyi，y'i=1ni=1n（yi-y'i）2]

其中，[yi]為一個[batch]（即一小部分訓練數據）中的第[i]個數據的正確答案，[y'i]為神經網絡的預測值。

當然，也可根據問題自定義損失函數，注意的是損失函數定義的是推算值與真實值之間的損失。

⑵ 動態衰減學習率

反向傳播算法中，根據損失函數計算得到預測值與正確值之間的損失大小，以此確定參數調整的下降梯度，再根據下降梯度和學習率更新參數值[4]。在海量訓練數據情況下，每一次訓練如果都計算所有訓練數據的損失函數，非常耗時。為加速訓練過程，減少網絡模型收斂所需要的迭代次數，在實際應用中一般采用計算一個[batch]的損失函數。

學習率代表的是參數更新的幅度，控制參數更新的速度。若學習率過大，更新幅度也大，可能會導致參數在極優值兩側來回移動。學習率越小，越能保證收斂性，但會大大降低優化速度，需要更多迭代輪數。為了解決學習率設定問題，通常采用一種靈活的設置方法--指數衰減法，即在訓練初期使用一個較大的學習率來快速得到一個較優參數，隨著訓練增多，逐步按指數減小學習率，使得模型在訓練后期更加穩定地收斂。常用的指數衰減學習率更新公式如下：

[learningRatenew=learningRatebase*decayRatetrainingStep（now）trainingSteps（decay）]

其中，[learningRatenew]表示更新的學習率，[learningRatebase]表示事先設定的基礎學習率，[decayRate]表示學習率的衰減率，[trainingSteps（decay）]表示學習率衰減一次需要的訓練輪數，也即完整地使用一遍訓練數據需要的訓練輪數，它的值等于總訓練數據量除以一個[batch]的訓練數據量（因為每次訓練只訓練一個[batch]的數據量），[trainingStep（now）]表示當前的訓練輪數。

⑶ 避免過擬合

對于一個含有[n]個未知數和[n]個等式的方程組，當方程不沖突時，可以對未知數求解。在神經網絡中，當訓練數據的總數少于網絡模型的參數時，只要訓練數據不沖突，神經網絡可以很好地記憶住每一個訓練數據的結果而使得損失函數為[0]，這樣會造成神經網絡弱化了訓練數據中的通用特征和趨勢，當使用該神經網絡來推算或預測新的未知問題時，則可能會造成推測失誤。換句話說，當神經網絡模型過于復雜后，它就可以很好的“記憶”每一個訓練數據的隨機噪音而忽略去“學習”訓練數據的通用特征，造成對訓練數據的過擬合。通常使用正則化來實現避免過擬合。正則化的思想就是在損失函數中加入能夠刻畫模型復雜程序的指標。一般來說，當網絡結構確定后，模型的復雜度就只由權重參數決定（偏置項[b]為常數，不影響模型復雜度）。常用的刻畫模型復雜度的正則化函數是[L2]正則化，公式如下：

[R（W）iw2i]

[L2]正則化，是通過限制權重參數大小使得模型不能任意擬合訓練數據中的隨機噪音，并避免參數變得更稀疏，即避免有更多的參數變為[0]。

⑷ 提高健壯性

訓練神經網絡時，為了使網絡模型在測試數據上更加健壯，通常可以對參數采用滑動平均模型。滑動平均模型中，網絡前向傳播計算時，不是直接使用權重參數的值參與計算，而是使用參數的滑動平均值參與計算。為實現滑動平均模型，每個參數需要維護一個影子參數，在每次更新參數時，引子參數的值也會更新，更新公式如下：

[Pshadow=decay*Pshadow+1-decay*P]

[Pshadow]表示影子參數，[decay]表示影子參數的衰減率，[P]為待更新的參數。[decay]決定了模型更新的速度，其值越大模型越穩定，通常設成非常接近[1]。為了使訓練過程前期影子參數更新更快，還可以動態更新[decay]的大小，公式如下：

[decay=mindecay， 1+trainingStep10+trainingStep]

其中，[trainingStep]表示當前的訓練輪數。

根據上述分析，神經網絡的設計目標是要能解決非線性可分的復雜問題，需要使用隱藏層和使用激活函數。神經網絡的優化目標是通過降低損失函數的值（即損失值）來優化網絡參數，最終提高網絡對未知問題的正確預測。實際中，通常是在反向傳播算法中使用指數衰減學習率、給損失函數加上正則化、在前向傳播階段使用滑動平均模型等策略實現對神經網絡進行優化。

3 深度神經網絡應用--以手寫數字識別為例

手寫數字識別是多年研究熱點，研究人員提出了很多方法[6-13]，具有較好的識別正確率。

3.1 數據集介紹

MNIST是一個通用的手寫體數字識別數據集，在Yann LeCun的網站對數據集的訓練數據、測試數據、驗證數據、圖片內容及像素大小均進行了詳細介紹[14]。實驗采用的深度學習工具是TensorFlow，TensorFlow對MNIST數據集做了封裝，能方便加載該數據集。

3.2 神經網絡模型設計

為處理方便，將MNIST數據集中每張圖片的像素矩陣（大小為28*28）放到一個長度為784（784=28*28）的一維數組中，作為神經網絡輸入層的特征向量。因此，神經網絡輸入層設計為784個節點，輸出層設計為10個節點，每個輸出節點對應數字0～9中的一個，輸出節點的輸出值代表的是推測為該節點所對應數字的概率，值最大的輸出節點所對應的數字就是一次推測的結果。在輸入層和輸出層之間，設計一層隱藏層，隱藏層節點數量為500。

網絡設計為全連接網絡，節點采用加權和運算并使用激活函數[ReLU]對運算進行去線性化，在模型中使用了指數衰減學習率、加入正則化的損失函數、滑動平均模型等優化策略。為方便描述，本文中將采用了以上設計和優化策略的神經網絡模型稱為全優化模型。

3.3 參數設置

初始情況下，全優化模型的各策略所需的參數設置如表1所示。實驗開發和運行軟硬件平臺環境如表2所示。

3.4 實驗結果分析

神經網絡關注的目標是訓練后的模型對未知數據的預測正確率，因此實驗中模型的正確率是根據測試集數據計算得到的，而測試集在訓練過程中設置為對模型不可見，以保證模型對未知數據的預判能力。

⑴ 全優化模型與少一項優化策略模型的對比

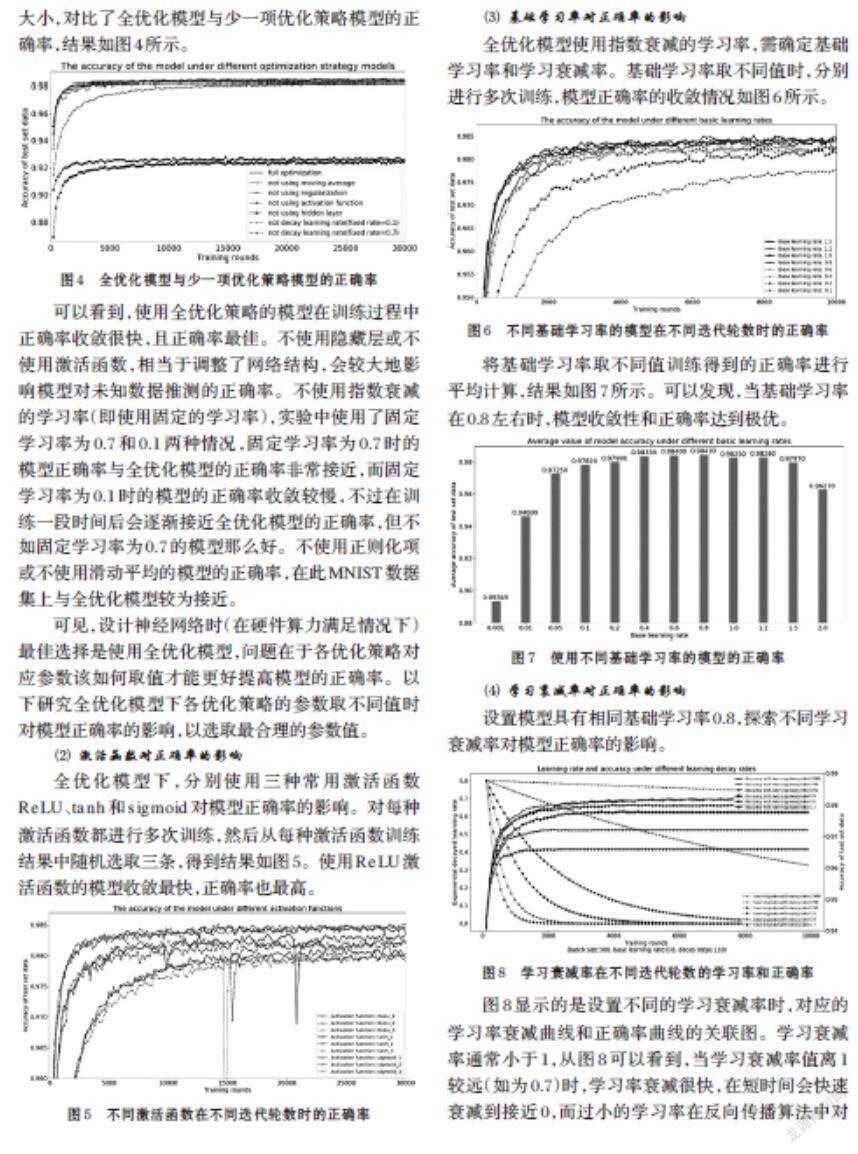
本文所稱的全優化模型概念在上述已描述，少一項優化策略模型是指與全優化模型相比，少了一項優化策略，如少正則化策略的模型、少滑動平均策略的模型等。為探索各優化策略對整體優化效果的影響大小，對比了全優化模型與少一項優化策略模型的正確率，結果如圖4所示。

可以看到，使用全優化策略的模型在訓練過程中正確率收斂很快，且正確率最佳。不使用隱藏層或不使用激活函數，相當于調整了網絡結構，會較大地影響模型對未知數據推測的正確率。不使用指數衰減的學習率（即使用固定的學習率），實驗中使用了固定學習率為0.7和0.1兩種情況，固定學習率為0.7時的模型正確率與全優化模型的正確率非常接近，而固定學習率為0.1時的模型的正確率收斂較慢，不過在訓練一段時間后會逐漸接近全優化模型的正確率，但不如固定學習率為0.7的模型那么好。不使用正則化項或不使用滑動平均的模型的正確率，在此MNIST數據集上與全優化模型較為接近。

可見，設計神經網絡時（在硬件算力滿足情況下）最佳選擇是使用全優化模型，問題在于各優化策略對應參數該如何取值才能更好提高模型的正確率。以下研究全優化模型下各優化策略的參數取不同值時對模型正確率的影響，以選取最合理的參數值。

⑵ 激活函數對正確率的影響

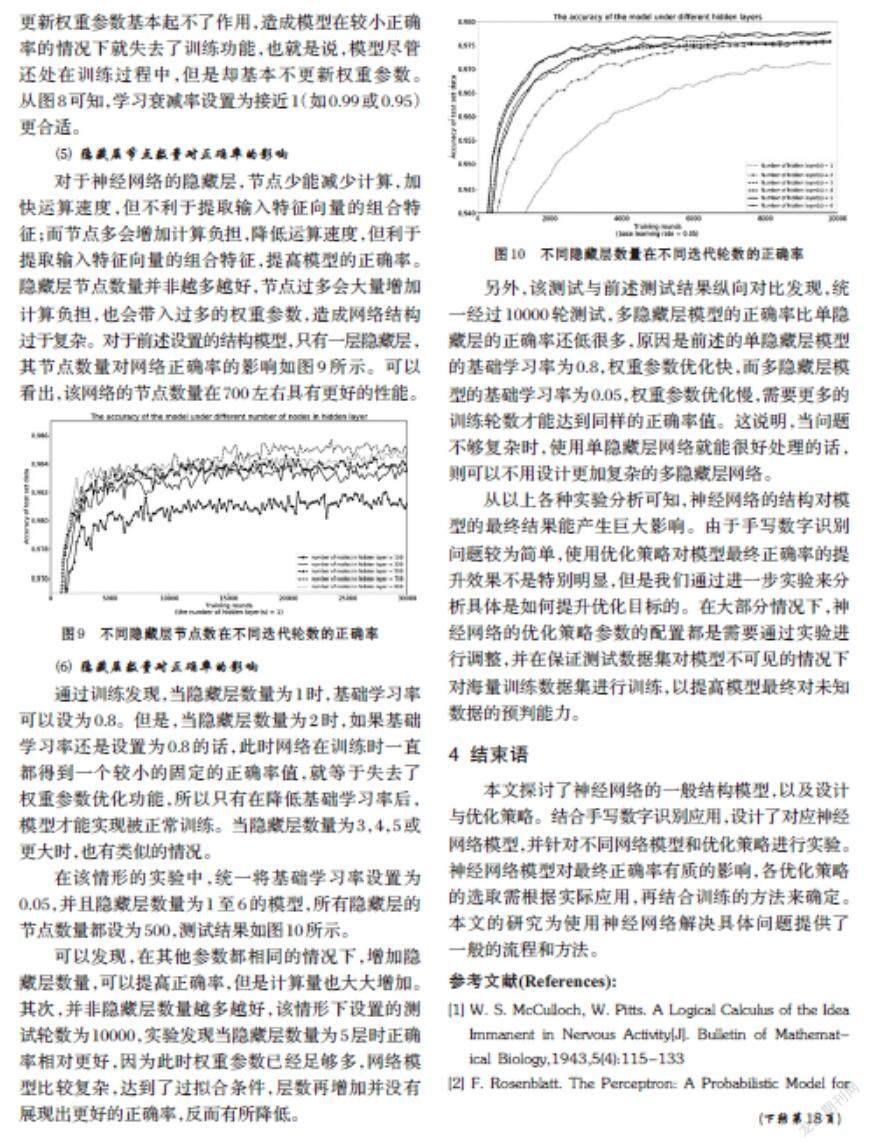
全優化模型下，分別使用三種常用激活函數[ReLU]、[tanh]和[sigmoid]對模型正確率的影響。對每種激活函數都進行多次訓練，然后從每種激活函數訓練結果中隨機選取三條，得到結果如圖5。使用[ReLU]激活函數的模型收斂最快，正確率也最高。

⑶ 基礎學習率對正確率的影響

全優化模型使用指數衰減的學習率，需確定基礎學習率和學習衰減率。基礎學習率取不同值時，分別進行多次訓練，模型正確率的收斂情況如圖6所示。

將基礎學習率取不同值訓練得到的正確率進行平均計算，結果如圖7所示。可以發現，當基礎學習率在0.8左右時，模型收斂性和正確率達到極優。

⑷ 學習衰減率對正確率的影響

設置模型具有相同基礎學習率0.8，探索不同學習衰減率對模型正確率的影響。

圖8顯示的是設置不同的學習衰減率時，對應的學習率衰減曲線和正確率曲線的關聯圖。學習衰減率通常小于1，從圖8可以看到，當學習衰減率值離1較遠（如為0.7）時，學習率衰減很快，在短時間會快速衰減到接近0，而過小的學習率在反向傳播算法中對更新權重參數基本起不了作用，造成模型在較小正確率的情況下就失去了訓練功能，也就是說，模型盡管還處在訓練過程中，但是卻基本不更新權重參數。從圖8可知，學習衰減率設置為接近1（如0.99或0.95）更合適。

⑸ 隱藏層節點數量對正確率的影響

對于神經網絡的隱藏層，節點少能減少計算，加快運算速度，但不利于提取輸入特征向量的組合特征;而節點多會增加計算負擔，降低運算速度，但利于提取輸入特征向量的組合特征，提高模型的正確率。隱藏層節點數量并非越多越好，節點過多會大量增加計算負擔，也會帶入過多的權重參數，造成網絡結構過于復雜。對于前述設置的結構模型，只有一層隱藏層，其節點數量對網絡正確率的影響如圖9所示。可以看出，該網絡的節點數量在700左右具有更好的性能。

⑹ 隱藏層數量對正確率的影響

通過訓練發現，當隱藏層數量為1時，基礎學習率可以設為0.8。但是，當隱藏層數量為2時，如果基礎學習率還是設置為0.8的話，此時網絡在訓練時一直都得到一個較小的固定的正確率值，就等于失去了權重參數優化功能，所以只有在降低基礎學習率后，模型才能實現被正常訓練。當隱藏層數量為3，4，5或更大時，也有類似的情況。

在該情形的實驗中，統一將基礎學習率設置為0.05，并且隱藏層數量為1至6的模型，所有隱藏層的節點數量都設為500，測試結果如圖10所示。

可以發現，在其他參數都相同的情況下，增加隱藏層數量，可以提高正確率，但是計算量也大大增加。其次，并非隱藏層數量越多越好，該情形下設置的測試輪數為10000，實驗發現當隱藏層數量為5層時正確率相對更好，因為此時權重參數已經足夠多，網絡模型比較復雜，達到了過擬合條件，層數再增加并沒有展現出更好的正確率，反而有所降低。

另外，該測試與前述測試結果縱向對比發現，統一經過10000輪測試，多隱藏層模型的正確率比單隱藏層的正確率還低很多，原因是前述的單隱藏層模型的基礎學習率為0.8，權重參數優化快，而多隱藏層模型的基礎學習率為0.05，權重參數優化慢，需要更多的訓練輪數才能達到同樣的正確率值。這說明，當問題不夠復雜時，使用單隱藏層網絡就能很好處理的話，則可以不用設計更加復雜的多隱藏層網絡。

從以上各種實驗分析可知，神經網絡的結構對模型的最終結果能產生巨大影響。由于手寫數字識別問題較為簡單，使用優化策略對模型最終正確率的提升效果不是特別明顯，但是我們通過進一步實驗來分析具體是如何提升優化目標的。在大部分情況下，神經網絡的優化策略參數的配置都是需要通過實驗進行調整，并在保證測試數據集對模型不可見的情況下對海量訓練數據集進行訓練，以提高模型最終對未知數據的預判能力。

4 結束語

本文探討了神經網絡的一般結構模型，以及設計與優化策略。結合手寫數字識別應用，設計了對應神經網絡模型，并針對不同網絡模型和優化策略進行實驗。神經網絡模型對最終正確率有質的影響，各優化策略的選取需根據實際應用，再結合訓練的方法來確定。本文的研究為使用神經網絡解決具體問題提供了一般的流程和方法。

參考文獻（References）：

[1] W. S. McCulloch， W. Pitts. A Logical Calculus of the Idea Immanent in Nervous Activity[J]. Bulletin of Mathematical Biology，1943，5（4）：115-133

[2] F. Rosenblatt. The Perceptron： A Probabilistic Model for Information Storage and Organization in the Brain[J]. Psychological Review，1958，65：386-408

[3] F. Rosenblatt. Principles of Neurodynamics： Perceptrons and the Theory of Brain Mechanisms[M]. Washington DC： Spartan Books，1962

[4] D. E. Rumelhart， G. E. Hinton， R. J. Williams. Learning Representations by Back Propagating Errors[J]. Nature，1986，323（6088）：533-536

[5] M. Minsky， S. A. Papert. Perceptrons： An Introduction to?Computational Geometry[M]. Massachusetts： MIT Press，1969

[6] 杜梅，趙懷慈.手寫數字識別的研究[J].計算機工程與設計，2010，31（15）：3464?3467

[7] 焦微微，巴力登，閆斌.手寫數字識別方法研究[J].軟件導刊，2012，11（12）：172?174

[8] 張黎，劉爭鳴，唐軍.基于BP神經網絡的手寫數字識別方法的實現[J].自動化與儀器儀表，2015（6）：169?170

[9] 陳浩翔，蔡建明，劉鏗然，等.手寫數字深度特征學習與識別[J].計算機技術與發展，2016，26（7）：19-23，29

[10] 陳玄，朱榮，王中元.基于融合卷積神經網絡模型的手寫數字識別[J].計算機工程，2017，43（11）：187-192

[11] 陳巖，李洋洋，余樂，等.基于卷積神經網絡的手寫體數字識別系統[J].微電子學與計算機，2018，35（2）：71?74

[12] 宋曉茹，吳雪，高嵩，等.基于深度神經網絡的手寫數字識別模擬研究[J].科學技術與工程，2019，19（5）：193?196

[13] 曾文獻，孟慶林，郭兆坤.基于深度卷積自編碼神經網絡的手寫數字識別研究[J].計算機應用研究，2020，37（4）：1?4

[14] Y. LeCun etc. The MNIST database of handwritten digits [EB/OL]. http：//yann.lecun.com/exdb/mnist.