基于交替迭代優化的同步調相機電氣參數分步辨識方法

王繼豪，王安東，孫福春，鄭競宏，曹志偉，朱文兵

(1. 國網山東省電力公司電力科學研究院，濟南 250003； 2. 清華大學 電機工程與應用電子技術系，北京 100084)

0 引 言

隨著特高壓直流輸電技術的大規模應用，交直流混合電網“強直弱交”的問題日益凸顯，必須配備大量動態無功補償裝置[1-3]。而300 Mvar大容量新型快速動態響應同步調相機的電氣參數經過優化設計，在動態無功補償方面具有明顯優勢[4]。同步調相機結構與同步電機相似，其暫態過程主要由其電氣參數決定，但廠家提供的模型和參數往往與其實際動態特性存在差異[5]，尤其是在大擾動時的動/暫態特性和非線性飽和特性。因此獲得準確的同步調相機模型及電氣參數是交直流混合電力系統分析、運行和控制的基礎。

目前，國內外學者提出了多種辨識同步電機參數的算法[6-11]，但實用化效果并不理想。同步電機待辨識參數多，同時辨識所有參數難度較大，易出現多值性和收斂性問題。若考慮同步電機的非線性飽和特性將進一步加劇多值性問題。

為此，有學者提出依據靈敏度大小逐步辨識參數。文獻[12]提出利用靈敏度辨識大小篩選出對電力系統動態過程影響較大的主導參數作為待估計參數集，以降低待辨識參數數量；文獻[13]進一步提出可以根據靈敏度的相位判斷參數的可辨識性；文獻[14]在靈敏度分析的基礎上，提出通過網格初始化搜索算法解決初值設置不合理導致的參數辨識多值性問題；文獻[15]通過分析不同擾動下同步發電機參數的靈敏度特征，制定了發電機參數分步辨識策略，提高瞬態/超瞬態參數辨識的準確性；文獻[16]利用短路實驗引起擾動，基于靈敏度分析確定主導參數進行分布辨識；文獻[17]利用甩負荷實驗，基于軌跡靈敏度確定合適的加權區間和權重系數，但沒有考慮飽和效應；文獻[18]利用勵磁階躍擾動，在頻域內采用分步辨識策略辨識發電機參數，也沒有考慮飽和效應。以上文獻均從理論角度闡述了基于靈敏度特征辨識同步電機參數的可行性，但存在以下問題：大部分文獻推薦采用短路大擾動實驗以提高參數辨識精度，但調相機位于換流站，難以開展此類大擾動實驗，有必要探究基于小擾動的參數辨識方法；不同擾動類型下的同步電機工況不同，基于單次擾動實驗數據辨識出的參數往往難以適用于其他擾動工況；相當一部分文獻沒有考慮同步電機飽和特性，而飽和特性恰恰是影響調相機動態、暫態/次暫態等性能的關鍵因素之一。

進一步分析，同步電機參數之間相互耦合，部分參數作用效果相反[9]。若同時辨識作用效果相反的參數，即使參數靈敏度大，也可能導致待辨識參數無法收斂至最優值。為此，可以將參數辨識看作優化問題，依據作用效果將待辨識參數分成幾組分步求解。而交替迭代乘子法(ADMM)作為一種求解此類優化問題的分散式方法，具有良好的收斂性、魯棒性，在電力系統經濟調度、微電網群調度等方面取得了良好的應用效果[19-20]。

針對以上問題，設計了適用于同步調相機的小擾動實驗方案。基于參數靈敏度分析法和ADMM法，采用三組小擾動實驗數據聯合辨識、穩態參數和暫態參數分步辨識的策略，完成現場實測驗證。

1 同步調相機模型及坐標變換

1.1 同步調相機數學模型

同步調相機內部結構及工作原理均與同步發電機類似[21]，主要區別在于同步調相機沒有原動力。因此，同步調相機的數學模型可以借鑒同步發電機的6階實用模型，其中電氣部分采用4階模型[22]，即：

(1)

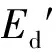
量測方程為：

(2)

式中id和iq分別為定子直軸和交軸電流分量。

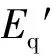
E′q0=KGE′q=(1+a(E′q)b-1)E′q=E′q+a(E′q)b

(3)

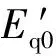
1.2 數據預處理

數據預處理分為： 數據濾波、計算有效值、標幺化、dq坐標變換。數據濾波通過高通濾波濾除功角、電壓、電流等測量數據中的高頻噪聲，減小對辨識效果的影響；dq坐標變換若按照通用的dq0坐標變換方法，需要知道調相機啟動瞬間轉子直軸與a相軸線初始角度a0或者功率因數角φ，但是初始角度a0往往不易準確測量，功角曲線的測量受轉速脈沖精度的影響會有相當的誤差。

針對同步調相機幾乎不發有功功率的特點，在功率因數角φ足夠小的情況下，考慮利用同步調相機定子側電壓Ua和線電流Ia的有效值代替Id和Uq，在對辨識結果影響不大的前提下，進一步簡化計算。

基于Simulink仿真調相機機端電壓擾動工況，仿真發現同步調相機的功角小于4°，實際及簡化處理得到的Id和Uq曲線基本重合，如圖1所示。基于以上兩組數據分別進行辨識調相機參數，辨識結果在誤差上基本沒有區別，進一步驗證了這種數據處理的可行性。下文均采用這種數據處理方式。

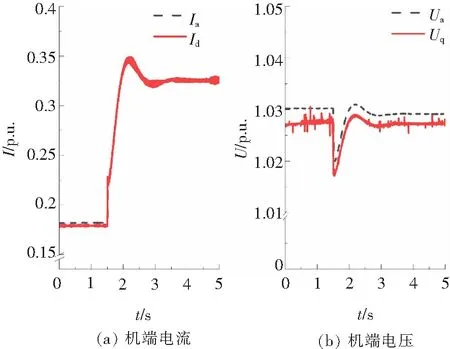
圖1 實際及簡化處后的Id和Uq曲線Fig.1 Actual and simplified curves of Id and Uq

2 同步調相機參數軌跡靈敏度分析

文獻[10]直接使用Simulink中的同步電機模塊進行靈敏度分析，所用模型與PSASP中的電機模型不兼容，而其所使用的辨識模型又與靈敏度分析所用模型不同，這導致了辨識過程中對參數的調整方向與靈敏度分析的規律存在區別，所制定的辨識策略在實際應用中出現收斂效率低、易陷入局部最優的問題。同時，同步調相機與傳統同步電機在參數范圍、擾動模式上(例如甩負荷擾動)均有較大區別，有必要依據辨識所用模型重新計算參數靈敏度。

參數對輸出的軌跡靈敏度定義如下：

(4)

式中y為系統輸出Id或Uq；θ為系統中的參數；Δθ為參數的相對改變量；t為時間。

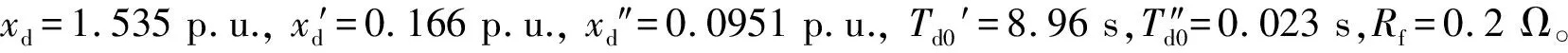
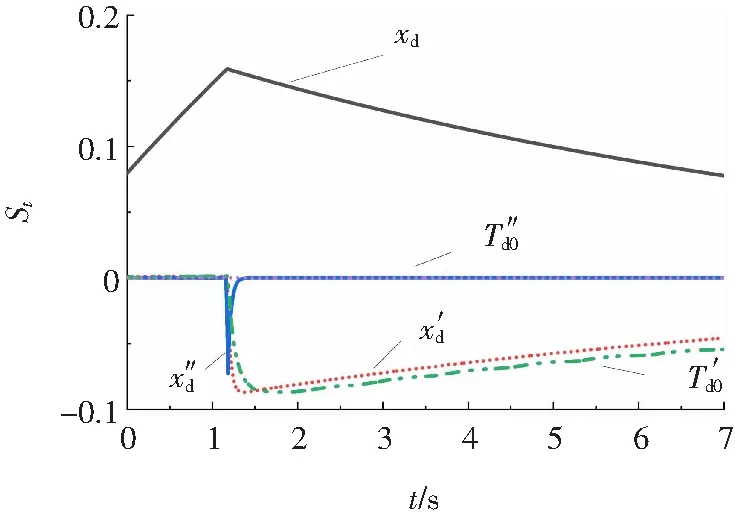
圖2 甩負荷擾動下各參數軌跡靈敏度Fig.2 Trajectory sensitivity of parameters in load rejection disturbance

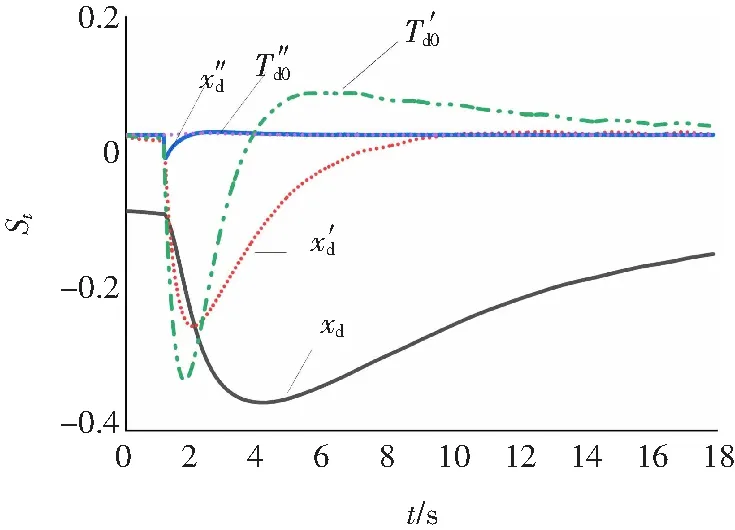
圖3 勵磁階躍擾動下各參數軌跡靈敏度Fig.3 Trajectory sensitivity of parameters in excitation step disturbance

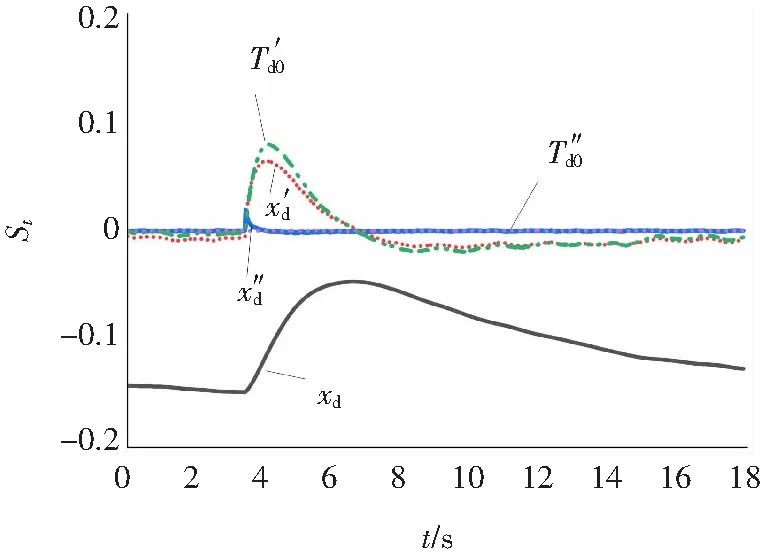
圖4 機端電壓擾動下各參數軌跡靈敏度Fig.4 Trajectory sensitivity of parameters in terminal voltage disturbance

分析圖2～圖4，可知各參數的靈敏度規律為：

(1)xd的靈敏度在三種擾動的整個過程中均比較大，從數值大小排序來看，階躍擾動的靈敏度(0.1～0.5)>機端電壓擾動的靈敏度(0.1～0.2)& 甩負荷擾動的靈敏度(0.1～0.2)；

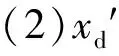
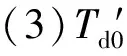
(4)xd″ 只在甩負荷后的瞬間靈敏度較大，在其余均非常小，在其他兩種擾動中的整個動態過程中靈敏度也非常小；

(5)Td0″ 在三種擾動的整個動態過程中靈敏度均非常小。

3 同步調相機辨識算法及策略

3.1 辨識算法

采用修正阻尼最小二乘法(Modified Damped Square, MDLS)辨識同步調相機參數。以實測實驗數據與擬合數據的誤差和為目標函數，即：

(5)

式中w1、w2、w3分別為甩負荷、勵磁階躍和機端電壓擾動對目標函數貢獻的比例系數；Uq、Id1、Id2為三種擾動下的擬合數據；Uq0、Id10、Id20為三種擾動下的實測數據；N1、N2、N3為三種擾動下的數據長度。

3.2 ADMM基本原理

參數辨識類問題可以看作優化問題，而ADMM法是一種求解優化問題的計算框架，適用于求解分布式凸優化問題，能夠降低問題規模和難度[24-25]。ADMM要解決的優化問題一般表述為：

(6)

式中x、z是優化變量；f(x)和g(z)是對應目標函數。

該類優化問題的求解步驟如下：

(1)求解與x相關的最小化問題，更新變量x；

(2)求解與z相關的最小化問題，更新變量z；

(3)更新迭代優化中需要的對偶變量，然后重復以上步驟。

可以看出，ADMM的核心思想是將規模大、難度高的全局問題分解為規模小、求解相對容易的局部子問題，通過交叉迭代優化協調子問題的解，最終得到大的全局問題的解，可以應用于待辨識參數較多的參數辨識問題。

3.3 分步聯合辨識策略

文獻[16-18]在辨識參數過程中只使用單擾動實驗數據，但文中研究發現，單擾動數據辨識出的參數可能并不能復現其他擾動類型。文獻[10]雖然采用多種擾動數據辨識參數，但每一步驟只使用單一擾動辨識單個參數，辨識過程復雜。考慮到穩態參數影響整個擾動過程，暫態/次暫態參數主要影響擾動瞬間的動態過程。基于上面的軌跡靈敏度分析，借鑒ADMM交叉迭代的思想，提出了一套實用化的分步聯合辨識策略，采用三組擾動實驗數據同時辨識參數，穩態、暫態/次暫態參數分步辨識，通過交替迭代的方式提高參數辨識準確性。

圖5給出了參數辨識流程圖，具體步驟如下：

(1)預辨識所有參數：為保證辨識的效果，需要給分步辨識設置一個合適的辨識初值，而設計值并不一定合適。勵磁階躍和機端電壓擾動的作用效果主要體現在機端電壓上，二者作用效果接近，且勵磁階躍軌跡靈敏度略大于機端電壓擾動下的參數軌跡靈敏度。故第一步選擇以甩負荷和勵磁階躍擾動的整個擾動數據為主，預辨識所有參數，并將辨識結果作為正式開始辨識的參數初值，設置w1：w2：w3=0.5：0.4：0.1；

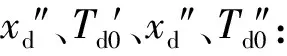
(4)整體修正辨識參數：考慮到穩態和暫態類參數并不是完全割裂的，其相互間存在很強的相互影響，因此增加一步辨識，以融合所有參數的相互影響，該過程主要起一個整體修正作用。勵磁階躍擾動和機端電壓擾動的參數靈敏度規律接近，且勵磁階躍擾動的參數靈敏度更大。因此，可選擇甩負荷擾動數據和勵磁階躍擾動的整個擾動數據為主辨識所有參數，設置w1：w2：w3=0.5：0.4：0.1；

(5)步驟(2)～步驟(4)交替迭代2～5次；

(6)微調：完成迭代后，在0.9倍～1.1倍參數范圍內整體微調再次辨識，以保證所有參數均在合理范圍內，設置w1：w2：w3=0.4：0.1：0.5。

在參數軌跡靈敏度分析的基礎上，三種擾動的具體比例關系可在多次調整后根據辨識效果最終確定。

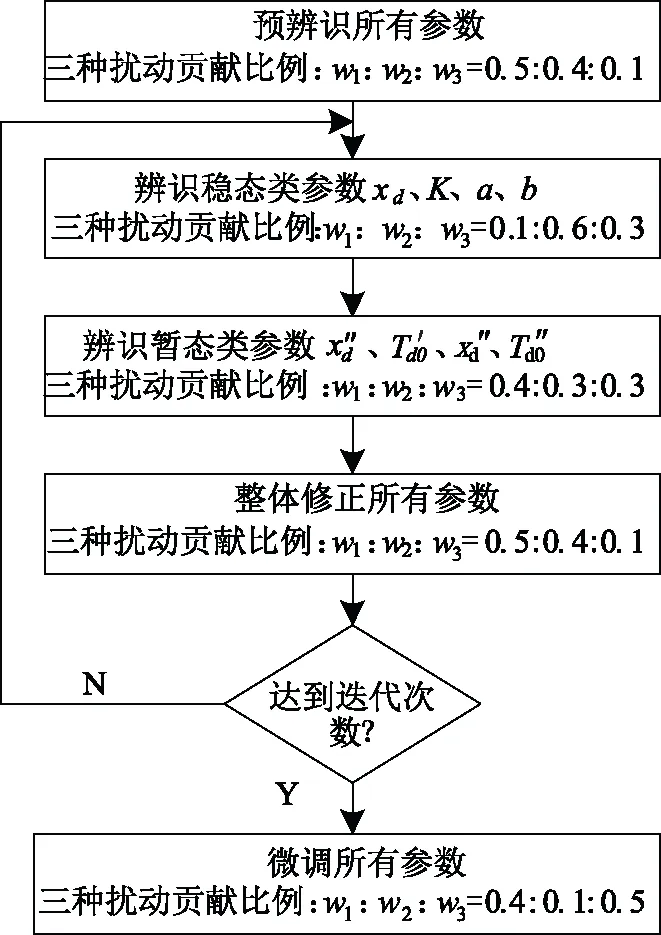
圖5 參數辨識流程圖Fig.5 Flow chart of parameter identification

4 參數辨識驗證

4.1 實驗測試方案

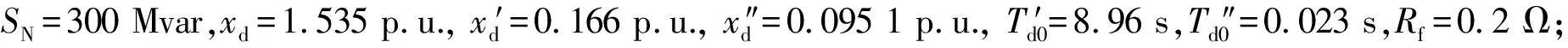
擾動實驗測試方案包括：

(1)勵磁階躍擾動：維持同步調相機無功出力不變，改變勵磁調節器給定值，在勵磁回路中施加一個使機端電壓波動大于2%的擾動量；

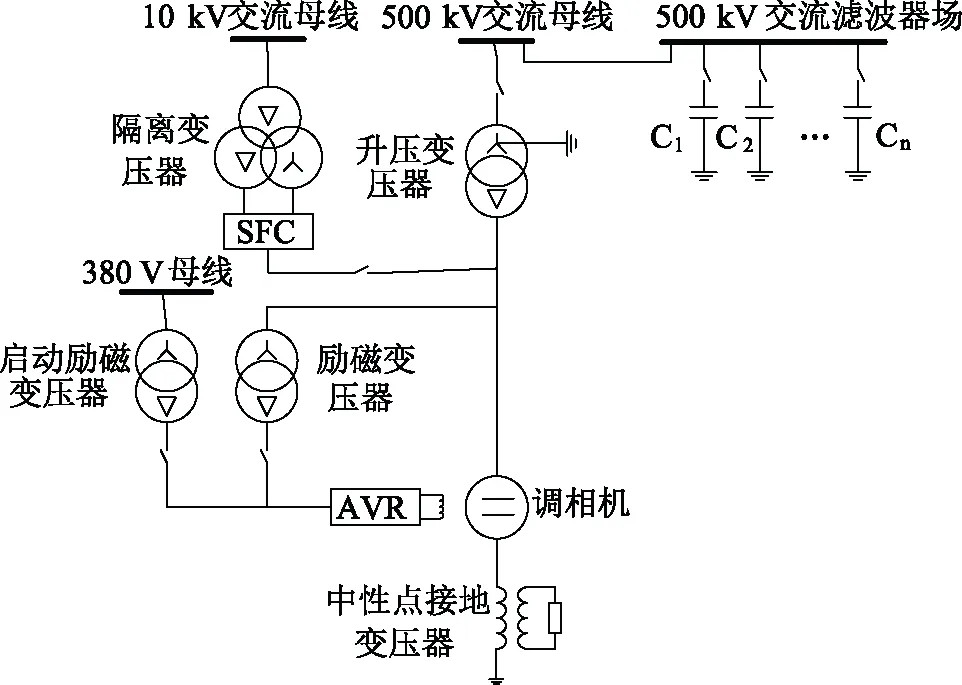
圖6 系統簡化電路圖Fig.6 Simplified system circuit diagram

(2)機端電壓擾動：由于同步調相機通過升壓變壓器直接連接在換流站交流母線上，緊靠換流閥，進行短路等大擾動實驗的安全風險大，故采用投切電容器的方式造成機端電壓擾動。維持同步調相機無功出力不變，在機端依次投切255 Mvar、210 Mvar、210 Mvar三組電容器組，施加一個使機端電壓波動大于2%的擾動量；

(3)甩負荷擾動實驗：令同步調相機進相-150 Mvar運行，突然切機甩負荷產生擾動。

4.2 參數辨識驗證

選取50 Mvar+3%勵磁階躍、投一組210 Mvar電容器組、-150 Mvar甩負荷三組擾動實驗數據，依據圖5所示辨識流程依次辨識同步調相機參數。

(1)獲得辨識起點；預辨識結果見表1和圖7。

表1 參數預辨識結果Tab.1 Pre-identification result of all parameters

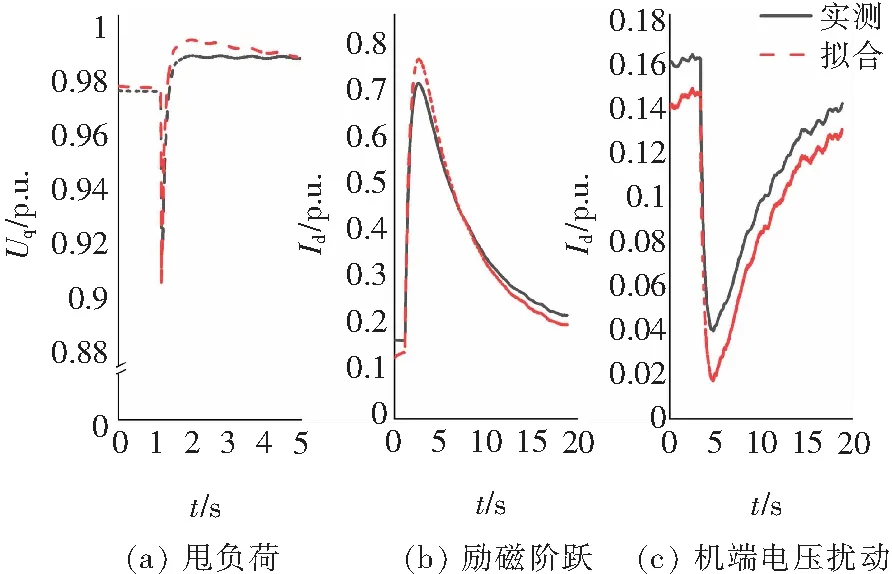
圖7 三種擾動下的擬合曲線(預辨識)Fig.7 Fitting curves under three disturbances (Pre-identification)

(2)辨識xd、a、b；

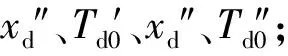
(4)整體修正辨識參數；

(5)迭代步驟(2)～步驟(4)約2～5次；

(6)微調所有參數獲得最終結果。

辨識結果見表2和圖8。

表2 微調后參數辨識結果Tab.2 Parameter adjustment result after fine adjustment

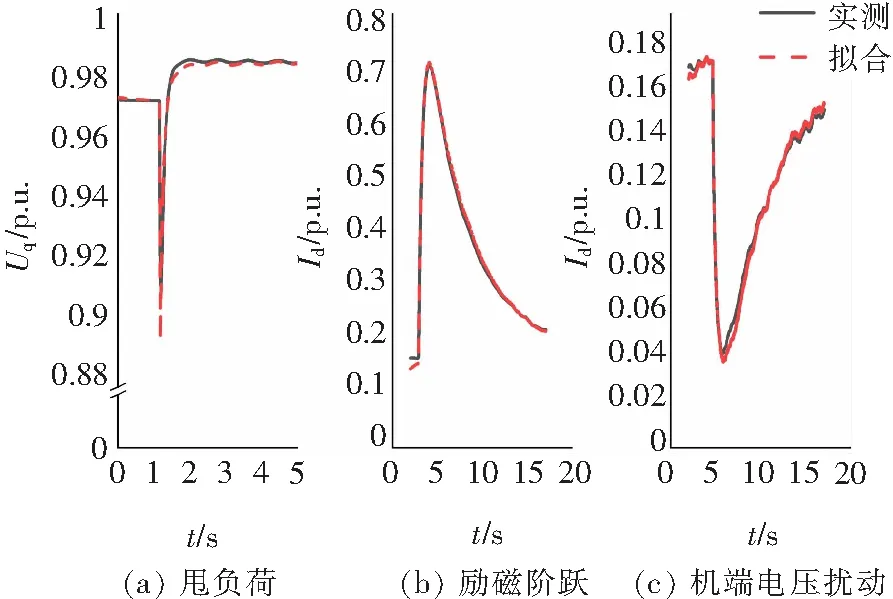
圖8 三種擾動下的擬合曲線(微調后)Fig.8 Fitting curves under three disturbances (arter fine adjustment)

分析圖8可以看出，擬合曲線與實測曲線十分接近，說明所提的分步聯合辨識策略效果良好。

4.3 多種參數辨識策略比較

為了說明上述同步調相機參數分步聯合辨識策略的有效性，分別利用廠家提供的參數設計值、分步聯合辨識策略辨識出的參數、單次擾動辨識出的參數、利用三組擾動數據一次性辨識出的參數擬合實測數據，計算擬合曲線與實測曲線的均方根誤差。結果見表3。

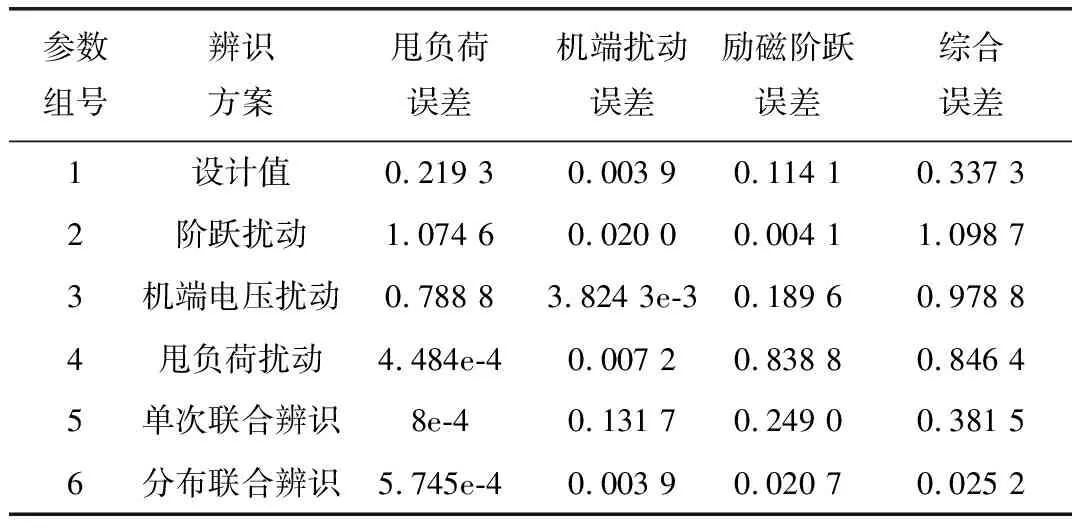
表3 辨識結果對多種擾動的誤差分析Tab.3 Error analysis of identification result for several disturbances

分析表3可知，采用單次擾動辨識出的參數不能保證對其他兩類擾動的擬合效果(2組、3組、4組)；利用三種擾動數據一次辨識出所有參數的效果略有所改善(5組)，但有提升空間；采用分布聯合辨識策略辨識出的參數能準確復現所有擾動實測結果，獲得比設計值和單擾動辨識方法、單次聯合辨識方法更好的效果；分步聯合辨識策略由于兼顧了甩負荷、勵磁階躍和機端電壓擾動的動態特性，所得結果具有更小的綜合誤差，其結果具有更好的適用性。

5 結束語

提出了一種適用于同步調相機的電氣參數辨識方法，所做的工作主要有：

(1)建立了考慮飽和特性的同步調相機數學模型。通過高通濾波對數據進行預處理，針對調相機不發有功功率的特點，確定了利用Ua和Ia代替Id和Uq的數據簡化處理方式；

(2)針對換流站實際運行工況，設計了適用于現場操作的同步調相機小擾動實驗方案；

(3)通過參數軌跡靈敏度，分析確定辨識參數的最佳擾動組合。將ADMM的思想引入參數辨識中，提出了實用化的調相機參數分步聯合辨識方法，并將其成功地應用到伊克昭-沂南直流送電工程中。

研究表明，三組實驗聯合辨識優于單擾動辨識，分步辨識優于一次性辨識所有參數。其很好地解決了基于單次擾動實驗辨識出的參數無法復現其他工況實驗數據的問題，提高了參數辨識結果的適用性和準確性。