多形態擬合水下潛器欠驅動運動控制與目標跟蹤

辛光紅 陳曉虎 韓建芳

(三亞學院，海南三亞 572000)

1 概述

多形態擬合水下潛器（以下簡稱ARG）因為系統中只有質量塊位移和航向角作為控制輸入，在空間運動控制中是一個典型的欠驅動系統。同時,在目標跟蹤控制問題中即使沒有姿態的約束,雖然也有三個位置偏差需要控制,但仍然多于控制輸入的數量。欠驅動系統是指空間維數低于構形空間維數的控制系統,或指令輸入低于控制系統控制自由度的控制系統。欠驅動控制水下潛器, 是一個輸入維數遠小于控制系統自由度的零點五自主水下機器人[1]。為了完成精確的水下任務，具有六自由度和全自由度運動的自主水下航行器通常需要配備多個推進器。按照深水下潛器的驅動特點,把水下航行體分成欠驅動、過驅動和全驅動二種型式[4-5]。本文在進行目標跟蹤控制時，根據執行機構的特點，合理地描述潛器與目標點之間的位置關系。然后，再受力分析得到數學關系，構造出實現目標跟蹤的性能指標函數項。如圖1 所示，輸入- 輸出推力反饋圖反映了六自由度水下航行器控制系統與輸出系統之間的關系。

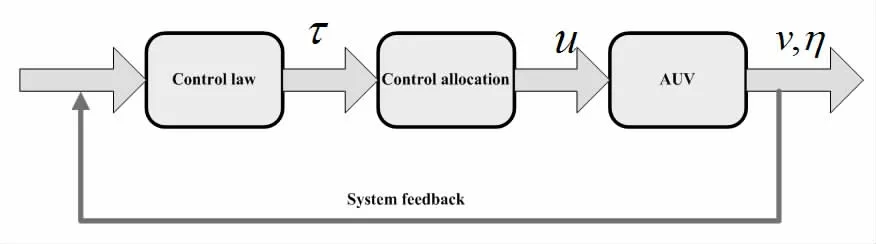
圖1 推力反饋圖

2 欠驅動水平運動控制

對欠驅動水下機器人三自由度水平運動方程與軌道方程的簡化,并設計了自動診定與穩定控制器。通過全局微分與同胚坐標轉換, 把欠驅動水下機器人的數學模型轉換成級聯非線性系統[2]。證實了原網絡系統的診斷為問題,可簡化成級聯子系統的診斷為問題。通過對狀態反饋控制器的研究,對該控制器的自診定控律進行了數學描述,并證實了該控律的收斂性,而仿真試驗則證實了該控制器的自診定性能[3]。

水下機器人船體慣性坐標系與動力參考坐標系轉換的運動學方程為:

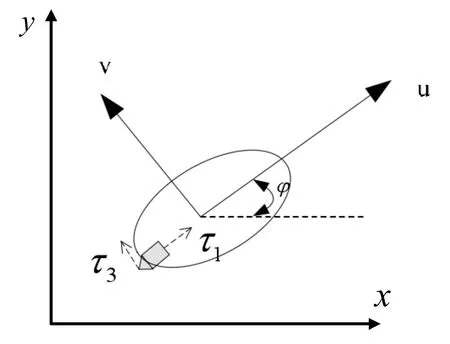
圖2 ARG 平面運動坐標系

3 垂直運動控制及跟蹤控制

本文運動軌跡控制均假設為與時間無相關曲線參數進行描述。在欠驅動控制下，ARG 從任意初始位置以所需速度按預設參數曲線運動。收水下潛器能量消耗約束，大多數水下潛器設計為回轉體結構，僅保留縱向速度及俯仰角速度可控，水下潛實現器垂向運動及路徑跟蹤控制是設計的難點。垂直面自適應性模糊反步滑模路徑跟蹤控制器設計原理如下：

3.1 設計速度自適應模糊反步滑模控制器

縱向速度控制器為：

為了實現水下潛器跟蹤誤差收斂，對于H1 取值令| Q1| >0，當Q1= h1時滿足縱向速度滿足收斂誤差。

3.2 設計俯仰角自適應的模糊反步滑模控制器

設計俯仰角自適應模糊反步滑模控制器設計如（7）、（8）式子所示：

通過上述（1）（2）兩步，實現速度誤差和航向角誤差跟蹤收斂。

4 仿真分析

為了驗證所設計的垂向運動及跟蹤控制器的有效性，利用MATLAB/SIMULINK 對多形態擬合水下潛器進行了仿真。以標稱模型用作被控制對象。

假設水下潛器在水平和垂直三維坐標下分別受到5N/m 的外部干擾，以表1 所示參數進行直線和正弦路徑跟蹤。直線路徑的參數方程為：

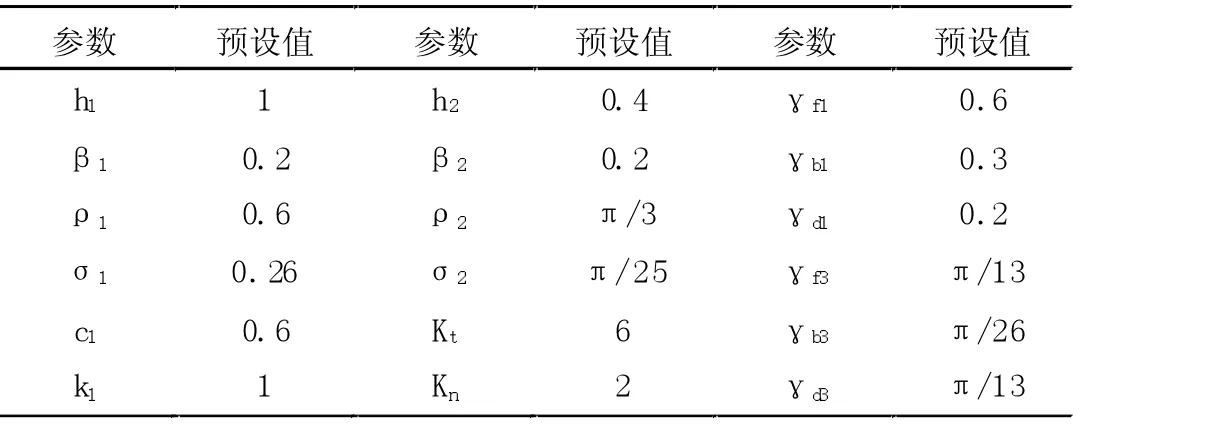
表1 垂向跟蹤預設參數

正弦路徑跟蹤曲線和縱向速度控制曲線分別如圖5、6 所示。

通過仿真驗證圖3～6 表明，在ARG 仿真模型在受外界干擾的情況下，所設計的垂向路徑控制器能夠快速收斂水下航行體的縱向速度至期望值。實現了水下潛器欠驅動垂向運動路徑跟蹤，設計的控制器路徑跟蹤誤差較快的實現了歸零收斂。在控制性能方面，直線和正弦曲線跟蹤過程中，潛器器的最大俯仰角分別為23.7 度和19.2 度，基本滿足俯仰調節閾值要求。除上述追蹤軌道外,能夠選擇同樣的限制技術參數,體現了控制器優秀的自動適應能力與魯棒性。

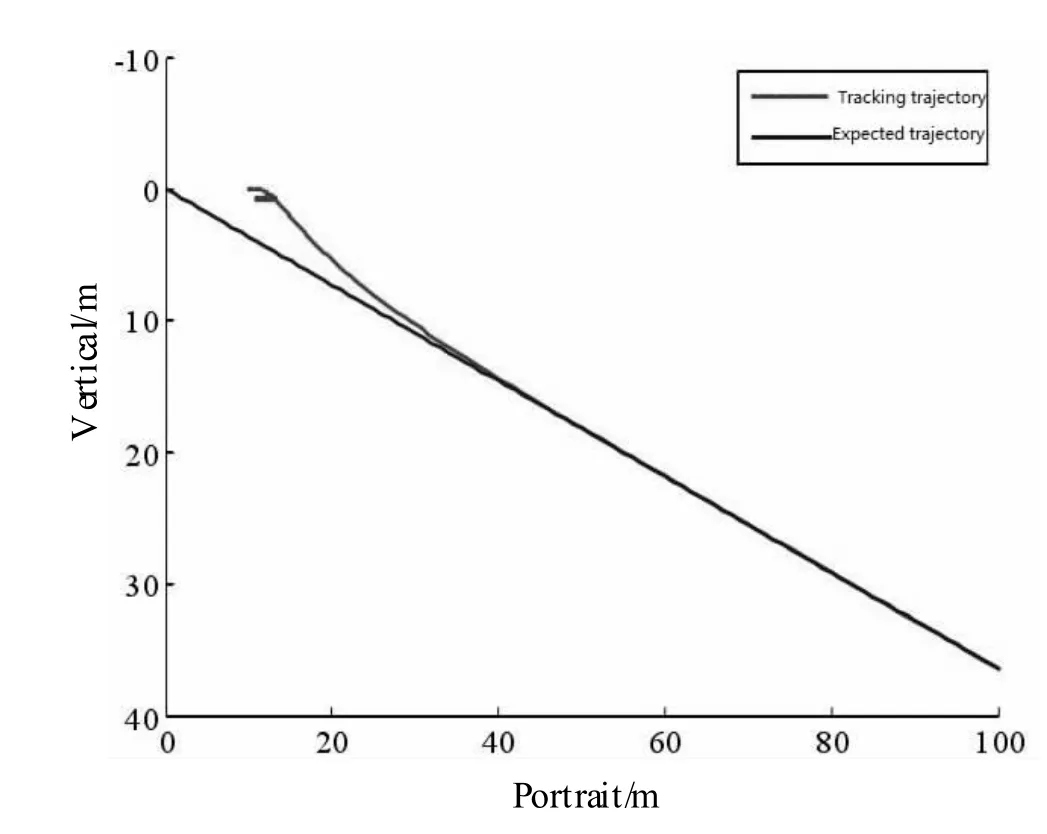
圖3 直線路徑跟蹤曲線

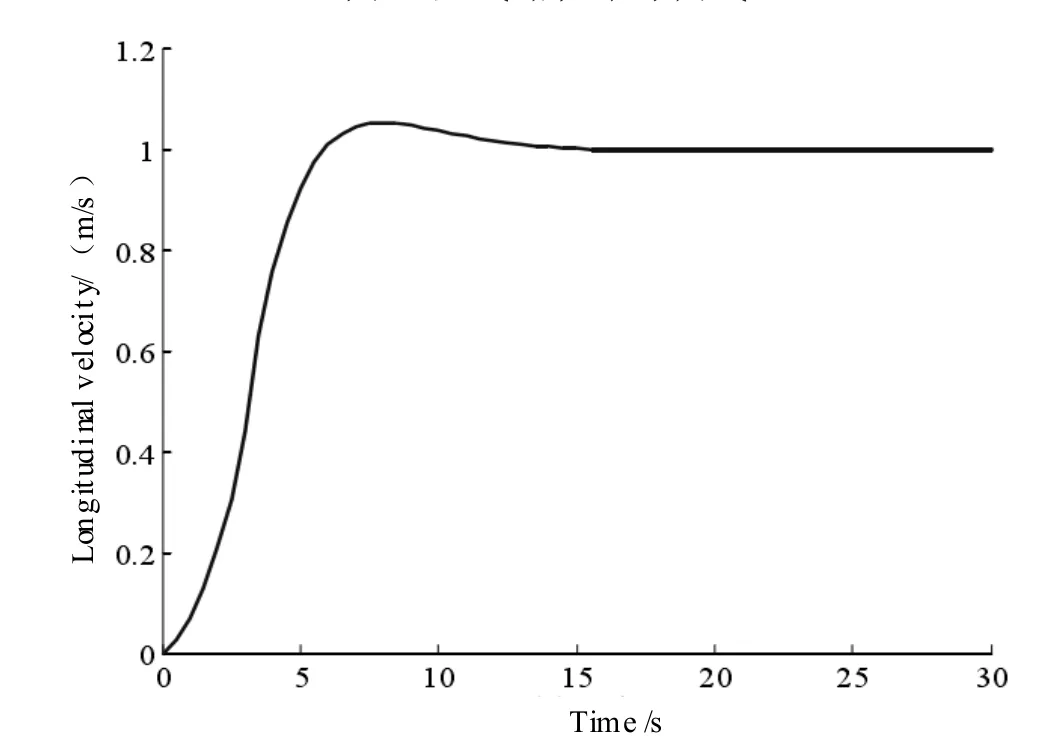
圖4 直線縱向速度控制曲線

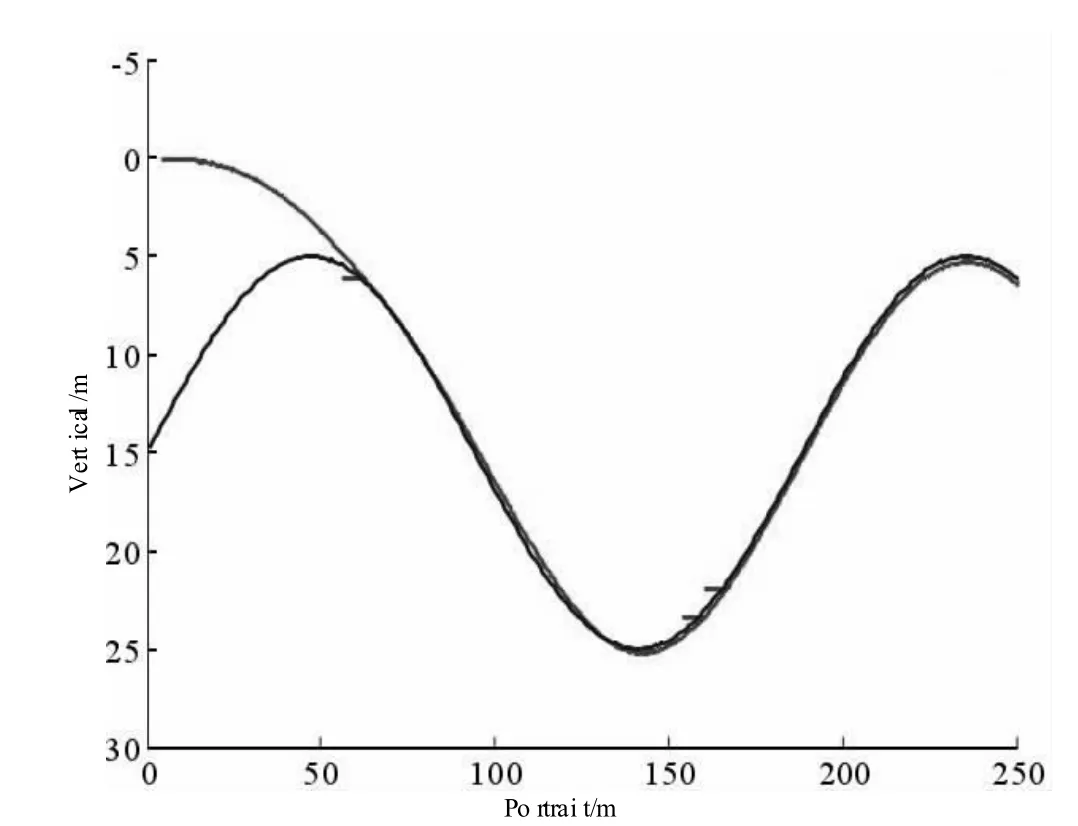
圖5 正弦路徑跟蹤曲線

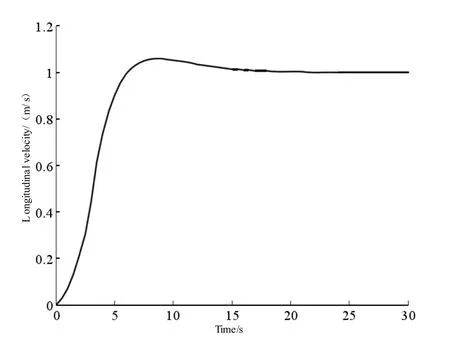
圖6 正弦縱向速度控制曲線

5 結論

水下潛器的欠驅動控制技術已經在基礎理論研究與實踐運用方面獲得了一定成績,欠驅動工業機器人的非線性空間公平、非線性能控性與結構能控性的理論研發也獲得了很大發展,但相關理論還在不斷發展完善，水下潛器欠驅動控制理論體系仍有較大發展空間和不足，如因為欠驅動系統的非完整約束帶來的下潛器無法實現跟蹤全坐標空間軌跡曲線等問題亟需解決。此外，欠驅動水下潛器空間目標跟蹤問題需要引入更豐富的設計方法進行工程驗證。故, 進一步提出新的控制方式和理論方法,不斷發展應欠驅動水下機器人技術的理論體系,并進行系統運動規劃與軌跡追蹤工程實踐, 是欠驅水下潛器研究的新發展趨勢。