通信延時(shí)環(huán)境下異質(zhì)網(wǎng)聯(lián)車輛隊(duì)列非線性縱向控制
李永福 何昌鵬 朱 浩 鄭太雄
道路交通運(yùn)輸是國(guó)民經(jīng)濟(jì)的血脈,但現(xiàn)有道路基礎(chǔ)設(shè)施難以擴(kuò)展,由于道路通行能力不足和汽車保有量迅速增加而引起的交通擁堵、尾氣污染等問題使交管部門面臨嚴(yán)峻的挑戰(zhàn).隨著自動(dòng)駕駛技術(shù)和V2V (Vehicle-to-vehicle)通信技術(shù)的迅猛發(fā)展,傳統(tǒng)的自適應(yīng)巡航控制ACC (Adaptive cruise control,ACC)逐漸發(fā)展成為協(xié)同自適應(yīng)巡航控制 (Cooperative adaptive cruise control,CACC).它利用V2V 通信技術(shù)共享車輛狀態(tài)(位置、速度、加速度)信息,提升了車輛隊(duì)列的穩(wěn)定性并降低了反應(yīng)延遲[1].研究表明,車輛以隊(duì)列模式行駛可有效提高道路通行效率、車輛燃油經(jīng)濟(jì)性和行駛安全性[2-3].因此,從改善車輛行駛模式的角度研究車輛隊(duì)列系統(tǒng)的控制方法,以提高道路通行效率和車輛燃油利用率,具有巨大的應(yīng)用價(jià)值和研究意義.
車輛隊(duì)列控制的目標(biāo)是使隊(duì)列中車輛保持等間距勻速行駛,且要求相鄰兩車不能發(fā)生碰撞[4].然而通信拓?fù)浣Y(jié)構(gòu)的改變以及通信延時(shí)或丟包的存在可能導(dǎo)致隊(duì)列中車輛速度振蕩,從而引起隊(duì)列不穩(wěn)定.諸多學(xué)者針對(duì)這一問題開展了廣泛研究[5-12].文獻(xiàn)[5]針對(duì)Ad-hoc 型車輛網(wǎng)絡(luò)的容量限制和Bernoulli隨機(jī)丟包問題,提出了一種車輛編隊(duì)算法,解決了網(wǎng)絡(luò)沖突并保證了車輛隊(duì)列的弦穩(wěn)定性.考慮輸入延時(shí)和前車間距,文獻(xiàn)[6]提出一種僅依靠車載傳感器感知信息的車輛隊(duì)列控制器,并得出了延時(shí)邊界和弦穩(wěn)定性條件.利用矩陣特征值分析方法,文獻(xiàn)[7]針對(duì)多種通信拓?fù)浣Y(jié)構(gòu)對(duì)車輛隊(duì)列穩(wěn)定性和擴(kuò)展性進(jìn)行分析,得到了其穩(wěn)定條件.針對(duì)通信拓?fù)淝袚Q問題,文獻(xiàn)[8]提出一種考慮有限時(shí)間穩(wěn)定的非線性車輛隊(duì)列控制器,實(shí)現(xiàn)了固定通信拓?fù)浜颓袚Q通信拓?fù)湎碌能囕v隊(duì)列控制.通過引入Markov模型描述網(wǎng)絡(luò)的隨機(jī)接入過程,文獻(xiàn)[9]提出一種適應(yīng)信道衰落條件下的車輛隊(duì)列控制算法.文獻(xiàn)[10]充分討論了通信延時(shí)對(duì)幾種主要車輛隊(duì)列控制方法的影響,結(jié)論表明領(lǐng)導(dǎo)車輛與跟隨車輛狀態(tài)信息的傳遞結(jié)構(gòu)決定了車輛隊(duì)列的弦穩(wěn)定性,而與車輛動(dòng)力學(xué)和控制器設(shè)計(jì)無(wú)關(guān).文獻(xiàn)[11]考慮動(dòng)力傳動(dòng)系統(tǒng)延時(shí)并引入事件驅(qū)動(dòng)機(jī)制提出一種適用于Adhoc 網(wǎng)聯(lián)車輛隊(duì)列的反饋控制器.考慮IEEE 802.11P 協(xié)議真實(shí)環(huán)境下的通信延時(shí),文獻(xiàn)[12]基于一致性協(xié)議提出一種車輛隊(duì)列控制方法,其分析和實(shí)驗(yàn)結(jié)果表明領(lǐng)導(dǎo)車輛信息的全局可達(dá)對(duì)于車輛隊(duì)列的穩(wěn)定性至關(guān)重要.文獻(xiàn)[13]考慮領(lǐng)導(dǎo)車輛的加速度擾動(dòng)和風(fēng)阻,提出基于一種分層混合模型的魯棒延時(shí)車輛隊(duì)列控制器,并保證了車輛隊(duì)列的弦穩(wěn)定性.然而,由于未考慮行車安全,基于上述研究的車輛隊(duì)列控制可能導(dǎo)致相鄰車輛間出現(xiàn)碰撞問題.
從車輛隊(duì)列的勻質(zhì)/異質(zhì)性角度來看,許多與車輛隊(duì)列控制有關(guān)的研究均假設(shè)車輛隊(duì)列為勻質(zhì)隊(duì)列.針對(duì)勻質(zhì)車輛隊(duì)列的協(xié)同控制問題,文獻(xiàn)[14]利用網(wǎng)聯(lián)環(huán)境下隊(duì)列中的一致性和隊(duì)列間的群一致性,提出一種新的勻質(zhì)車輛多隊(duì)列協(xié)同控制器.文獻(xiàn)[15]基于分層模糊邏輯,提出了一種融合滑模控制和模糊控制的雙層變結(jié)構(gòu)控制方法.事實(shí)上勻質(zhì)車輛隊(duì)列的假設(shè)過于理想化,因?yàn)檎鎸?shí)交通場(chǎng)景中車輛通常是異質(zhì)的,因此部分學(xué)者對(duì)異質(zhì)車輛隊(duì)列展開了研究.考慮車輛動(dòng)力學(xué)因素,文獻(xiàn)[16] 提出一種三階異質(zhì)車輛隊(duì)列協(xié)同控制器,并引入了基于代數(shù)黎卡提方程的綜合分析方法,得到了控制增益的穩(wěn)定性區(qū)域.針對(duì)智能車輛傳感器失效和采樣周期影響的問題,文獻(xiàn)[17]提出一種適應(yīng)切換延時(shí)系統(tǒng)的異質(zhì)車輛隊(duì)列控制方法,保證了隊(duì)列行駛的一致性.文獻(xiàn)[18]基于事件驅(qū)動(dòng)機(jī)制提出滿足通信資源有效性和弦穩(wěn)定性的異質(zhì)車輛隊(duì)列控制方法.針對(duì)參數(shù)不確定性問題,文獻(xiàn)[19]基于反步法提出一種車輛隊(duì)列控制策略,同時(shí)滿足隊(duì)列的內(nèi)部穩(wěn)定和弦穩(wěn)定.利用車輛的異質(zhì)特性使隊(duì)列控制更加符合實(shí)際,但交通流中車輛間的非線性相互作用的影響并未在控制器中考慮.
隨著車輛隊(duì)列控制理論的逐步發(fā)展,車輛碰撞風(fēng)險(xiǎn)的研究引起了學(xué)者的關(guān)注[20-22].文獻(xiàn)[20]分析得出避免發(fā)生碰撞時(shí)車輛隊(duì)列控制器設(shè)計(jì)應(yīng)滿足的四個(gè)條件,并具體給出了幾種控制因素影響下的控制器設(shè)計(jì)方法.考慮車輛制動(dòng)場(chǎng)景,文獻(xiàn)[21]提出一種積分滑模控制器,保證車輛隊(duì)列行駛過程中避免發(fā)生碰撞.文獻(xiàn)[22]基于二階積分模型,提出一種非線性車輛隊(duì)列控制器,避免了車輛間的碰撞.然而,上述文獻(xiàn)并未對(duì)車輛動(dòng)力學(xué)的異質(zhì)特性和交通流中車輛跟馳行為對(duì)車輛隊(duì)列控制的影響進(jìn)行全面地描述.
本文旨在研究通信延時(shí)環(huán)境下的車輛隊(duì)列協(xié)同控制方法.考慮通信延時(shí)和車輛異質(zhì)特性,基于車輛動(dòng)力學(xué)模型,提出一種新的車輛隊(duì)列非線性控制器,并深入分析通信延時(shí)對(duì)車輛隊(duì)列穩(wěn)定性的影響.本文的主要?jiǎng)?chuàng)新點(diǎn)包括:1)與現(xiàn)有文獻(xiàn)[6-7,9-14,16-20]中設(shè)計(jì)的車輛隊(duì)列線性控制器不同,本文提出一種基于車輛三階動(dòng)力學(xué)模型的非線性隊(duì)列控制器;2)本文所設(shè)計(jì)的隊(duì)列控制器,考慮了車輛間的跟馳作用關(guān)系,避免出現(xiàn)負(fù)的車輛間距和不合理的加/減速度,提高行車安全和舒適度,保證車輛的運(yùn)動(dòng)行為符合交通流理論;3)考慮了異質(zhì)通信延時(shí)和異質(zhì)車輛特性對(duì)車輛隊(duì)列控制的影響,并利用Lyapunov-Krasovskii 定理分析得出了通信延時(shí)上界,保證了隊(duì)列行駛的穩(wěn)定性.
本文結(jié)構(gòu)如下:第1 節(jié)為問題描述及模型建立,描述了車輛隊(duì)列控制問題和通信拓?fù)浣Y(jié)構(gòu)表征并建立了車輛動(dòng)力學(xué)模型;第2 節(jié)設(shè)計(jì)了考慮異質(zhì)通信延時(shí)的非線性異質(zhì)車輛隊(duì)列協(xié)同控制器,并進(jìn)行了穩(wěn)定性和通信延時(shí)上界分析;第3 節(jié)進(jìn)行了不同通信拓?fù)浣Y(jié)構(gòu)和有/無(wú)通信延時(shí)情形下的對(duì)比數(shù)值仿真驗(yàn)證和分析;第4 節(jié)進(jìn)行總結(jié).
1 問題描述及模型建立
1.1 問題描述
如圖1 所示交通場(chǎng)景,考慮N+1 輛車組成的異質(zhì)車輛隊(duì)列,領(lǐng)導(dǎo)車輛編號(hào)i=0,跟隨車輛編號(hào)i=1,2,···,N,車身長(zhǎng)度用l表示.通過V2V 通信技術(shù),隊(duì)列中的車輛能夠相互交換狀態(tài)信息(位置p,速度v,加速度a),也可以通過激光雷達(dá)等距離傳感器獲取與前車的間距d.車輛的通信拓?fù)浣Y(jié)構(gòu)采用代數(shù)圖論進(jìn)行描述.將隊(duì)列中跟隨車間的通信拓?fù)涑橄鬄橐粋€(gè)連通圖G(V,E,A),其中V={1,···,N}為圖G中節(jié)點(diǎn)的集合,E?V ×V表示圖G中兩兩節(jié)點(diǎn)的邊集,即跟隨車輛間的通信連接.A=[aij]N×N為連接矩陣,aij=1 表示車輛i與車輛j有通信連接,aij=0 表表示車輛i與車輛j未建立通信連接.Ψ=[ρ10,···,ρN0]T為跟隨者車輛與領(lǐng)導(dǎo)車輛的連接矩陣,即與領(lǐng)導(dǎo)車輛的通信連接,ρi0=1表示i車與領(lǐng)導(dǎo)車輛建立通信連接,ρi0=0表示i車與領(lǐng)導(dǎo)車輛未建立通信連接.典型的前車-領(lǐng)導(dǎo)跟隨式(Predecessor-leader following type,PLF)和雙前車跟隨式(Two-predecessor follwing type,TPF)通信拓?fù)浣Y(jié)構(gòu)如圖2 所示.
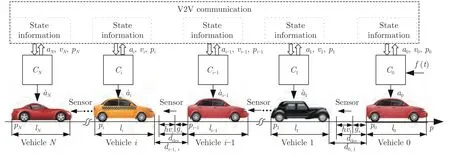
圖1 車輛隊(duì)列Fig.1 Vehicle platoon
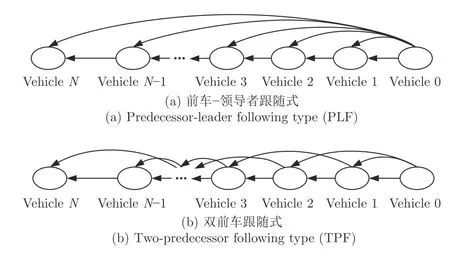
圖2 通信拓?fù)浣Y(jié)構(gòu)Fig.2 Communication topology
1.2 車輛模型建立
根據(jù)文獻(xiàn)[23],可建立車輛動(dòng)力學(xué)模型
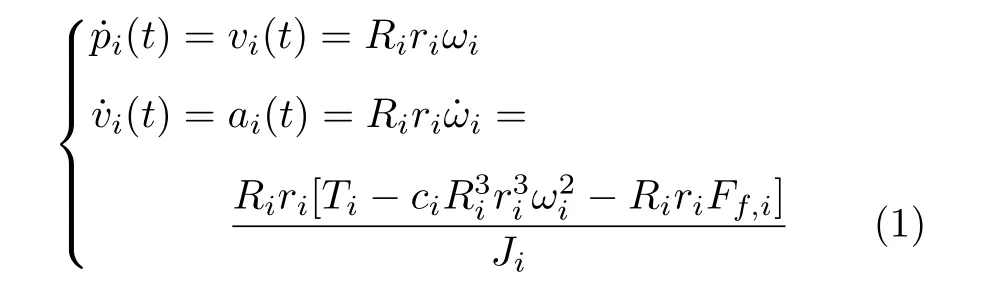
其中,ri是輪胎半徑,Ri是齒輪比,ωi是引擎轉(zhuǎn)速,Ti為引擎轉(zhuǎn)矩,ci為空氣阻尼系數(shù),Ff,i表示摩擦阻力,Ji為引擎轉(zhuǎn)動(dòng)慣量.
考慮車輛傳動(dòng)系統(tǒng)的遲滯特性,建立一階模型
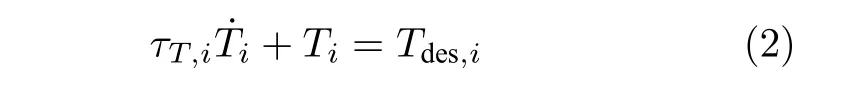
式中,τT,i為車輛動(dòng)力傳動(dòng)系統(tǒng)的時(shí)間常數(shù),Tdes,i為期望輸出力矩.
為了簡(jiǎn)化計(jì)算,設(shè)計(jì)線性反饋控制律
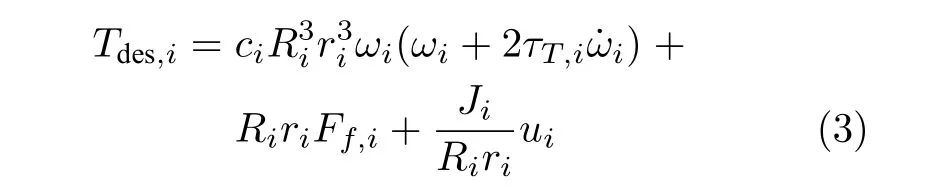
式中,ui為車輛的控制輸入.
由上述反饋線性化策略,可得到三階車輛動(dòng)力學(xué)模型
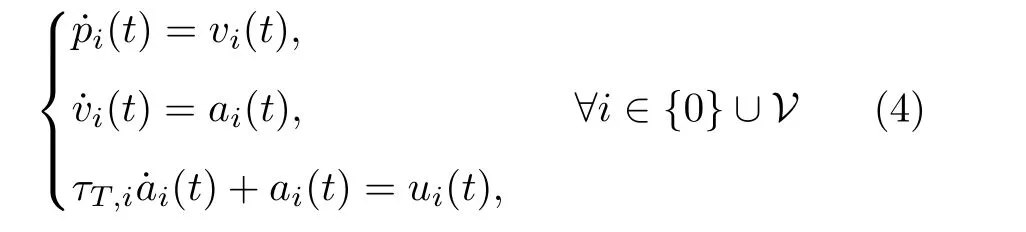
式中,pi(t),vi(t),ai(t)分別表示車輛i的位置,速度和加速度.ui(t)表示車輛i的控制輸入,τT,i刻畫了動(dòng)力傳動(dòng)系統(tǒng)的慣性時(shí)間,不同類型的車輛具有不同的慣性時(shí)間,其刻畫了車輛動(dòng)力學(xué)的異質(zhì)特性.
1.3 預(yù)備知識(shí)
引理 1[24].設(shè)三階系統(tǒng)的特征多項(xiàng)式為
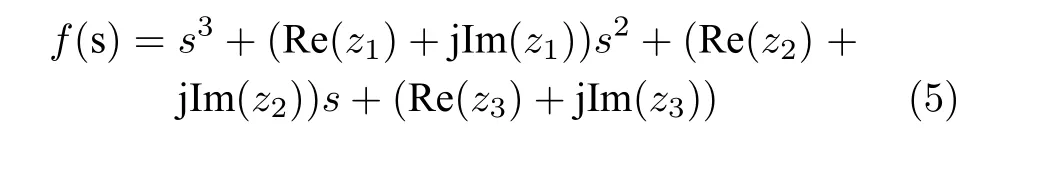
其中,z1,z2,z3為復(fù)數(shù),則系統(tǒng)矩陣Hurwitz 穩(wěn)定的必要條件為特征多項(xiàng)式(5)各項(xiàng)系數(shù)構(gòu)成的主行列式的各階主子式D1,D2,D3為正.
定義 1.集合C([a,b],Rn)是一個(gè)將區(qū)間[a,b]映射到 Rn的連續(xù)函數(shù)集合,對(duì)于函數(shù)φ ∈C([a,b],Rn)),定義連續(xù)范數(shù)‖·‖c:
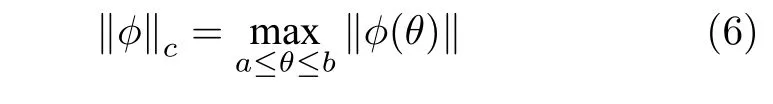
其中,向量范數(shù)‖·‖代表‖·‖2范數(shù).
令C([-δ,0],Rn)為定義在 [-δ,0] 上的連續(xù)函數(shù)的Banach 空間,φ∈C([-δ,0],Rn),那么有‖φ‖c=max-δ≤θ≤0‖φ(θ)‖.
考慮如下延時(shí)微分方程
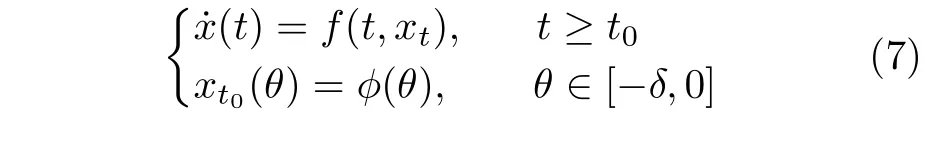
其中,δ>0,φ是初始條件的泛函,對(duì)于給定的t ≥t0,xt(·)表示將區(qū)間 [t-δ,t] 映射到 [-δ,0],也就是xt(θ)=x(t+θ),?θ ∈[-δ,0].
引理 2[25].假設(shè)f:R×C([-δ,0],Rn)→Rn是一個(gè) R×(C中的有界集)到 Rn中有界集的映射,并且u(s),v(s),w(s)是連續(xù)非減非負(fù)函數(shù),此外對(duì)于s/=0,u(s)和v(s)取正值,且u(0)=v(0)=0.如果存在連續(xù)可微泛函V:R×C →R,
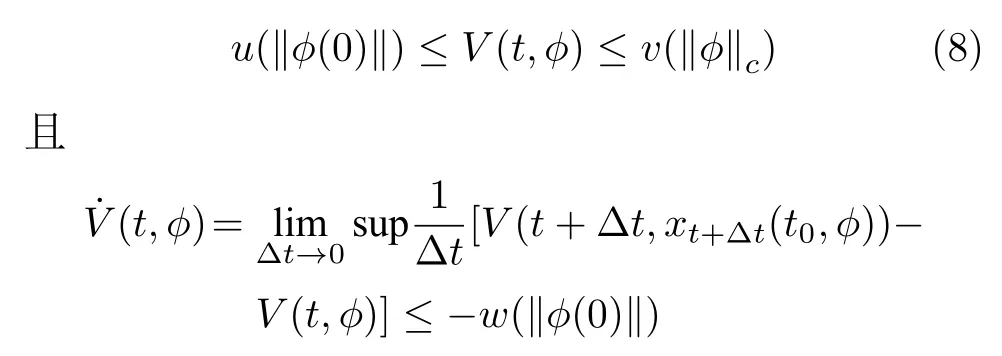
那么解x=0 是一致穩(wěn)定的.
此外,如果對(duì)于s>0,w(s)>0,那么系統(tǒng)是一致漸近穩(wěn)定的.如果
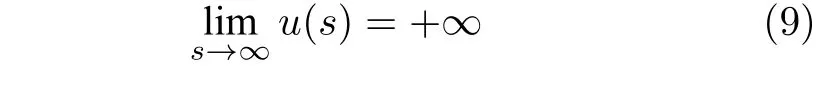
那么系統(tǒng)是全局一致漸近穩(wěn)定的.
1.4 控制目標(biāo)
車輛隊(duì)列控制旨在使隊(duì)列中所有車輛保持相同的速度和期望間距行駛,可以表示為
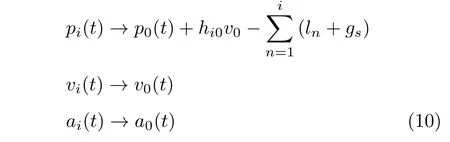
式中,l表示車身長(zhǎng)度,gs是相鄰兩車的安全距離.
假設(shè)領(lǐng)導(dǎo)車輛勻速運(yùn)動(dòng)(領(lǐng)導(dǎo)車輛的加速度視為擾動(dòng)),由此,可定義車輛位置、速度、加速度誤差為

根據(jù)式(11),車輛隊(duì)列控制目標(biāo)可改寫為
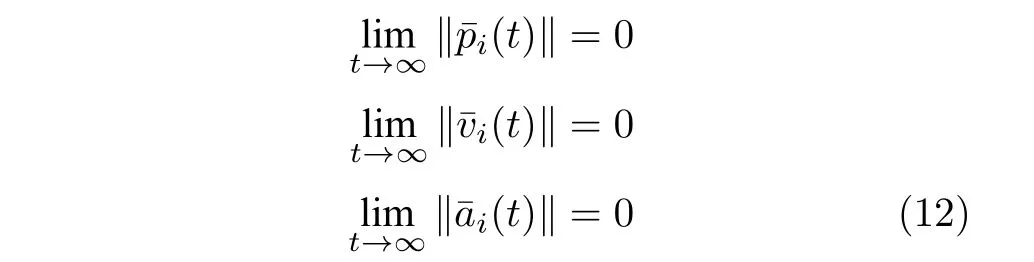
式中,(t),(t),(t)分別表示車輛i的位置、速度、加速度誤差.
2 控制器設(shè)計(jì)與穩(wěn)定性分析
2.1 控制器設(shè)計(jì)
針對(duì)上述車輛隊(duì)列控制問題,考慮車身長(zhǎng)度的異質(zhì)性、車輛位置一致性、速度一致性以及車輛跟馳行為特性,設(shè)計(jì)分布式控制器:

在式(13)中,ki,w>0,ki,p>0,ki,v>0,k0,p>0,k0,v>0是反饋控制增益.aij∈{0,1}和ρi0∈{0,1}分別是跟隨車輛i與車輛j,跟隨車輛i與領(lǐng)導(dǎo)車輛之間的通信連接.hij和hi0分別是跟隨車輛i與車輛j,跟隨車輛i與領(lǐng)導(dǎo)車輛之間的間距常數(shù).ln是第n(n=1,···,i)輛車的長(zhǎng)度.gs是相鄰車輛的安全距離.τij(t)與τi0(t)分別為跟隨車輛i與車輛j,跟隨車輛i與領(lǐng)導(dǎo)車輛之間的通信延時(shí).車輛跟馳行為采用最優(yōu)速度進(jìn)行刻畫[26]:

2.2 穩(wěn)定性分析
針對(duì)通過V2X 通信獲取其他車輛狀態(tài)信息存在通信延時(shí)的情況,本文設(shè)計(jì)了考慮存在通信延時(shí)的控制器(13).可將該車輛隊(duì)列系統(tǒng)視為一個(gè)延時(shí)系統(tǒng),其穩(wěn)定性可采用引理2 (Lyapunov-Krasovskii 定理)描述的延時(shí)系統(tǒng)穩(wěn)定性證明方法,構(gòu)造Lyapunov-Krasovskii 泛函加以證明,其詳細(xì)證明過程如下.首先根據(jù)狀態(tài)方程(4)和誤差定義(11),跟隨車輛與領(lǐng)導(dǎo)車輛間的距離時(shí)間常數(shù)關(guān)系hi0-hj0=hij=-hji,可得誤差狀態(tài)方程:

基于式(14),利用泰勒公式線性化可得
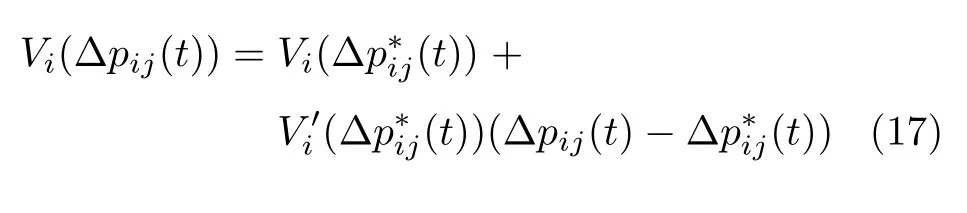

注 2.此部分內(nèi)容主要為誤差狀態(tài)方程的線性化.由于考慮車輛跟馳行為特性,在控制器中引入了非線性項(xiàng)(14),為此,根據(jù)誤差定義(11)變換狀態(tài)方程(4)為誤差狀態(tài)方程(15),并采用泰勒公式獲得線性化的誤差狀態(tài)方程(19),從而簡(jiǎn)化后續(xù)穩(wěn)定性分析過程.

根據(jù)上述定義,車輛隊(duì)列系統(tǒng)的誤差狀態(tài)空間表達(dá)式可以用以下延時(shí)微分方程表示為
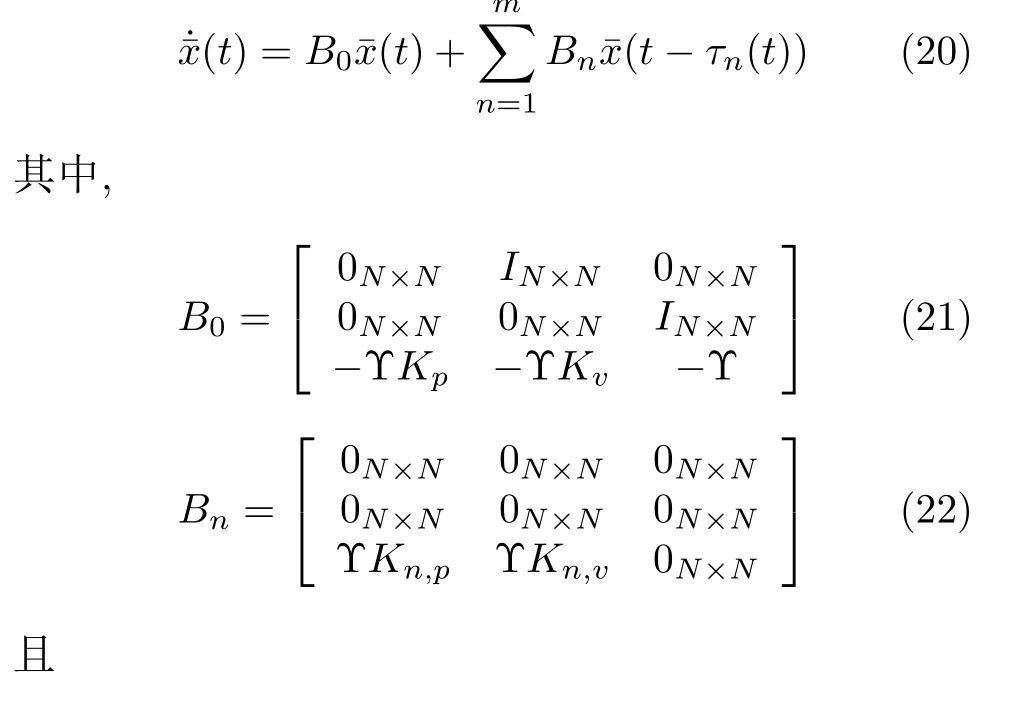
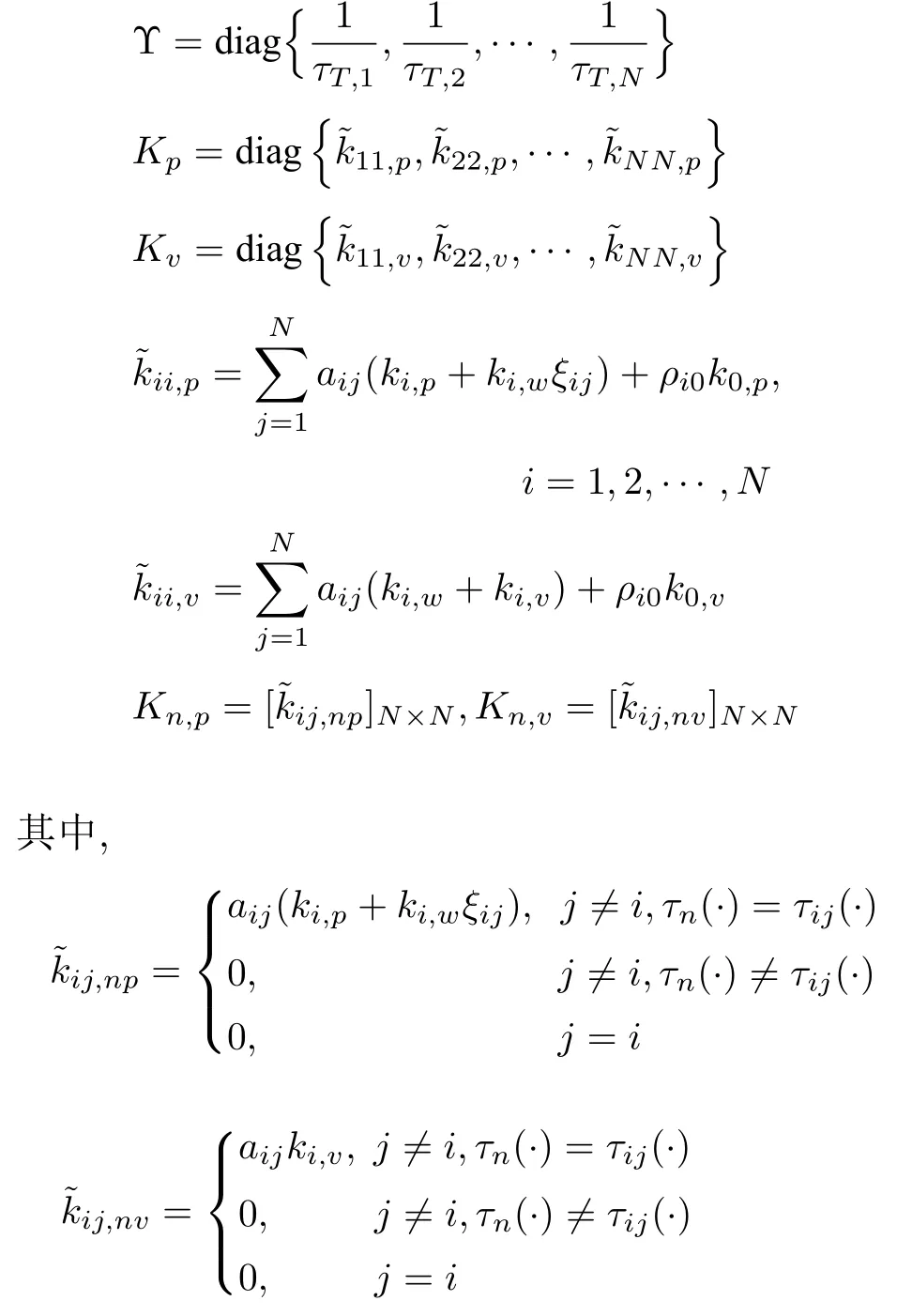
根據(jù)牛頓-萊布尼茲公式可得
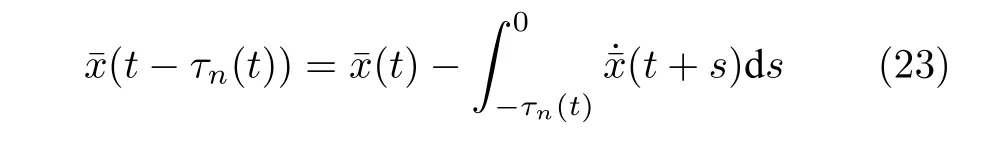
因此,將式(20)代入式(23),可得
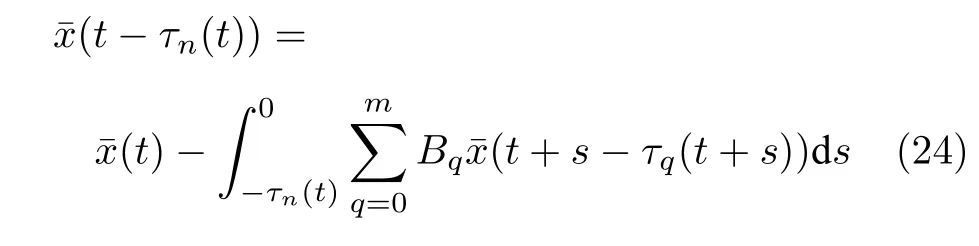
式中,B0,···,Bm由式(21)和式(22)表示,且τ0(t)≡0.
將式(24)代入時(shí)變系統(tǒng)(20)可以得到
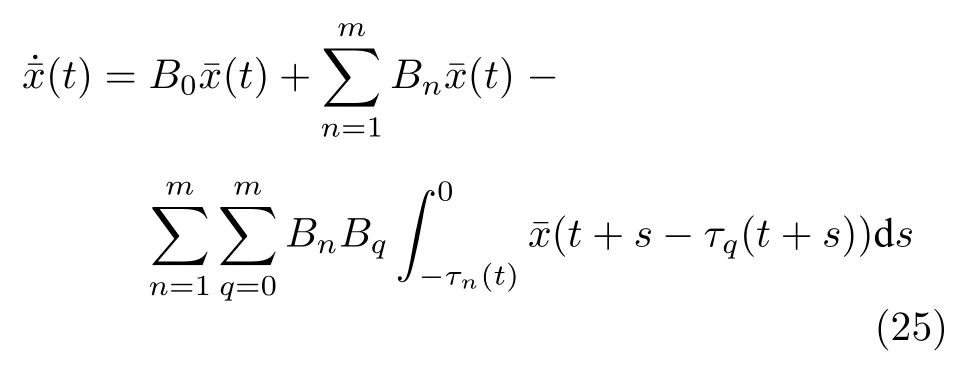
根據(jù)式(21)和式(22),可以得到BnBq=0,n=1,···,m,q=1,···,m(q/=0).因此系統(tǒng)(19)可以定義為
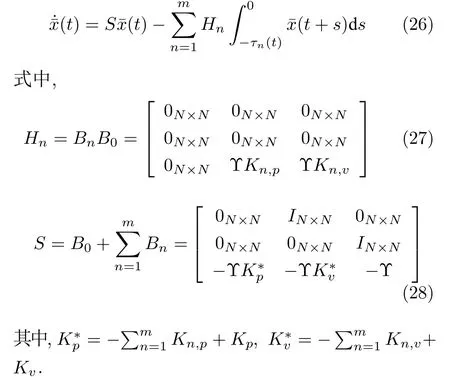
注 3.此部分內(nèi)容主要為誤差狀態(tài)方程的積分變換.利用牛頓-萊布尼茲公式,對(duì)誤差狀態(tài)方程(20)做積分變換得到式(26),為利用Hadamard 不等式縮放Lyapunov-Krasovskii 泛函,分析系統(tǒng)穩(wěn)定性.
定理1.考慮延時(shí)系統(tǒng)(26),設(shè)置控制參數(shù)ki,w,ki,p和ki,v為正.假設(shè)延時(shí)τn(t)(n=1,···,m)是有界的,即τn(t)∈[0,τmax],(t)∈(-∞,rn](?t?n)且rn≤1.那么存在常數(shù)τ*>0,對(duì)于τn(t)<τ*,?n?t有
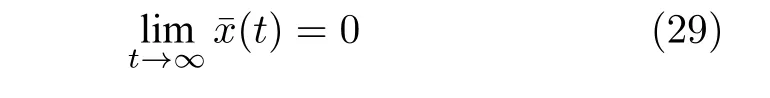
當(dāng)且僅當(dāng)矩陣S是Hurwitz 穩(wěn)定.
證明.(充分性):考慮系統(tǒng)(26)的Lyapunov-Krasovskii 泛函:
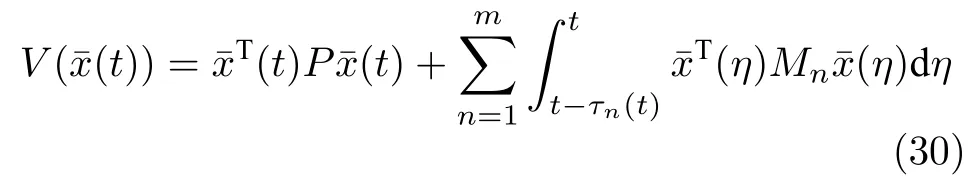
其中,選取矩陣P=PT>0且Mn>0(n=1,···,m),并定義如下連續(xù)非減的正值函數(shù):
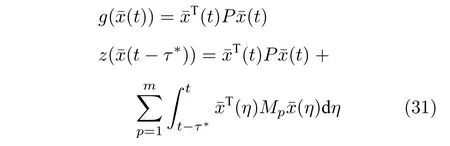
其中,τ*是可能的最大延時(shí).
根據(jù)式(30)和式(31),引理2 的條件(8)可以滿足,即
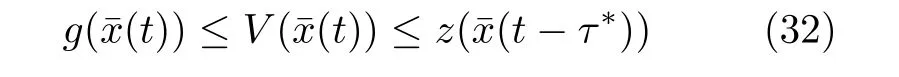
對(duì)式(30)求導(dǎo)可得
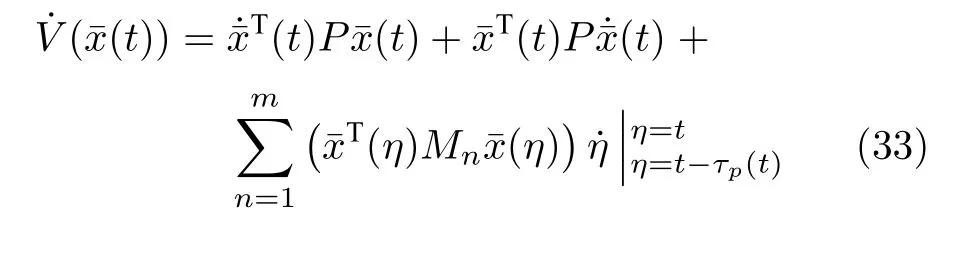
將式(26)代入式(33),可得
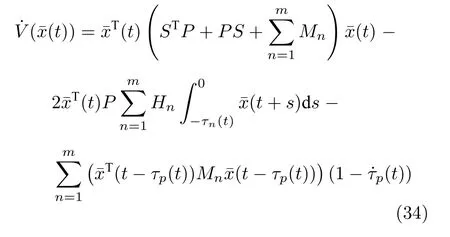
根據(jù)附錄A,設(shè)置參數(shù)ki,w,ki,p和ki,v,使得矩陣S是Hurwitz 穩(wěn)定的.且根據(jù)Lyapunov 理論,令STP+PS=-Q,其中,P,Q是正定的,P=PT.
對(duì)于任意的正定矩陣 Ξ,有[27]
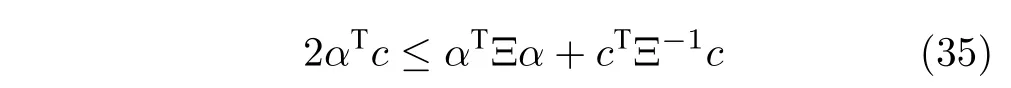
因此,令αT=TSHn,c=(t+s),Ξ=S-1,那么
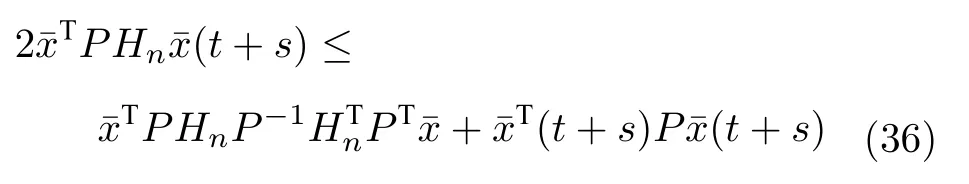
根據(jù)式(36),式(34)可以改寫為
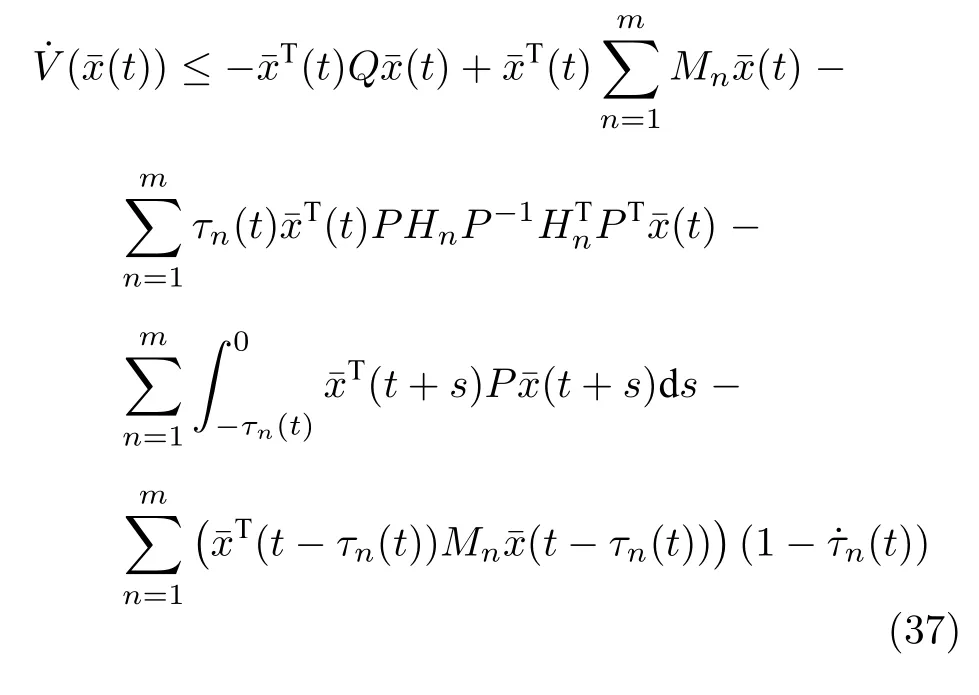
根據(jù)Hadamard 不等式[28],有
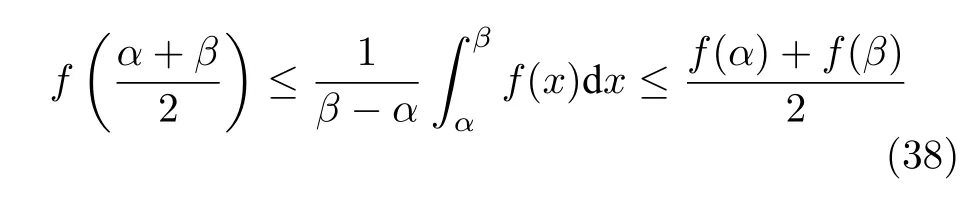
可以將式(37)的積分部分進(jìn)一步縮放,以及代入延時(shí)邊界可得
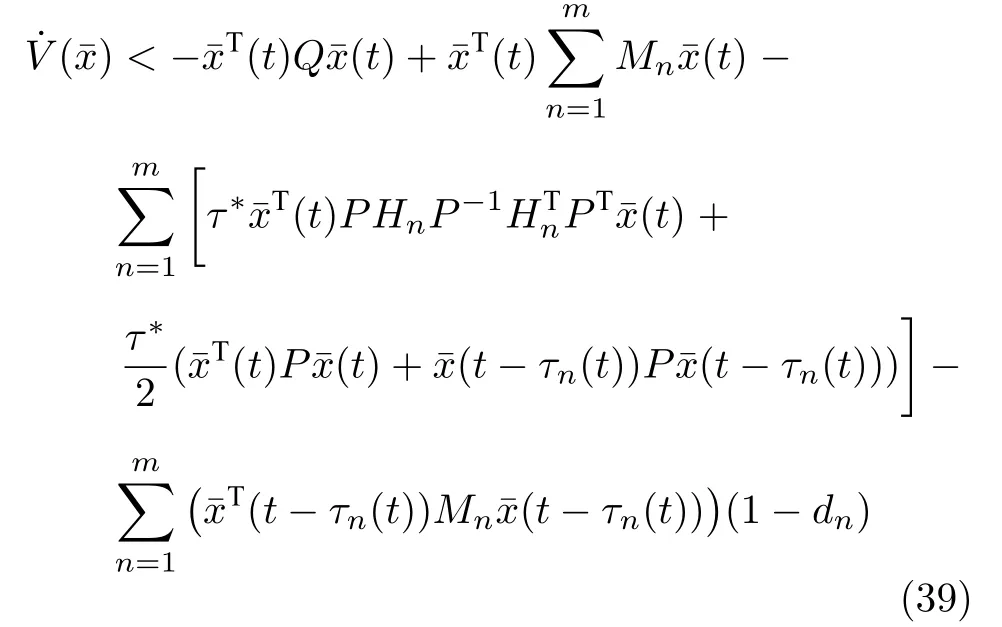
定義一個(gè)新的誤差狀態(tài)向量ε(t)=[(t),xˉ(tτ1)(t-τm(t))]T,將式(39)重寫為一個(gè)更簡(jiǎn)潔的形式

根據(jù)引理2 可得,保證延時(shí)系統(tǒng)一致漸近穩(wěn)定的充分條件為 Λ 負(fù)定.由于rn≤1,?n=1,···,m,因此n=2,···,m時(shí) Λn負(fù)定.因此,當(dāng) Λ1負(fù)定時(shí),Λ是負(fù)定的.即

注 4.此部分內(nèi)容主要為基于引理2 的系統(tǒng)穩(wěn)定性分析.基于引理2,通過構(gòu)造Lyapunov-Krasovskii 泛函(30),且滿足引理1 的條件(8),進(jìn)一步根據(jù)Lyapunov 理論和Hadamard 不等式得到系統(tǒng)的延時(shí)上界條件.
2.3 弦穩(wěn)定性分析
定義2.如果車輛隊(duì)列系統(tǒng)中相鄰兩車的間距誤差有如下關(guān)系:
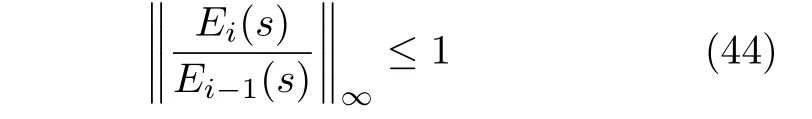
其中,Ei(s)是i車與i-1 車的間距誤差,則稱車輛隊(duì)列系統(tǒng)滿足弦穩(wěn)定性(String stability)[29].
將車輛動(dòng)力學(xué)模型(4)和控制器(13)進(jìn)行拉普拉斯變換,同時(shí)考慮最差情形(通信延時(shí)最大),即選取τ*作為系統(tǒng)的通信延時(shí),經(jīng)過分析可得
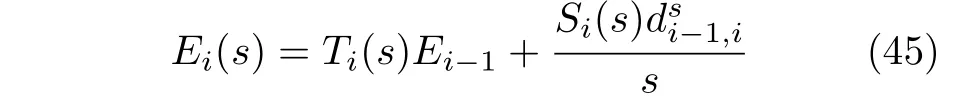
其中,Ti(s)和Si(s)的表達(dá)式及詳細(xì)推導(dǎo)過程見附錄B,控制增益的選取滿足Ti(jω)<1.
3 仿真驗(yàn)證
本節(jié)將所提控制器(13)與文獻(xiàn)[16]控制器分別在PLF 和TPF 通信拓?fù)浣Y(jié)構(gòu)且考慮無(wú)通信延時(shí)和存在最大0.03 s 延時(shí)情況下進(jìn)行對(duì)比仿真實(shí)驗(yàn),驗(yàn)證了所提控制器的有效性和通信時(shí)延情況下的優(yōu)越性.首先選取N=8 輛車(1 輛領(lǐng)導(dǎo)車輛和7 輛跟隨車輛)作為實(shí)驗(yàn)對(duì)象.車輛長(zhǎng)度選取為一般的乘用車長(zhǎng)度li=4+lrm,其中,lr∈[0,1].在保證無(wú)碰撞風(fēng)險(xiǎn)的情形下,領(lǐng)導(dǎo)車輛的初始位置設(shè)定為p0(0)=150m,跟隨車輛的初始位置p(0)=[126,105,83,64,43,22,1]m.領(lǐng)導(dǎo)車輛的速度如式(46)所示:
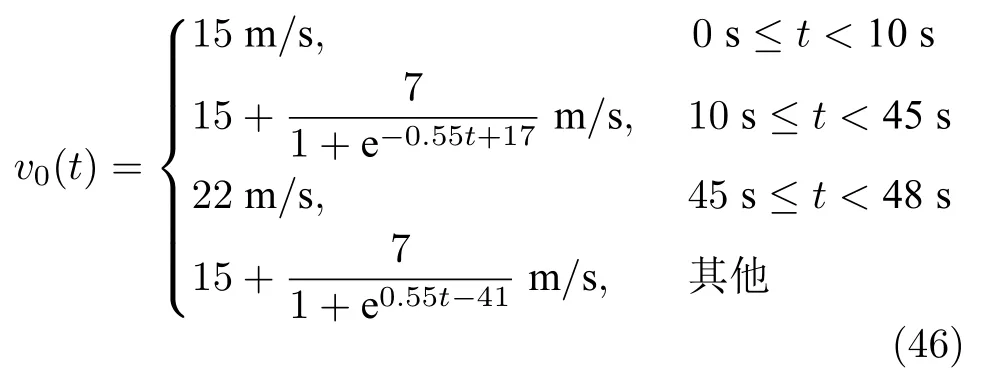
跟隨車輛的初始速度和加速度分別為vi(0)=v0(0)m/s,ai(0)=0 m/s2,i=1,2,···,N.時(shí)變延時(shí) 0<τ(t)<τ*=10.32×10-2s,其中,τ*大于典型的IEEE802.11p 車聯(lián)網(wǎng)通信延時(shí)[30].控制器參數(shù)及車輛結(jié)構(gòu)參數(shù)如表1 所示.

表1 控制器參數(shù)Table 1 Controller parameters
3.1 PLF通信拓?fù)浣Y(jié)構(gòu)下的仿真分析
領(lǐng)導(dǎo)車輛按照式(46)所給速度行駛,跟隨車輛初始時(shí)刻速度與領(lǐng)導(dǎo)車輛相同,在無(wú)通信延時(shí)和最大0.03 s 延時(shí)情況下,文獻(xiàn)[16]的控制器和本文所提控制器(13)作用下的位置、速度、加速度和間距誤差軌跡如圖3~6 所示,所有仿真圖中的v0,v1,···,v7分別表示Vehicle 0,Vehicle 1,···,Vehicle 7.圖3 為車輛的位置軌跡.由圖3(a)以及圖3(b)~3(d)得出,在有/無(wú)通信延時(shí)和文獻(xiàn)[16]的控制器及本文所提控制器(13)的作用下,隊(duì)列內(nèi)的所有車輛能夠保持穩(wěn)定的間距行駛,并在領(lǐng)導(dǎo)車輛加速和減速后隊(duì)列仍能保持穩(wěn)定和期望的安全間距.
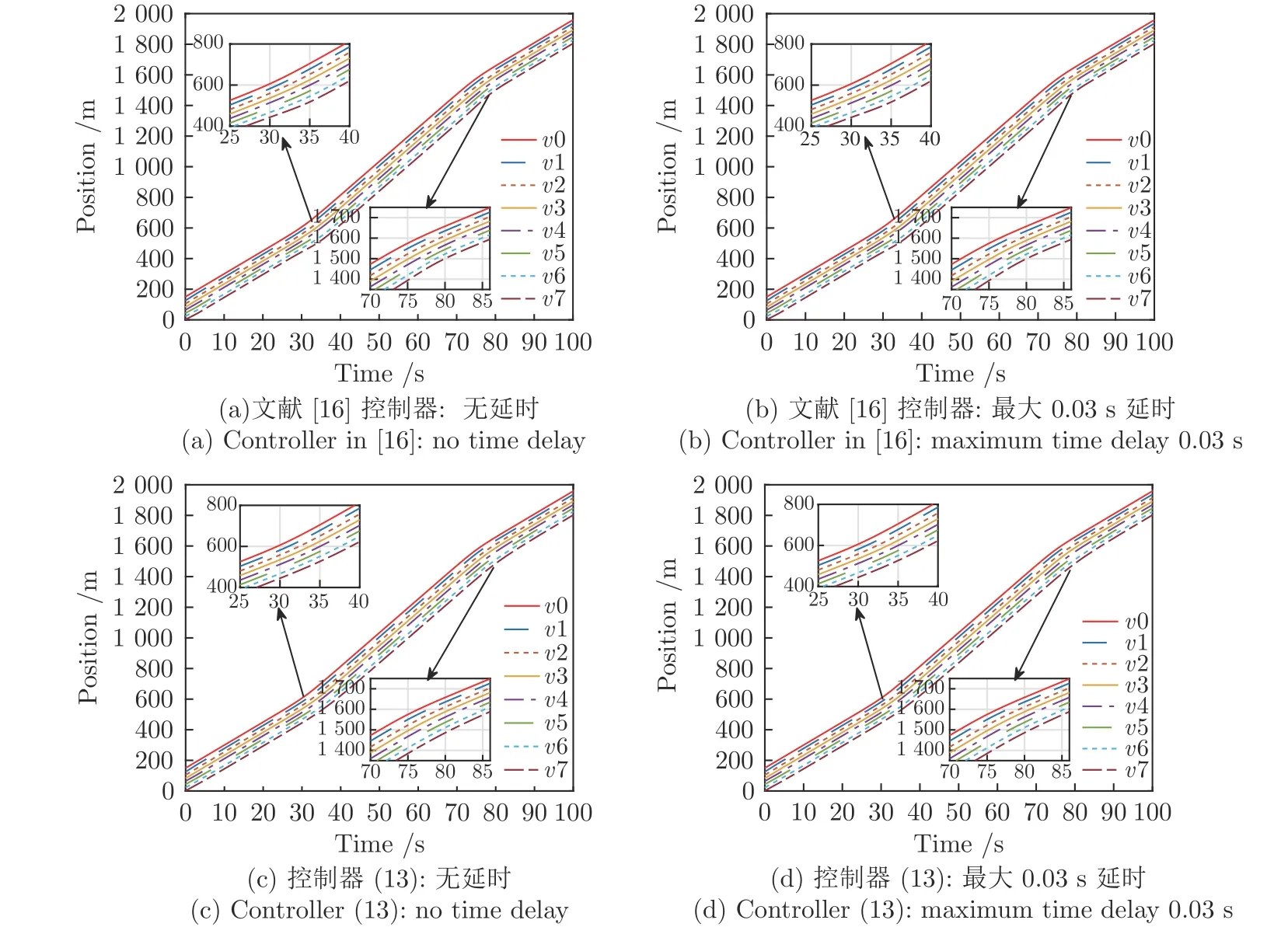
圖3 PLF 拓?fù)湎萝囕v隊(duì)列的位置圖Fig.3 Position profile for a platoon under PLF topology
圖4 是隊(duì)列內(nèi)所有車輛的速度圖.基于圖4,領(lǐng)導(dǎo)者具有時(shí)變速度,可以分為3 個(gè)階段:加速、勻速和減速.在文獻(xiàn)[16] 的控制器及本文所提控制器(13)作用下,跟隨車輛的速度最終可收斂到與領(lǐng)導(dǎo)車輛速度一致.圖4(b)和4(d)表明存在通信延時(shí)情況時(shí),文獻(xiàn)[16] 的控制器由于未考慮通信延時(shí)的間距補(bǔ)償,故在速度收斂后仍產(chǎn)生波動(dòng),且通信延時(shí)越大,產(chǎn)生的波動(dòng)幅值也越大,從而導(dǎo)致車輛隊(duì)列的不穩(wěn)定行駛.而本文所提控制器考慮了通信延時(shí)的間距補(bǔ)償,緩解了由通信延時(shí)產(chǎn)生的車輛速度波動(dòng).
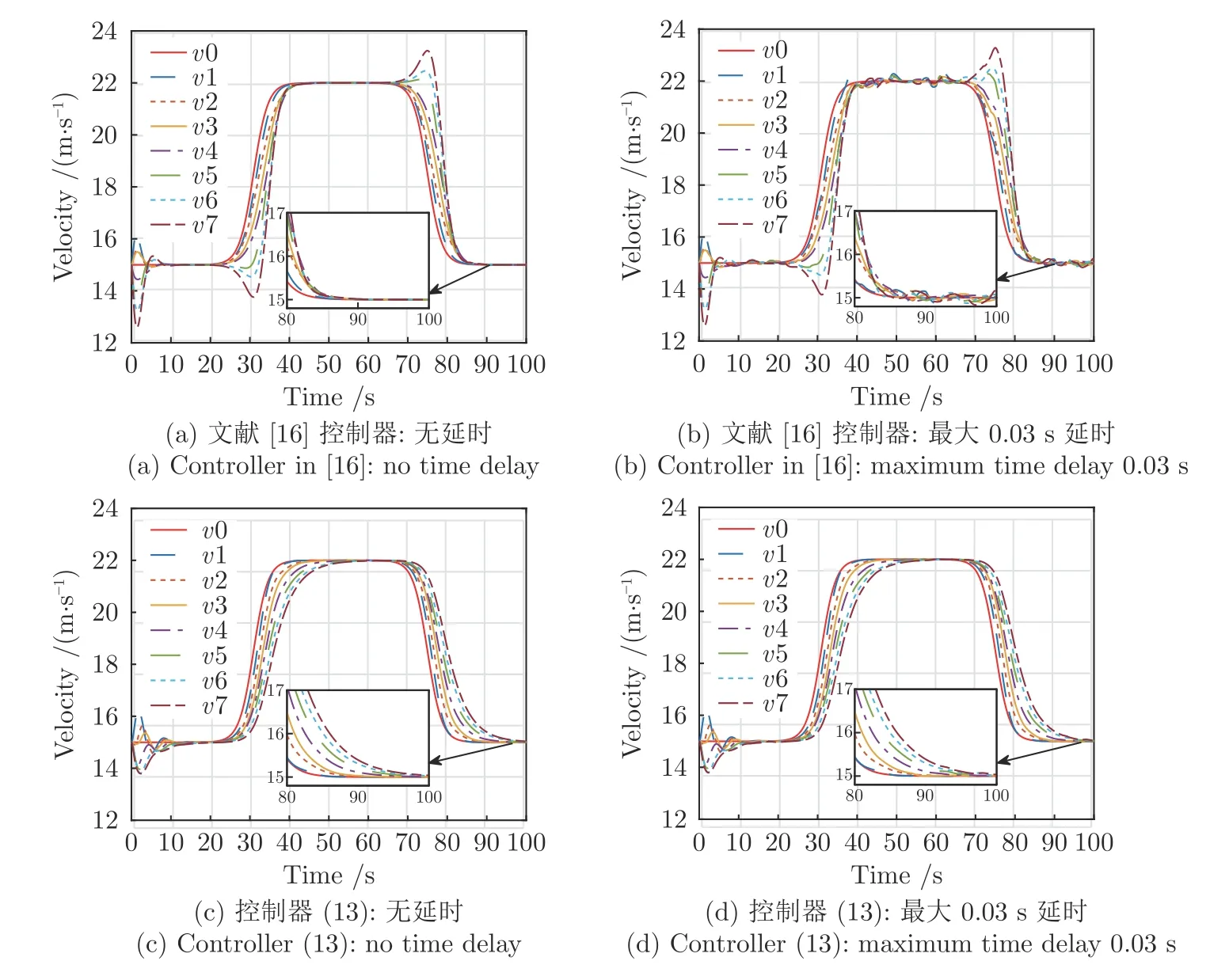
圖4 PLF 拓?fù)湎萝囕v隊(duì)列的速度圖Fig.4 Velocity profile for a platoon under PLF topology
圖5 是加速度圖.由圖5(a)和5(b)可知,在加速階段,文獻(xiàn)[16]的控制器作用下跟隨車輛最大加速度振幅為1.7 m/s2,且跟隨車輛加速度更易受到通信延時(shí)的影響,最大通信延時(shí)0.03s 的情形下,加速度波動(dòng)幅度最大約0.5m/s2.而圖5(c)和5(d)表明本文所提控制器作用下跟隨車輛最大加速度振幅為1.0 m/s2,在最大通信延時(shí)0.03 s 的情形下,跟隨車輛加速度幾乎不受影響.因此所提控制器能更好地保證車輛加速度的平穩(wěn)性和抑制通信延時(shí)的干擾.

圖5 PLF 拓?fù)湎萝囕v隊(duì)列的加速度圖Fig.5 Acceleration profile for a platoon under PLF topology
圖6 是間距誤差圖.由圖6(a)和6(b)可知,跟隨車輛的位置間距誤差最終收斂到一致,表明在文獻(xiàn)[16]的控制器作用下,車輛能夠以隊(duì)列模式行駛,但容易受到通信延時(shí)的影響,從而導(dǎo)致車輛隊(duì)列間距的波動(dòng).圖6(c)和6(d)表明在本文所提控制器作用下不僅間距誤差能夠收斂到一致,而且能夠很好抑制通信延時(shí)的影響.此外,領(lǐng)導(dǎo)車輛減速過程中間距誤差始終為正,且沒有負(fù)的超調(diào),表明所提控制器能夠保證車輛隊(duì)列行駛的安全性.因?yàn)楸疚脑谠O(shè)計(jì)控制器時(shí)考慮了車輛跟馳作用.
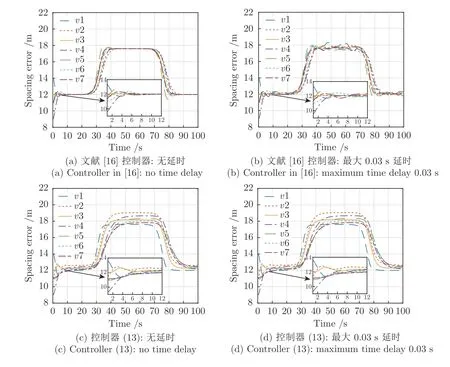
圖6 PLF 拓?fù)湎萝囕v隊(duì)列的間距誤差圖Fig.6 Spacing error profile for a platoon under PLF topology
3.2 TPF通信拓?fù)浣Y(jié)構(gòu)下的仿真分析
考慮TPF 通信拓?fù)浣Y(jié)構(gòu),在無(wú)通信延時(shí)和最大0.03 s 通信延時(shí)情況下,文獻(xiàn)[16]的控制器和本文所提控制器(13)作用下的位置、速度、加速度和間距誤差軌跡如圖7~10 所示.圖7 是位置圖.由圖7(a)和7(b)~7(d)可知,在TPF 通信拓?fù)浣Y(jié)構(gòu)下,文獻(xiàn)[16]的控制器和本文所提控制器仍能在無(wú)通信延時(shí)和最大0.03 s 通信延時(shí)情形下,使領(lǐng)導(dǎo)車輛和跟隨車輛保持相同間距行駛.

圖7 TPF 拓?fù)湎萝囕v隊(duì)列的位置軌跡圖Fig.7 Position trajectory profile for a platoon under TPF topology
圖8 給出了所有車輛的速度曲線.根據(jù)圖8 可知,領(lǐng)導(dǎo)車輛的運(yùn)動(dòng)狀態(tài)可分為加速、勻速和減速三個(gè)階段,最終跟隨車輛的速度都收斂到與領(lǐng)導(dǎo)車輛一致.進(jìn)一步由圖8(a)和8(b)可知,在文獻(xiàn)[16]的控制器作用下通信延時(shí)使跟隨車輛的速度產(chǎn)生波動(dòng),最大波動(dòng)約為0.2 m/s,且相對(duì)于PLF 通信拓?fù)浣Y(jié)構(gòu)下的波動(dòng)更顯著.由圖8(c)和8(d)可知,本文所提控制器由于考慮通信延時(shí)的間距補(bǔ)償,能夠很好適應(yīng)通信延時(shí)帶來的擾動(dòng),且相對(duì)于PLF 通信拓?fù)?在領(lǐng)導(dǎo)車輛速度改變時(shí)跟隨車輛速度有更劇烈的變化.
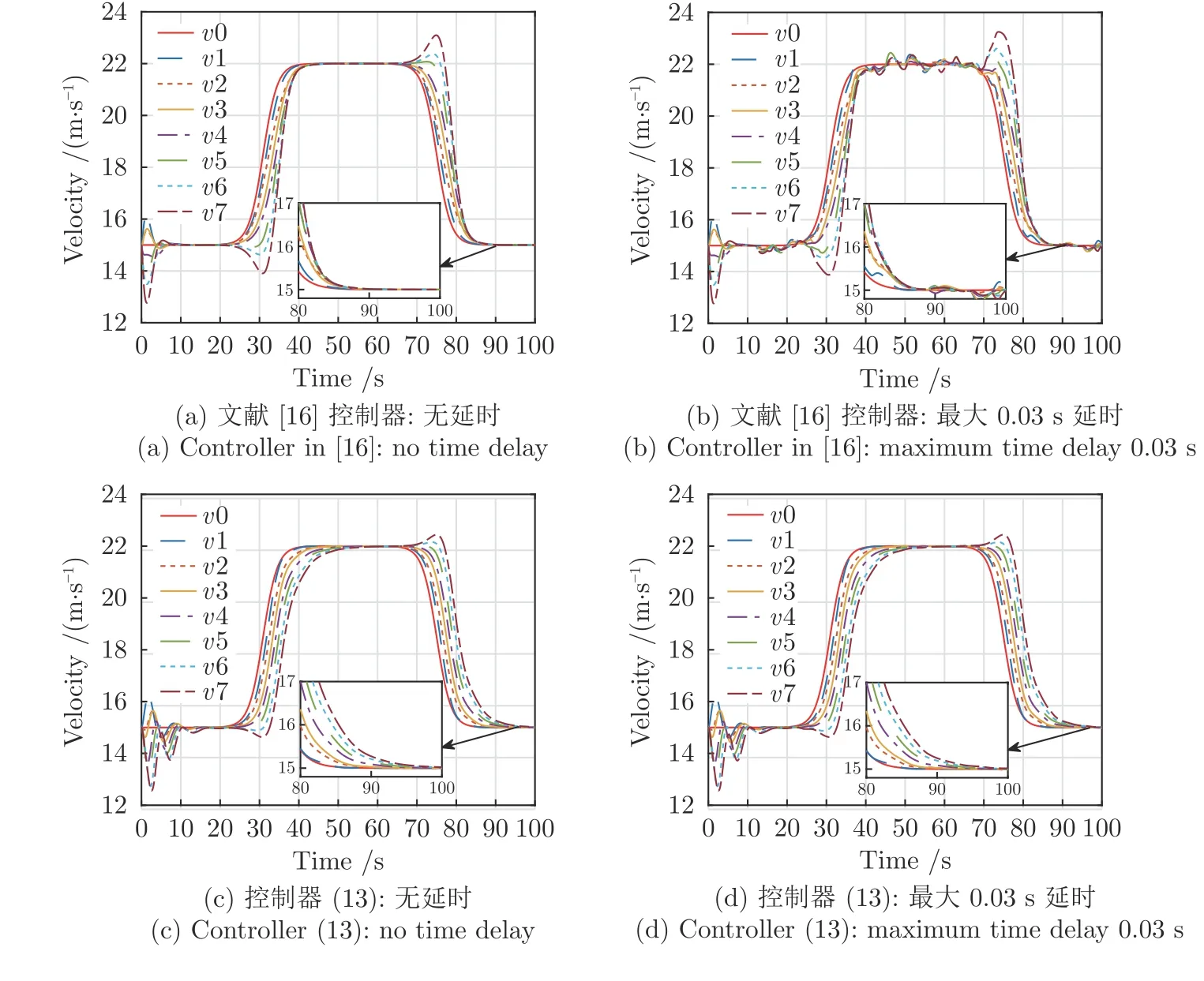
圖8 TPF 拓?fù)湎萝囕v隊(duì)列的速度圖Fig.8 Velocity profile for a platoon under TPF topology
圖9 是加速度圖.根據(jù)圖9 可知,跟隨車輛的加速度在領(lǐng)導(dǎo)車輛經(jīng)過加速和減速階段后仍能與領(lǐng)導(dǎo)和車輛保持一致.由圖9(a)和9(b)可知,在文獻(xiàn)[16]的控制器作用下,跟隨車輛的加速度受通信延時(shí)的影響較大,最大波動(dòng)約0.6m/s2,且比PLF通信拓?fù)浣Y(jié)構(gòu)下更顯著.圖9(c)和9(d)說明,本文所提控制器能夠使跟隨車輛的加速度在通信延時(shí)的影響下仍保持平滑,因此可保證更好的乘坐舒適性,且相比TPF 通信拓?fù)?跟隨車輛加速度的幅值會(huì)隨著車輛編號(hào)的增大而略微增大,這與文獻(xiàn)[10]中描述的車輛隊(duì)列的穩(wěn)定性與領(lǐng)導(dǎo)車輛和跟隨車輛的通信連接關(guān)系緊密的結(jié)論相吻合.
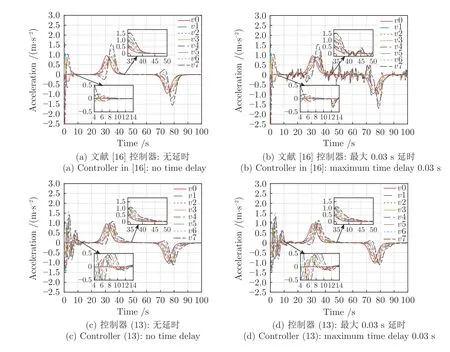
圖9 TPF 拓?fù)湎萝囕v隊(duì)列的加速度圖Fig.9 Acceleration profile for a platoon under TPF topology
圖10 是間距誤差圖.根據(jù)圖10 可知,跟隨車輛能與領(lǐng)導(dǎo)車輛能夠保持穩(wěn)定的隊(duì)列行駛.圖10(a)和10(b)表明在文獻(xiàn)[16]的控制作用下通信延時(shí)會(huì)造成跟隨車輛間距誤差的波動(dòng).且在領(lǐng)導(dǎo)車輛速度發(fā)生變化時(shí),跟隨車輛的誤差間距會(huì)產(chǎn)生超調(diào),因此在與前車距離較近時(shí)可能導(dǎo)致碰撞風(fēng)險(xiǎn).而在本文所提控制器的作用下通信延時(shí)對(duì)于誤差間距的影響較小,且在領(lǐng)導(dǎo)車輛速度發(fā)生變化時(shí),跟隨車輛的間距誤差沒有產(chǎn)生超調(diào),可以避免碰撞風(fēng)險(xiǎn).
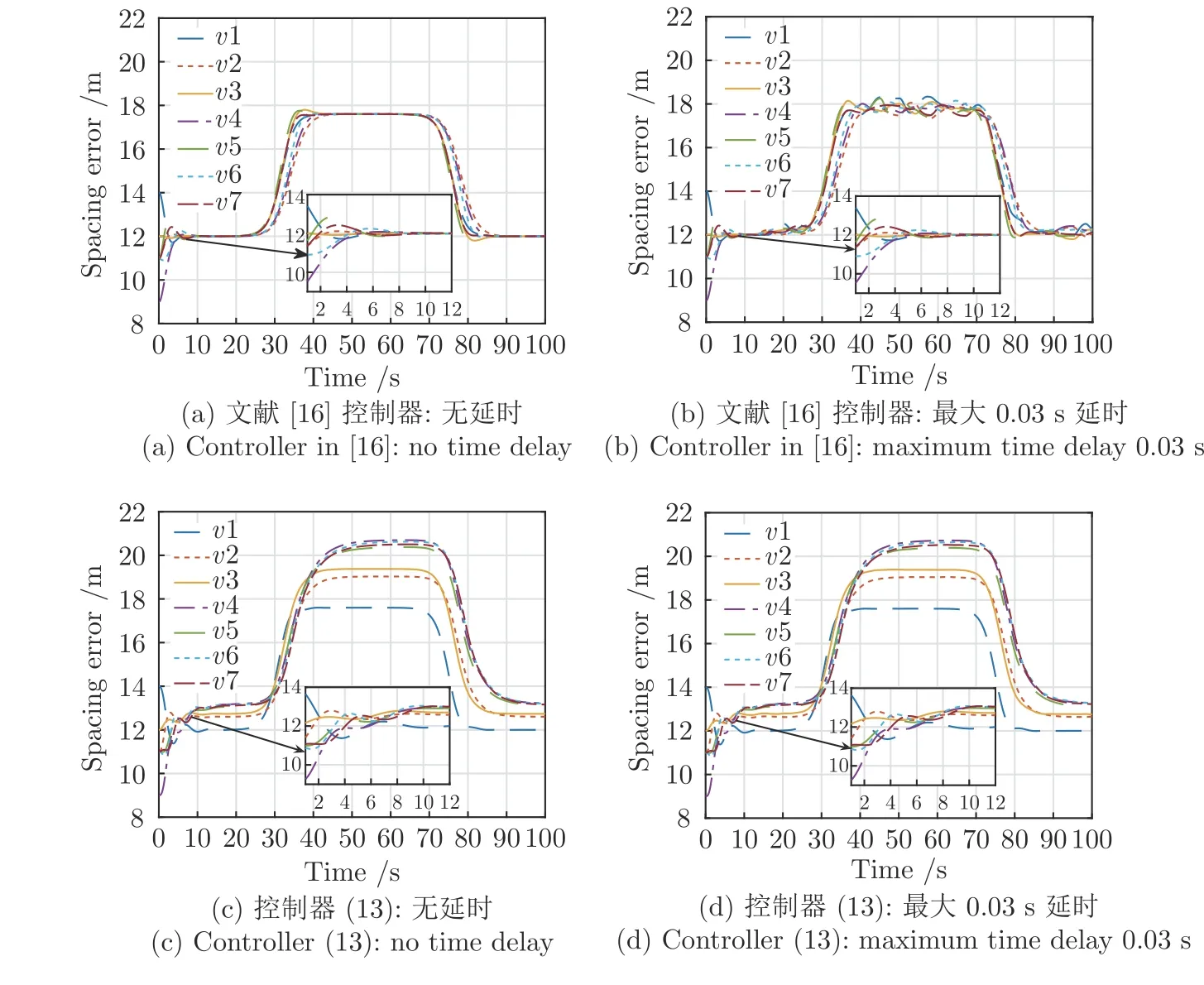
圖10 TPF 拓?fù)湎萝囕v隊(duì)列的間距誤差圖Fig.10 Spacing error profile for a platoon under TPF topology
4 結(jié)論
本文考慮車輛間的非線性作用和通信延時(shí)的影響基于車輛三階動(dòng)力學(xué)模型提出一種分布式異質(zhì)車輛隊(duì)列非線性縱向控制器.保證車輛在通信延時(shí)的影響下仍能以隊(duì)列模式行駛并且避免了負(fù)誤差間距的產(chǎn)生,即滿足車輛行駛的安全性.然后,通過Lyapunov-Krasovskii 定理證明了所提控制器的穩(wěn)定性,并得出通信延時(shí)上界.最后,考慮無(wú)通信延時(shí)和最大0.03 s 通信延時(shí)兩種場(chǎng)景,通過數(shù)值仿真對(duì)比驗(yàn)證了文獻(xiàn)[16]的控制器與本文所提控制器在TPL 和PLF 通信拓?fù)浣Y(jié)構(gòu)下的控制效果,并得出由于考慮間距補(bǔ)償和車輛跟馳行為特性,本文所提控制器在兩種通信拓?fù)浣Y(jié)構(gòu)下均能更好地抑制通信延時(shí)帶來的波動(dòng)和避免碰撞風(fēng)險(xiǎn).
附錄A
矩陣S的Hurwitz 穩(wěn)定條件分析:令λ為矩陣S的特征根,則有
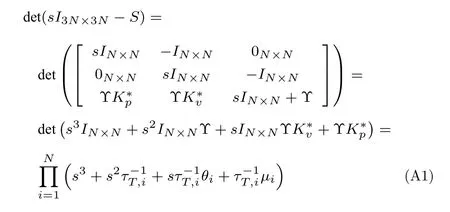
根據(jù)引理1,其各階主子式D1,D2,D3為
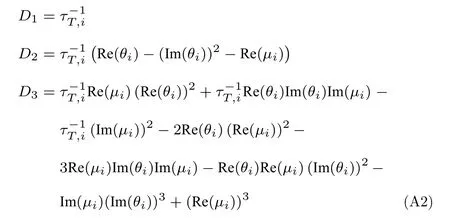
其中,θi是的第i個(gè)特征值,μi是的第i個(gè)特征值.
因此,根據(jù)引理1,可得矩陣S是Hurwitz 穩(wěn)定的條件為ki,w>0,ki,p>0,ki,v>0,且D1,D2,D3均為正.
附錄B
根據(jù)車輛動(dòng)力學(xué)模型(4)可得
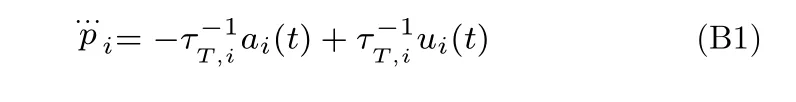
對(duì)式(B1)進(jìn)行Laplace 變換L(·)

當(dāng)i=2,···,N時(shí),
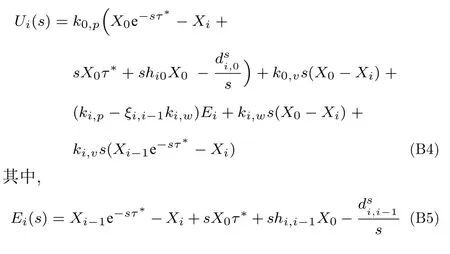
將式(B4)代入式(B2)可得:
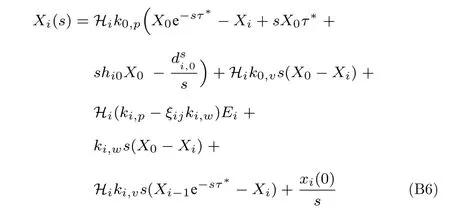
當(dāng)i=1 時(shí),
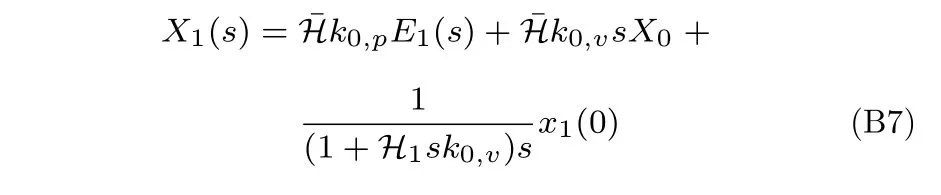
其中,
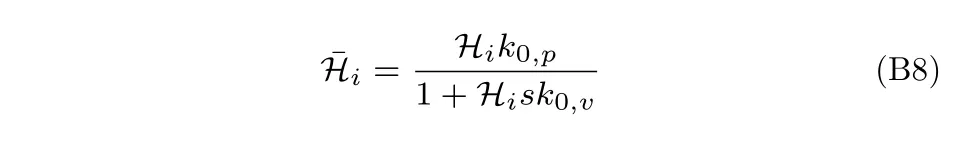
于是將式(B7)代入式(B5)可得:

假設(shè)車輛隊(duì)列滿足穩(wěn)定性,那么可以得到h2,0=h2,1+,于是由式(B13)可得
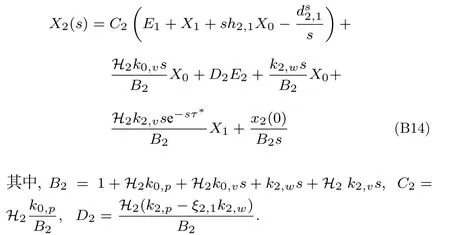
將式(B14)兩邊同時(shí)減去X1e-τ*s,且根據(jù)式(B5),可將式(B14)改寫為
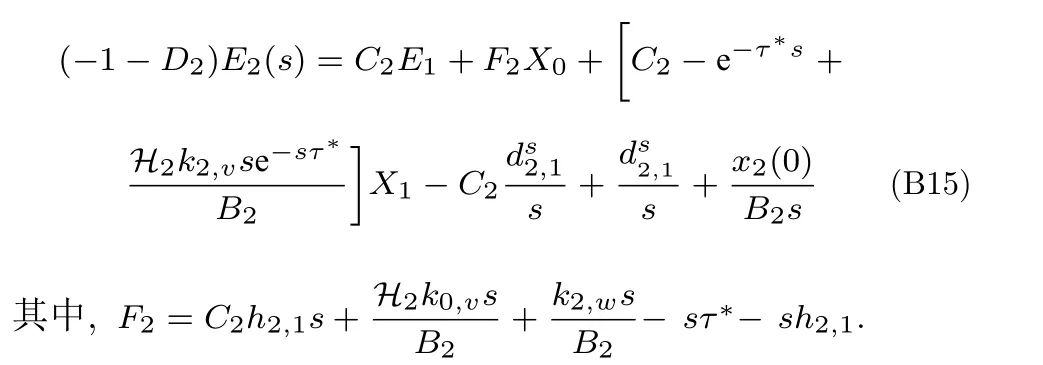
根據(jù)式(B7)和式(B9),分別將X1和X0代入式(B15)中可得:
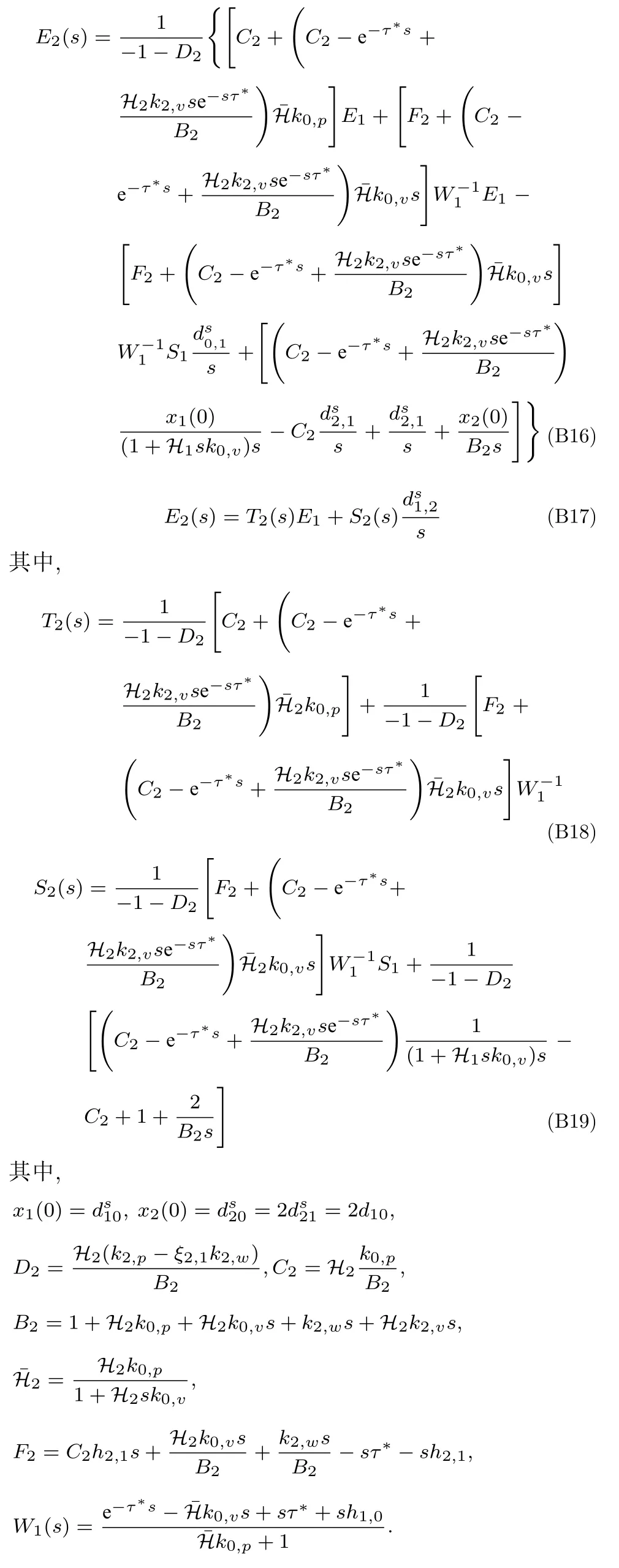
同理推廣可得:
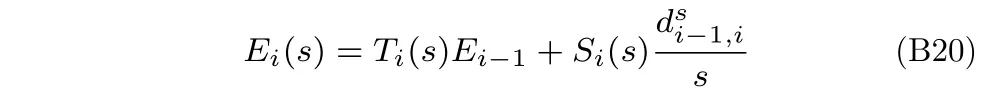
其中,


