一類非線性系統模糊自適應固定時間量化反饋控制

王煥清 陳 明 劉曉平

量化控制問題一直以來受到很多學者的廣泛關注,作為網絡控制中不可或缺的重要環節,旨在通過量化器把連續信號轉換為在有限集中取值的分段信號.尤其隨著數字設備性能的提高及網絡化系統的應用和發展,量化控制已然成為解決網絡化控制問題最有效的方法之一.

近年來,非線性系統的量化控制問題成為了一個新的研究熱點[1].文獻[2]針對一類非線性系統,提出了一種對數量化反饋控制器設計方法.文獻[3]探討了一類非線性離散系統的量化反饋控制問題,利用具有可數個固定控制輸入的方法,解決了用“可數”去鎮定“不可數”問題.在文獻[4]中,基于Lyapunov 穩定性理論和線性矩陣不等式研究了包含均勻量化器的非線性系統的一致有界穩定問題.文獻[5-6]針對具有量化輸入的非線性系統,研究了自適應控制問題.

在工程實踐中,系統的暫態性能是非常重要的.一般來說,為了提高生產效率,要求系統滿足一定的快速性.如調節時間不能太短,容易造成系統機械沖擊,影響設備使用壽命;反之,調節時間也不易過長,影響生產效率.固定時間控制是一種改善系統暫態性能的有效控制策,保證系統具有快速收斂性的同時,收斂時間存在確定上界,且與系統初始狀態無關.文獻[7]在最早的研究中首次提出了固定時間穩定的概念.基于此,文獻[8-9]研究了非奇異固定時間控制問題,給出了固定時間收斂控制器的設計方法.文獻[10]針對一類具有模型不確定性和外部擾動的時變非線性系統,研究了固定時間收斂特性的終端滑模控制問題.文獻[11]研究了具有輸出受限多輸入多輸出非線性系統的自適應固定時間控制問題.當前,隨著對模糊控制/神經網絡技術研究的不斷深入,非線性系統自適應模糊控制和神經網絡控制相關成果不斷涌現,尤其利用反演控制算法,設計了很多不同的自適應控制算法解決非線性系統控制問題[12-15].

上述文獻提出的方法有效地解決了某些特定非線性系統控制問題,然而針對非線性系統的模糊自適應控制尚有研究空間.例如,針對非線性系統的模糊自適應固定時間量化反饋控制,成果不多.因此,受上述文獻啟發,本文將固定時間控制、量化反饋控制及模糊控制等相結合,基于李雅普諾夫有限時間穩定理論和反演控制算法,研究具有遲滯量化器的非線性系統實際固定時間量化反饋控制問題.擬解決如下問題:1) 針對一類嚴格反饋不確定非線性系統,提出一種使系統實際固定時間穩定的控制策略,能夠保證系統的跟蹤誤差在固定時間內收斂于原點的一個很小鄰域內,且收斂時間與系統初始狀態無關;2) 針對具有遲滯量化器的非線性系統,利用反演控制算法,基于李雅普諾夫有限時間穩定性理論,設計模糊自適應量化反饋控制器,使得閉環系統的所有信號均有界.最后,通過一個仿真示例驗證了設計方法的有效性.

1 系統描述及預備知識

1.1 系統描述

考慮如下一類嚴格反饋非線性系統

其中,(t)=[x1(t),···,xi(t)]T∈Ri,i=1,···,n,y(t)∈R分別表示系統的狀態變量及輸出變量;gi(·),fi(·)為原點鄰域內未知光滑非線性函數.

為了增加新的量化水平、避免量化信號的快速切換及抖振問題,本文選取如下遲滯量化器[16]

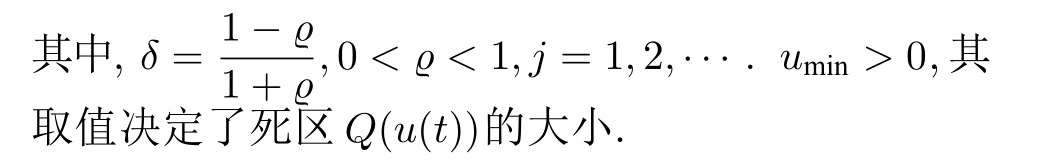
本文的控制目標為:確定區間Ω={0,±uj,±uj(1+δ)}和控制輸入u(t),使得量化反饋控制器Q(u(t))確保系統的跟蹤誤差在固定時間內收斂于原點的一個很小鄰域內,并且閉環系統的所有信號實際固定時間穩定.

根據文獻[17],量化輸入Q(u(t)) 可以描述為

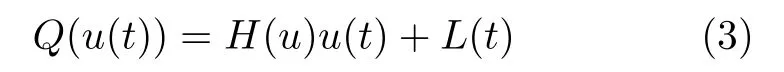
且滿足如下條件

1.2 預備知識

下面的定義、引理及假設對系統自適應實際固定時間量化反饋控制起了重要作用.

定義1[18].考慮系統

其中,x(t)∈Rn是系統的狀態變量,f(·)為光滑非線性函數.若系統(6)是李雅普諾夫意義下穩定,若存在有限收斂時間Ts(x0),對于所有時間t ≥Ts,x(t)=0 恒成立,且收斂時間Ts存在與狀態變量無關的確定上界,則該系統是固定時間穩定的.

引理1[18-20].考慮系統(6),若存在正定函數V(x)及正實數μ1,μ2,χ ＞1,0＜? ＜1,滿足

則稱系統(6) 是固定時間穩定的,其收斂時間為

進一步,若存在正常數1,1 和0＜＜∞,使得

成立,則該系統是實際固定時間穩定.

注1.為了證明推導方便,在后面的設計過程中,令引理1 中的參數?=1,χ=0.75,?=2.

引理2[21].對于x∈R及?ε＞0, 滿足

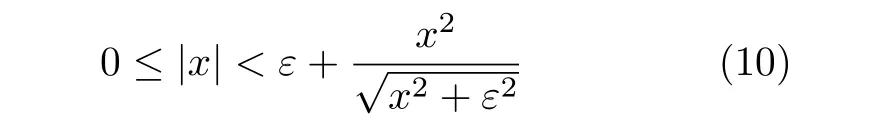
引理3[19].κi∈R,i=1,···,n及o∈(0,1],有

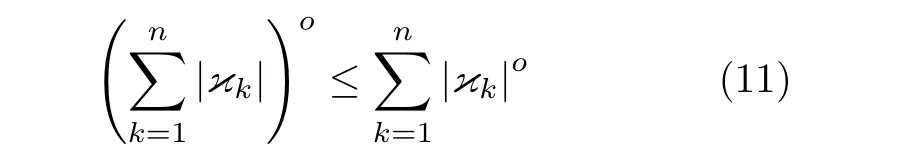
引理4[11].對于xi≥0,下列不等式成立

引理5[22].對于o1＞0,o2＞0,o3＞0,γ1≥0,γ2≥0,γ3≥0,如下不等式成立

引理6[11].對于任意的?＞0,下式成立

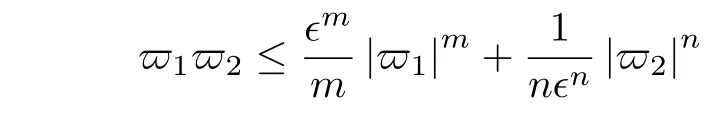
其中,m＞1,n ＞1 且(m-1)(n-1)=1.

引理7[22].函數f(Z):Rq→R是在緊集 ΩZ中定義的連續函數,對于任意常數τ＞0,存在模糊 邏輯系統WTR(Z)使得

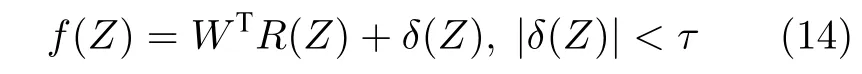
其中,δ(Z)為逼近誤差,W=[w1,w2,···,wl]T∈Rl表示權值向量,R(Z)=[r1(Z),r2(Z),···,rl(Z)]T,ri(Z)=exp[-(Z-?i)T(Z-?i)/]是模糊基函數向量,這里,i=1,2,···,l,?i=[?i,1,?i,2,···,?i,l] 是基函數的中心,ηi是基函數的寬度.

假設1[11].系統(1)中的函數gi(·)(i=1,···,n)有界,即:存在正常數0,使得

不失一般性,假設gi(·)為嚴格正的.

假設2[11].輸出跟蹤信號yr(t)及其直到n階導數 均為連續有界.

2 控制器設計

2.1 設計過程

本節中,應用反演算法,在假設1 和假設2 下設計實際固定時間跟蹤控制器.首先,引入如下坐標變換

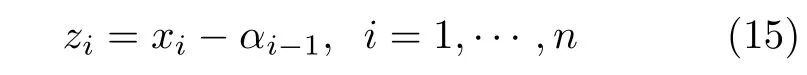
其中,αi-1是虛擬控制律,α0=yr.整個控制器設計過程分n步,具體為:

步驟1.根據式(1)和式(15),有

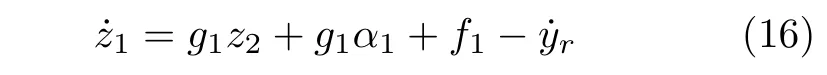
考慮如下Lyapunov 函數

其中,=θ1-,是θ1的估計,r1為大于零的設計參數.

它的時間導數為

其中,δ1(Z1)為逼近誤差,Z1=[x1,yd,].

利用完全平方公式,z1Λ1可以表示為

其中,θ1=‖W1‖2.將式(20)代入到式(18),得到

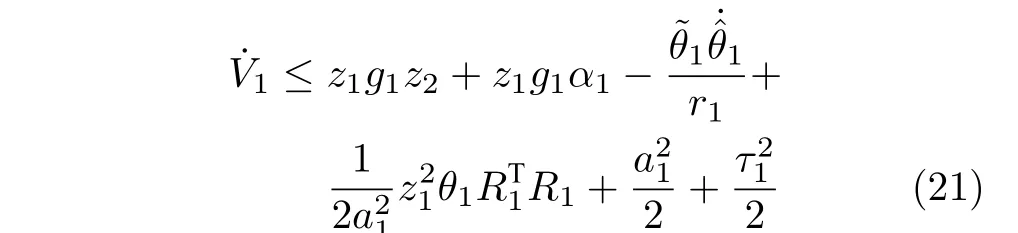
設計第1 個子系統的自適應律和虛擬控制律α1為

其中,a1,K11,K12,κ1,ε1均表示正的設計參數,且Sz1定義為

其中cj(j=1,···,n)各系數由如下方程計算求得:

注2.上述分析過程僅考慮了當|z1|≥ε10的情形.當|z1|＜ε10時,通過重復上述的分析過程,可以得出式(27)中存在一個有界的附加項,其可以看作是式(27)中常數項σ1產生的一個微小增量.為了討論方便,在理論分析過程中僅討論|zi|≥εi0的情況.

步驟i(2≤i ≤n-1).考慮第i個子系統,對zi求導得

定義李雅普諾夫函數Vi為

計算Vi的導數,得

根據完全平方公式,如下不等式成立

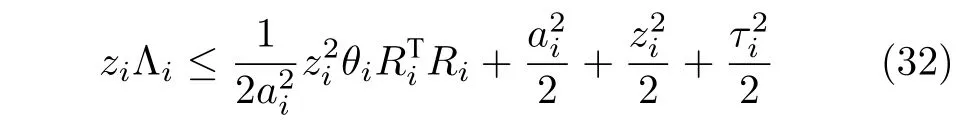
其中,θi=‖Wi‖2.

設計自適應律和虛擬控制αi為

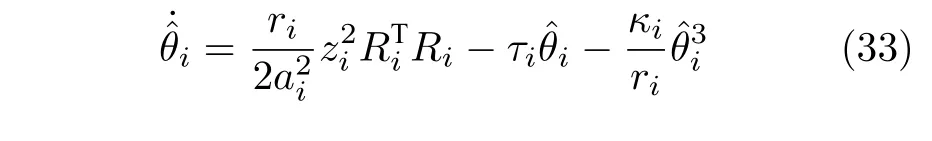
其中,參數cj的取值與式(25)相同.

根據式(34)和式(35),得

結合式(30)～(37),如下不等式成立

步驟n.構造李雅普諾夫函數

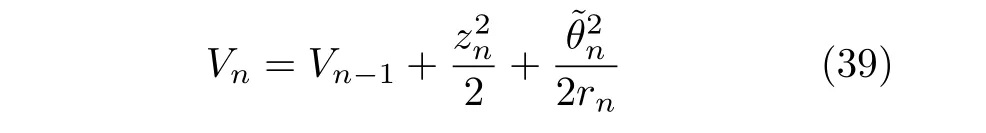
利用式(15),于是

結合式(3)和式(40),計算Vn的導數,得

利用完全公式,式(4)和式(5),如下不等式成立

其中,θn=‖Wn‖2.

將式(42)和式(43)代入式(41),得到

其中,an,Kn1,Kn2,κn,εn均為大于零的設計參數,且Szn定義為

根據式(4),式(46)及引理2,得

將式(45),式(47)和式(49)代入式(44),有

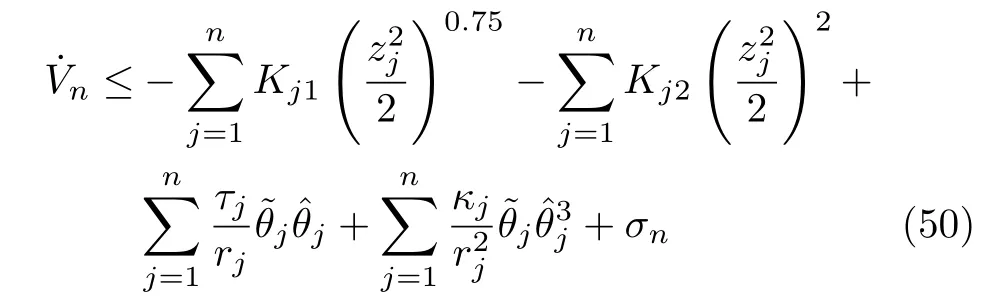
進一步,利用Young 不等式[11],可得

將式(51)～(53)代入式(50),有

顯見,o3是大于零的正常數.

利用引理6,容易得到

將式(57)和式(58)代入式(56),得到

至此,控制器設計過程結束.本文的主要結果可總結為第2.2 節中的定理1.

2.2 穩定性分析

接下來,基于引理1,對系統(1)進行穩定性分析.

定理1.考慮系統(1)在遲滯量化器(2)及滿足假設1 和假設2 的條件下,設計實際控制律(46),并采用式(23)和式(34)所描述的虛擬控制律及式(22),式(33)和式(45)表示的自適應律,則

1) 被控系統(1)內所有信號均有界;

2) 系統的跟蹤誤差在固定時間內收斂于原點的一個很小鄰域.

因此,稱該系統是實際固定時間穩定的.

證明.根據引理1 和式(60),可知Vn有界,進而推出zi,有界.進一步,由式(23),(24),(34),(35),(46)和(47),可知αi及u有界.又因為zi=xi-αi,可確定xi的有界性.綜上,閉環系統內所有信號均有界.

進一步,將式(60)變換成如下形式

3 仿真分析

下面將通過如下算例來驗證本文所設計的控制算法的有效性.考慮如下非線性系統

根據定理1,設計系統(64)自適應固定時間量化反饋控制律.仿真過程中發現,設計參數的選擇合適與否對系統性能有較大影響,通過反復試湊,選擇如下設計參數:K11=K12=10,K21=K22=10,a1=a2=10,ε1=ε2=0.01,r1=r2=0.01,τ1=τ2=0.001,κ1=κ2=1;量化參數選擇如下:δ=0.2,umin=0.1;系統初始條件為x1=0.2,x2=-0.5,=0.4,=0.1.

圖1 表示系統實際輸出和期望輸出響應曲線,圖2 繪制了跟蹤誤差響應曲線,從仿真結果可以看出,,跟蹤誤差收斂于原點的一個小鄰域內.圖3～6 分別為系統狀態x2、控制輸入u、量化輸入Q(u)及自適應在固定時間內律的響應曲線,表明系統內所有信號均是有界的.仿真結果表明該系統是實際固定時間穩定的,驗證了設計方案的有效性.

圖1 期望輸出和實際輸出曲線Fig.1 Trajectories of desired output and practical output

圖2 跟蹤誤差響應曲線Fig.2 Response curve of tracking error

圖3 狀態變量x2響應曲線Fig.3 Response curve of x2

圖4 控制輸入 u 響應曲線Fig.4 Response curve of control input u

圖5 量化輸出響應曲線Fig.5 Response curve of Q(u)

圖6 自適應律,響應曲線Fig.6 Response curves of adaptive control law ,

4 結論

本文針對具有量化輸入的一類嚴格反饋非線性系統,基于有限時間Lyapunov 穩定理論和模糊控制方法等,研究了非線性系統的模糊自適應實際固定時間跟蹤控制問題.所設計的控制器能夠保證系統的跟蹤誤差在固定時間內收斂于原點的一個小鄰域,同時保證閉環系統內所有信號有界.仿真算例驗證了所提控制方案的有效性.值得指出的是,本文所得到的結果是在假設控制系統的所有狀態變量可測的前提條件下成立,然而該假設條件在許多實際系統中難以滿足.為此,下一步將考慮在狀態不可測的條件下,研究基于狀態觀測器的固定時間輸出反饋控制問題.