地震動全非平穩時頻譜統計模型及其在結構分析中的應用

何浩祥，丁佳偉，閆維明

（北京工業大學工程抗震與結構診治北京市重點實驗室，北京100124）

引言

地震動是復雜的非平穩隨機過程，其隨機性主要來自于震源機制、傳播途徑和局部場地條件，且時域和頻域的非平穩性都比較明顯。地震動的基本特性可以通過振幅、頻譜和持時三要素來描述。該三要素從時域頻域兩方面刻畫了地震動特征，是影響結構響應的主要因素。通常采用強度包絡函數來描述地震動時域幅值的變化特征，常用的數學模型主要分為單峰函數型［1-2］和分段函數型［3］兩類。單峰模型不適用于描述多峰型地震動波形，分段連續模型對于描述沖擊型地震記錄不恰當，并且在分界點處不光滑。由于不同地震動持時和峰值出現時刻各不相同，直接對大量地震動進行統計分析難以獲得簡潔直觀的模型，因此上述模型都是根據部分典型地震動波形和觀察經驗確定的，并不直接具有明確的統計特征。如何確定具有統計意義的地震動強度包絡函數模型具有重要的研究意義。此外，地震動在頻域上也具有顯著的非平穩特性，通常采用功率譜來描述其頻譜特性，以表征地震動在不同頻率成分上的能量分布。常用的多種功率譜模型均以Kanai-Tajimi［4］譜為代表的過濾白噪聲型功率譜為基礎進行適當調整以抑制低頻或高頻成分［5-6］。但以上功率譜模型均為光滑的單峰曲線，與真實地震動功率譜差別較大，對非平穩的表征不夠充分和細致。綜上所述，傳統時域或頻域理論模型不能充分地反映地震動時頻域的非平穩性。

時頻分析是一種將時域信號映射到時頻空間描述和表達的方法，在信號局部或瞬態特征刻畫方面具有獨特的優勢。由現代時頻分析方法獲取的時變功率譜能夠從時間、頻率和幅值三個方面來共同描述非平穩隨機過程的時頻局部特性［7-9］。目前計算時變功率譜的方法主要有短時Fourier變換、WVD（Wigner-Ville Distribution）分解、經驗模態分解以及小波變換和小波包變換等［10-11］。雖然時頻分析方法眾多，但大部分方法在處理地震動信號時并不能充分滿足時域和頻域的邊緣條件，仍然不夠精確。文獻［12］通過對比分析確認了具有合適基函數的小波包分解方法可準確描述地震動的時頻變化特征，是建立時變功率譜（演變譜）準確而有效的工具。然而，目前尚缺乏反映各類場地條件影響的具有統計意義的時變功率譜模型或精準的經驗公式，這制約了時變功率譜在地震動特性分析中的深度應用。

此外，目前的結構隨機振動分析理論雖然通常根據演變譜理論進行求解，但一般都進行了簡化處理。采用的地震動模型通常為均勻調制模型和傳統非均勻調制模型，前者沒有考慮頻域非平穩性而后者對非頻域平穩性的反映不精確、不充分，影響了結構地震隨機振動分析的精度。

有鑒于此，本文提出了基于能量持時的地震動強度統計模型建立方法，獲得了不同場地類型下的地震動強度包絡統計模型。在此模型基礎上提出了多峰型功率譜模型和全非平穩時變功率譜模型，并根據非平穩信號的邊緣條件和能量非負性驗證了其精確性，為建立精確的地震動時變功率譜統一模型并進行精確的結構隨機響應分析提供堅實基礎。結構隨機振動分析算例結果表明：采用傳統的隨機振動分析方法的結果偏保守且不夠準確，而基于精確時變功率譜（演變譜）計算得到的結構響應能夠準確而細致地反映時頻兩域非平穩性的影響，適宜在地震動分析和結構動力分析中推廣。

1 基于能量持時的地震動強度統計模型

地震動在時域上呈明顯的強度非平穩性，可采用隨時間變化的加速度強度包絡函數來描述振幅變化過程。目前強度包絡函數模型主要分為單峰型函數模型和多段式強度包絡函數模型［3］。前者的典型公式包括：

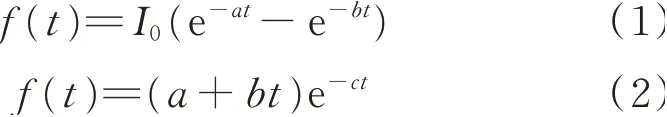
式中t為時間；I0，a，b和c均為特征參數。

在多段式強度包絡函數模型中，三段式模型最為常用，其表達式為

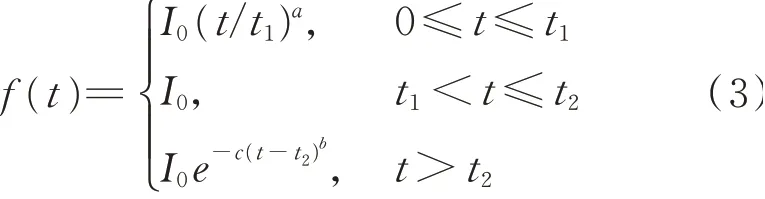
式中a，b，c均為模型參數，t1和t2分別為控制強震平穩持續段的首末時刻。

傳統的強度包絡函數模型都是依據一定的典型地震記錄或經驗建立的，并未從波形統計特征方面進行確切驗證，具有一定的局限性，需要根據大量數據建立具有統計特征的強度包絡曲線。在獲取地震動強度包絡統計值時，由于不同地震記錄下的峰值出現時刻和平穩持時段均不同，如果直接將每條地震波的絕對值的最大值對齊，疊加后的總波形平穩段將交叉混疊，并不具有真實性和代表性，也無法應用傳統的強度包絡函數來表示。

實際上，強度包絡函數的定義中隱含著對累積能量及持時的規定，能量持時定義為地震動加速度能量累積達到兩個不同閾值之間的時間差，其中能量累積過程由地震動加速度平方的積分表示［13-15］。能量持時可按下式計算

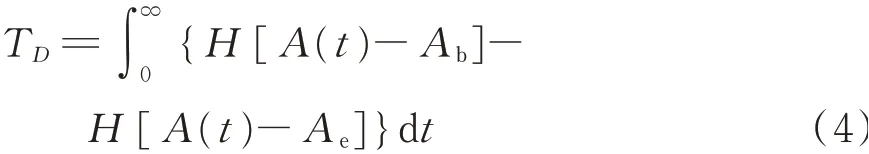
式中H為Heaviside函數，Ab和Ae分別為第一個和第二個閾值，A（t）為歸一化的Arias強度，計算公式如下

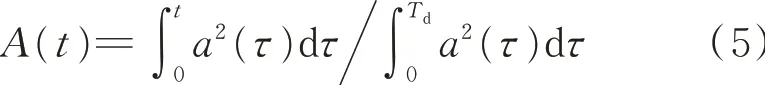
式中a（τ）為地震動加速度記錄，Td為地震動總持續時間。

基于強度包絡函數模型實際上是對累積能量持時的表達這一觀點，本文提出基于能量持時的地震動強度統計模型建立方法，可以將大量地震記錄的強震平穩持時段集中匯集在一起并使強度模型具有統計特征。該方法的具體步驟為：（1）將各類場地大量的地震記錄進行歸一化處理；（2）通過公式（4）和（5）分別計算不同場地類型下每條地震記錄累積能量的起始閾值點tb及終止閾值點te；（3）計算每條地震記錄起始與終止閾值點的中心時刻tm；（4）確定各類場地中所有地震記錄中心時刻tm的最大值tmax，并以此為基準將各條地震記錄的中心時刻tm與tmax對齊，視為同一時段發生的地震記錄；（5）由于各地震記錄的時程長度不同，將地震記錄的起點時刻補零找齊，使地震記錄時程具有相同長度，并構成整體疊合記錄；（6）對上述疊合記錄取絕對值并歸一化，最終得到具有統計意義的等效波，之后可用擬合方法確定偏差最小的強度包絡函數。上述方法的特點在于：可將地震動的主要能量（強震平穩段）集中在有限時域范圍內，為評價能量統計特征提供良好的基本條件；避免了不同地震記錄的持時不同造成的不便；能量對齊之后地震動峰值仍然在適當的時域范圍內，在此基礎上進行峰值分析、平滑處理和建立強度包絡更有統計意義。

為了驗證上述方法的有效性，針對四類場地按照如下的要求從太平洋地震工程研究中心（PEER）數據庫中選波：1）所選地震震級應大于3.5級；2）地震波的PGA大于0.05g小于0.8g；3）震中距大于10 km小于240 km；4）平均土層剪切波速符合規范的要求；5）一次地震發生最多采用2條不同地點的地震記錄；6）均采用水平向的記錄。分別選取了世界范圍內的100條典型的地震記錄進行統計分析并建立強度包絡模型。分析結果證明5%到75%的累積能量持時段包含了地震的強震的主體［13］，是震動最強和破壞力最強的部分，因此通過式（4）和（5）計算每條地震記錄的5%和75%的能量閾值。以Ⅱ類場地和Ⅳ類場地的統計結果為例，如圖1所示。可以看出，按照本文方法獲得的基于能量持時的地震動時程曲線既保留了每條地震記錄的變化趨勢，又保證了總體的模型特征，細致而全面地表征了不同場地條件下的地震波強度演變特征。該方法克服了最大峰值對齊方法帶來的波形多峰和交錯現象。同時，相關結果表明基于能量持時的地震動強度統計波形確實呈現出與傳統強度包絡函數模型一致的變化趨勢。分別采用單峰型函數模型和三段式函數模型對四類場地的統計地震記錄進行擬合，并計算擬合誤差，結果如表1所示。可見誤差均很小，采用兩種模型均具有較高的精度，因而傳統模型確實具有良好的普適性。根據本文方法獲得的強度時程曲線和相關包絡函數模型準確有效，并具有統計意義，可以為今后的地震動時頻域非平穩性分析和結構動力分析提供良好的數據支持。

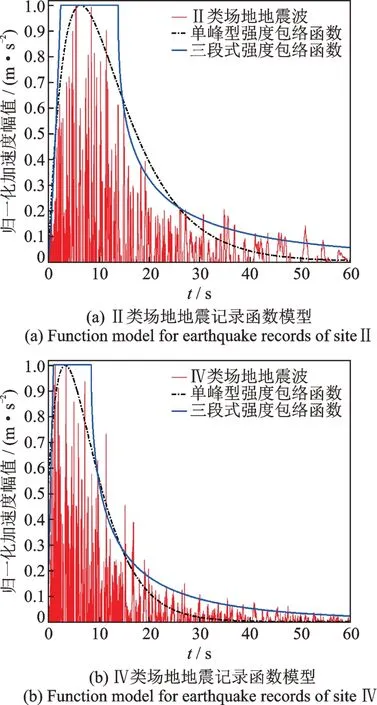
圖1 典型場地地震記錄強度包絡函數模型Fig.1 Envelope function model of seismic record intensity for typical sites

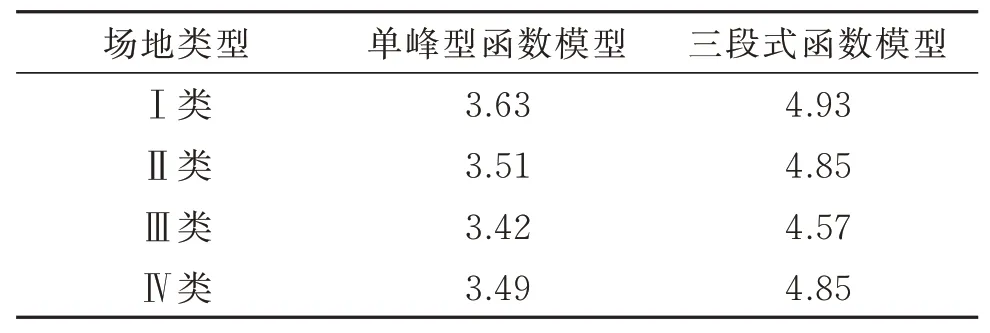
表1 各模型與四類場地地震記錄的相對誤差/%Tab.1 Relative error between each model and four types of site seismic records/%

2 多峰功率譜統計模型

大量地震動特性研究表明：地震動的強度非平穩性及其對結構動力分析的影響固然重要，但地震動的頻域非平穩性更加復雜，對結構隨機動力響應的影響也更深遠。基于上文由統計分析得到的基于能量持時的強度時程曲線，本文將開展多峰功率譜統計模型的研究。

地震動的功率譜在頻域上都是復雜多變的，具有強烈的非平穩性。長期以來，為了分析方便，研究者通常使用以Kanai-Tajimi功率譜及其修正譜為代表的過濾白噪聲模型來描述地震動功率譜，這些譜模型均呈現平滑單峰形狀，不足以精確表征真實功率譜多峰現象和非平穩性，導致地震動的非平穩特性過度簡化且以功率譜模型為基礎的結構隨機振動分析的精度不足。為了解決上述問題，本文采用多峰功率譜函數［16］作為頻域的表達，如下式所示

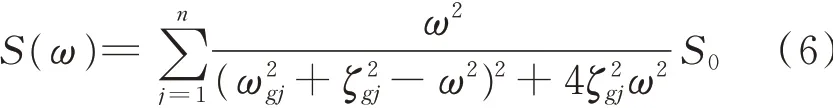
式中S（ω）為多峰功率譜函數，ω為地震動圓頻率分量，n為等效土層數，ωgj和ζgj分別為第j個土層的固有頻率和阻尼比，S0為白噪聲激勵的功率譜密度。上述模型采用Yamada等［17］提出的由多個二階線性濾波器響應之和組成的表達式，反映了地震動通過場地內多個土層的效果，可以精細模擬多峰現象及復雜變化特征，比其他功率譜模型具有更高的精度和準確性，是建立時變功率譜模型的關鍵。對上文基于能量持時的地震動強度統計模型建立方法得到的各類場地100條地震波分別取均值，最終得到各類場地的典型歸一化地震波。根據各類場地代表性歸一化地震記錄的真實功率譜確定多峰平滑功率譜的參數，Ⅰ類至Ⅳ類場地的等效土層數量n依次為18，12，14和16。通過最小平方和誤差的多元函數的目標優化方法可識別功率譜函數模型中的ωgj，ζgj和S0等參數。

為了驗證多峰功率譜函數模型的精度，首先計算得到各類場地的傳統功率譜的譜值，并以此作為真實值，分別采用Kanai-Tajimi譜、Clough-Penzien譜和歐進萍譜對各類場地的結果進行基于滿足最小平方和差的參數擬合，得到相應的等效功率譜，并與多峰功率譜進行對比，其中Ⅱ類場地的對比結果如圖2所示。各功率譜與真實功率譜的相對誤差和確定系數（R-square）如表2所示。

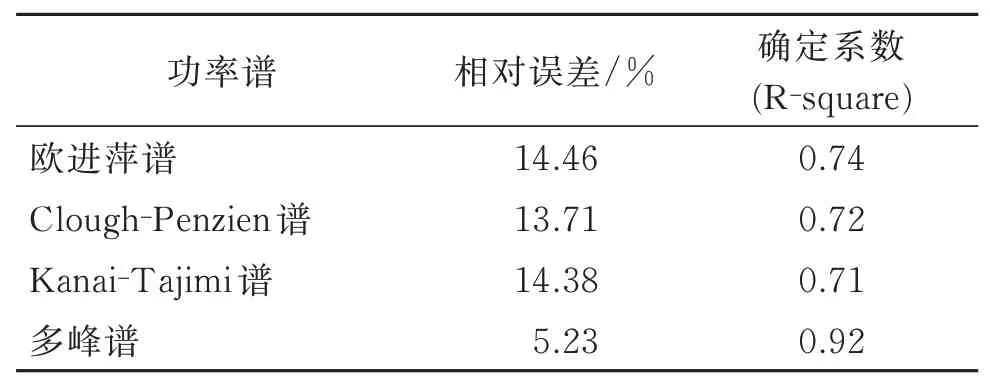
表2 各功率譜與真實功率譜的相對誤差及確定系數Tab.2 Relative errors and R-square of power spectrum and real power spectrum

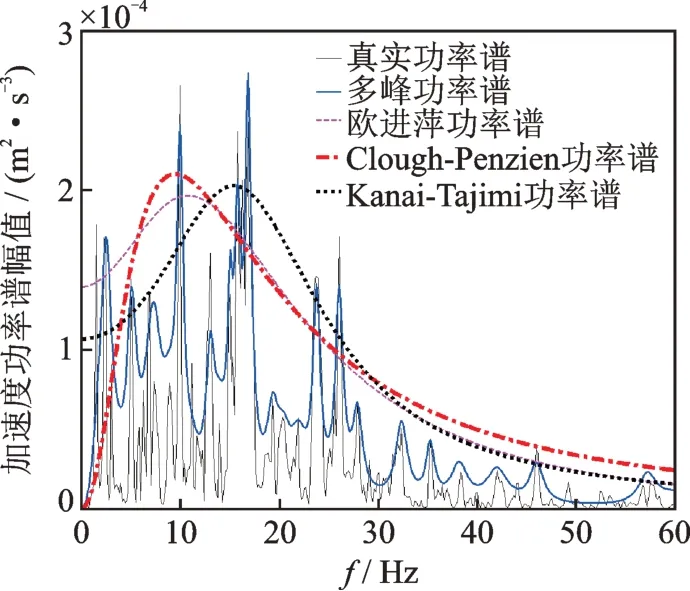
圖2 不同功率譜精度比較Fig.2 Accuracy comparison of different power spectra

從以上結果可以看出：傳統的單峰功率譜與真實值之間存在較明顯差異，僅能粗略地表征頻域能量分布的基本趨勢，并不能精確展現頻域能量的非平穩性及多峰特征。此外，Kanai-Tajimi譜和歐進萍譜沒有抑制低頻能量的分布，這與實際不符，雖然Clough-Penzien譜在低頻處的表征較為合理，但總體上仍偏大于真實功率譜。多峰功率譜與真實功率譜十分接近，全面細致地反映了地震動非平穩特征，且自動避免了單峰譜在低頻和高頻精度上的缺陷。因此，本文提出的多峰功率譜統計模型具有較高的精度，更適合在復雜地震動分析中使用。

3 時變功率譜（演變譜）的要求及特性

地震動在時域和頻域均具有強非平穩性，因此研究地震動的時頻全非平穩性更加全面，也更能反映地震動同時在時頻兩域的演變過程及其對結構響應的影響。利用上文由統計分析得到的基于能量持時的強度時程曲線，下文將開展時變功率譜（演變譜）的統計模型研究。

針對類似地震動這樣的強非平穩隨機過程Y（t），Priestley［18］在Wiener拓廣的廣義Fourier積分的基礎上提出了演變譜模型，其意義在于描述演變隨機過程在某一時刻鄰近的“瞬間”平均能量在頻域上的分布，從而可以用通常的“頻率”與“能量”概念來描繪非平穩隨機過程的譜特性。演變譜可以表示為

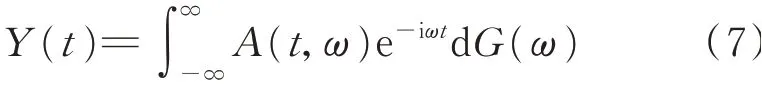
式中G（ω）為一個正交增量過程，A（t，ω）為t與ω的確定性的調制函數。根據正交增量的性質，Y（t）的協方差函數可以表示為

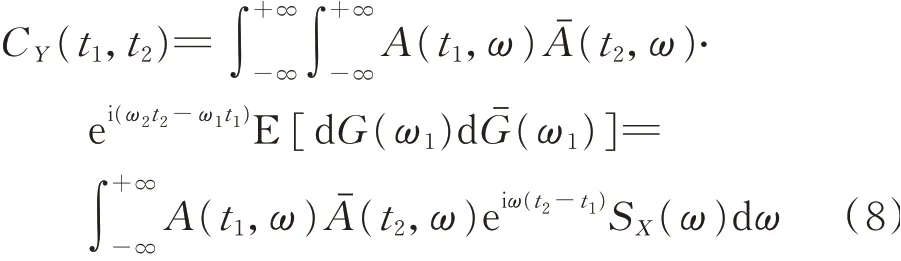
當t1=t2時，可得Y（t）的方差為

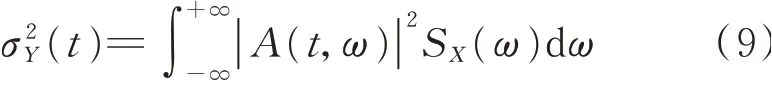
故定義非平穩隨機過程Y（t）的演變譜密度SY（t，ω）如下

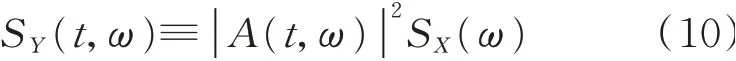
式中SX（ω）為零均值的平穩白噪聲隨機過程X（t）的功率譜，可表示為

式中S0為常數。若設S0=1，則非平穩隨機過程Y（t）的演變譜密度SY（t，ω）可以簡化為

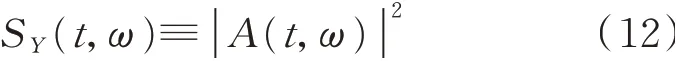
由上述分析可知：對大量地震動進行分析，準確獲取每一記錄的時變功率譜（演變譜），并由此尋求和建立與實際地震動時頻分布統計特征一致的非平穩地震動模型具有十分重要的理論和工程意義。為了確保相關演變譜密度函數的準確性，除了要滿足上述條件外，還應通過信號能量守恒要求及邊緣條件來校核。Cohen［5］根據Parseval定理定義了非平穩信號Y（t）時域和頻域的邊緣條件，表達式如下

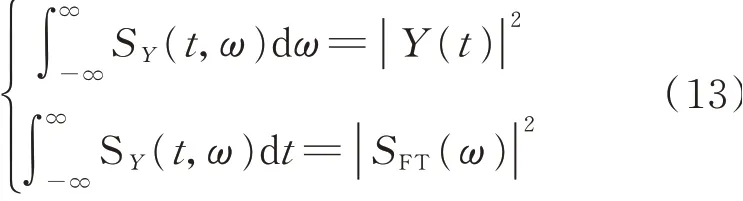
式中SY（t，ω）為非平穩信號Y（t）的時變功率譜，也即演變譜。SFT（ω）為信號的Fourier變換幅值譜。從上式可以看出：信號某一特定時間的所有頻率能量分布之和等于其瞬時能量；信號的某一特定頻率的能量分布在全部時間上的總和等于能量密度頻譜。精確的時變功率譜（演變譜）要滿足上述的邊緣條件。隨著時頻分析研究的進展，研究者提出了關于時頻分布的其他的要求，如時頻分布必須是實的，時頻分布關于時間t和f的積分應該與非平穩信號的總能量E相等，即如下式

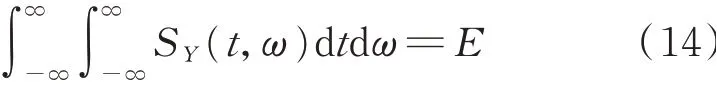
從上述的時頻分布的要求可以看出，邊緣分布的特性和非負性一起保證時頻分布準確反映信號的譜能量、瞬時功率和總能量。邊緣條件要求可以保證信號的總能量（如平均時間、平均頻率、時寬和帶寬）正確給定。非負性則可以進一步保證分布的期望是切合實際的物理解釋。非負性和正確的邊緣分布特性在一起可以保證時頻分布的強有限支撐性。

國內外研究者相繼建立了不同的地震動時變功率譜（演變譜）特性描述方法和模型。Okaya等［19］將平穩和瞬態波譜估計的多重濾波技術拓展到演變譜估計，但由于模型識別參數過程復雜，且精細程度與阻尼比經驗取值有關，限制了其廣泛應用。Nakayam等［20］利用窄帶和低通濾波，直接生成復調制函數從而建立演變譜，但精度有限。Conte等［16］提出了全非平穩時變功率譜函數模型，其假設地震加速度為一個由多個均勻調制過程疊加而成的Sigma振子過程，時變功率譜為各過程的功率譜密度函數的疊加，具有多峰性。該方法在假定地震記錄為平穩高斯過程的疊加存在較大的問題，且模型并不完全滿足時頻域邊緣條件。林家浩等［21］、梁建文等［22］、胡燦陽等［23］和劉章軍等［24］曾分別提出由強度包絡函數和功率譜函數相乘而形成的時變功率譜模型，但其調節能力和多峰性有限，并不能充分反映時頻域復雜的時變特征，同時也不滿足邊緣條件，在研究和工程應用方面存在不足。在進行結構隨機振動分析時，以上模型所得的結構響應與真實結構的結果也存在較大差異。何浩祥等［12］提出采用時域和頻域歸一化邊緣值的誤差標準差來量化和評判時變功率譜的精度，并對短時傅里葉變換、WVD變換、小波變換和小波包變換等時頻分析方法的精度進行了對比，結果表明離散Meyer小波函數的小波包變換具有較好的精度，且滿足邊緣條件及非負性要求，可用來獲得地震動時變功率譜。然而，上述研究是針對具體地震動進行的，并沒有根據大量地震動的分析結果建立具有統計意義的時變功率譜模型。為了進一步研究地震動的時變功率譜的基本規律和通用模型，本文對基于能量持時的地震動強度統計模型建立方法得到的各類場地典型波進行小波包分解，從而獲得相應的時變功率譜，小波包基函數為9層離散Meyer小波函數，結果如圖3所示。通過驗算證明上述的時頻譜嚴格滿足邊緣條件。與地震動時域能量時程或傳統功率譜相比，真實時變功率譜的相對誤差如表3所示。由表可見其誤差非常小，可認為相關時變功率譜能夠從時間、頻率和幅值3個方面準確而全面地描述非平穩隨機過程的時頻特性。

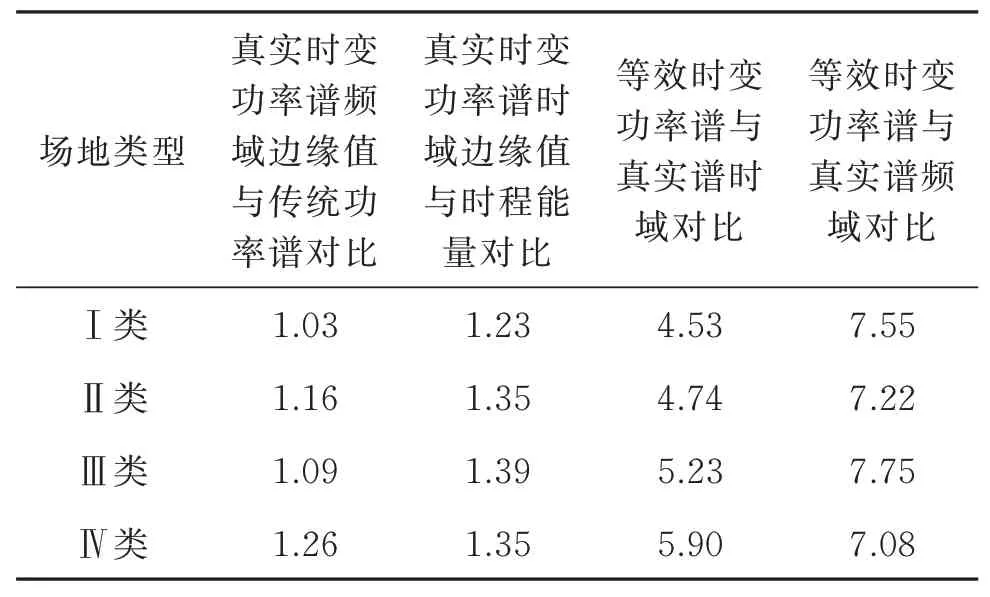
表3 時變功率譜模型相對誤差/%Tab.3 Relative error of time-varying power spectrum model/%

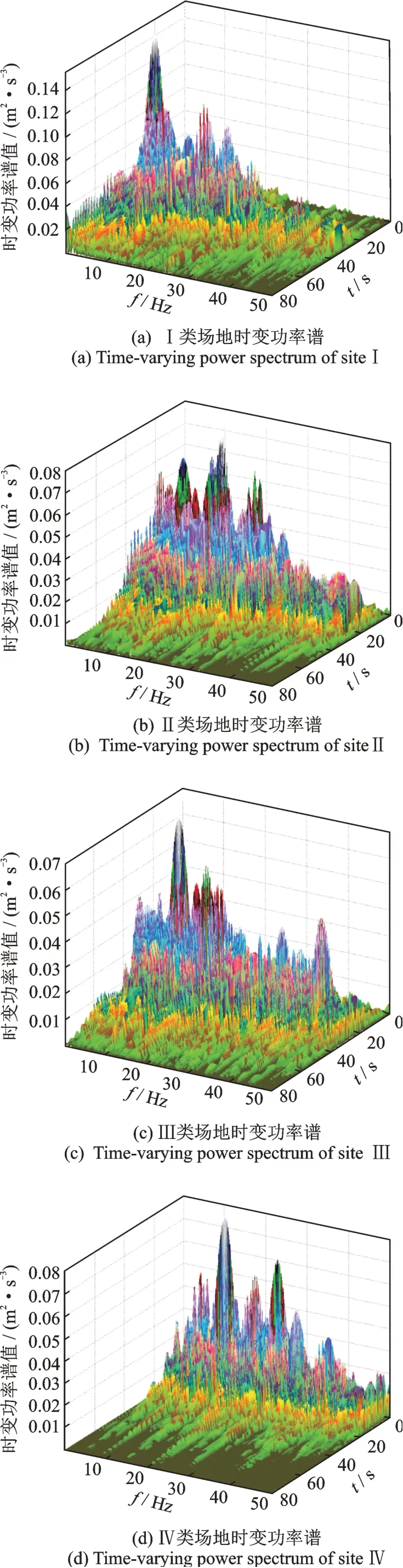
圖3 不同場地下的地震動真實時變功率譜（演變譜）Fig.3 Actual time-varying power spectra（evolution spectra）of ground motions in different fields

經過對地震動真實時變功率譜的深度擬合分析，選用類似式（1）的適用性強的時域強度包絡函數和式（6）的多峰功率譜，本文提出如下時變功率譜等效函數模型

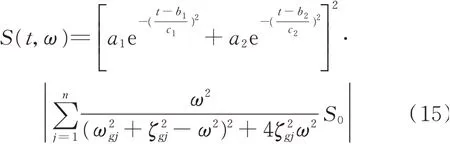
式中a1，a2，b1，b2，c1和c2均為模型的擬合參數。四類場地具有不同的土層模擬值，四類不同場地的時變功率譜結果如圖4所示。

從圖3的結果可以看出：地震動時頻功率譜是十分復雜多變的，時頻分布具有強烈的突變性和隨機性。隨著場地類型的提高，地震動高頻分量所占比例逐漸增長。結合圖4的結果來看，本文提出的時變功率譜等效模型保留了真實時變功率譜的主體特征，剔除了部分噪聲并可較精確地表現多峰現象和時頻域的非平穩基本特性。

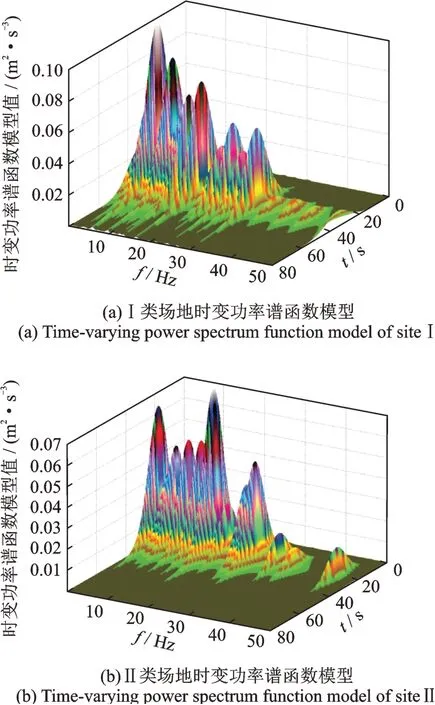
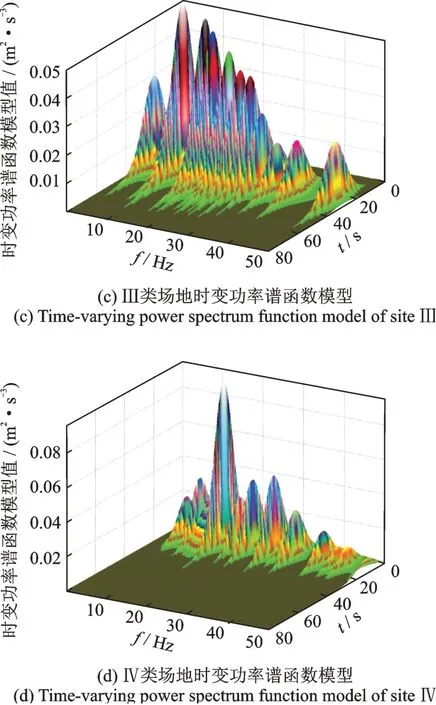
圖4 不同場地下的地震動時變功率譜等效模型Fig.4 Equivalent model of time-varying power spectrum of ground motion in different fields

僅僅依靠時變功率譜本身并不能校核其精確性，為了驗證該時變功率譜等效模型的精度，需要檢驗其是否滿足邊緣條件及非負性。利用式（13），將真實時變功率譜的時域或頻域投影與時變功率譜等效模型的時域或頻域投影作對比并進行誤差分析，Ⅰ類至Ⅳ類場地的對比結果如圖5所示。此外，與地震動時域能量時程或傳統功率譜相比，等效時變功率譜的相對誤差如表3所示。通過對比分析，可以認為等效模型誤差在允許的范圍內，因此本文提出的時變功率譜等效模型可以較精確地表征地震記錄在時頻兩域的非平穩性，且符合時頻分解的邊緣條件特征及非負性，故等效模型具有工程應用價值。

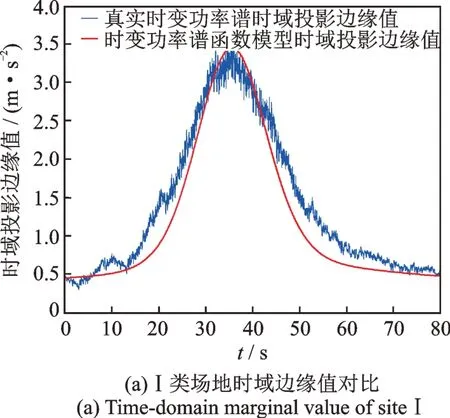
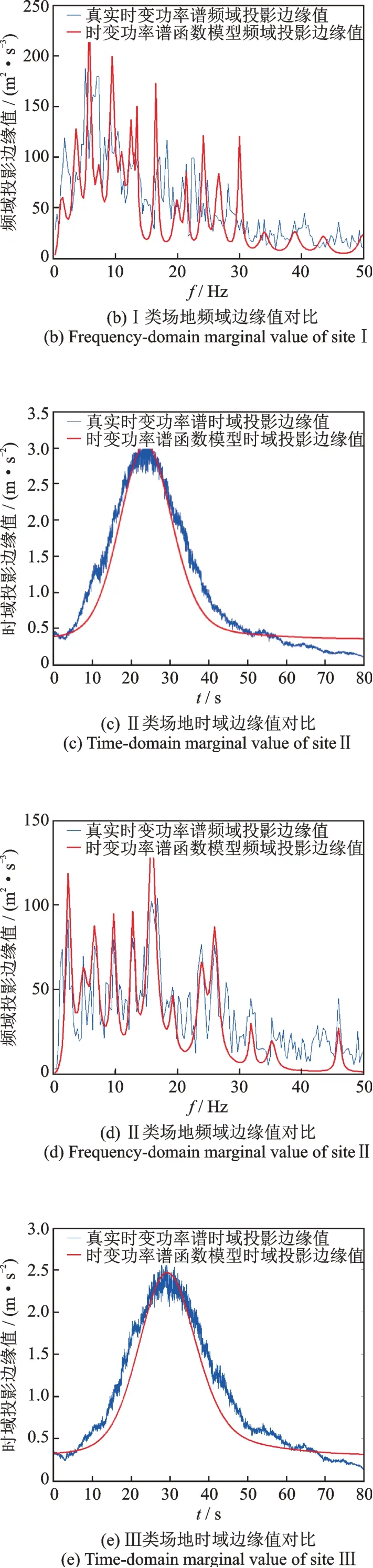
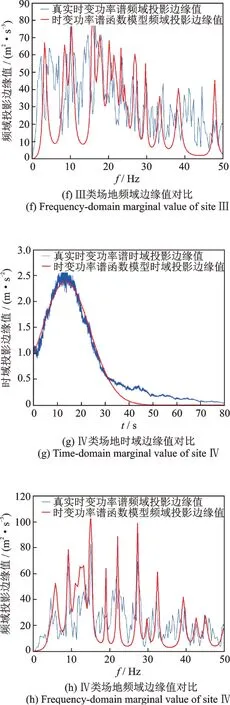
圖5 不同場地的時變功率譜時頻域邊緣值對比Fig.5 Comparison of time-varying power spectrum marginal values in time-frequency domain at different sites

應用本文提出時變功率譜函數模型，根據式（12）可以推得時變調制函數A（ω，t）的函數表達式如下

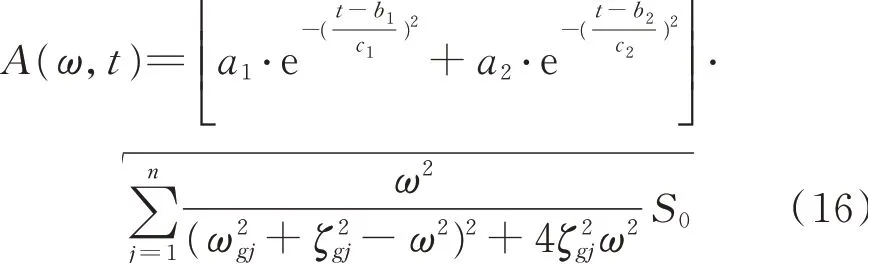
其中演變功率譜的強度調制函數參數如表4所示。

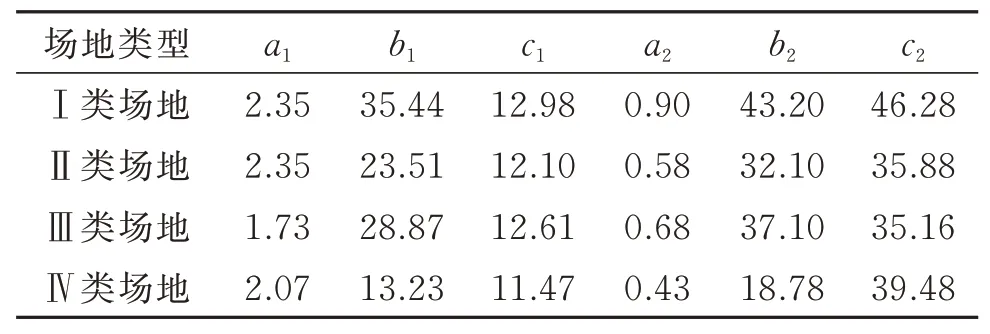
表4 時變功率譜模型強度調制函數參數取值Tab.4 Parameter values of intensity modulation function of time-varying power spectrum model

綜上所述，本文提出的時變調制函數具有良好的精度和適應性，可以實現對時變功率譜的曲面的精細調節和多峰模擬，從而更加細致地刻畫真實的時變功率譜，適合在研究和工程應用中推廣。

4 基于演變譜的結構全非平穩動力分析

應用地震動時頻功率譜（演變譜）模型可以在隨機微分方程均方解的意義下求解結構響應時變過程及其概率特征［25-26］。設結構受時頻域全非平穩隨機激勵引起的響應y（t）表示為

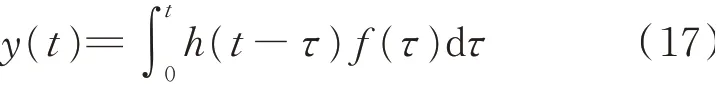
則任意兩個響應量的互相關函數為

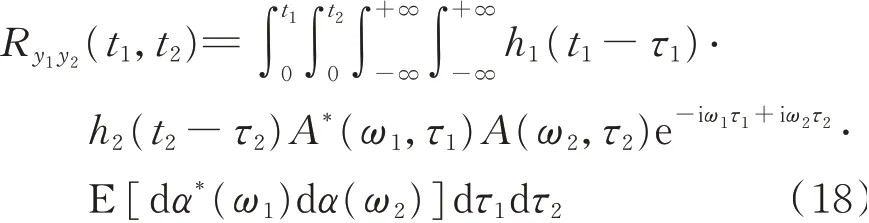
利用正交增量的性質和函數積分的性質得到：

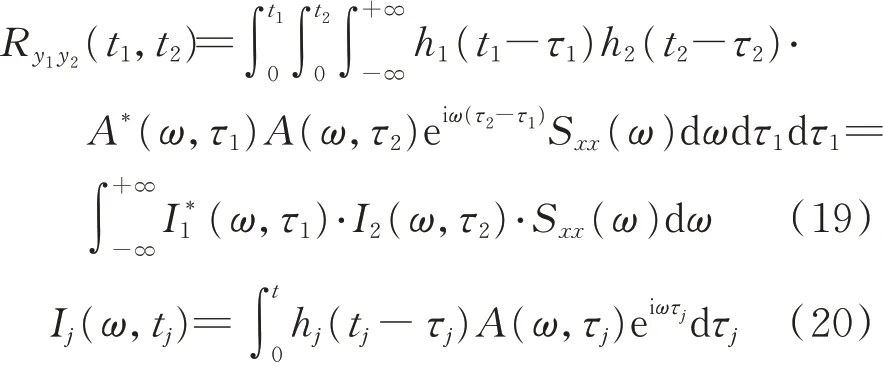
若使t1=t2=t，式（19）右端的被積函數就是y1（t）與y2（t）的互功率譜函數，即

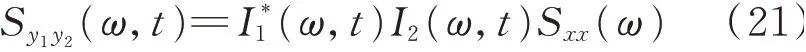
使t1=t2=t，雙非平穩隨機激勵引起的響應y（t）的方差為

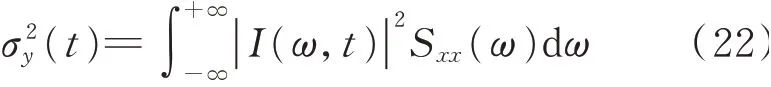
假設外部激勵的自譜密度為Sxx（ω），由此可以構造一個虛擬的確定性的外部激勵

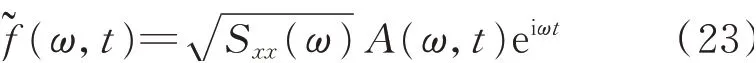
此激勵在t時刻產生的響應為

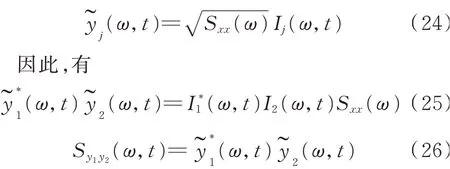
若令y1=y2=y，可以得到任意響應的自功率譜函數計算式如下

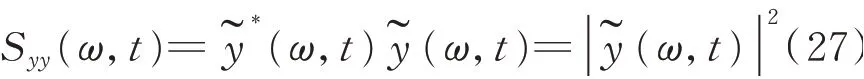
5 算例分析

為了進一步驗證本文提出的時變功率譜函數模型在結構隨機振動分析中的有效性，對一個七層的二維剪切模型框架結構進行隨機振動分析。每層結構層高為3 m，每層均重5.42×108kg，結構阻尼比為5%，基本周期為0.42 s。為了便于比較各種非平穩模型和計算方法的區別，將Ⅱ類場地的典型地震波作為水平向地震動輸入，按照前述方法計算結構地震響應。本文計算所用到的功率譜函數模型如圖2所示，比較當采用真實功率譜（按傳統方法計算得到的功率譜）、時變功率譜、等效時變功率譜、歐進萍功率譜、Clough-Penzien功率譜及Kanai-Tajimi譜的情況下，分別在非平穩強度包絡曲線（原始地震動時域包絡）與光滑強度包絡曲線（對原始時域包絡進行單峰函數擬合）下進行結構隨機響應分析。考慮全非平穩時頻譜情況下，功率譜為時變功率譜或等效時變功率譜，其結構位移標準差按式（22）計算，其中一層和七層的位移標準差曲線如圖6和7所示。當功率譜為真實功率譜、歐進萍功率譜、Clough-Penzien功率譜及Kanai-Tajimi譜時，可采用一般的演變譜簡化計算方法，即式（20）中的A（ω，t）被簡化為時域強度包絡曲線g（t），相應結果如圖6和7所示。

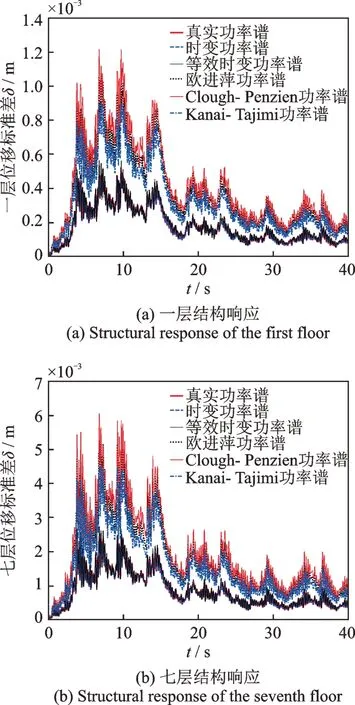
圖6 非平穩強度曲線包絡底層與頂層部位移標準差比較Fig.6 Comparison of standard deviations between enveloped bottom and top layers of non-stationary strength curve

從以上結果可以明顯的看出：根據時變功率譜和等效時變功率譜計算的結構響應與根據真實功率譜計算的結構非常接近，均可視為精準結果，可根據研究需求合理選用。基于傳統過濾白噪聲單峰模型功率譜的結構響應顯著大于全非平穩條件下的結果，其原因在于單峰型光滑功率譜的譜值均大于真實功率譜，沒有真實細致刻畫功率譜的變化特征。此外，結構的響應與功率譜和強度包絡形狀密切相關，功率譜的幅值和形狀直接影響結構位移響應的幅值，而強度包絡函數形式直接影響結構位移響應曲線的變化趨勢。因此，在結構隨機振動分析時，若對結構響應的幅值（極值）精準度要求較高，需要選擇更精確的多峰功率譜模型；若對響應時程的變化趨勢精準度要求較高，需要著重選擇變化細致的強度包絡模型。

為了進一步的對比不同方法的差異，建立層數分別從1到25的25個二維剪切型鋼筋混凝土框架結構并進行隨機振動分析，假定各結構的無阻尼基本周期為0.06n（n為相應總層數），阻尼比均為5%。提取基于各方法的所有結構頂層位移標準差最大值，與真實功率譜的計算結果相對比如圖8所示。

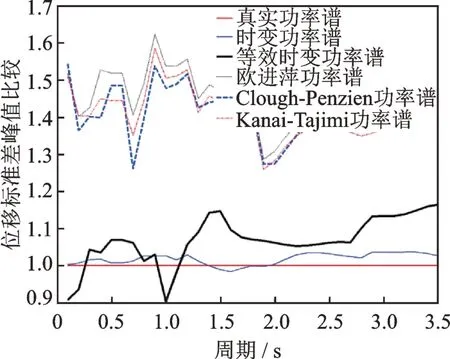
圖8 具有不同周期的結構響應精度比較Fig.8 Comparisons of structural response accuracy with different periods

可以看出：對于不同的周期結構，時變功率譜與傳統功率譜的計算結果均十分相近，可視為精確結果。等效時變功率譜的結果一般有±10%之內的偏差，是可以接受的。而基于傳統單峰功率譜的結果均遠大于真實功率譜的結果，最大偏差在60%以上。在結構設計和分析中，可認為根據以上單峰譜計算的結構響應是不精確或偏于保守的，不宜在此基礎上再考慮安全系數。

綜上所述，本文提出的時變功率譜函數模型及其等效模型，不僅滿足時頻譜的邊緣條件要求，并且更加真實、準確、細致地對地震動全非平穩性進行了描述。經過在結構隨機振動分析中與基于傳統單峰功率譜的演變譜計算方法相比較，進一步驗證了本文的時變功率譜函數模型的精確，且可以在工程實踐中推廣。

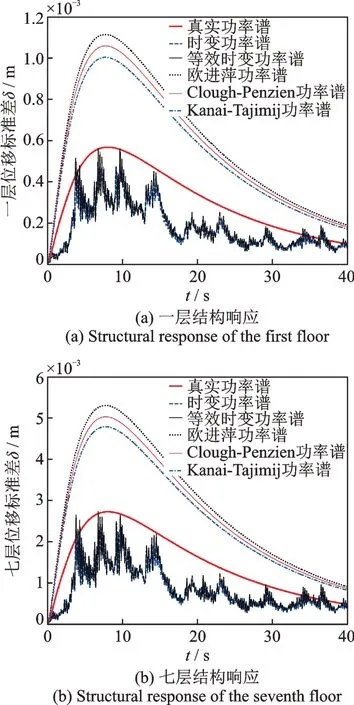
圖7 光滑強度曲線包絡下底層與頂層部位移標準差比較Fig.7 Comparison of standard deviation of bottom and top displacement with smooth strength curve

6 結論

傳統的地震動時域強度包絡函數均為經驗函數，缺乏足夠的統計意義。本文提出了基于能量持時的地震動強度統計模型建立方法，該方法保留了各條地震記錄的變化趨勢、主體特征和樣本特性。經過驗證，該方法適用于各類場地的大量地震記錄的分析，為研究地震動強度的統計特性提供了基礎。針對傳統單峰模型功率譜偏于簡化和保守導致精度不足的局限，多峰功率譜可以細致表征有效頻率范圍內功率譜幅值的變化趨勢，適用于對地震分析精度要求較高的地震動研究及大型復雜結構設計。鑒于傳統時頻分析得到的時變功率譜缺乏精確的統計模型和解析表達式，本文基于多峰功率譜模型建立了時變功率譜統計模型及其等效模型，在時域和頻域方面均滿足能量的非負性及邊緣條件的性質，且精度較高。經過進一步的地震動特性分析和結構隨機動力分析驗證，認為基于歐進萍譜、Clough-Penzien譜及Kanai-Tajimi譜的地震動特性和結構響應與采用真實功率譜的結果差距明顯，而時變功率譜統計模型及其等效模型均具有足夠的精度，可為今后的地震動特性研究和結構動力分析提供更好的技術支持。