地下空間結構對鄰近地上結構地震反應影響振動臺實驗

程 業，潘旦光,2，陳清軍，付相球，李雪菊

(1. 北京科技大學土木系，北京 100083；2. 城市地下空間工程北京市重點實驗室，北京 100083；3. 同濟大學土木工程防災國家重點實驗室，上海 200092)

在地震作用下，大型地下空間結構的存在顯著地影響鄰近場地的地面運動從而影響鄰近建筑的地震反應[1?2]。為分析地下空間結構的局部場地效應，及由此導致地上結構地震反應的變化規律，國內外學者分別采用解析解、數值解和振動臺實驗進行廣泛的研究。

Lee 等[3]和梁建文等[4? 6]采用解析法得到彈性半空間中單個洞室、多個洞室的地震反應問題，計算結果表明地下洞室易使鄰近場地地面位移幅值增大。地下空間結構、地基土以及鄰近地上結構構成了一個復雜的相互作用整體，影響該體系地震響應的因素較為復雜。Guo 等[7]采用廣義層間位移譜分析方法研究了地鐵車站對地上結構響應的影響，結果表明建筑物自身動力特性和建筑物與車站的間距是關鍵影響因素。Wang 等[8]采用數值計算方法研究了地下結構-土-地上結構相互作用中地上結構形式、地震波的入射方向、地下結構和地上結構的距離、土體剪切波速、地下結構的埋深等對結構地震反應的影響，而其中地上結構形式和地震波的入射方向是兩個最重要的因素。Abate 等[9]對隧道-土-地上結構體系進行了數值分析研究，結果表明淺埋隧道場地表面相比自由場加速度降低，深埋隧道下加速度放大；地上結構位于隧道正上方時地震反應最大，場地對于地上結構輸入頻率的濾波作用在隧道-土-結構體系中非常重要。Li 和Chen[10? 11]對互相臨近的地鐵隧道和高層結構模型進行了三維耦合動力分析，研究表明地上結構的存在會降低車站的響應，地鐵站和隧道的存在增加了附近地面的峰值加速度。

由于土-結構相互作用體系的影響因素很多且非常復雜，為驗證理論模型的有效性，常采用實驗進行驗證[12?14]。國內外學者在土-地上結構相互作用和土-地下結構相互作用已開展較多振動臺模型實驗[15?19]。土-地下結構相互作用振動臺實驗通常側重于地下結構的動力反應和破壞情況，同時也觀察到地下結構對地面運動的影響。Abuhajar等[20? 21]結合離心機振動臺實驗和數值模擬進行了土-涵洞動力相互作用研究，結果表明土-涵洞相互作用降低了地面的運動輸入。陳國興等[22? 23]研究表明地下結構的對周邊土體的地震動頻譜特性有顯著的影響，在近、遠場地震動作用下模型地基土加速度反應的頻譜特性和放大效應有顯著差異。Chen 等[24]研究發現脈沖形式的輸入波增大了地鐵站和周圍場地的動力響應，這主要是由于其固有的豐富的低頻成分和高能量。Wang 等[25]對隧道-土-地上結構的振動臺實驗研究表明隧道的存在一定程度上阻礙了地震波的傳播，從而降低了中低樓層地上結構的地震響應。

為研究地下空間結構導致地震動變化對地上結構地震反應的影響，潘旦光等[26]首先開展了地下結構-土相互作用的振動臺實驗，實驗結果表明在水平地震輸入下地下空間結構場地兩側各一倍寬度范圍內有明顯的豎向振動，且地表水平地震動可達自由場地震動的1.933 倍。鄰近地下空間結構的地上結構基礎地震輸入與直接位于場地上基礎地震輸入不同，從而導致地上結構地震反應發生改變。為進一步研究地下結構對鄰近地上結構的影響，開展了地下結構-土-地上結構相互作用(SSSI)和土-地上結構相互作用(SSI)振動臺對比實驗。按照幾何相似比為1∶30 進行了地上框架結構和地下空間結構的實驗模型設計和制作，在同濟大學土木工程防災國家重點實驗室的多動能振動臺上進行了6 條不同震中距的基巖波在6 個不同加速度幅值下SSSI 和SSI 的振動臺模型實驗。對比分析了SSSI 體系和SSI 體系下場地及結構動力特性的變化以及地上結構加速度放大系數隨輸入地震波的頻率、幅值等因素的變化規律。在此基礎上，分析地下空間結構對地上結構箱基的平動加速度、搖擺加速度和結構變形分量的影響。

1 實驗概況

如圖1 所示，振動臺模型實驗共分為兩組：1) 地下結構-土-地上結構振動臺模型實驗(簡稱SSSI 實驗)；2) 土-地上結構振動臺模型實驗(簡稱SSI 實驗)。地下結構原型為一個高15 m、寬27 m的地下三層混凝土結構，斷面尺寸為27 m(寬)×15.2 m(高)，柱間距為9 m，結構頂部埋深3 m。地上結構原型為一個6 層框架結構，基礎為箱型基礎，地上部分尺寸為7.2 m×7.2 m×18 m，層高3 m，箱基尺寸為12 m×12 m，深3.6 m。模型箱采用同濟大學孫利民等[27? 28]設計的一個長6.5 m、寬1.5 m、高1 m 層狀剪切箱。剪切箱共分為9 個滑動層，滑動層之間放置有滑動軸承，箱體兩側通過螺栓固定著一個厚度為2 mm 的鋼板，使模型箱產生剪切運動，同時避免箱體扭曲。內壁有一層厚2 mm的橡膠墊，以減少箱體的邊界效應。剪切箱固定于振動臺臺面上，用于研究剛性基巖上單一土層場地土-結構相互作用問題。

圖1 振動臺實驗Fig. 1 Shaking table test

1.1 相似設計

本實驗為文獻[26]振動臺實驗的延續，因此，相似比設計相同，其中設計的幾何相似比為1∶30，結構材料彈性模量相似比為1∶12，加速度相似比為1∶1，由此可導出時間相似比為0.183，其它相似比詳見文獻[26]。實驗中結構通過添加配重塊的方式滿足模型相似律。但涉及到土介質的振動臺模型實驗時，常規條件下的模型相似律因重力場的影響而很難滿足，此外，還要考慮材料本構的相似性，這是非常困難的。因此，本實驗不追求模型體系和原型體系參數嚴格的相似，而是為了較好地反映出地下空間結構對于地上結構地震反應的影響，模型土采用頻率相似的原則進行設計[29]，使模型中地上結構與土層的基頻相接近，來探討地下結構對鄰近地上結構地震反應影響的規律。

1.2 結構模型和模型土

地下結構模型采用文獻[26]中長1500 mm、寬920 mm、高505 mm 的有機玻璃模型，如圖2所示。實測一階頻率為14.14 Hz，二階頻率為57.27 Hz。模型土采用砂和鋸末的質量比為3∶1，密度為985 kg/m3的混合土[30]。土層厚990 mm，分20 層裝填。

圖2 地下結構模型 /mmFig. 2 Underground structure model

框架結構模型平面布置如圖3 所示，模型層高100 mm，柱的尺寸為15 mm×20 mm，樓板厚10 mm，框架結構1 層～5 層每層配重質量為3.30 kg，頂層配重質量為2.67 kg。箱型基礎尺寸為400 mm×400 mm×120 mm。箱基內部配重質量為31.75 kg，箱基頂板上配重質量為23.52 kg。配重完成后，將箱基底板固定約束下，實測前兩階頻率分別為9.97 Hz 和30.18 Hz。

圖3 框架結構模型 /mmFig. 3 Frame structure model

1.3 傳感器布置及實驗加載方案

SSSI 實驗和SSI 實驗的加速度傳感器布置如圖4 所示。SSSI 實驗中地下空間結構位于土箱中部，地下結構兩側距土箱邊緣距離為2.8 m，地上結構位于地下結構邊緣一側0.35 m 位置處。地上結構距離土箱邊緣距離為2.05 m，類似于遠置人工邊界方法進一步減少了土箱邊界效應的影響。SSI 實驗中地上結構在土箱中的相對位置與SSSI實驗中相同。SSSI 實驗共布置了61 個加速度傳感器，傳感器存活率為96.7%，SSI 實驗中共布置了56 個加速度傳感器，傳感器存活率為98.2%。

圖4 加速度傳感器布置圖 /mmFig. 4 Accelerometer layout

實驗中選取近震、中震和遠震6 條基巖波，它們分別為：1971 年2 月9 日San Fernando 地震距離震中21.5 km Pasadena-Old Seismo Lab 臺站的Near-sfern波和130 km Isabella Dam 臺站的Far-sfern 波、1989 年10 月18 日Loma Prieta 距離震中43.94 km Belmont-Envirotech 臺站的Near-lomap 波和83.37 km Point Bonita 臺站的Mid-lomap 波、1999 年9 月20 日臺灣集集地震距離震中168.72 km KAU082臺站的Far-chichi 波和65.79 km TTN025 臺站的Mid-chichi 波。加速度A 幅值為1 m/s2時的時程如圖5 所示。Near-sfern、Near-lomap、Far-chichi、Far-sfern、Mid-lomap、Mid-chichi 的卓越頻率分別為20.5 Hz、8.1 Hz、2.8 Hz、10 Hz、4.2 Hz 和11.6 Hz。

圖5 輸入地震波加速度時程Fig. 5 Acceleration histories of input seismic waves

兩組實驗的加載順序相同，工況1 和工況2分別為峰值加速度為0.1g的白噪聲輸入和5 Hz的正弦波，然后進行0.035g、0.1g、0.2g、0.4g、0.6g、0.9g這6 個荷載幅值實驗，每個荷載幅值依次進行Near-sfern、 Near-lomap、 Far-chichi、Far-sfern、Mid-loma、Mid-chichi 振動臺實驗，然后進行0.1g白噪聲掃頻，共完成44 個實驗，其中工況1、工況9、工況16、工況23、工況30、工況37、工況44 分別為各階段的白噪聲工況。

2 振動臺實驗結果

2.1 SSI 和SSSI 的結構動力特性

兩組實驗的工況1 的白噪聲激振下的框架頂點與輸入加速度(SSSI 實驗和SSI 實驗分別為A33 和A30 的時程)的傳遞函數如圖6 所示。SSSI實驗中地上結構的一階頻率為9.25 Hz，二階頻率為32.25 Hz；SSI 實驗中地上結構的一階頻率為9.5 Hz，二階頻率為32.5 Hz。相比于底部剛性約束模態實驗結果，SSI 實驗的一階頻率降低，符合土-結構相互作用對結構動力特性的變化規律。同時SSSI 體系中地上結構一階頻率低于SSI 體系，這表明地下空間結構會影響鄰近結構體系的自振頻率。圖7 為兩組實驗不同階段白噪聲掃頻所得的地上結構自振頻率。不同白噪聲工況下，結構的自振頻率有微小的降低，但變化不大，說明模型土具有良好的彈性恢復能力，結合后面的土層動力特性識別結果可認為結構在整個加載過程為彈性。

圖6 框架結構頂部測點傳遞函數Fig. 6 Transfer function of the top point of frame structure

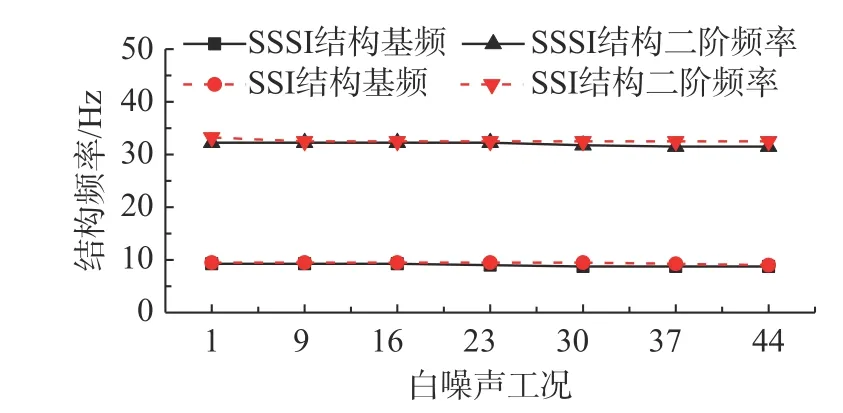
圖7 結構自振頻率Fig. 7 Natural frequency of frame structure

SSSI 實驗中土層表面測點A7 和SSI 實驗中土層表面測點A3 與輸入加速度的傳遞函數如圖8所示。由此可得SSSI 和SSI 體系中場地的基頻分別12.5 Hz 和13.25 Hz。SSSI 體系中場地基頻更小，地上結構自振頻率的變化說明地下空間結構影響了鄰近場地的動力特性并導致鄰近結構動力特性的變化。圖9 為白噪聲下SSSI 實驗和SSI 實驗各工況識別的場地前二階頻率。當輸入波PGA≤0.1g時，場地基頻沒有發生變化，此時場地土狀態基本沒有變化；當PGA 達到和超過0.2g之后，場地基頻隨著PGA 的逐級增高而降低，表明在強震作用下土體進入塑性而導致頻率降低，這也將引起結構體系頻率的降低。

圖8 場地表面測點傳遞函數Fig. 8 Transfer function of site surface

圖9 場地自振頻率Fig. 9 Natural frequency of site

2.2 加速度放大系數

在0.035g輸入地震波下，土層和框架結構加速度放大系數沿高度變化如圖10 所示。與輸入地震波的卓越頻率相比較可知，輸入波Near-sfern 的卓越頻率高于場地基頻，Far-chichi 和Mid-lomap卓越頻率低于場地基頻，另外三條輸入波卓越頻率與場地基頻接近。當Near-sfern、Far-chichi 和Mid-lomap 輸入時框架結構頂端放大系數小于另外三條地震波輸入的加速度放大系數。這表明當輸入波的卓越頻率遠大于或小于結構的基頻，體系的放大系數都比較小，而當卓越頻率與結構的頻率接近時，動力放大系數較大。在不同PGA 輸入下也可以得到類似的結果。

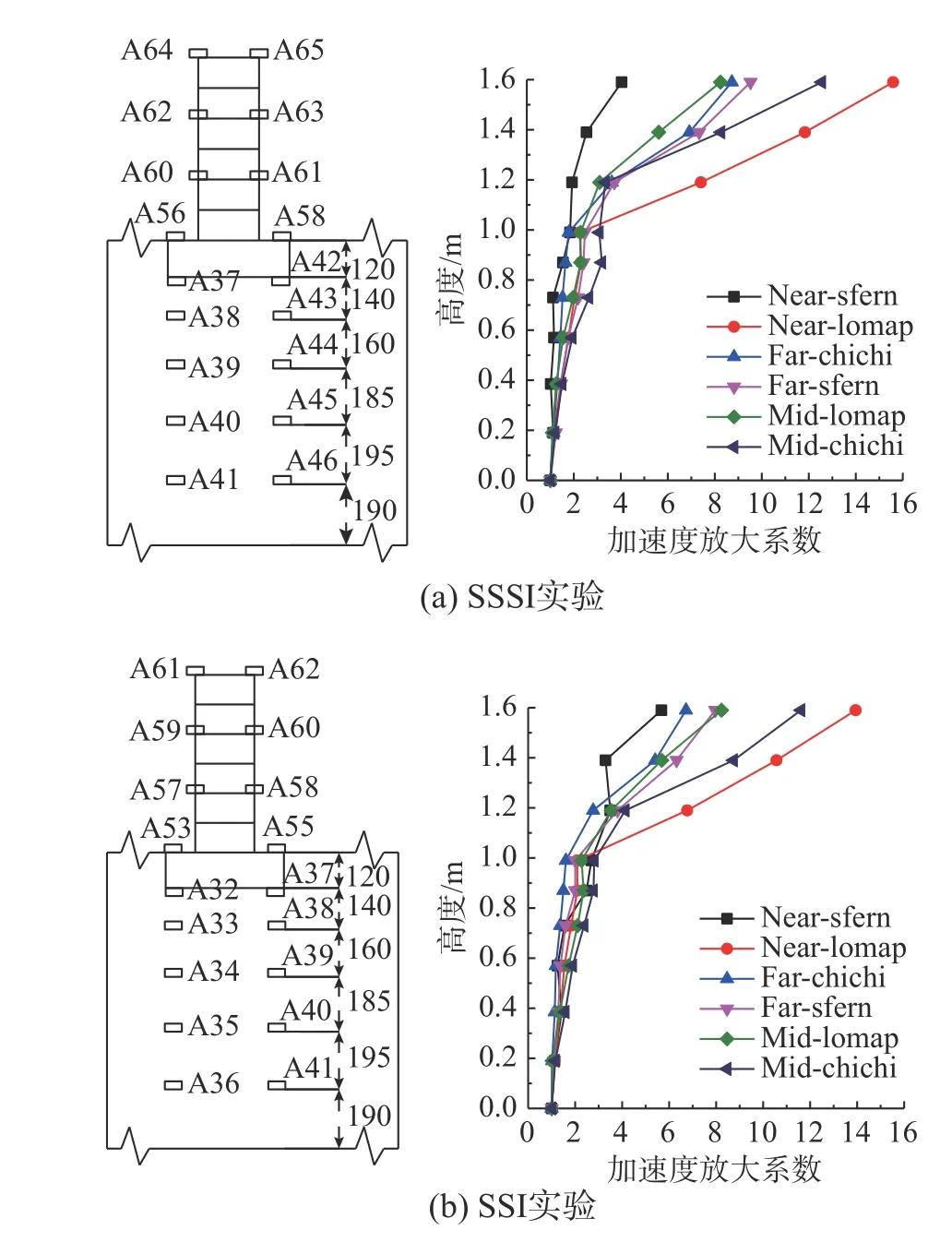
圖10 各地震波輸入下加速度放大系數(PGA=0.035 g)Fig. 10 Acceleration amplification factor under different seismic inputs (PGA=0.035 g)

圖11 為6 條地震波輸入下加速度放大系數平均值沿高度變化分布圖。SSSI 和SSI 放大系數沿高度的變化趨勢是相同的，且加速度放大系數隨著PGA 的增加而減小。這表明地震動輸入越大，由于非線性使土的剪切模量降低、阻尼增大而導致加速度放大系數更小。在PGA=0.035g和0.9g時，SSSI 的放大系數大于SSI 的放大系數；在PGA=0.1g、0.2g、0.4g和0.6g時，SSSI 的放大系數小于SSI 的放大系數，這表明地下空間結構改變了鄰近場地的地面運動，在不同強度地震動輸入下，地下空間結構和鄰近土的非線性程度不完全相同，由此引起的地面運動非常復雜，這將導致地上結構的反應可能大于也可能小于不考慮地下空間結構影響下的地震反應。

圖11 不同PGA 下加速度放大系數Fig. 11 Acceleration amplification factor under different PGAs

3 地上結構加速度反應

3.1 基礎加速度反應

箱型基礎的加速度反應包括平動分量u¨g和搖擺分量θ¨。結合實驗的傳感器測量結果，SSSI 實驗和SSI 實驗基礎的平動和搖擺加速度可表示為：

6 條地震波下箱基u¨g和Hθ¨的放大系數平均值u¨g/a0,max和Hθ¨/a0,max如表1 所示，表1 中H表示地上結構的高度，Hθ¨/u¨g表示平動分量與轉動分量之比。實驗結果表明：對于基礎的平動加速度，兩組實驗的放大系數比較接近，而對于搖擺加速度，SSSI 實驗大于SSI 實驗。地上結構對于土-結構相互作用體系存在慣性相互作用，所以，對于均質土層的SSI體系，箱基的搖擺加速度分量主要是由慣性相互作用引起的。而SSSI 體系鄰近地下空間結構的場地的地面運動不同點存在顯著差異，且存在豎向振動[26]，這導致SSSI 體系中上部結構和土之間不僅存在慣性相互作用，而且，存在運動相互作用，由此，SSSI 體系基礎的搖擺分量大于SSI 體系。

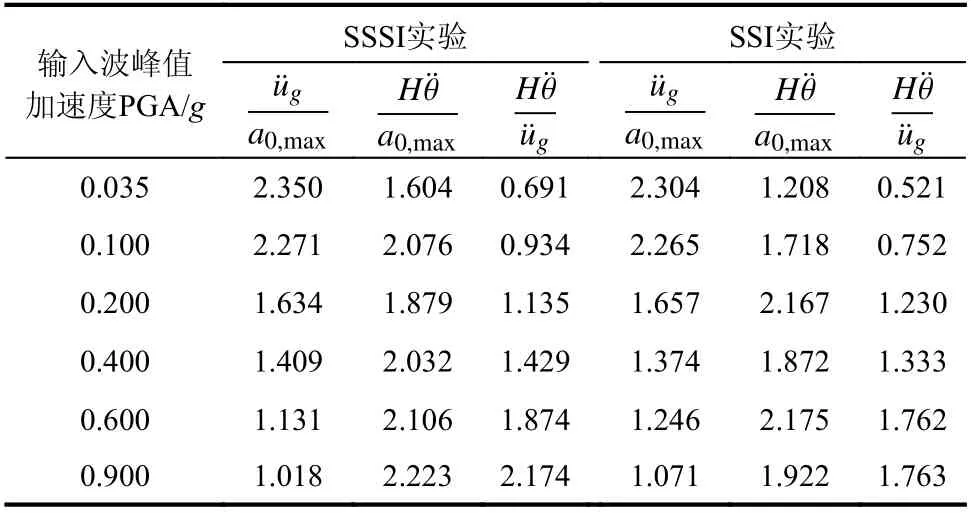
表1 箱基加速度放大系數Table 1 Acceleration amplification factor of box foundation

從Hθ¨/u¨g的角度看，隨著輸入地震波幅值的增加，Hθ¨/u¨g逐漸增大。SSSI 實驗和SSI 實驗的箱基搖擺分量與平動分量之比Hθ¨/u¨g在0.035g時分別為0.691 和0.521，而在0.9g時分別達到了2.174和1.763，這是由于強震作用下土體進入非線性，從土層底部傳播到地表的加速度放大系數減小，所以，平動分量u¨g的放大系數隨著PGA 的增加而減小。在強震導致土體剛度降低時，上部結構的慣性相互作用并沒有降低，由此引起搖擺分量θ¨的放大系數隨著PGA 的增加而增大，這說明在強震作用下，箱基的轉動影響更強。而且SSSI 體系的Hθ¨/u¨g比SSI 的大，因此，對于地下空間結構場地，上部結構將承受更大的搖擺地震動輸入。

3.2 結構頂端加速度反應

由于箱基存在平動和搖擺分量，則圖12 中的地上結構任意高度h處的加速度反應u¨可以表示為[31]：

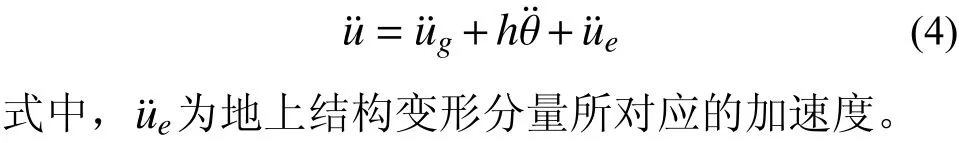
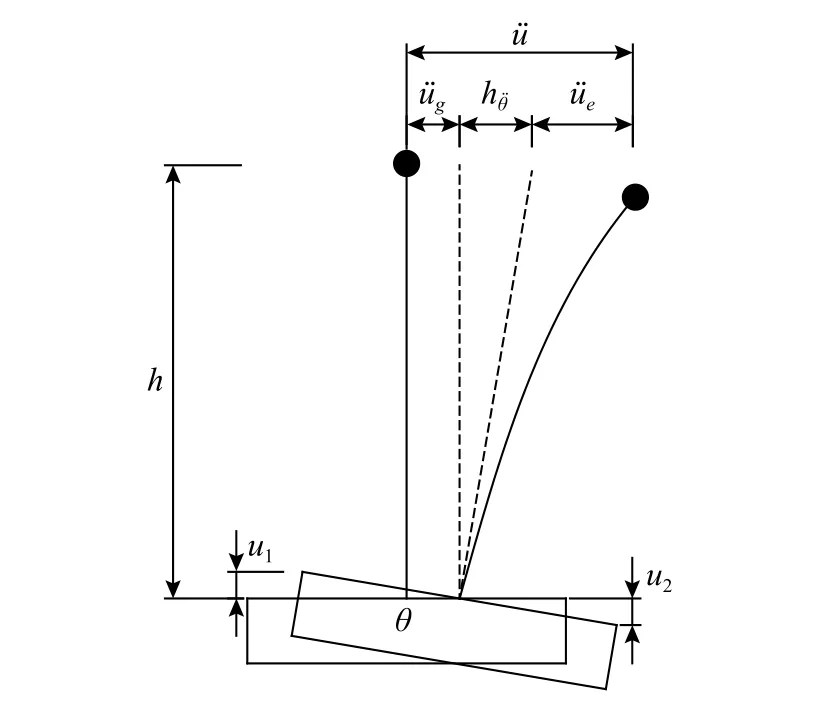
圖12 加速度分量Fig. 12 The components of acceleration

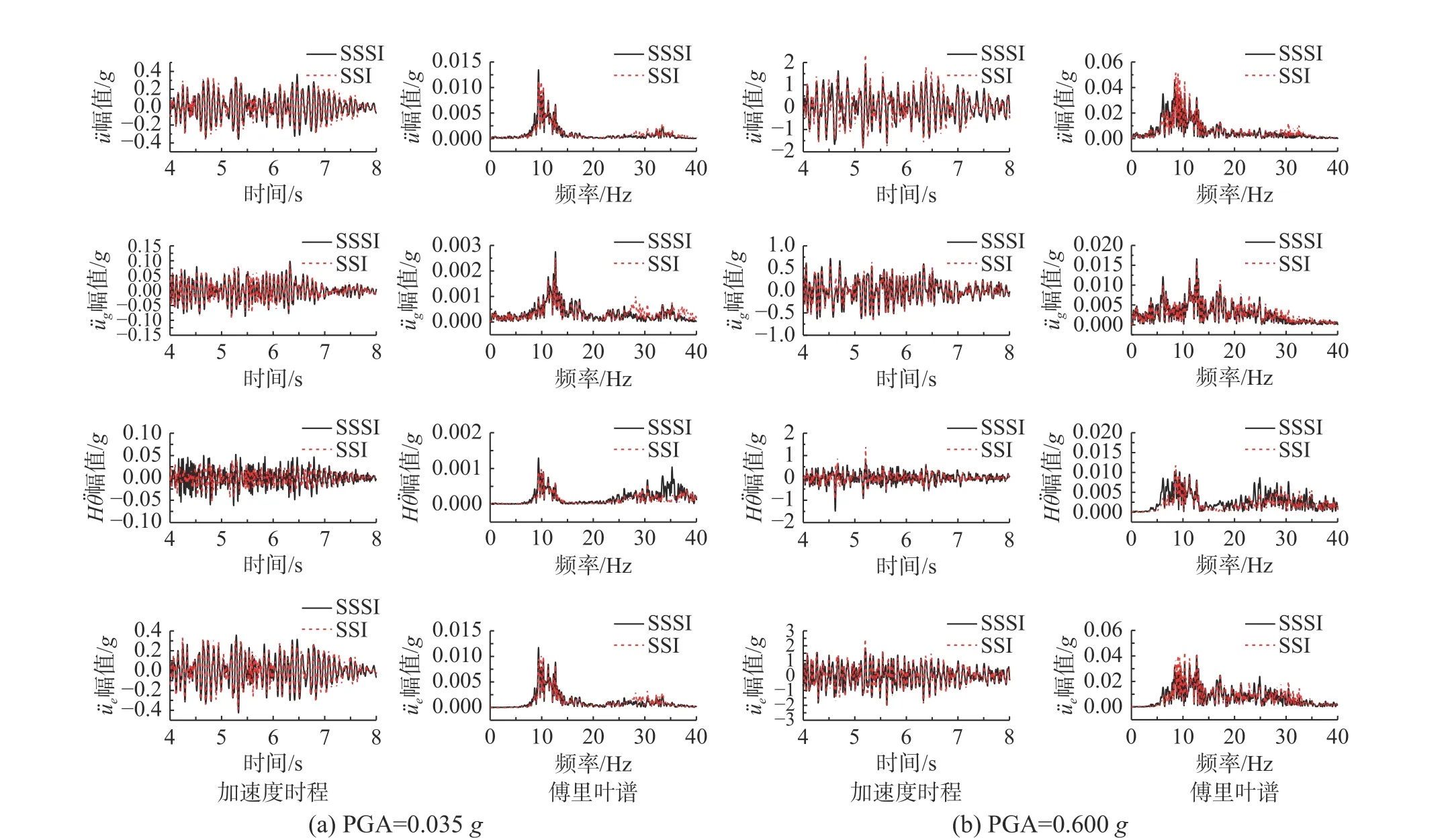
圖13 Far-sfern 地震波下結構頂端加速度時程及傅里葉譜Fig. 13 Acceleration time history and Fourier spectrum of the top of frame structure under wave far-sfern

為進一步分析SSSI 體系變形分量的增加效果，令re=βu¨e1/βu¨e2表示SSSI 和SSI 體系中結構頂端變形加速度分量放大系數的比值。表2 為各工況下re的計算結果。由于地下空間結構的局部場地效應影響，re的值可能大于1 也可能小于1，地下空間結構對增強地上結構反應的趨勢具有不確定性。6 條輸入波6 個輸入加速度幅值下，re的值最大可達1.267，最小為0.669。由于未來地震波的不確定性，為保證實際工程結構的抗震安全性，應考慮地下空間結構對鄰近結構的影響。

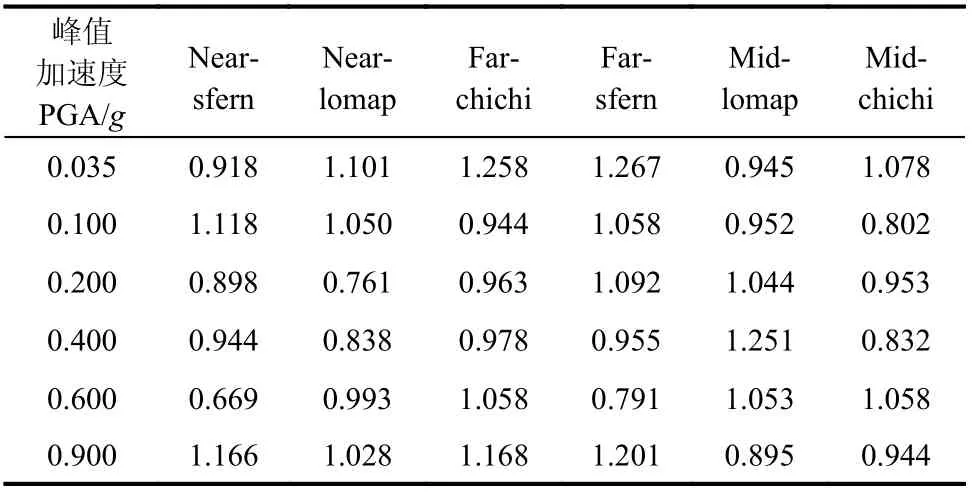
表2 結構頂端變形加速度放大系數比值reTable 2 Ratio of deformation component of acceleration amplification factor at the top of structure re

4 結論

為研究地下空間結構-土-地上結構動力相互作用及其地震反應，以相互鄰近的大型地下空間結構和地上框架結構為原型，按照幾何相似比為1∶30 進行了實驗模型設計和制作，根據實驗結果可得出以下結論：

(1) SSSI 體系的動力特性受地下空間結構影響，實驗中SSSI 體系的地上結構頻率和場地基頻均小于SSI 體系，即地下空間結構影響鄰近場地的動力特性，進而影響鄰近結構的動力特性。

(2) 輸入地震波的頻譜特性顯著影響結構的地震反應，當輸入波的卓越頻率遠大于或小于結構的基頻，體系的放大系數較小，而當卓越頻率與結構的頻率接近時，動力放大系數較大，這一點對SSSI 和SSI 是相同的，且加速度放大系數隨輸入地震波峰值的增加而降低。

(3) 在SSSI 體系的箱基存在更明顯的運動相互作用而導致SSSI 體系的箱基搖擺運動顯著大于SSI 體系。隨著輸入地震波峰值的增加，SSSI 體系的箱基搖擺運動增加幅度更大。SSSI 實驗和SSI 實驗的箱基搖擺分量與平動分量之比Hθ¨/u¨g在PGA=0.9g時分別達到了2.174 和1.763。

(4) 箱基的平動加速度、搖擺加速度和結構變形加速度分量的峰值并不同步。SSSI 體系箱基搖擺分量增大可能導致上部結構總加速度和變形分量增大。SSSI 體系的結構變形反應最大可達到SSI 體系變形反應的1.267 倍。由于未來地震輸入的不確定性，應考慮地下空間結構對鄰近地上結構的影響，以提高上部結構的抗震安全性。