用于移動式供電的永磁同步發電機優化設計

曾繁琦,卜建國,袁曉靜,王旭平,張 澤

(1.火箭軍工程大學 作戰保障學院， 西安 710025； 2.陸軍軍事交通學院 軍用車輛工程系， 天津 300161)

1 引言

軍事裝備移動式發電車不僅是滿足武器裝備電力供應的能量保障平臺，還是執行作戰任務的軍用車輛裝備，逐漸成為各種武器裝備的最佳承載平臺和應用載體。發電車以供電作為主要功能，其發電指標的優劣直接影響上裝武器裝備能否正常使用，對戰爭作戰態勢變化起了決定作用，供電系統發電指標的提升已成為發揮武器裝備性能潛力的關鍵因素。發電指標取決于電機的供電性能和電壓調節裝置的調壓能力，而電機的供電性能也會受到電機設計過程中結構參數選取的影響，但完全依賴在電機上增加基于電力電子變換的電壓調節器的方法來改善整車的供電品質會導致整車投入成本增加，而對于大功率電機甚至會增加調壓裝置的負擔，同樣會增加控制成本。因此，開展電機優化設計研究非常必要。

2 供電系統總體布置方案

軍事裝備移動式供電系統是基于傳統軍用車輛底盤系統開發而成，通過加裝電機實現移動式供電功能，為車載武器裝備提供電力保障。軍事裝備移動式發電車底盤布置方案如圖1所示，該方案采用電機直接與發動機曲軸相連的方式，電機通過AC/DC轉換器、DC/DC轉換器分別與高低壓負載以及蓄電池組相連，其優點在于：

1) 系統繼承性好。在開發軍事裝備移動式供電系統時應盡量減少傳統軍用車輛底盤結構變化，電機布置于發動機離合器之間保持了原發動機、變速器、驅動后橋等結構不變，對車輛改動不大的情況下實現駐車發電功能，具有良好的繼承性。

2) 實現駐車發電功能。車輛處于停駛狀態時，供電系統控制發動機帶動電機運轉，進行駐車發電，在軍隊作戰和演習時為作戰、通訊以及生活設施等裝備提供移動式電力保障。

3) 發電效率高。電機和發動機曲軸直接相連，二者之間無其他傳動部件，降低了機械傳動損耗，提高了發電效率。

4) 能夠實現減重。電機直接替換原有飛輪，可以充分利用電機轉子轉動慣量，達到減重的效果，且隨著車輛用電功率的增大，其優勢會越來越明顯。

供電品質是衡量電力供應平臺優劣的一項關鍵指標，軍事裝備移動式發電系統的供電品質取決于電機的供電性能和整流器或逆變器的電壓調節能力，而電機的供電性能也會受到電機設計過程中結構參數選取的影響。因此，從動力系統設計角度出發對系統供電單元進行優化設計可以改善系統的供電品質，那么合理的電機結構設計對于改善發電指標就顯得尤為重要。

圖1 軍事裝備移動式發電車總體布置方案示意圖Fig.1 The general layout scheme of military equipment mobile power generation vehicle

3 電機優化設計方法研究現狀

電機設計需要確定一定數量的尺寸和材料參數，是一個多變量、多約束、非線性的多目標數學問題，目前國內外很多學者已經對電機優化設計方法進行了大量研究。

1) 基于磁路法的優化方法

Bazghaleh等采用傳統的磁路法和有限元法對永磁電機進行優化設計[1-3]，但精度低、計算量大。因此，為了提高精度與減少計算量，逐漸形成采用有限元法與局部或全局優化算法相結合的優化方法替代傳統方法的研究趨勢。

2) 田口試驗方法

Srikomkham等針對永磁分壓電容式單相感應電機轉子設計問題提出了一種優化方案，以起動轉矩和電機效率為優化目標，采用田口(Taguchi)試驗方法與有限元相結合的方法進行多參數優化設計，并計算分析了起動轉矩和電機效率[4]。

胡巖等針對航空用高速永磁發電機電磁設計問題，以發電效率為優化目標，采用Taguchi法與有限元相結合的方法，得到滿足發電機性能的最佳設計組合參數[5]。

劉彥呈等以無人水下航行器推進用內置式永磁同步電機為研究對象，采用有限元法確認了各優化參數及取值范圍，以效率、永磁體用量、轉矩脈動為優化目標，通過Taguchi法對電機進行優化設計，得出電機多目標優化設計的方案[6]。

Yang等采用結構計算的方法對開關磁阻電機進行了設計，以效率為優化目標，通過Taguchi法對電機效率進行優化設計，為設計出更高效率的開關磁阻電機提供參考[7]。

Taguchi方法是日本著名統計學家田口玄一在研究2水平和3水平正交數組的基礎上得到的，通過建立正交試驗實現優化設計獲得局部最優解，但是無法實現全局最優。

3) 智能優化算法

Sadeghi等針對傳統磁滯電機低效率、低功率因數的缺點，將無鐵芯雙圓盤結構引入到電機設計中，初步提高了電機效率，采用遺傳算法解決了該新型磁滯電機的效率優化問題，輸出功率和效率的理論值與實測值吻合較好，驗證了算法的有效性[8]。

石書琪等將遺傳算法應用到雙饋風力發電機優化設計當中，全局尋求電機的最優成本[9]。

金亮等針對傳統優化方法的不足，將遺傳算法同有限元相結合，以感應電壓和磁通密度作為優化目標，完成永磁同步發電機的優化[10]。

Thejaswini等將遺傳算法應用到風力渦輪發電機優化設計中，分析了不同工況下的電機性能，遺傳算法的應用有助于選擇更好的發電機設計參數[11]。

Razik等介紹了一種利用輸出誤差辨識感應電機參數的方法，證明了遺傳算法和擬牛頓法是識別感應電機參數的有力工具，2種優化算法對于線性和非線性模型均適用，驗證了2種算法的有效性[12]。

郎旭初等在采用等效磁路的方法對汽車用永磁發電機進行初步設計的基礎上，以電機效率為優化目標，運用擬牛頓法和模式搜索法對電機進行了優化，得到了發電機優化變量和性能參數的優化結果[13]。

遺傳算法、擬牛頓法和模式搜索法已經是應用比較成熟的優化算法，遺傳算法能有效地避免優化過程陷入局部最優，搜尋到全局最優解，但它仍然具有收斂速度較慢、后期優化效率較低等缺點；擬牛頓法迭代次數較多、計算量較大；而模式搜索法對起始點比較敏感，對于某些起始點只能得到局部最優點；同時與電機優化相結合的貪心算法、爬山算法等優化算法也容易使得優化過程陷入局部最優解。

4) 解析優化方法

Shiri等采用解析優化方法對普通復合次級直線電機的初級和次級同時進行了優化設計，使得電機質量及其性能均達到比較滿意的結果[14]，但對于有些復雜的非線性優化問題，解析優化方法是不適用的。

5) 基于代理模型的優化方法

近年來，基于代理模型的多目標優化方法被引入到電機的優化設計中，從而提高了優化效率，已經有研究學者通過大量的仿真試驗和實際電磁設計對其可靠性進行了驗證。Zhang等將Kriging代理模型引入到多目標優化設計中，Kriging方法擬合得到的代理模型具有全局和局部的統計特性，擬合精度較高[15-17]，從而使得多目標優化方法得到進一步發展，即代理模型與隨機優化算法相結合成為近年來電機優化問題研究的新趨勢。

Zhang等將優化拉丁超立方設計方法引入到Kriging模型和傳統遺傳算法相結合的優化算法中，以減小永磁直線同步電機的邊端定位力為目標，對電機參數進行優化設計，實現了良好的優化效果[15]。

Kim等采用基于傳統拉丁超立方設計方法的Kriging模型和傳統遺傳算法得到了內置式永磁同步電動機轉子的最佳形狀，在減小齒槽轉矩的同時，實現了寬轉速范圍[16]。

湯春球等均采用了傳統拉丁超立方設計方法、Kriging模型以及全局優化算法相結合的優化方式，被優化對象的性能較優化前顯著提高，驗證了所提出的性能優化方法是有效的[18-19]。上述研究雖然得到了令人滿意的優化結果，但是由于一些傳統方法的局限性，優化過程不能快速高效的進行，因此優化方法仍有待進一步改進。

綜上所述，傳統的電機優化設計方法存在一定不足，且優化過程中未考慮對發電指標的優化，優化方法與發電性能仍具有改進空間。

4 電機優化設計仿真研究

4.1 電機模型的建立

本文研究的永磁同步發電機截面示意圖如圖2。由于徑向結構在性能方面要優于切向結構，因此選擇內轉子內置式徑向磁路結構作為電機結構，并且為了減少電機雜散損耗，定子繞組形式采用分布式單層短節距的星形接法。

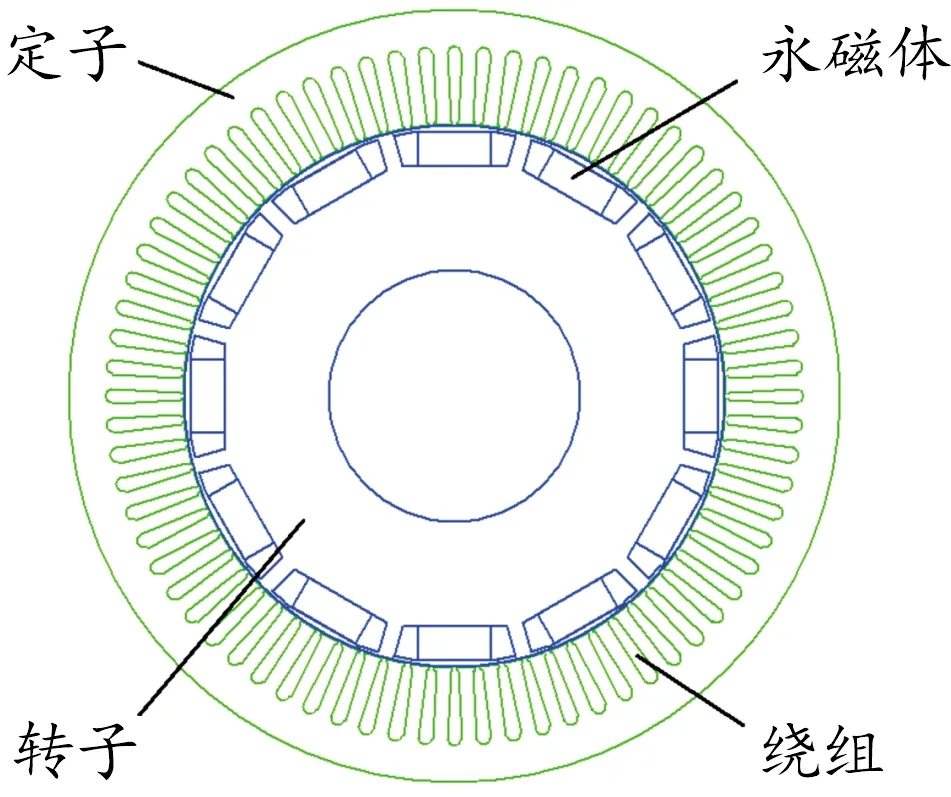
圖2 電機整體結構示意圖Fig.2 The structural diagram of whole generator

電機的1/12結構如圖3所示，選取的結構設計參數分別為槽口寬度bs0、氣隙長度δ、永磁體厚度hm、永磁體寬度bm、磁橋寬度bb、永磁體間距br和軸向長度L。

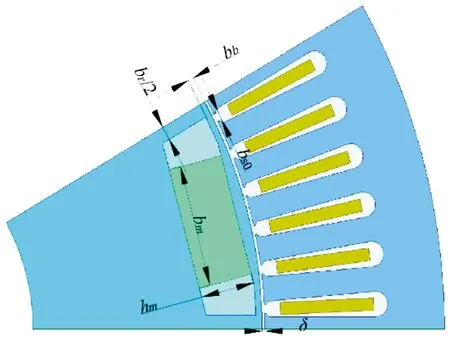
圖3 電機1/12結構示意圖Fig.3 The structural diagram of one-twelfth generator

選取的電機性能參數分別為電壓調整率ΔU、空載電動勢波形畸變率kU和電機效率η，作為電機的3個重要發電指標參數，其大小直接影響著電機的發電性能。3個參數的表達式分別如式(1)、式(2)、式(3)所示。

(1)

式中：f為頻率；N為電樞繞組每相串聯匝數；K為繞組因數；Φ為每極空載氣隙磁通；KΦ為氣隙磁通波形系數；U為輸出電壓；UN為額定相電壓有效值。

電壓調整率是電機工作在發電模式時的重要性能指標之一。在實際應用中，過高的電壓調整率將對用電設備的運行產生較大影響，理想的情況是電壓調整率盡可能小，因此有必要選擇適當的電機參數對電機進行周密設計。電機制造成型后，永磁體產生的磁場難以調節導致輸出電壓很難控制[20-21]，然而目前采用的調壓或穩壓的方法是在電機上加裝電力電子變換調壓器，但這種方式存在結構復雜、成本高等缺點，特別是對于需要大范圍調壓的高功率電機，降低電機的電壓調整率可以減輕其電壓調節設備的負擔。因此，如何減小電壓調整率是電機設計的重要問題之一。

(2)

式中：Uv為電壓中v次諧波的有效值；U1為電壓的基波有效值。

電壓波形畸變率決定了發電機供電品質的優劣，工業生產中對同步發電機的電動勢波形正弦性具有嚴格要求。內置式永磁同步發電機中，由于諧波的影響空載電動勢波形也不完全呈現正弦性，這會影響輸出電壓的穩定性。因此，很有必要減少電機空載電動勢的諧波，通過改變結構參數調整電動勢的波形[22-23]，以達到電壓波形正弦性變好的目的[24-25]。

(3)

式中：∑p為發電機總損耗；P為發電機輸出功率。

在永磁同步電機設計中電機性能的重要指標包括輸出功率、效率和功率密度等，因此提高電機的效率以及增大輸出功率可以改善電機的性能。

根據電機結構設計參數建立二維有限元模型，通過對電機進行空載磁場分析，可以得到電機空載磁場分布，由此了解電機各部分磁場的飽和情況，并判斷磁路設計是否合理。本文設計的電機磁力線分布如圖4所示。

圖4 磁力線分布示意圖Fig.4 The distribution of magnetic field line

永磁體產生的磁通包括主磁通和漏磁通，主磁通通過定轉子之間的氣隙進行能量轉換，漏磁通的磁感線通過漏磁路閉合，主磁路和漏磁路并聯形成每對磁極的磁路。從圖4磁力線分布圖可以看出漏磁通較小，因此從漏磁的角度看設計是滿足要求的。

4.2 代理模型方法研究

電機是一個多變量、非線性的物理模型，對原模型直接進行優化會降低優化效率，因此，本文采用代理模型方法尋找電機的近似模型，為優化設計奠定基礎。

代理模型方法是通過數學模型的方法逼近一組輸入變量與輸出變量的方法。20世紀70年代，L.A.Schmit等在結構設計優化中首次采用代理模型的方法，提高了優化算法的效率，使其在工程領域中的應用效果也逐漸凸顯，其具體流程如圖5所示。目前常用的代理模型方法包括多項式回歸模型、神經網絡模型[26-27]、Kriging模型等。

圖5 代理模型流程框圖Fig.5 The process of surrogate model

為了驗證上述3種代理模型對非線性問題的近似程度，本文從非線性函數式(4)中選取25個樣本點，分別采用多項式回歸模型、神經網絡模型、Kriging模型3種方法進行擬合[28]，擬合曲線如圖6。

f(x)=3sin(2x)+2x2cos(5x+6)

(4)

圖6 不同代理模型方法的擬合曲線Fig.6 The fitting curves of different surrogate model methods

從圖6中可以看出，多項式回歸模型的擬合精度最差，無法跟蹤原函數；BP神經網絡模型的擬合精度比多項式回歸模型有所提高，但局部精度仍然不高；Kriging模型基本與原函數重合，擬合精度最高。因此，本文選取Kriging模型作為擬合代理模型的方法。

4.3 多目標優化設計

以電壓調整率ΔU、空載電動勢波形畸變率kU和電機效率η作為優化目標建立優化模型：

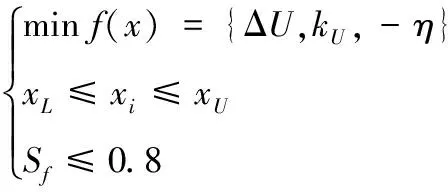
(5)

式中：f(x)為目標函數；x=[bs0,δ,hm,bm,bb,br,L]為優化變量；xU和xL分別為優化變量的最大值和最小值；Sf為槽滿率。

在運用最大投影試驗設計方法[29-30]進行樣本數據采集的基礎上，本文采用基于Kriging代理模型的NSGA-Ⅱ算法[29,31]對永磁同步發電機進行優化設計。從如表1所示優化結果的Pareto最優解集中選取3組優化方案。方案1側重優化ΔU和η，方案2兼顧了3個目標函數，方案3側重優化kU。發電機不同的功率等級與相應發電指標類型對應著不同的參數指標，根據電機設計電氣指標要求與不同的優化目的，可以制定不同的優化策略，從而得到滿足供電需求的優化設計結果。從表1可以看出，3組方案的目標函數值均優于初始方案，說明了所提出優化設計方法是有效的。

5 最優方案發電指標評價

軍事裝備移動式發電車從廣義上可以稱為陸用內燃機移動電站，則其電氣指標就需要滿足移動電站通用規范要求，而發電車的供電品質又會受到電機供電性能的影響，因此本文擬參考《GJB 235A—1997軍用交流移動電站通用規范》中規定的電氣性能指標對電機最優設計方案的發電指標進行評價。該規范適用于0.5～500 kW的軍用移動電站，對電站指標類別、電壓調整率、電壓波形畸變率進行了詳細規定，其規定指標如表2所示。

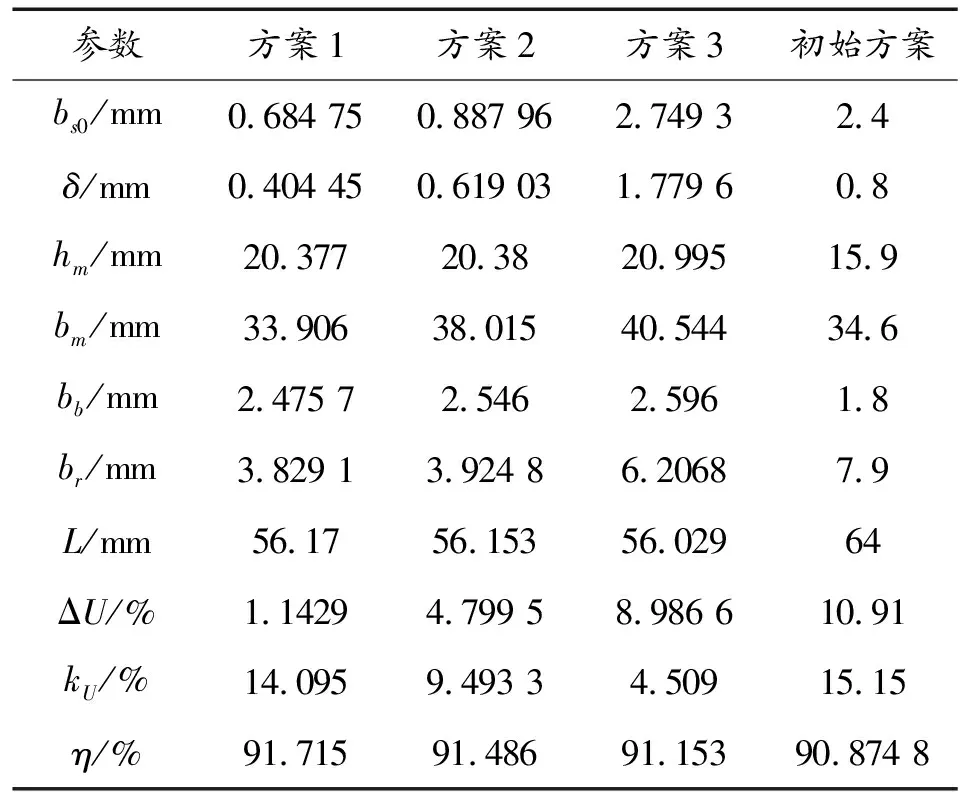
表1 優化結果

表2 電氣規定指標

從表1中初始方案的發電指標與表2中電氣指標對比可以看出，電機初始方案的電氣性能指標不滿足移動電站通用規范要求，說明通過電機優化設計進而優化發電指標是很有必要的；從表1中3組最優方案發電指標與表2中電氣指標對比可以看出，在電機保持高效率的情況下，3組最優方案的電氣指標分別滿足了不同等級電站的要求。其中，方案3以犧牲掉一部分電壓調整率為代價，電壓波形畸變率達到了最優標準；方案2滿足了Ⅳ類電站的標準，而方案1達到了Ⅰ類或者Ⅱ類電站的標準，電站指標類別優于其他2種方案。

綜上所述，優化后的設計方案可以滿足Ⅰ類電站要求，優化效果明顯，在改善了電機供電性能的同時，也減輕了電壓調節設備以及整車系統的負擔，對整車發電指標起到了優化的作用，可以滿足對供電品質要求更高的武器裝備等用電設備的用電需求，這對提升軍事裝備移動式發電車供電品質具有重要軍事意義。

6 結論

1) 提出了一種改進的組合優化策略優化了電機發電指標，從電機模型的空載磁場分析結果看出設計滿足要求；選取的Kriging代理模型對于解決非線性問題具有較強的預測能力，其擬合精度具有明顯優勢。

2) 采用基于Kriging代理模型的NSGA-Ⅱ多目標優化算法對電機性能指標進行多目標優化，優化算法準確，軍事裝備移動式發電車的發電品質也得到了改善。

3) 最優方案可以滿足Ⅰ類電站要求，對發電指標起到了較好的優化效果，可以滿足對供電品質要求更高的武器裝備等用電設備的用電需求，對改善軍事裝備移動式發電車供電品質具有重要意義。

4) 本文提出的優化組合策略可以大大降低電機設計過程中的有限元計算成本，為更高功率等級的電機設計奠定基礎，但要同時考慮實際制造工藝與使用情況。