考慮地震動水力的高速鐵路跨海斜拉橋行車安全性研究
雷虎軍,劉 偉,孫昱坤
(福建工程學院 土木工程學院,福建 福州 350118)
近年來,隨著我國高速鐵路建設從陸地逐漸延伸到海洋,跨海橋梁已成為高速鐵路線路的重要組成部分,尤其是斜拉橋結構,跨越能力強、剛度大,是高速鐵路跨海橋梁的首選,例如正在建設中的福廈高鐵泉州灣跨海大橋、安海灣跨海大橋都采用了斜拉橋結構[1]。我國東部和東南部沿海位于東南沿海地震帶,且毗鄰臺灣海峽地震帶,地震區密集。歷史上在泉州、晉江、惠安等海域都發生過強震,給該地區造成了巨大的人員傷亡和經濟損失。因此,沿海的高速鐵路跨海斜拉橋及橋上列車面臨地震的嚴重威脅。
關于地震引起的車橋耦合振動問題,近年來從簡化的車輛模型到復雜車輛模型、從輪軌密貼假設到新型輪軌關系、從地震一致激勵到多點激勵,眾多學者進行了系統研究,成果顯著[2-6]。其中,對于鐵路斜拉橋,熊建珍等[7]以天興洲斜拉橋方案為例,分別針對貨物列車、中速旅客列車和高速旅客列車進行了地震-車-橋仿真計算。韓艷等[8]通過建立地震作用下的列車-橋梁空間耦合振動模型,對列車通過某斜拉橋的全過程進行了仿真計算。朱志輝等[9]以某獨塔斜拉橋為研究對象,采用等效荷載法計算車橋系統的地震響應,研究了橋上列車的行車安全性。相比普通鐵路斜拉橋,高速鐵路跨海斜拉橋面臨深水環境,一旦發生地震,在橋梁下部結構會產生附加動水力,眾多研究表明地震引起的附加動水力會改變結構的自振頻率,對橋梁的動力響應影響顯著[10-12]。然而,地震附加動水力對斜拉橋-列車系統動力響應的影響究竟如何,目前鮮有報道。
因此,要研究地震作用下高速鐵路跨海斜拉橋的行車安全性,首先應解決車橋系統中地震動水力的計算問題。黃信等[13]基于輻射波浪理論,推導了深水橋墩的地震動水力計算公式,探討了水底柔性反射邊界的影響。王丕光等[14]推導了橢圓柱體地震動水力的精確解析解,并進行了驗證。杜修力等[15]基于不可壓縮水體輻射理論得到了圓形橋墩地震動水力的解析解,探討了剛性柱法、Morison法和基頻近似法3種簡化方法的計算精度,研究表明剛性柱法的誤差最小。郭婕等[16]從頻域傳遞函數的角度探討了上述3種地震動水力近似求解法的計算精度,并推薦使用剛性柱法。由于地震-列車-橋梁耦合系統模型規模大、非線性強,在系統中采用簡化方法來模擬水-結構間的相互作用、計算地震動水力較為合理。
本文在以往研究的基礎上[17],基于原有的地震-車-軌-橋耦合振動分析程序Ttbsas,采用剛性柱法模擬下部結構的地震動水力,并將其轉換為節點附加質量,建立了考慮地震動水力的地震-車-軌-深水橋梁耦合振動模型,同時作為對比建立了不考慮地震動水力的耦合振動模型。以某跨海斜拉橋為例,通過輸入3條實測地震波進行仿真計算,研究了地震動水力對車-軌-橋系統動力響應的影響,在此基礎上分析了橋上高速列車的行車安全性。本文的研究成果可為高速鐵路跨海斜拉橋的設計提供理論支持。
1 地震動水力簡化計算方法
如圖1所示,假設底部固定的懸臂圓柱體位于理想無黏性不可壓縮水體中,水平地震波作用于柱底,忽略水體表面的自由波,則其運動方程為

圖1 水平地震力作用下的懸臂圓柱體
(1)

根據水體的控制方程和上述邊界條件,即可推導該圓柱體在深度z處的精確地震動水力解[18]為
(2)

由此可知,精確的地震動水力是結構變形的函數。采用有限元法進行數值求解,則式(1)可采用向量和矩陣表達為
(3)
式中:
(4)
其中,Mw為動水力等效質量矩陣;N為單元的形函數。
將式(3)帶入式(1)即可得到考慮地震動水力作用的結構運動方程為
(5)
采用剛性柱法進行簡化計算[18]。在剛性柱法中,假設結構為剛體,則Mw中的項可簡化為
(6)
Wang等[19]為便于工程應用,將式(6)中的級數求和進行了擬合,進一步簡化為
(7)
(8)
式中:L=2R/H為圓柱體直徑與水深之比。
將式(7)、式(8)計算的節點附加質量項帶入式(5),即可求解考慮地震動水力作用的結構運動方程。由于上述推導是基于懸臂圓柱體,而實際工程中,矩形承臺或橋墩應用非常廣泛。賴偉[20]通過試驗并采用最小二乘法擬合,得到了單位高度矩形截面的動水力附加質量與圓形截面動水力附加質量的等效換算系數為
(9)
式中:K為矩形截面換算系數,適用于0.1≤D/B≤10;D為矩形截面垂直于水流方向的寬度;B為平行于水流方向的寬度。
根據式(7)~式(9)即可計算圓形和矩形截面的動水力附加質量。
2 地震-車-軌-深水橋梁耦合振動模型
地震作用下的車-軌-深水橋梁耦合振動模型是在原有地震-車-軌-橋動力模型的基礎上考慮地震時水與橋梁下部結構的相互作用形成的。因此,該模型包含原有的車輛、軌道、橋梁、輪軌關系、橋軌關系和地震力邊界等模型以及新增的水-結構相互作用模型,見圖2。

圖2 地震-車-軌-深水橋梁耦合振動模型
在以往研究中基于新型輪軌關系假設和橋軌間的靜力平衡條件建立了非一致地震激勵下的車-軌-橋空間耦合振動模型,同時利用Compaq Visual Fortran平臺編制了列車-軌道-橋梁-地震仿真分析程序Ttbsas[21],可以實現地震作用下任意橋型的車橋耦合振動仿真計算。基于此,將水-結構間的相互作用采用前述剛性柱法進行簡化考慮,即可建立起地震作用下的車-軌-深水橋梁耦合振動模型,其運動方程可統一表達為
(10)

由式(3)~式(9)計算,聯立求解方程式(10)即可得到地震作用下考慮地震動水力的深水橋梁-列車系統的耦合振動響應。
3 算例
3.1 計算參數
以某主跨400 m的雙塔雙索面半漂浮體系跨海斜拉橋為例進行仿真計算。橋梁全長940 m,跨度布置為(70+70+130+400+130+70+70) m,結構總體布置見圖3。其中,橋上軌道采用CRTSⅡ型板式無砟軌道;主梁采用混凝土橋面板加槽型鋼箱梁的疊合梁,寬16 m、高4.5 m;橋塔采用鉆石型混凝土塔,塔高169.3 m,橋塔承臺為矩形截面,尺寸為40 m×25 m,橋塔群樁基礎的樁柱為圓形截面,直徑為2.8 m;斜拉索采用鍍鋅平行鋼絲索,按扇形對稱布置72對。二期恒載取133.4 kN/m。

圖3 主跨400 m高速鐵路跨海斜拉橋(單位:m)
采用Midas Civil 2019分別建立兩種斜拉橋有限元模型,即:考慮地震動水力(模型1)、不考慮地震動水力(模型2)。在模型1中,橋梁的局部沖刷線以上至最高水位線以下采用剛性柱法計算承臺、樁柱的地震動水力附加質量,主塔的動水力附加質量計算結果見表1。

表1 動水力附加質量計算結果
采用子空間迭代法分別計算兩種模型的自振特性,其自振頻率對比見圖4。由圖4可知,兩種模型的基頻相同,均為0.145 Hz,且前10階自振頻率相差很小;考慮地震動水力后斜拉橋高階模態的自振頻率明顯低于不考慮地震動水力時,且模態40~100為橋塔底部群樁的振型,這是由于考慮地震動水力后群樁的剛度不變而質量增大了。由此可見,地震動水力會顯著影響斜拉橋的頻率分布。將建立的兩種斜拉橋模型導入Ttbsas程序,即可得到車橋計算的橋梁模型。

圖4 兩種模型自振頻率對比
根據場地條件(Tg=0.45 s,設計地震PGA為0.15g),在太平洋地震工程研究中心選取3條典型地震記錄作為輸入,主要參數和加速度分別見表2、圖5。
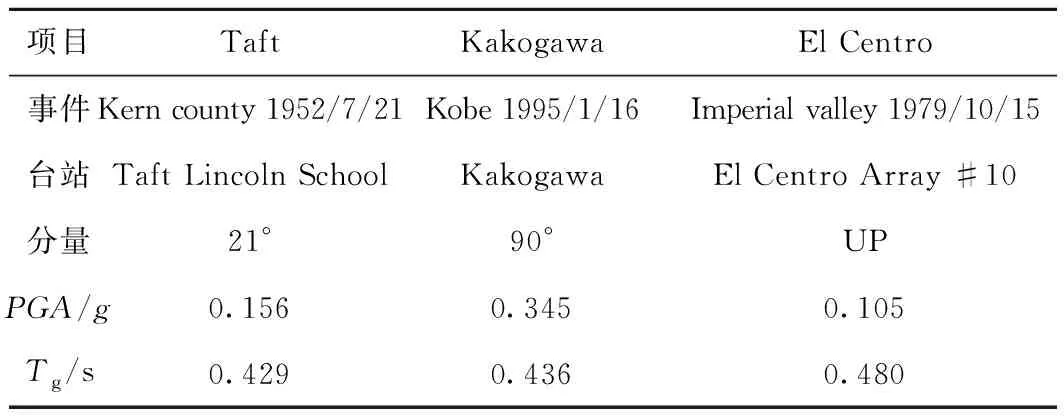
表2 地震波信息

圖5 地震波加速度時程
3.2 地震動水力的影響分析
根據建立的兩種斜拉橋模型,首先輸入Taft地震波,考察CRH3高速列車以時速350 km/h過橋時地震動水力對車橋系統動力響應的影響。橫向和豎向地震動峰值加速度分別取0.1g和0.065g,假設地震發生時刻與列車上橋時刻相同。斜拉橋主梁跨中的橫向位移和豎向位移時程見圖6,主梁跨中斷面左側鋼軌的橫向位移和豎向位移見圖7,列車的脫軌系數、輪重減載率和輪對橫向力時程見圖8。

圖6 主梁跨中位移時程對比

圖7 主梁跨中左側鋼軌位移時程對比
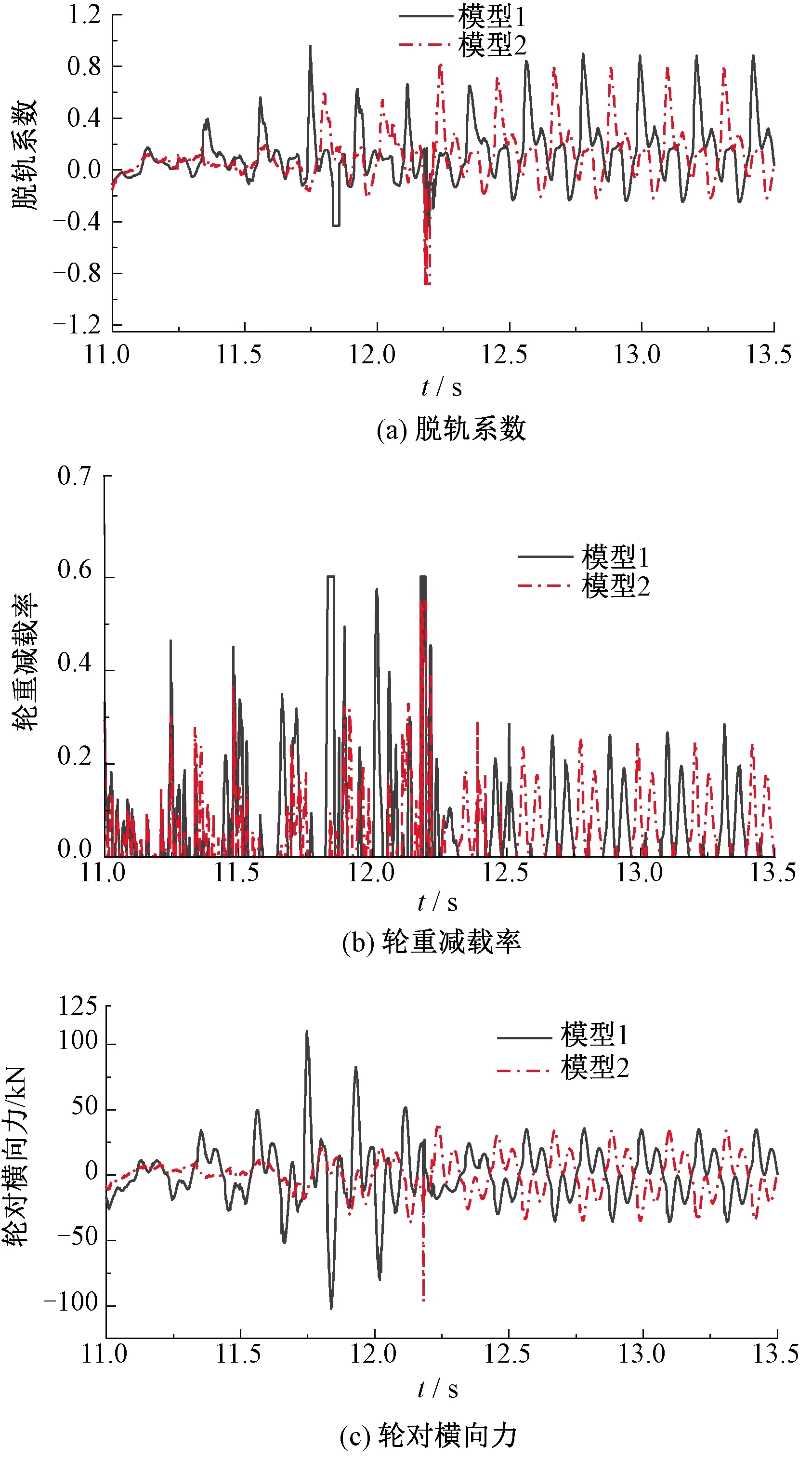
圖8 列車行車安全性指標時程對比
由圖6可知,考慮地震動水力后斜拉橋主梁跨中的橫向位移時程與不考慮時波形相似,但幅值不同,且考慮地震動水力后的幅值大于不考慮時。而對于斜拉橋主梁跨中的豎向位移,兩種模型的差值趨于0。由此可見,地震動水力對斜拉橋主梁的橫向位移影響較大,而對其豎向位移幾乎無影響。
由圖7可知,地震動水力對橋上鋼軌的橫向位移影響顯著,且考慮動水力后,橋上鋼軌的橫向位移幅值大幅增加。此外,地震動水力對橋上鋼軌的豎向位移影響不大,兩種模型計算的鋼軌豎向位移時程相差很小。
由圖8可知,考慮地震動水力后輪軌間的脫軌系數、輪重減載率和輪對橫向力的波形和幅值均差異較大,且考慮地震動水力后的幅值均大于不考慮時。由此可見,對于高速鐵路跨海斜拉橋,不考慮地震動水力會低估列車過橋的行車安全性指標。
按照同樣的方法對Kakogawa、El Centro地震波進行規格化處理,進一步考察不同地震波作用下地震動水力對車橋系統動力響應的影響。兩種斜拉橋模型主梁跨中的動力響應幅值對比見表3,列車的行車安全性指標幅值對比見表4。

表4 列車行車安全性指標幅值對比
由表3可知:①不考慮地震動水力會使計算得到的橋梁橫向位移、橋梁橫向加速度和鋼軌橫向位移偏小。對于本文的計算條件,主梁跨中斷面的橫向位移、橫向加速度和鋼軌橫向位移的平均值分別偏小6.4%、30.0%和17.7%。②兩種模型的豎向動力響應幅值的相對誤差均小于1%。分析原因可知,考慮地震動水力后,斜拉橋下部結構與水接觸部分的縱橫向質量增加了,而其豎向質量無變化,這會改變斜拉橋的縱橫向自振特性,而對其豎向振型幾乎無影響。
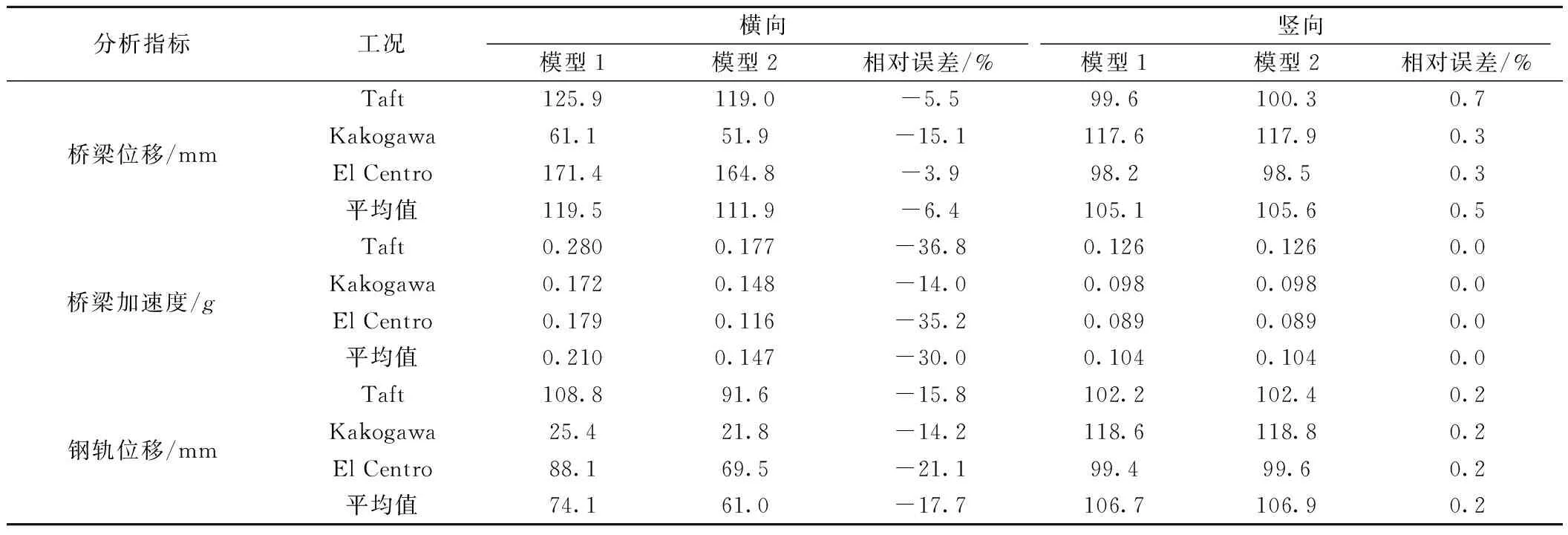
表3 主梁跨中斷面動力響應幅值對比
由表4可知:①不同地震波作用下,不考慮地震動水力會使計算得到的脫軌系數幅值、輪重減載率幅值和輪對橫向力幅值偏小。對于本文的計算條件,3條地震波作用下的平均值分別偏小4.5%、4.4%和6.0%。②不同地震波作用下,地震動水力對橋上列車的行車安全性指標的影響大小不同。例如,不考慮地震動水力時Taft、Kakogawa、El Centro地震波作用下的脫軌系數分別偏小7.8%、3.4%、1.8%。這是由于地震動水力改變了橋梁結構的縱橫向自振頻率,而不同地震波包含的頻率成分不同,因此其影響大小也不一樣。由此可見,在研究地震作用下高速鐵路跨海斜拉橋的行車安全性時需輸入多條地震波進行綜合評判。
綜上所述,對于高速鐵路跨海斜拉橋,不考慮地震動水力會低估橋梁、橋上軌道的橫向動力響應以及列車的行車安全性指標,可能造成對橋上列車行車安全的誤判。
3.3 行車安全性討論
根據前述分析,對于高速鐵路跨海斜拉橋,地震動水力的影響不可忽略。本節考慮地震動水力的影響,以模型1為分析對象,考察不同水平地震發生時過橋車輛的行車安全性。分析中,列車過橋的車速取275~375 km/h、間距為25 km/h,地震動峰值加速度分別取0.05g、0.10g、0.15g以及無震4個水平。根據TB 10002—2017《鐵路橋涵設計規范》[22],采用指標1~指標3來評判列車過橋時的行車安全性,其限值為
(11)
式中:Q為輪軌橫向力;P為輪軌垂向力;ΔP為輪重減載量;P0為車輪靜輪重。根據車輛參數,Q的限值為57.69 kN。不同強度地震作用下脫軌系數、輪重減載率和輪對橫向力幅值隨車速的變化曲線見圖9,圖9中幅值為3條地震波計算的絕對最大值。

圖9 列車行車安全性指標隨車速的變化曲線
由圖9可知,列車的脫軌系數、輪重減載率和輪對橫向力幅值均隨地震動峰值加速度的增大而增大,且列車過橋的車速越快,其幅值也越大。由此可見,對于高速鐵路跨海斜拉橋,地震動峰值加速度和車速是影響橋上列車行車安全的兩個主要因素。根據各個指標的限值,可以得到高速列車過橋時的安全車速閾值,見表5。

表5 列車安全車速閾值
在表5中,采用不同指標得到的安全車速閾值有差異,因此可綜合3個指標來共同評判列車過橋時的行車安全性。其中,無震時的安全車速閾值為375 km/h,而0.05g、0.10g、0.15g三個水平地震作用下的安全車速閾值分別為325、300、275 km/h。由此可見,無震時高速列車以設計車速350 km/h通過該跨海斜拉橋是安全的,而多遇地震(0.05g)和設計地震(0.15g)下高速列車過橋時的安全車速分別降低到設計車速的92.9%和78.6%。
4 結論
本文在已有程序Ttbsas的基礎上,采用剛性柱法計算地震動水力,研究了地震作用下高速鐵路跨海斜拉橋的行車安全問題。得到了以下幾點結論:
(1)地震動水力對高速鐵路跨海斜拉橋及橋上鋼軌的橫向動力響應影響顯著,而對其豎向動力響應幾乎無影響。對于本文的計算條件,不考慮地震動水力會使主梁跨中斷面的橫向位移、橫向加速度和鋼軌橫向位移分別偏小6.4%、30.0%、17.7%。
(2)對于高速鐵路跨海斜拉橋,不考慮地震動水力會使橋上的列車行車安全性指標偏小,可能造成對橋上列車行車安全的誤判。對于本文的計算條件,列車的脫軌系數、輪重減載率和輪對橫向力會分別偏小4.5%、4.4%、6.0%。
(3)對于高速鐵路跨海斜拉橋,橋上列車的安全車速閾值隨地震動強度的增加而降低。對于本文的計算條件,無震時的安全車速閾值為375 km/h,而0.05g、0.10g、0.15g三個水平地震作用下的安全車速閾值分別為325、300、275 km/h。
本文針對高速鐵路跨海斜拉橋分析了地震動水力的影響,但研究中忽略了水面波浪的作用。這對于大部分浪高小、波浪作用不突出的海灣橋梁是適用的,但對于一些波浪作用不能忽略的高速鐵路跨海橋梁,還需研究地震-波浪聯合作用下的車橋耦合振動問題。

