基于增量磁導率的鋼軌頻變阻抗曲線計算

武偉康，陳劍云，劉思然，傅欽翠

(1.中鐵第六勘察設計院集團有限公司 電氣化設計院分公司，天津 300250； 2.華東交通大學 省部共建軌道交通基礎設施性能監測與保障國家重點實驗室，江西 南昌 330013)

鋼軌作為牽引供電系統的主要回流導線，其阻抗特性是牽引供電計算和暫態信號分析的重要參數。由于鋼軌是鐵磁材料，具有非線性的磁滯特性，致使其內阻抗隨頻率變化更為明顯。鋼軌內阻抗特性，一般都是基于鋼軌基本磁滯曲線的磁導率計算得到。然而，在針對牽引供電系統暫態行波傳播特性的研究過程中，暫態行波一般是疊加在大電流基波上的一組高頻信號，這些高頻暫態信號在鋼軌上傳播的阻抗特性不同于低頻大電流信號。對于低頻大電流信號而言，鋼軌磁化會不斷遍歷一個個完整的回形磁滯曲線過程，而對于短暫的高頻信號，其變化周期短，幅度相對較小，往往是在基本磁滯曲線的某個點上形成一個小的環形磁化過程曲線，因此，有必要針對高頻小信號研究其增量磁導率，并以此為基礎，計算出高頻小信號的鋼軌頻變內阻抗特性曲線。

針對一般的牽引供電計算，文獻[1-2]對鋼軌的內阻抗計算進行了研究，如大電流下鋼軌的磁化特性，使用磁導率曲線計算鋼軌內阻抗等；并采用有限元方法進行計算，取得了較好的計算結果[3-5]。然而，針對暫態情況下鋼軌的內阻抗計算，現有文獻資料的研究計算尚不充分。高頻暫態信號通常是疊加在穩態大電流基礎之上的，即構成了大電流偏置磁場下的小信號增量磁場的情形[6-8]。鐵磁材料在暫態信號作用下，會形成局部磁滯回線，且通常定義增量磁導率用來表征鐵磁材料的局部磁滯曲線特性[9-11]。此外，有限元方法不僅可以高精度地計算鋼軌工字型截面形狀，而且可以計算其鐵磁特性[12]。多數文獻均采用有限元方法[3-5,13-14]計算鋼軌的頻變阻抗參數。

本文針對目前電氣化鐵路廣泛使用的P60型鋼軌展開研究與計算，主要分析研究大電流疊加高頻小電流信號作用下鋼軌的磁化機理和過程，根據P60鋼軌B-H基本磁化曲線，導出鋼軌的增量磁導率曲線，并將其添加到Ansys Maxwell計算模型中，計算出暫態情況下P60鋼軌寬頻率范圍(0～10 MHz)的頻變阻抗特性曲線。

1 穩態大電流信號下鋼軌磁化特性

1.1 鋼軌的基本磁化特性

鋼軌是典型的鐵磁材料，磁導率的非線性變化加劇了電流趨膚效應的程度，使鋼軌的內阻抗隨電流的變化而更加明顯，考慮鋼軌的磁化特性是精確計算其內阻抗的前提。在牽引供電計算中，鋼軌作為牽引回流的重要導線，可認為鋼軌中通以穩態大電流，即處于大電流信號形成的磁場環境中。

在穩態大電流的磁化作用下，其過程具有較強的非線性、時滯性等[9]特點。磁感應強度B(或磁化強度M)對于磁場強度H的關系通常表現為回線的形式，分別被稱為磁滯回線和磁滯回線族，如圖1所示[15]。

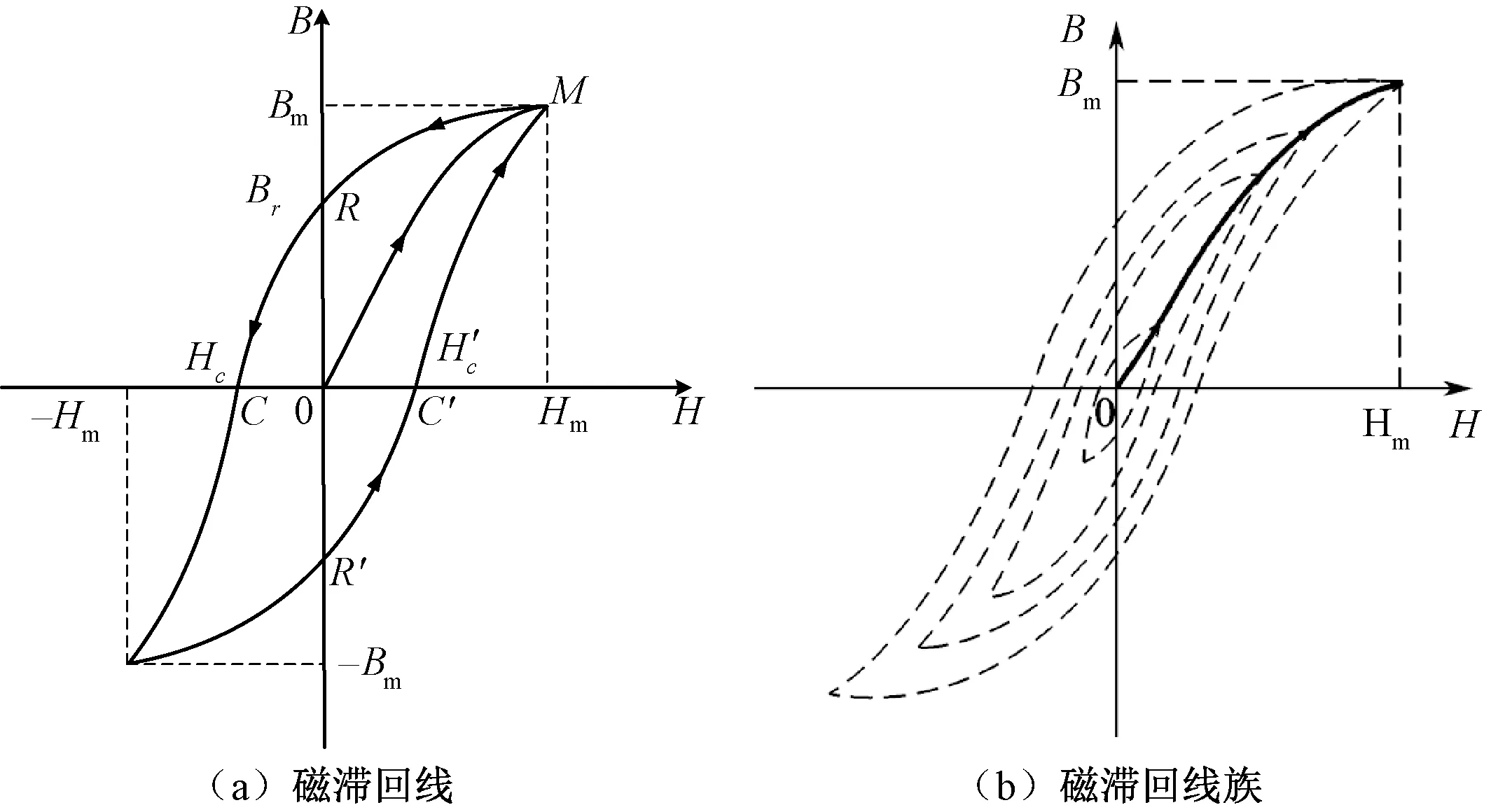
圖1 鐵磁材料的磁滯回線(族)

磁化曲線是鐵磁材料的固有屬性，通常由實驗方法測定，本文對P60鋼軌的鐵磁特性進行了檢測，獲得P60鋼軌B-H磁滯回線和基本磁化曲線，如圖2所示。P60鋼軌其他磁特性參數見表1。

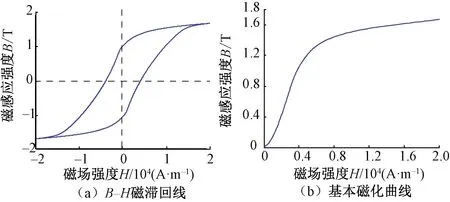
圖2 P60鋼軌的磁化特性曲線

表1 P60鋼軌其他磁特性參數

1.2 鋼軌的基本磁導率曲線

磁導率可以定量描述磁性材料的磁化特性，磁場中各物理量之間的關系如下[16]：

對于線性且各向同性材料，通常B、H和M的關系可以表示為

B=μ0(H+M)

( 1 )

若定義材料的磁化率為χm，則有

M=χmH

( 2 )

B=μ0(H+χmH)=μ0μrH

( 3 )

磁導率μ的定義為

μ=μ0μr

( 4 )

為了使用方便，通常使用μr進行計算，即

( 5 )

式中：μ為材料的磁導率；μ0為真空磁導率；μr為相對磁導率。

根據式( 5 )及圖2(b)，可以得出P60鋼軌的基本磁導率曲線，如圖3所示 。值得注意的是，鋼軌的磁導率呈非線性變化，計算其內阻抗時不能視其為定值。

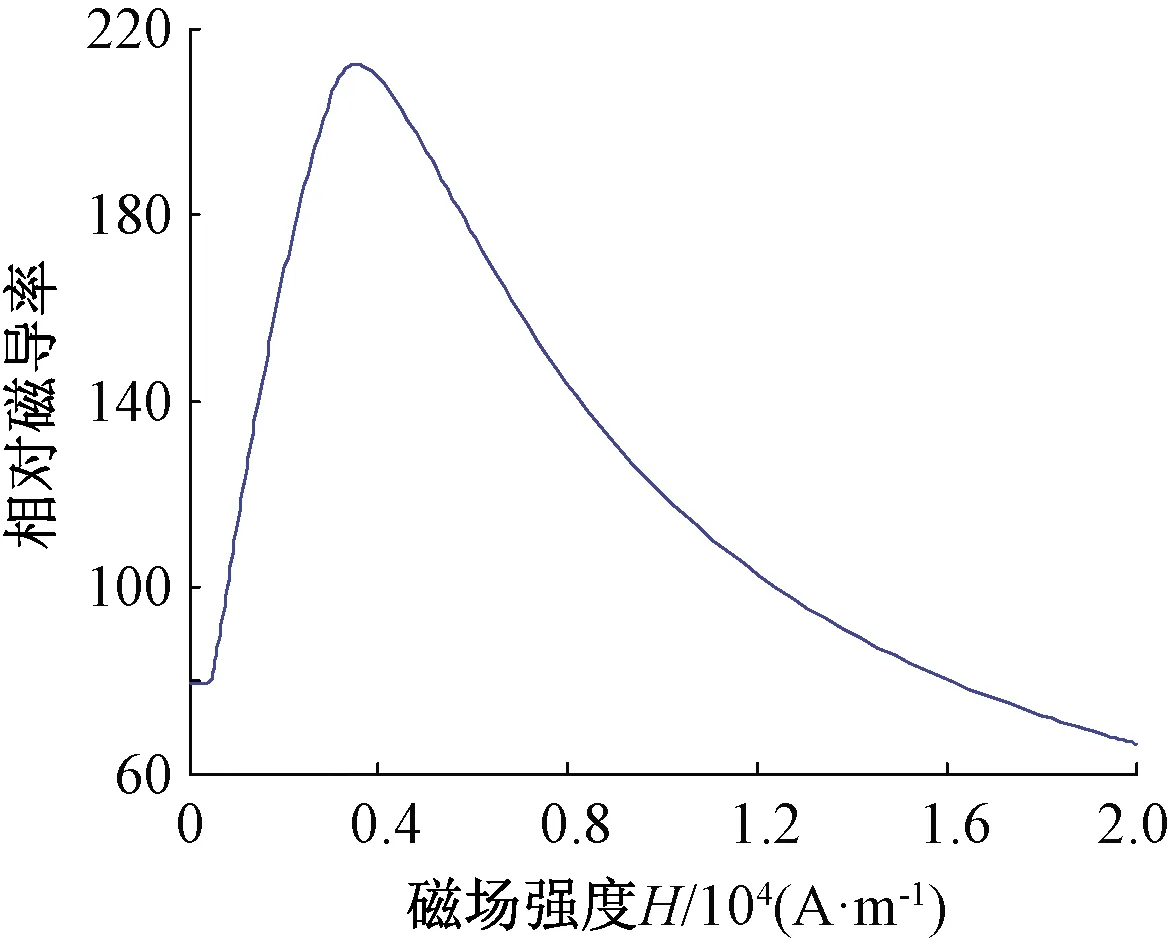
圖3 P60鋼軌基本磁導率曲線

2 暫態小電流信號下鋼軌磁化特性

2.1 鋼軌的局部磁滯回線

在實際的牽引供電系統中，鐵路線路諧波擾動等瞬態情況時常發生，除了穩態大電流的磁場外，還會疊加一些暫態小電流信號，如圖4所示。特別是當牽引網發生短路故障時，產生行波等暫態信號，這些信號可能在鋼軌的基本磁滯回線內形成局部磁滯回線。

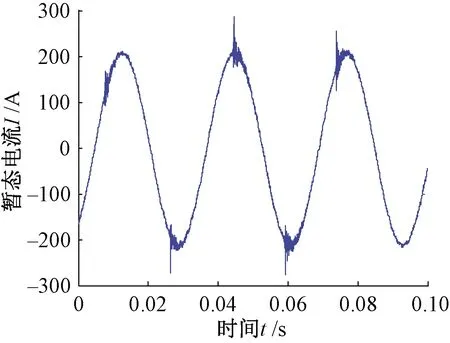
圖4 暫態信號擾動下電流波形

如圖5(a)所示，假設在回線上的任一點a處，小范圍ΔH內往返變化一次或多次，可以生成一條小回線[15](亦稱局部回線)。若存在多個不同的偏置磁通密度，則可能會形成多個局部回線，如圖5(b)所示。

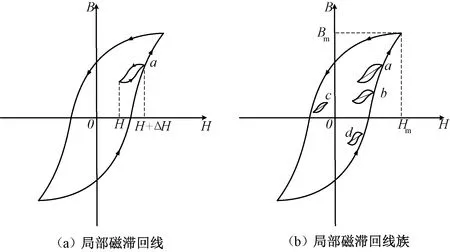
圖5 鐵磁材料的局部磁滯回線(族)

2.2 鋼軌的增量磁導率曲線

如果在一定的偏置磁場強度H下，疊加的小信號磁場的磁化軌跡將以恒定磁場H的工作點為中心形成一小增量環[10]，如圖6(a)所示。由于增量環變化周期短，幅值相對較小，可將其近似地做線性處理，取此增量環兩頂點間連線的斜率，即為材料的增量磁導率μinc。

( 6 )

式中：ΔB、ΔH分別為磁感應強度和磁場強度幅值的增量。增量磁導率是定義在基本磁化曲線基礎上的一種動態磁導率[9]，μinc值也是一條非線性曲線。根據式( 6 )及圖2(b)，可以得出P60鋼軌增量磁導率曲線，如圖6(b)所示。

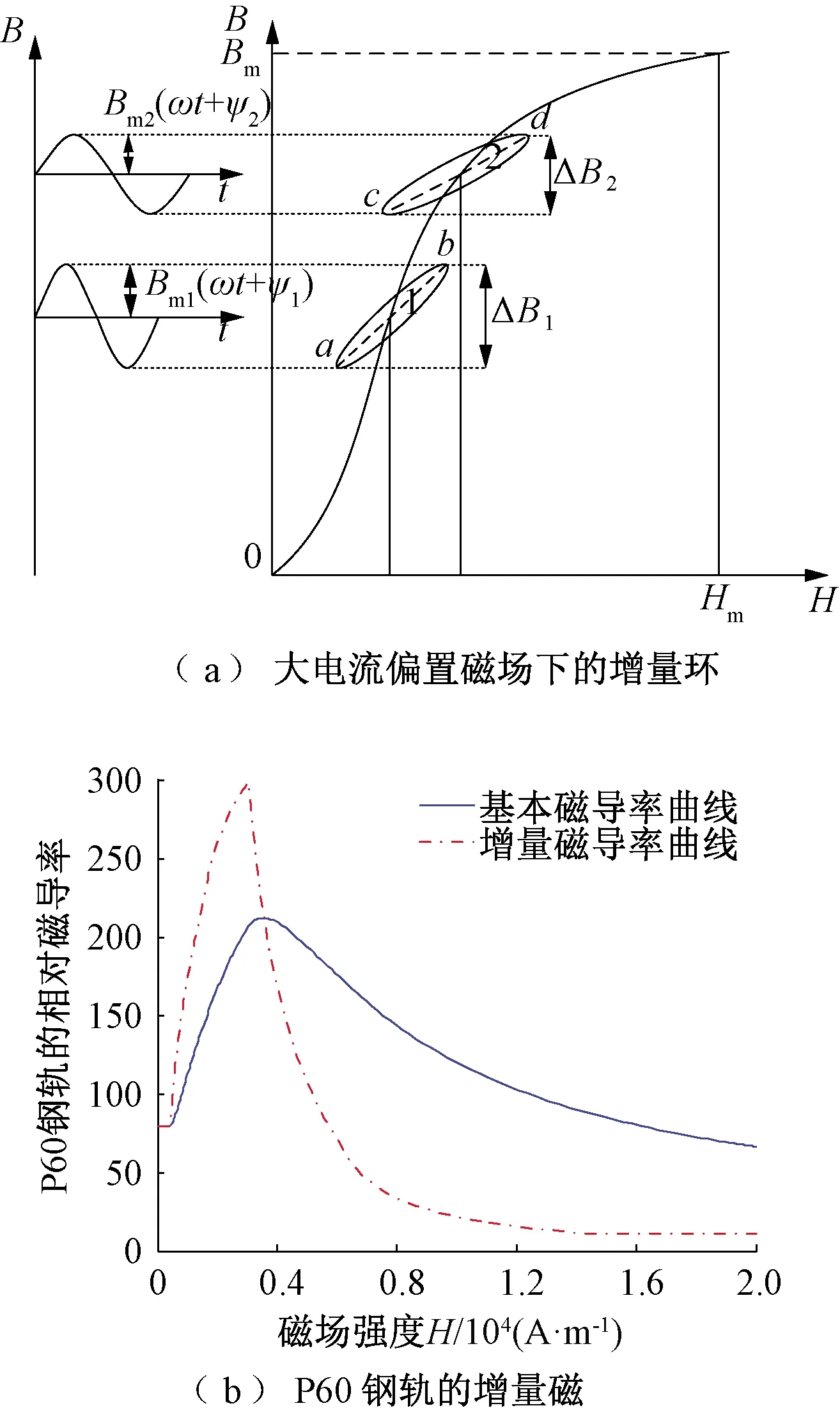
圖6 P60鋼軌增量磁場下的磁化曲線

3 鋼軌內阻抗有限元軟件計算

3.1 計算模型邊界條件設定

在Ansys Maxwell軟件中，導入P60鋼軌的Auto CAD圖形，建立計算模型，如圖7所示。

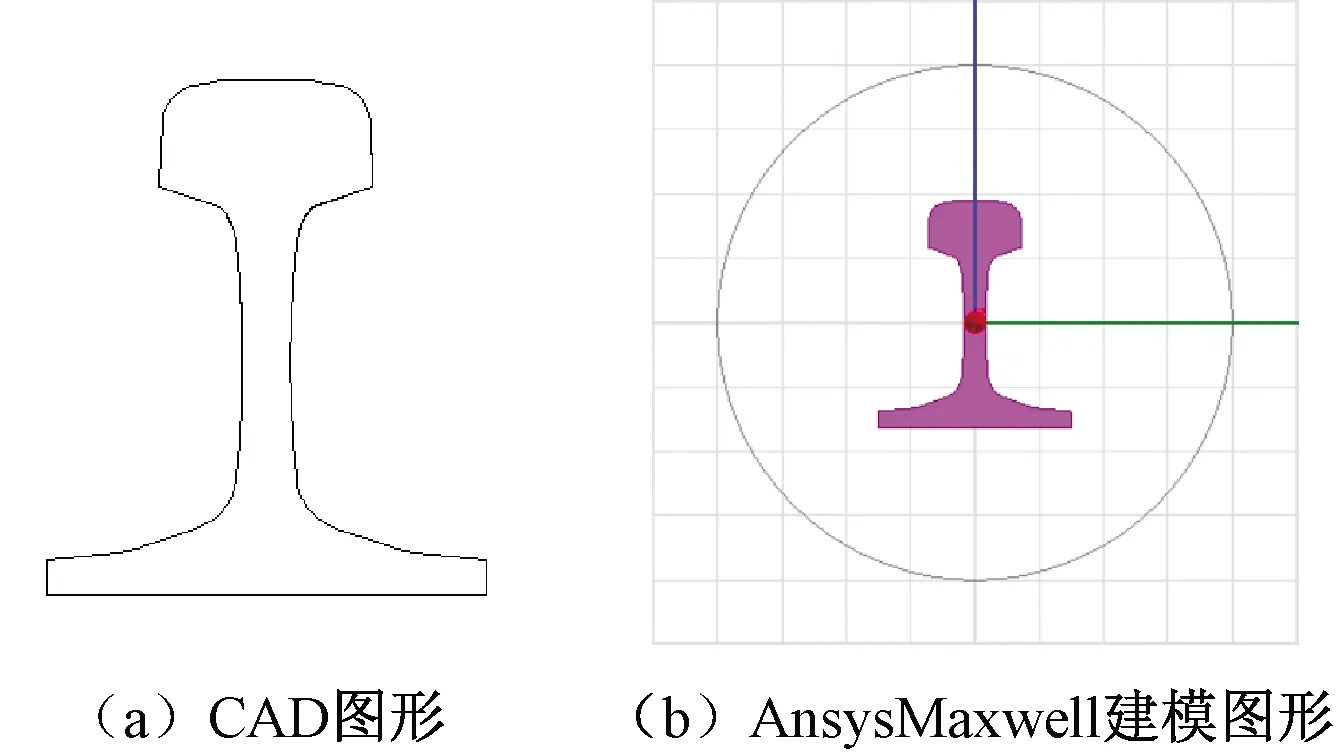
圖7 P60鋼軌計算模型

設置計算模型參數時，應首先設置場求解器為渦流場，這樣可有效添加P60鋼軌B-H曲線及其他基本材料屬性，見表2。其次，如圖7(b)所示，模型中P60鋼軌外圍設置的圓，外圓半徑的大小，只影響模型外電感值，而不影響鋼軌的內電感值，仿真計算時也驗證了這一點，本文中外圓半徑設為R=200 mm。在圓的邊界上，設置狄利克雷邊界條件；在鋼軌上設置電流源激勵。在求解過程中，計算鋼軌內阻抗的起始頻率為0.1 Hz，最高頻率為10 MHz，共計127個頻率點。

表2 P60鋼軌基本材料屬性

3.2 P60鋼軌計算結果圖

計算完成后，可根據需要在計算區域繪制不同類型的場圖，P60鋼軌的仿真計算結果如圖8所示。

如圖8(a)所示，對鋼軌的網格劃分，表層的密集程度大于內部，比較直觀地反映出交流電流的集膚效應；圖8(b)中鋼軌的磁場強度由外向內逐步減弱，中心最弱。圖8(c)、圖8(d)直觀呈現了鋼軌內、外部的磁力線分布情況。

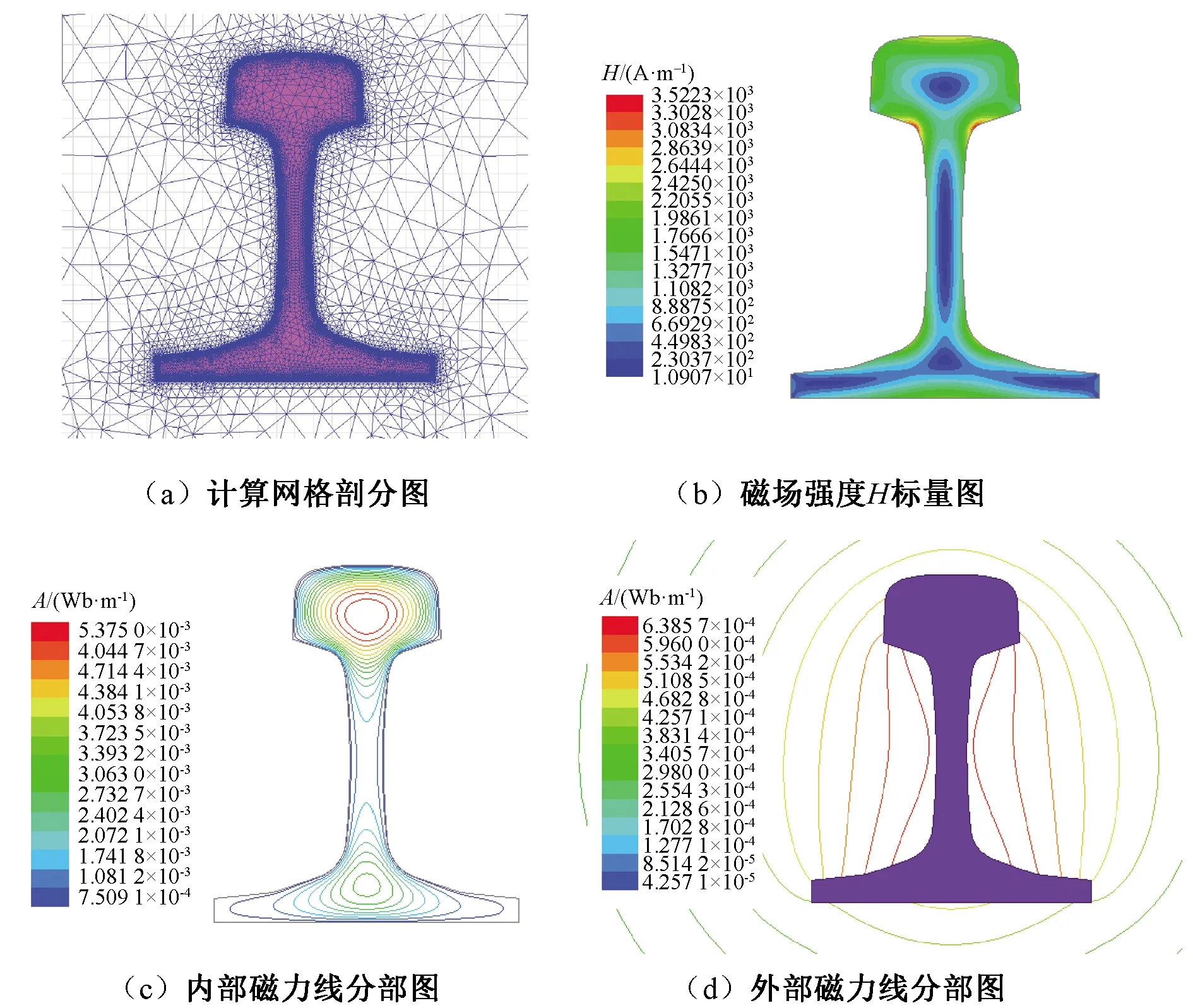
圖8 P60鋼軌的有限元計算結果

4 鋼軌內阻抗頻變曲線分析

4.1 直流內阻抗

導體內阻抗包含內電阻和內電感兩部分，當電源頻率為零時，即為導體的直流內阻抗。可根據式( 7 )、式( 8 )對鋼軌直流內阻抗進行計算[17]。

( 7 )

( 8 )

直流電阻Rd與導體的電阻率ρ及橫截面面積有關，而直流電感Ld只與導體材料的磁導率有關。由圖5(b)可知，P60鋼軌的起始相對磁導率μr=79.58，則P60鋼軌的直流電阻和直流電感為

2.1467×10-5Ω/m

3.979×10-3H/km

4.2 暫態情況下鋼軌的頻變阻抗曲線

通過對計算結果進行分析，電流源激勵的幅值是影響鋼軌內阻抗計算的主要因素，如圖9所示。

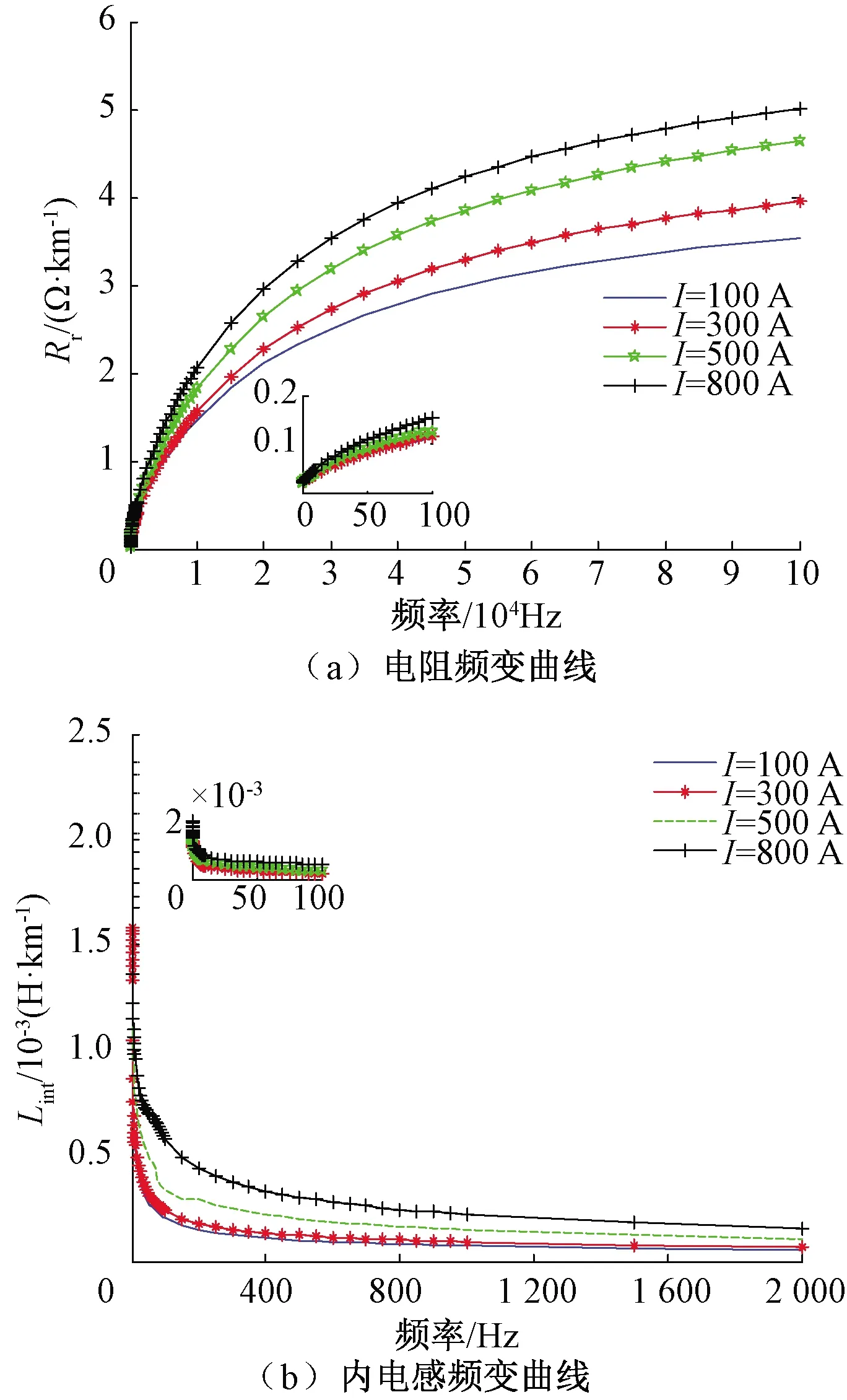
圖9 不同幅值電流下P60鋼軌阻抗頻變曲線

為更清晰地呈現交流電阻Rr和內電感Lint的頻變特性，繪圖時分別將頻率范圍設置為0～100 Hz和0～2 000 Hz，以下同理。表3、表4分別給出不同幅值電流源下鋼軌的交流內阻及內電感計算結果。

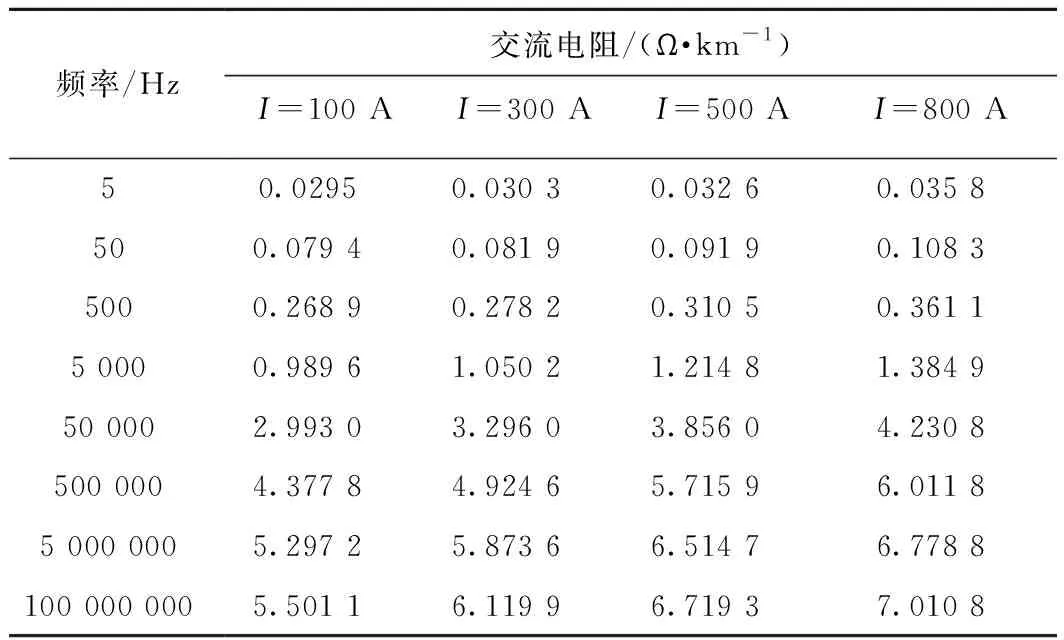
表3 不同幅值電流源下P60鋼軌交流電阻值

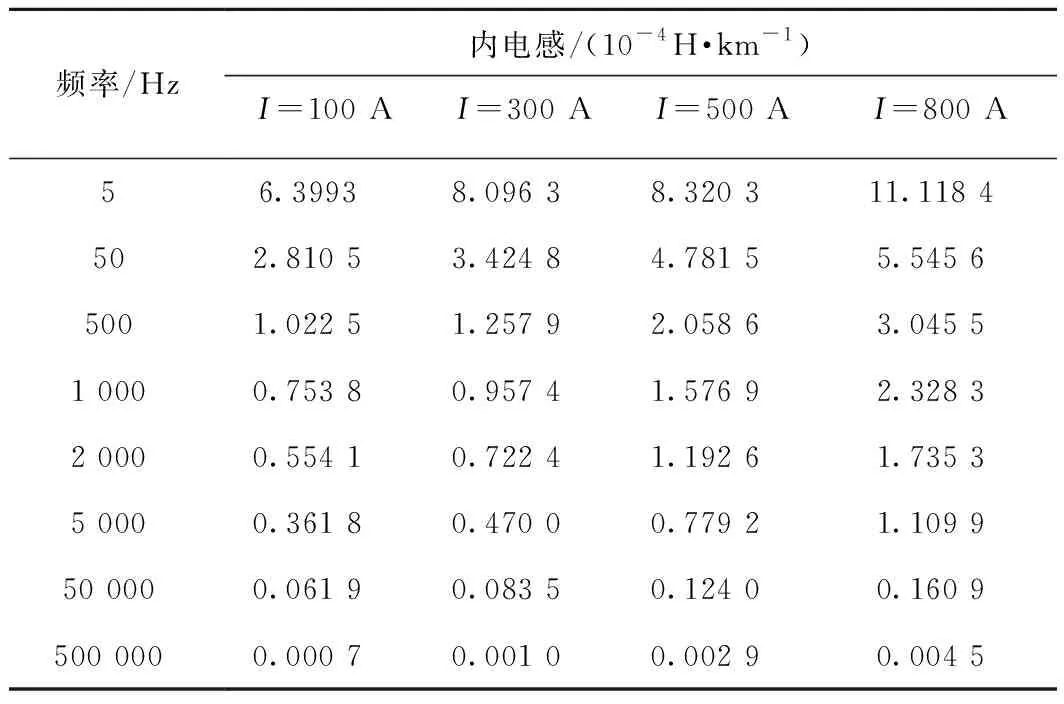
表4 不同幅值電流源下P60鋼軌交流內電感的部分結果

4.3 暫態信號擾動與大電流信號頻變阻抗曲線對比

通過對比計算高頻暫態信號和低頻大電流信號下鋼軌阻抗頻變曲線，可以反應出兩者的不同，如圖10所示。表5、表6對應圖中曲線給出部分計算結果。

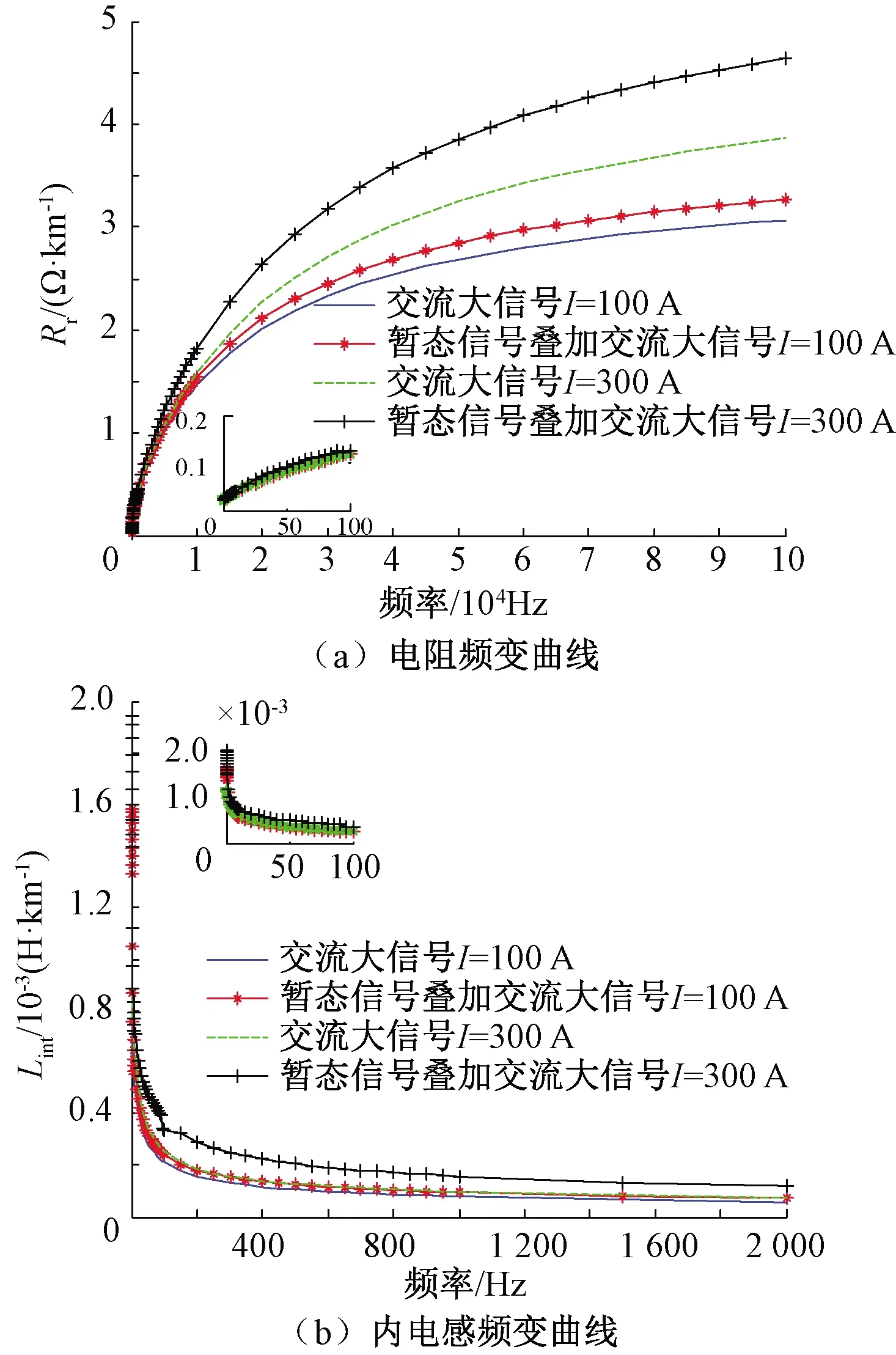
圖10 P60鋼軌，暫態和穩態下的頻變阻抗曲線對比

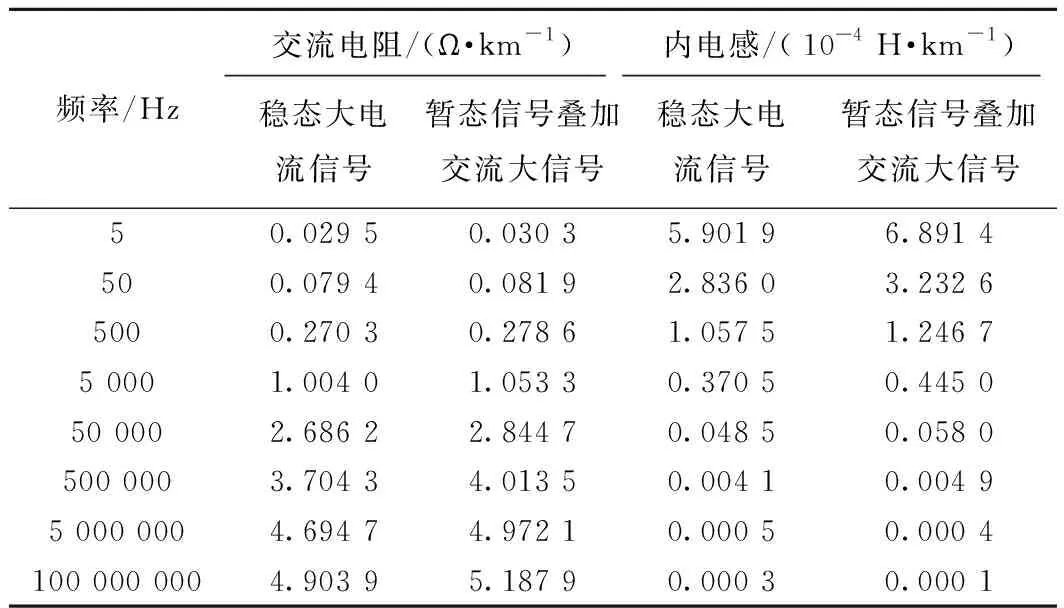
表5 暫態及穩態下P60鋼軌交流內阻抗的部分結果(I=100A)

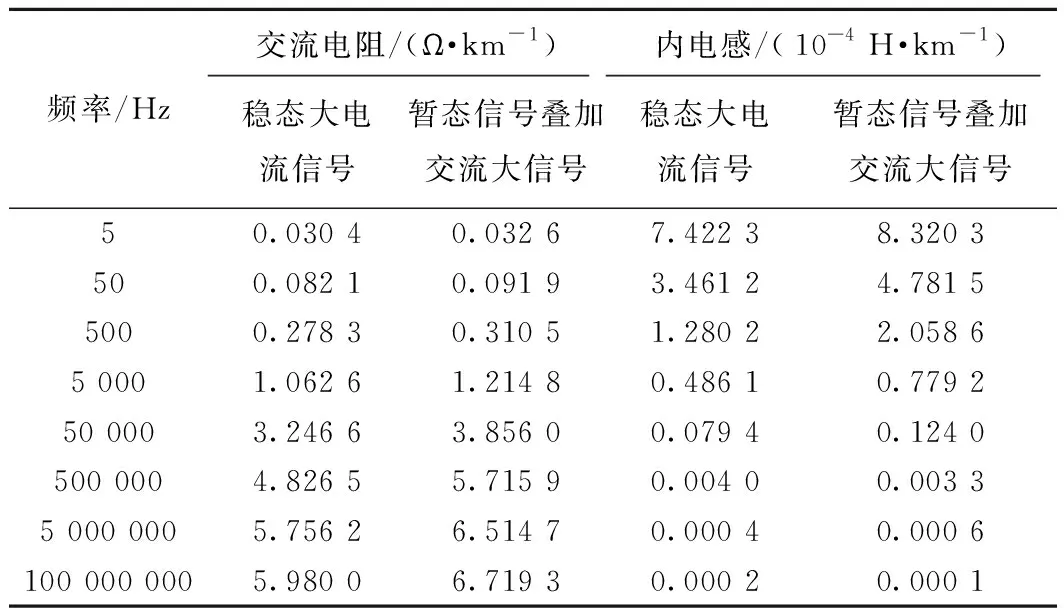
表6 暫態及穩態下P60鋼軌交流內阻抗的部分結果(I=300A)

5 結論

通過使用有限元軟件Ansys Maxwell，對暫態信號下P60鋼軌的磁化機理和特性進行分析計算，并給出0～10 MHz頻率范圍內鋼軌的頻變阻抗曲線和具體數值，這些曲線和參數為牽引供電系統進行時頻電磁暫態分析提供基本參數。分析計算結果，可以得出以下結論：

(1)鋼軌中的電流不斷增大時，其交流電阻和內電感值均有所增加；在同一電流下，交流電阻隨頻率的升高而增大，內電感隨頻率的升高而減小，且當頻率趨于300 kHz時，可近似認內電感減小到零。

(2)高頻暫態信號在鋼軌上傳播的阻抗特性與低頻大電流信號不同。高頻暫態信號疊加大電流信號形成的增量磁場，使鋼軌的交流電阻和內電感值在同一條件下均有所增加，且交流電阻值的差異主要在10 kHz頻率以上，內電感值的差異主要在0～5 000 Hz頻率段。