基于改進ELM的鋰離子電池RUL預測

唐 婷,袁慧梅

(首都師范大學信息工程學院,北京 100048)

鋰離子電池在使用一段時間后會出現老化,影響使用性能,因此,需要準確預測剩余使用壽命(RUL)。RUL的預測方法可以分為3類:模型法、數據驅動法和混合方法[1]。

數據驅動中的神經網絡在RUL估計方面具有很大的潛力。神經網絡雖然非線性映射能力好,但參數眾多、結構復雜,在網絡訓練過程中會耗費大量時間,占用很多內存,因此,研究者期望尋找一種既能節省成本,又能準確預測RUL的方法。極限學習機(ELM)是一種特殊的單隱含層前饋神經網絡,結構簡單,無需反向傳播技術更新參數值,學習速度快,泛化能力強。姜媛媛等[2]提取等壓降放電時間作為電池間接壽命特征參數,用ELM構建參數與電池容量的關系模型,間接預測RUL。該算法操作簡單,只需構建訓練集和測試集,就能很好地預測電池的容量,但參數為隨機產生,預測結果不穩定,魯棒性較差。吳婧睿[3]引入螢火蟲算法,優化ELM隨機生成的輸入權值和隱藏層偏置值,減小了預測誤差。該算法雖然提升了魯棒性,但對優秀個體的依賴程度很高,要求感知范圍內有優秀個體提供信息,否則將停止搜索,降低了收斂速度,甚至可能找不到最優個體。R.Razavi-Far等[4]用ELM進行一步和多步提前預測,作為預測模塊,使用多種預測策略,利用恒流實驗的容量數據估計RUL。該算法雖然在RUL的短期和長期范圍預測較精確,但參數隨機產生,仍存在不穩定性。Y.Y.Ma等[5]開發廣義學習的ELM,并不斷地擴展輸入層、增加輸入層的節點,提高了網絡捕獲數據中有效特征信息的能力。該算法雖然預測精度較高,但輸入層的不斷擴展使得網絡結構越來越復雜,計算量增大。

傳統的ELM預測鋰離子電池的RUL時,會出現結果發散及精度不高等問題,減弱了算法的魯棒性和泛化能力。對ELM的改進,目前有按一定規則增加或減少隱藏層節點數量、優化參數算法及引入核函數等方法。G.B.Huang等[6]結合ELM算法和核函數,用核函數映射代替ELM中的隨機特征映射,形成了核極限學習機(KELM);N.Y.Liang等[7]提出在線順序極限學習機(OS-ELM),通過新數據的引入,不斷更新網絡參數,實現在線訓練;楊新星等[8]通過不同的優化算法,對ELM中的參數進行尋優,提升預測精度。以上研究均采用全連接或核函數,改進ELM算法輸入層與隱藏層之間的映射關系,而局部連接的ELM結構并未得到廣泛的關注。這些改進都增加了計算量,很多參數需要初始化,若選擇不當,會對預測結果造成影響。此外,A.M.Saxe等[9]提出的具有隨機權重的單層卷積平方池體系結構及G.B.Huang等[10]提出的基于局部感受野的ELM,都說明構造一個特定的網絡結構能大幅提高系統性能,效果好于一些深度學習算法,并可提高訓練速度。M.Lin等[11]提出用全局平均池化的方法代替全連接層,即把最后一個多層感知器卷積層所得到的每一張特征圖進行全局平均池化。每張特征圖都可得到一個輸出,能節省參數,降低網絡的復雜度,避免過擬合。

綜上所述,本文作者引入卷積神經網絡和全局平均池化,對ELM進行兩種改進,并對算法的效果進行驗證。

1 改進的ELM

ELM的改進算法很少關注局部連接的ELM結構,因此,本文作者提出兩種改進算法。改進算法A把ELM輸入層與隱含層之間的全連接關系改為卷積運算操作,即引入一個常規大小的卷積核,視為原隱含層權重的變形,與輸入層的數據進行卷積,提取特征矩陣,經平均池化后,得到隱含層輸出矩陣H,后續獲取輸出權重矩陣β的方式與標準ELM一致。由于改進算法A中的卷積核和偏置的取值都是隨機產生的,運行結果有不確定性。

為提高算法的魯棒性,受全局平均池化思想的啟發,改進算法B直接把ELM輸入層與隱含層之間的全連接關系改為池化,即輸入層的數據直接經池化操作得到隱含層輸出矩陣H,而輸出權重矩陣β的獲取也與標準ELM一樣。值得注意的是,由于輸入層的數據只是一個矩陣,即相當于一個特征圖,需要采用傳統的平均池化方法對矩陣進行降維,而非直接進行全局平均池化。

1.1 改進算法A

①數據預處理。從循環周期開始,以每連續10個循環周期的數據作為一組輸入,下一個循環周期的數據用作輸出,分別對兩組電池數據進行構建,之后選定預測起始點T,可得到訓練集的輸入矩陣Ptrain、輸出矩陣Ttrain和測試集的輸入矩陣Ptest、輸出矩陣Ttest。

②初始化參數。初始化卷積核W、偏置B。

③對Ptrain進行卷積操作,得到訓練集的特征矩陣TH。

式(1)中:BM為B的復制擴展矩陣;*表示卷積運算。

④計算訓練集的非線性特征輸出矩陣NH與隱藏層輸出矩陣H。

式(2)中:g(x)為激活函數;mean_pooling代表平均池化。

⑤計算輸出權重矩陣β。

式(4)中:H+是H的廣義逆矩陣。

⑧得到最終的預測結果Y。

1.2 改進算法B

①數據預處理。與改進算法A的步驟①一致。

②計算訓練集的H。H由Ptrain進行平均池化得到。

③計算輸出權重矩陣β。計算公式見式(4)。

⑤得到最終的預測結果Y。計算公式見式(7)。

2 實驗及分析

2.1 數據集

實驗所用電池退化數據有兩組(見圖1)。第一組來自馬里蘭大學高級生命周期工程研究中心(CALCE)提供的鋰離子電池壽命數據[12];第二組采用美國國家航空航天局(NASA)艾姆斯預測卓越中心提供的鋰離子電池數據[13]。通常認為,鋰離子電池的放電容量下降到額定容量的60%～80%時,視為使用壽命終止(EOL)。將第一組電池額定容量的80%設置為EOL,第二組電池額定容量的71%設置為EOL,得到第一、二組電池的失效閾值分別為0.72 Ah、1.42Ah。

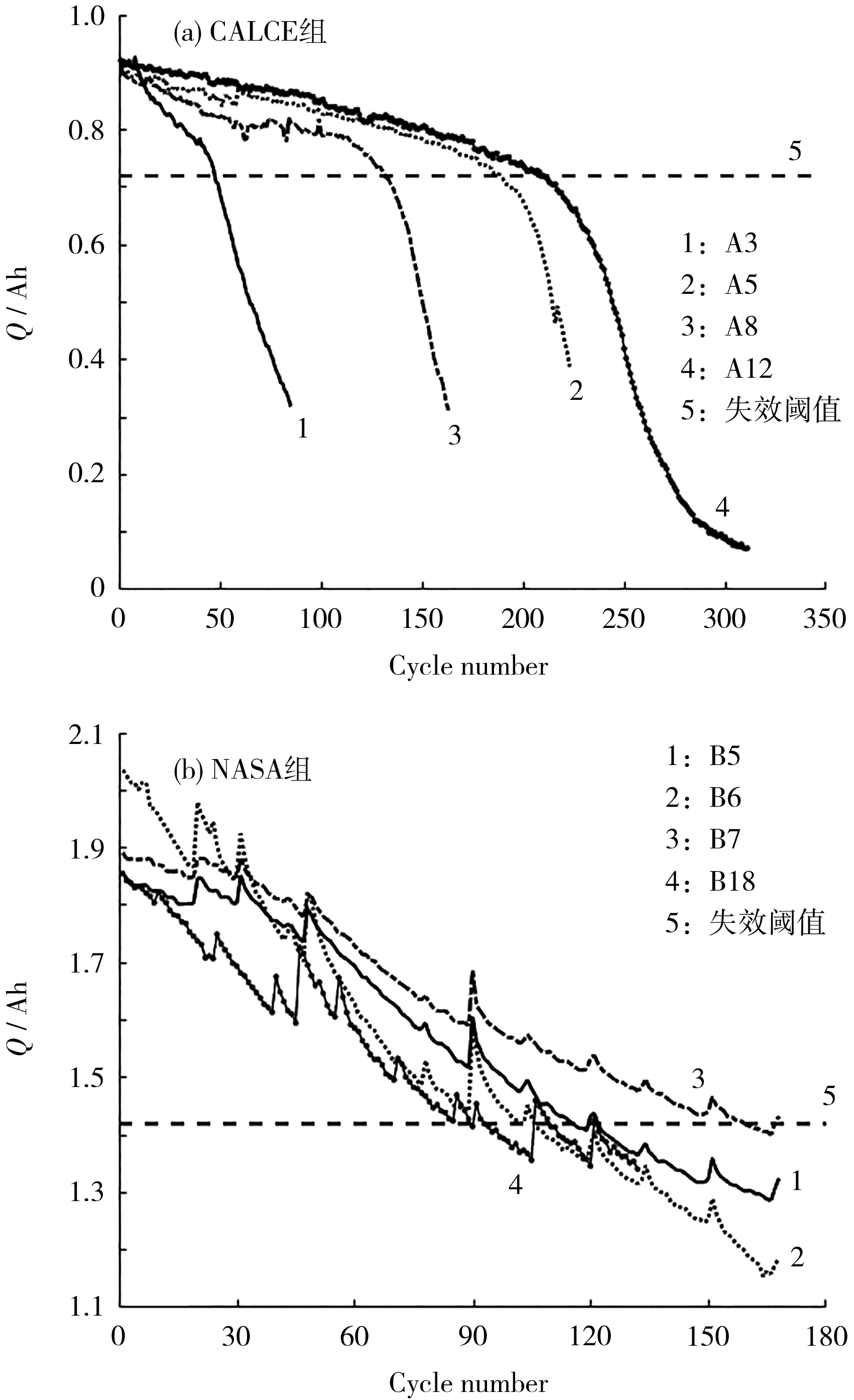
圖1 鋰離子電池的容量退化數據Fig.1 Capacity degradation data of Li-ion battery

2.2 參數設置

傳統的ELM的隱藏層節點數與訓練集樣本個數相等,輸入層與隱藏層之間的權重w和隱含層神經元的偏置b隨機均勻產生,激活函數采用正弦函數。改進算法A中,卷積部分設置為:卷積核大小為3×3,隨機均勻初始化卷積核和偏置的值,步長為1,方式為全零填充,激活函數同樣采用正弦函數。池化部分設置為:池化核大小為2×1,步長為1,方式為平均池化。改進算法B中池化部分的設置與算法A相同。采用2×1大小的池化核,以便計算得到后面的輸出權重矩陣β。由改進算法A的步驟⑤或改進算法B的步驟③可知:當劃分好訓練集與測試集,以及選定預測起始點之后,訓練數據的輸出矩陣Ttrain大小已被固定。為獲取β的值,需要經過池化操作,得到隱藏層輸出矩陣H匹配Ttrain的大小。

2.3 實驗結果

為客觀評價所提出算法的RUL預測性能,常用的評價指標有:均方根誤差(RMSE)、平均絕對百分比誤差(MAPE)、絕對誤差(AE)和相對誤差(RE)等。RMSE和MAPE反映預測容量值與真實容量值之間的偏差;AE和RE進一步反映RUL預測值(Rpre)偏離RUL真實值(Rtru)的程度。

2.3.1 與ELM變形算法的對比

為了驗證兩種改進ELM算法的良好預測性能,在相同的樣本數據下,與傳統的 ELM[2]、KELM[6]、OS-ELM[7]和粒子群優化極限學習機(PSO-ELM)[8]進行對比,具體各項評價指標見表1、2,預測結果如圖2所示。

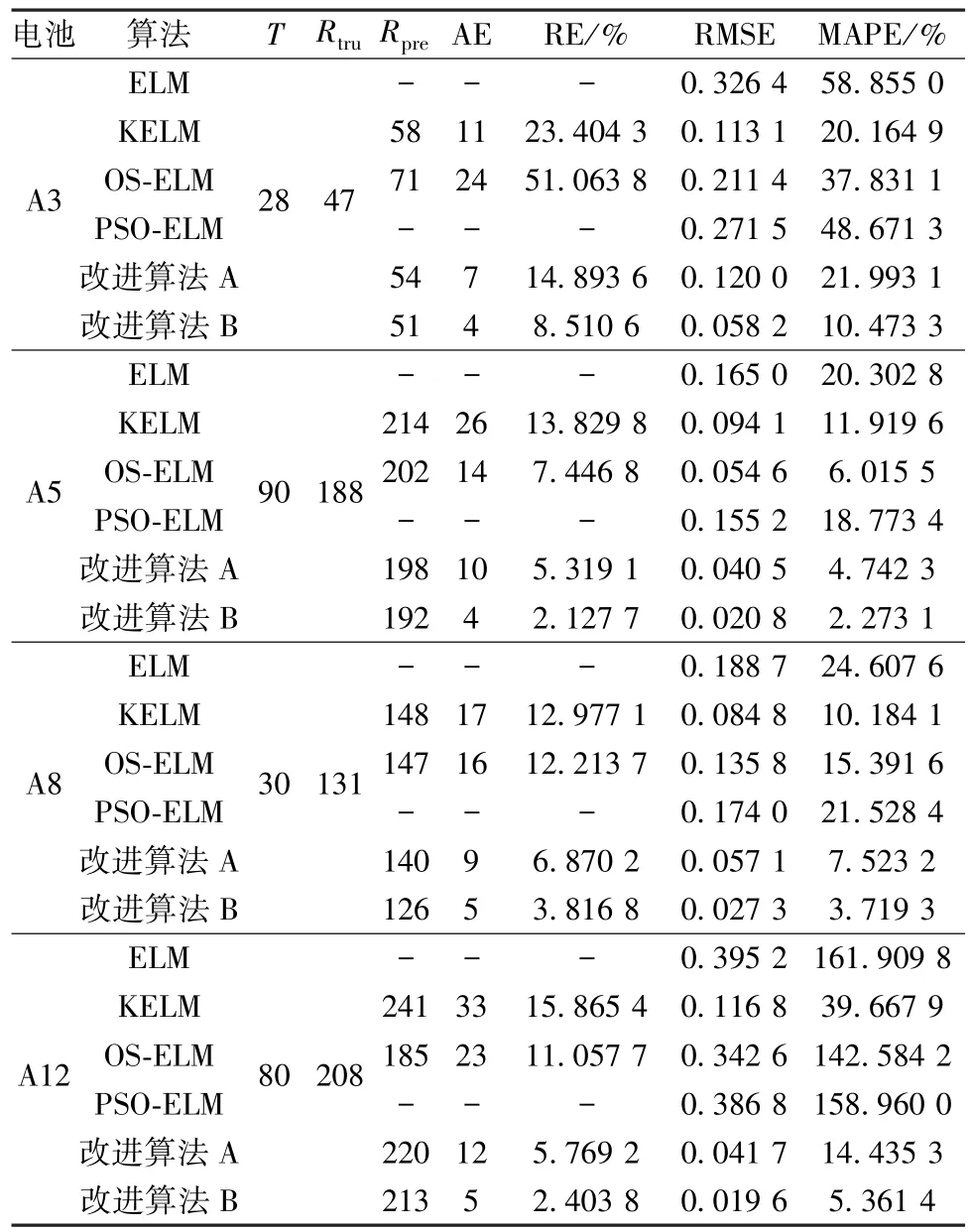
表1 CALCE組電池的預測結果比較Table 1 Comparison of prediction results for batteries of Center for Advanced Life Cycle Engineering(CALCE)

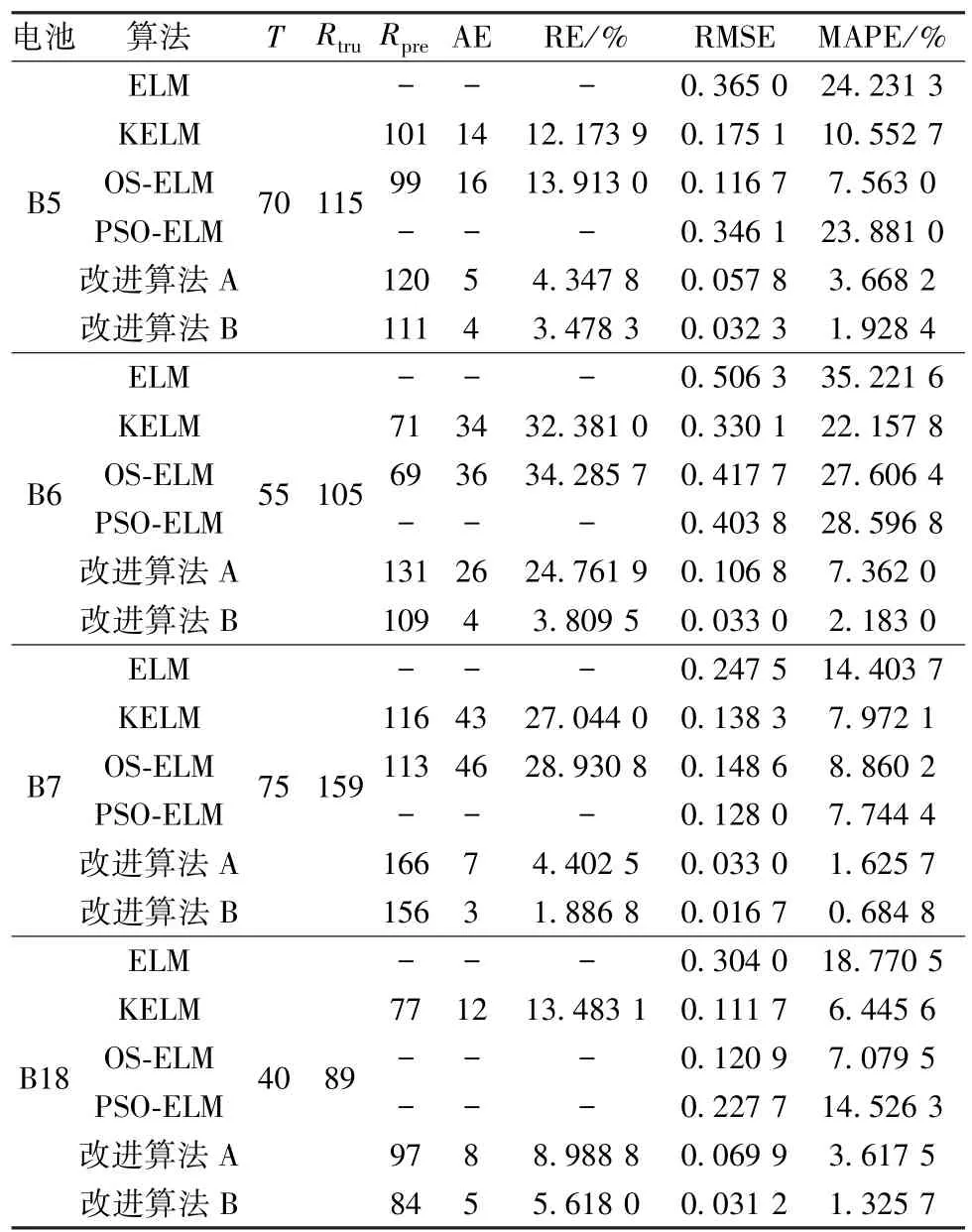
表2 NASA組電池的預測結果比較Table 2 Comparison of prediction results for batteries of National Aeronautics and Space Administration(NASA)

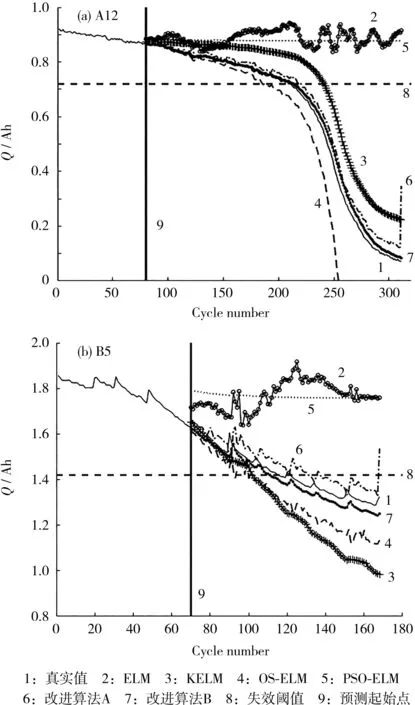
圖2 部分電池預測結果Fig.2 Prediction results of partial batteries

從實驗結果可知,傳統的4種算法對鋰離子電池數據的預測效果不理想,有的甚至達不到失效閾值點;而兩種改進的算法均比其他算法更加靠近真實值,表明兩種改進的算法對鋰離子電池的RUL預測是可行的。從各項評價指標值可見,當樣本為A3時,改進算法A預測容量的RMSE略微大于KELM,但所預測的RUL卻比KELM更接近于真實值,準確性更高。改進算法A改善了發散效果,在一定程度上降低了預測誤差;改進算法B去除了改進算法A預測結果的不確定性,提升了魯棒性,使結果更為可靠。

2.3.2 與神經網絡對比

為進一步驗證算法的泛化能力,以A12和B5電池為例,用目前較經典的神經網絡,即循環神經網絡(RNN)[14]、長短期記憶網絡(LSTM)[15]、門控循環單元(GRU)[16]和時間卷積網絡(TCN)[17]進行比較,結果列于表3。

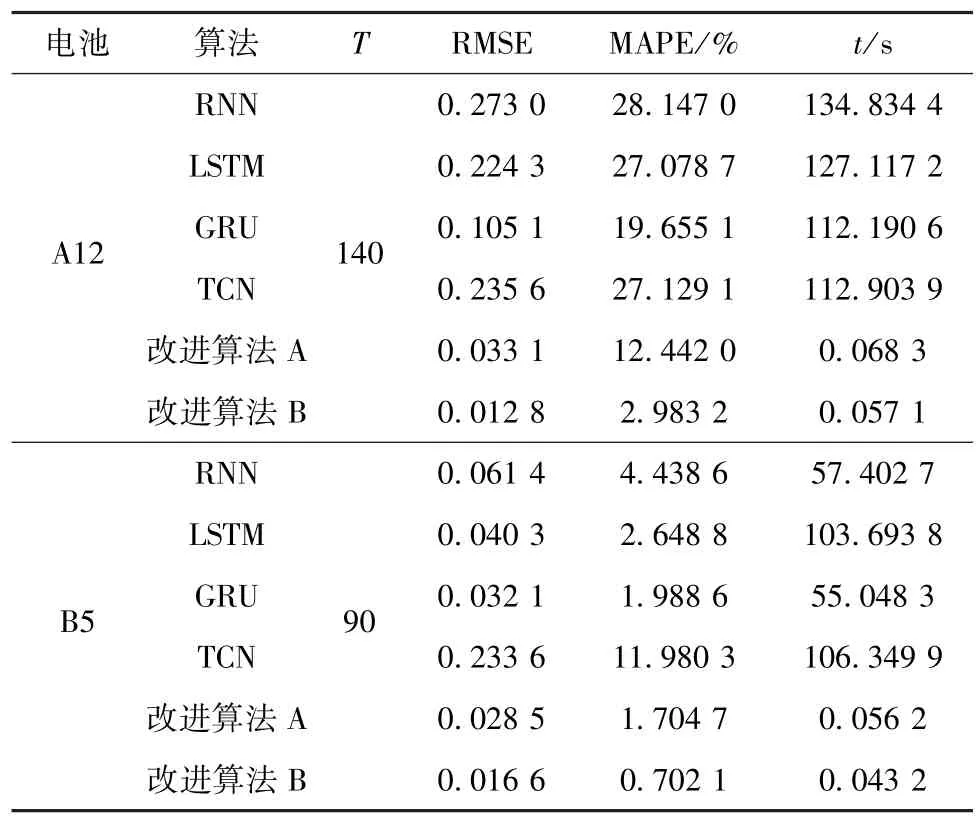
表3 A12和B5電池的預測結果比較Table 3 Comparison of prediction results for batteries of A12 and B5

從表3可知,與RNN、LSTM、GRU和TCN等經典的神經網絡相比,兩種改進的算法的預測準確度較高,且訓練、測試網絡所用時間較短,說明兩種改進的算法在預測精度和時間成本上都具有較大的優勢。

2.3.3 不同預測起始點對比

選取不同的預測起始點,用兩種改進的算法進行仿真實驗,預測結果如表4所示。

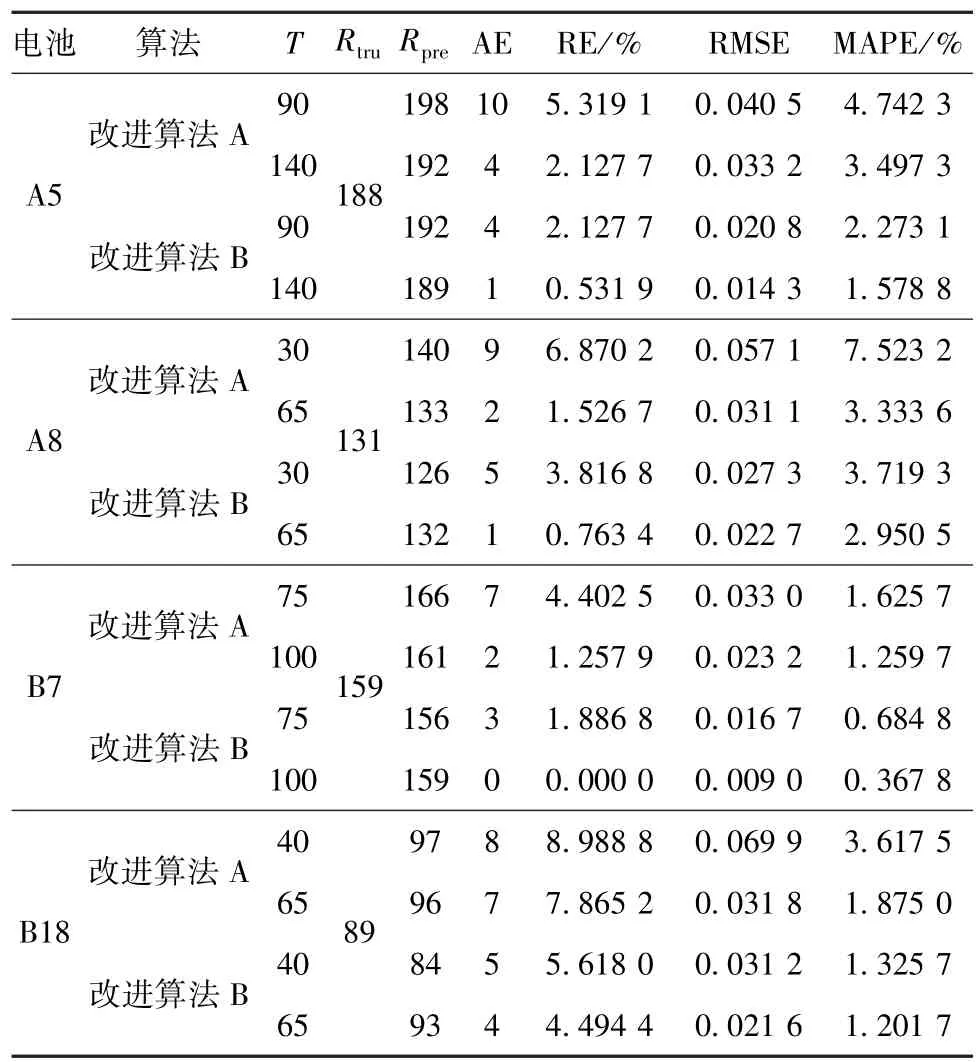
表4 不同預測起始點下的部分預測結果比較Table 4 Comparison of part of prediction results under different prediction starting points

從表4可知,隨著預測起始點的增加,兩種改進的算法的RMSE和MAPE值減小,且各自預測的RUL值也越接近真實值。當預測起始點為T=100時,對于B7電池,改進算法A、改進算法B的RMSE分別為0.023 2、0.009 0。

3 結論

本文作者重點關注輸入層與隱藏層之間的“局部”連接方式。改進算法A首先引進卷積、池化,改變了原有的全連接關系,神經網絡能夠學習局部相關性。該算法在減少參數冗余的同時,降低了計算量,可改善傳統ELM算法的大幅度發散效果,預測結果更為準確,誤差更小;但仍存在不確定性,預測結果并不理想。有鑒于此,改進算法B舍棄了卷積的操作,直接對輸入層數據進行池化,免去了參數的初始化以及激活函數類型的選取,算法的預測結果更穩定,魯棒性更強。

仿真結果表明:以B7電池為例,在不同的預測起始點下,改進算法A和改進算法B的均方根誤差在0.035以內,相比于其他ELM變形算法,具有較高的預測精度。而以B5電池為例,相比較于幾個典型的神經網絡,當T=90時,改進算法A和改進算法B的均方根誤差在0.030以內,且運行時間都不超過1 s。兩種改進算法在鋰離子電池的RUL預測中有很好的應用價值。