基于MPC 方法的風電場一次頻率協調控制策略

趙文欽，肖輝，樊國旗，林亞楠，文章

(1.長沙理工大學電氣與信息工程學院，湖南 長沙 410103；2.國網浙江省電力公司金華供電公司，浙江 金華 321001；3.湖南大學電氣與信息工程學院，湖南 長沙 410012；4.國網湖南省電力公司檢修公司，湖南 長沙 410004)

0 引言

近年來，傳統化石能源的大量消耗引起了全球對環境問題的廣泛關注，風能得到了快速發展。截至2019 年底，歐洲風力發電容量已達205GW:陸地183GW，海上22GW，占歐洲電力市場需求量的15%[1]。變速風力發電機接入電網數量增加，接口電力電子變流器具有輸出有功功率與系統頻率解耦的特性，導致系統頻率漂偏移增加。因此，世界各地的電網都對風電場在過頻和欠頻區域維持系統頻率穩定的能力提出了具體要求[2]。

目前，在系統頻率調節中引入風力發電的研究已經相當多。文獻[3] 驗證了通過短期從WTG中模擬傳統發電機特性的旋轉慣量或超級電容中釋放能量來實現一種虛擬慣量控制的方法。文獻[4] 通過在轉子側變換器的控制回路中添加一個頻率偏差項，將速度－轉子特性重新引入到變速風機中，仿真結果表明，這種控制策略下的低頻響應會提高轉子轉速，從而導致頻率突然下降。文獻[5] 提出了一種改進的風力發電機轉速下降控制策略，通過將脫線控制與臨時過度生產技術相結合，消除了頻率突然下降后的轉子加速相位。通過對葉片的俯仰或對機組轉子的過伸，可以實現脫油操作，該技術的具體實施方案在文獻[6－7] 中有詳細介紹。

除了基于局部控制器優化的控制策略外，還有一些基于優化策略的控制方法，可以實現每個風機之間的協作和交互。文獻[8] 在考慮風電場尾流效應的協調控制策略的基礎上，對每個機組的轉子轉速和槳距角的靜態參考值進行優化，以實現不同的運行模式切換。在文獻[9] 中設計了一種分布式牛頓方法，以實現稀疏通信網絡上風力發電機之間的快速協調。文獻[10] 提出了一種風電場參與一次頻率控制的模型預測控制方法，其中采用WTG 非線性動態模型來優化自身的動態行為。

本文提出了一種基于MPC 結構的數據驅動協調一次頻率控制新方法，該方法可以較好地解決實際中大型風電場中各WTG 參數難以測量和估值的問題。在該方法下，不需要周期性的模型參數維護，從而節省大量的時間和人力。仿真結果表明，該方法能使風電場在頻響過程中具有靈活的速度下垂特性，同時最大限度地減小轉子轉速畸變。

1 風力發電機模型

本文主要研究市場占比率較高的雙饋式發電機(Doubly Fed Induction Generator，DFIG) 型風力發電機(Wind Turbine Generator，WTG) 的建模與控制問題，其葉片捕獲機械功率如下:

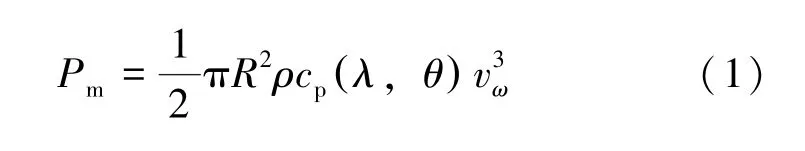
式中，ρ表示空氣密度，R表示葉片半徑，vω表示瞬時風速，cp表示風能轉換系數。風能轉換系數由葉片槳距角θ，葉尖速比λ決定，其中葉尖速比λ定義如下:

式中，ω為機械角速度。

將轉子軸的動力學模型簡化為一階慣性模型:

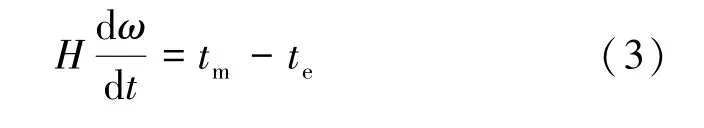
式中，H表示等效模型的旋轉慣量，tm和te分別表示機械轉矩和電磁轉矩。

為了保證轉子的轉速安全，在DFIG 的局部控制器中配置槳距控制器，可在高速風力條件下調節捕獲的機械功率。因其機械過程的特性，槳距調節器的響應通常較慢。

由于電氣控制和動態過程通常在瞬時完成，通常可被視作在一次頻率響應時間尺度下的靜態模型。

式中，Pe表示DFIG 的輸出有功功率，Pref表示輸入控制器的有功功率參考值。通過對轉子側變流器內電流控制回路的d－q軸分解，可實現DFIG 的有功和無功控制的解耦以及對局部下垂控制方法的適應。

DFIG 的實際動態行為應該包括整個控制過程中的通信延遲、計算精度和驅動動力學，這幾乎不可能通過經驗推導的方式準確建模。因此，在現有的數據測量、存儲和處理能力下，通過數據驅動的方法來揭示潛在的主導動態是一種更實用的方法。本文研究的一次頻率控制問題主要關注每臺WTG在頻率響應過程中的自身狀態穩定性。而轉子轉速穩定性則是最值得關注的控制指標。假設可測得瞬時風速與有功功率參考值，那么可以得到一個控制轉子轉速的WTG 離散動態模型:

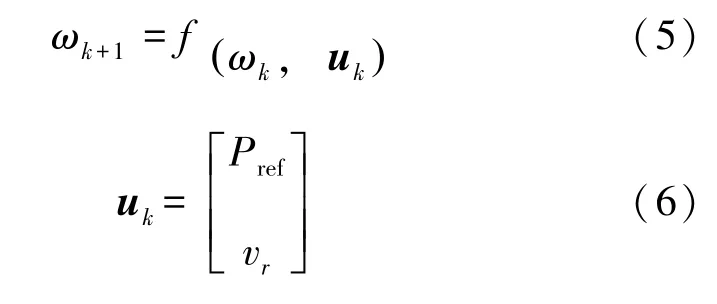
式中，f表示控制輸入以及狀態變量之間的耦合關系，uk為輸入控制矢量，由有功功率參考值和轉子轉速組成。

2 風電場控制策略

2.1 WTG 動態建模

由于控制輸入與狀態變量之間的動態耦合關系通常是非線性的，難以清晰地表達。實際應用中的解決方法是基于大數據集的移動快照對強耦合非線性關系進行局部線性化。設該對表示時間點k的擴展狀態，包括當前輸入和狀態變量，序列應該基于現有工作點獲取WTG 動態模型所需的信息。假設移動快照的長度為N，通過公式(7) 與(8) 對采集的數據局部線性化:

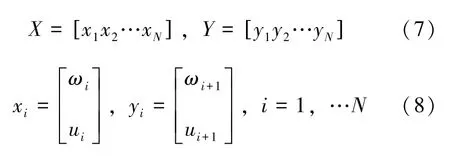
WTG 的線性動態模型可以表示為:

式中，S表示控制線性動態行為的矩陣。

S可由最小二乘法[11]解出:

式中，?代表矩陣X的偽逆矩陣。

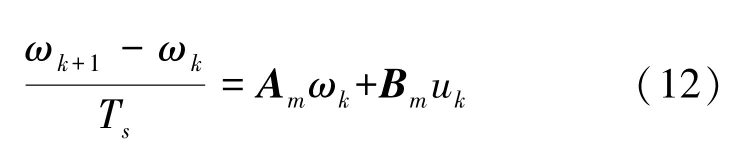
整理得到:

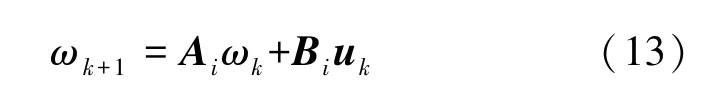
式中，Ai＝AmTs＋Ω，為離散系統矩陣；Bi＝BmTs，為離散輸入矩陣。

可以推出WTG 的控制模型:

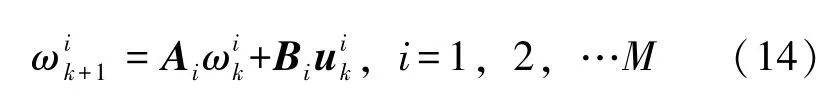
式中，M表示所控風電場中WTG 的臺數。

2.2 控制模型結構

基于WTG 的控制模型，定義中心狀態變量和輸入向量:

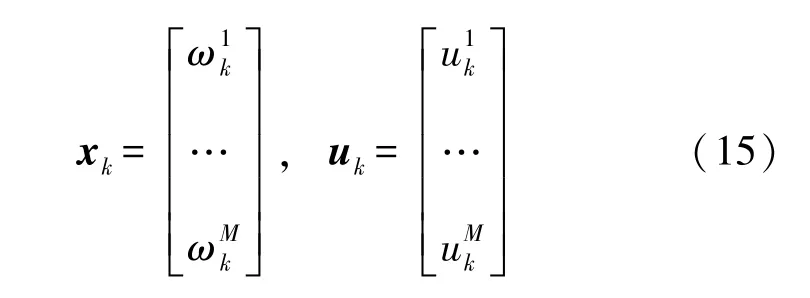
由式(15)，在單臺風力發電機組模型的基礎上，建立集中控制模型:

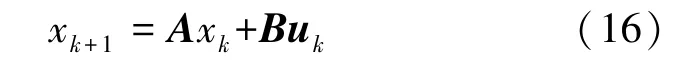
式中矩陣A和B由單臺WTG 的狀態轉移矩陣建立:

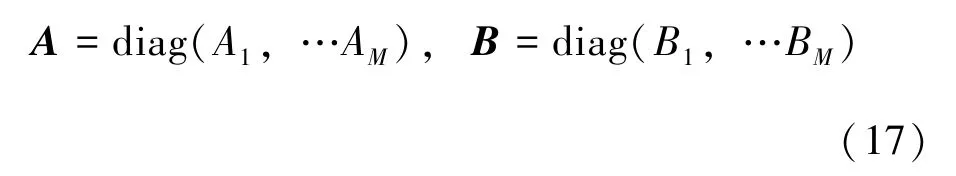
式(16) 即為整個風電場動態模型，為了實現一次頻率控制，穩定轉子轉速，提出MPC 控制方法:

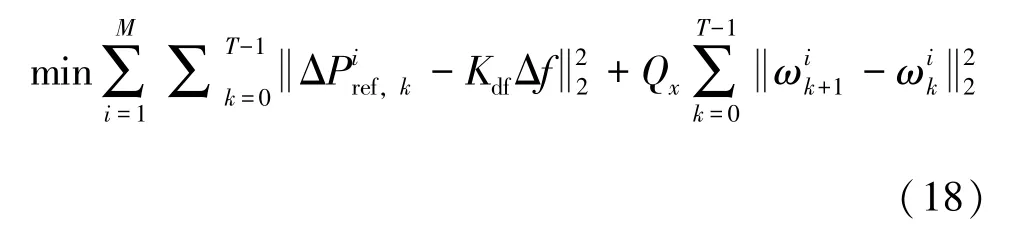
式中，Kdf表示速度下降率，Qx表示兩個控制目標之間的偏置系數，Δf為實際測得頻率fmeas與參考頻率fref的誤差:

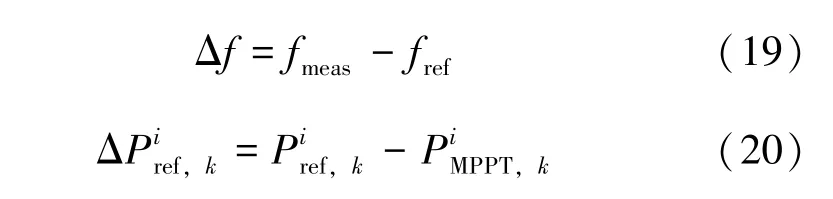
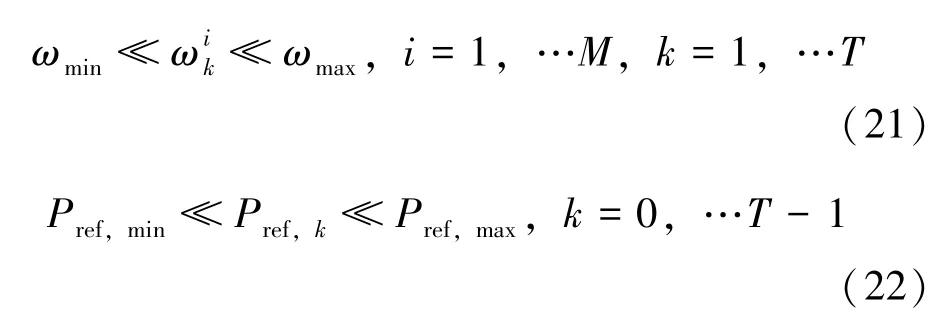
擬采用控制槳距角的方式調節有功，以實現頻率調節的目的，故還需設置WTG 的初始狀態:

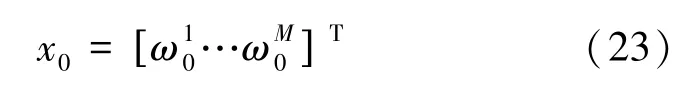
風機通過槳距角θ的變化獲得的有功功率P為:

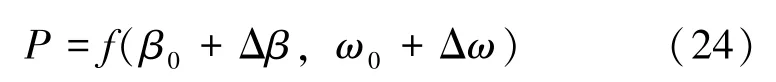
式中，β0、ω0分別為初始槳距角和轉子轉速，而系統實際槳距角由風機實際轉速與風機參考轉速的誤差值決定。

公式(18) — (24) 即為完整的風電場參與一次頻率控制過程的MPC 過程。

MPC 方法具體執行步驟如圖1 所示。

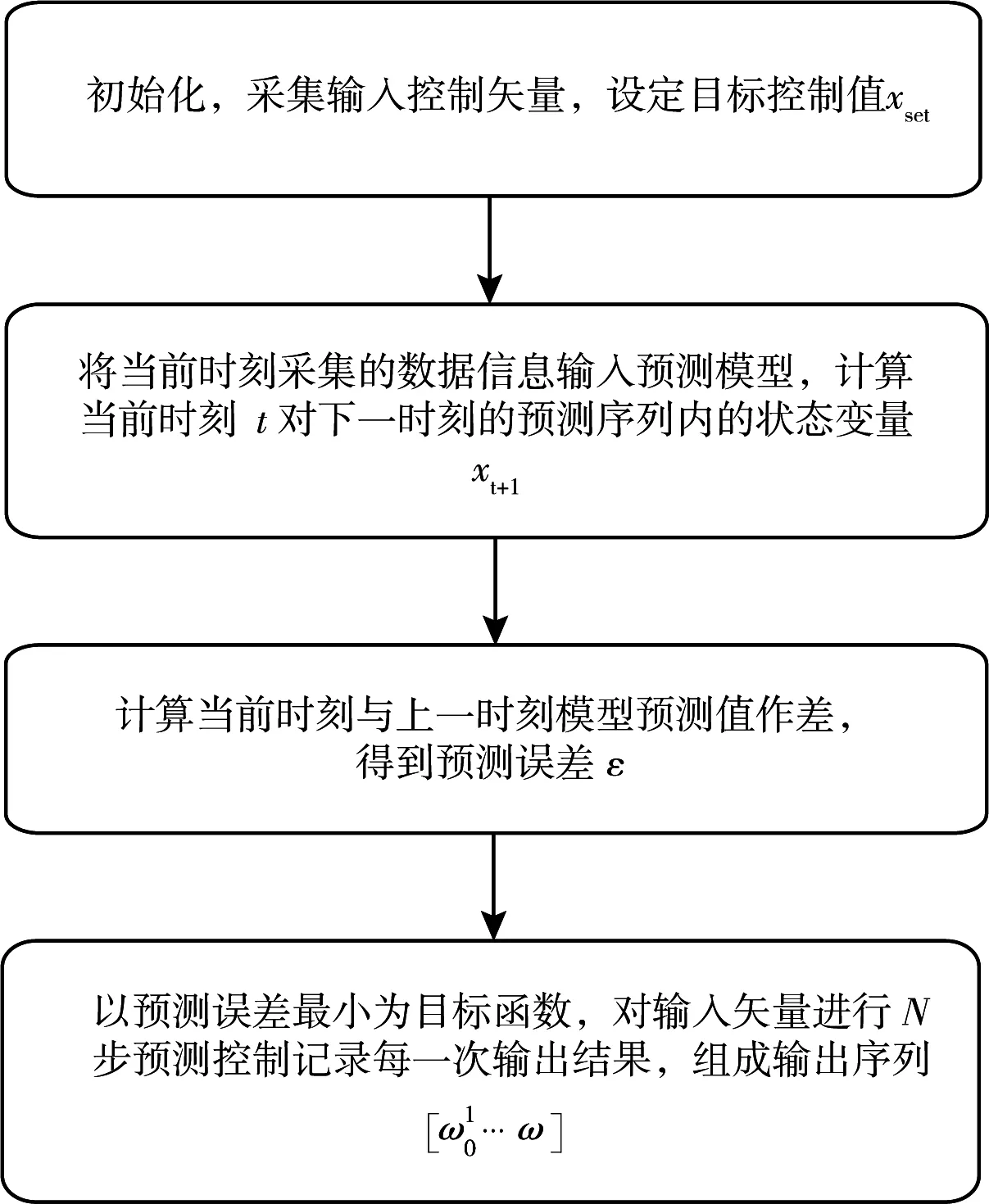
圖1 MPC 流程

3 DFIG－WTG 系統仿真模型

3.1 仿真模型建立

為了驗證所提方法的有效性，以IEEE9 總線系統為例，利用Matlab/Simulink 進行實例分析。圖2 所示的系統由三個集成的DFIG－WTG 組和兩個常規發電機組成。每組并聯50 臺容量為1.5 MW的WTG。兩臺同步機容量分別為250 MW 和200 MW。總能耗為315 MW，風電占比超過40%。考慮到一次頻率響應時間，將仿真時間設置為10 s，圖3 展示了此期間各機組風速變化情況。單臺WTG 模型和風電場控制器的詳細參數見表1。

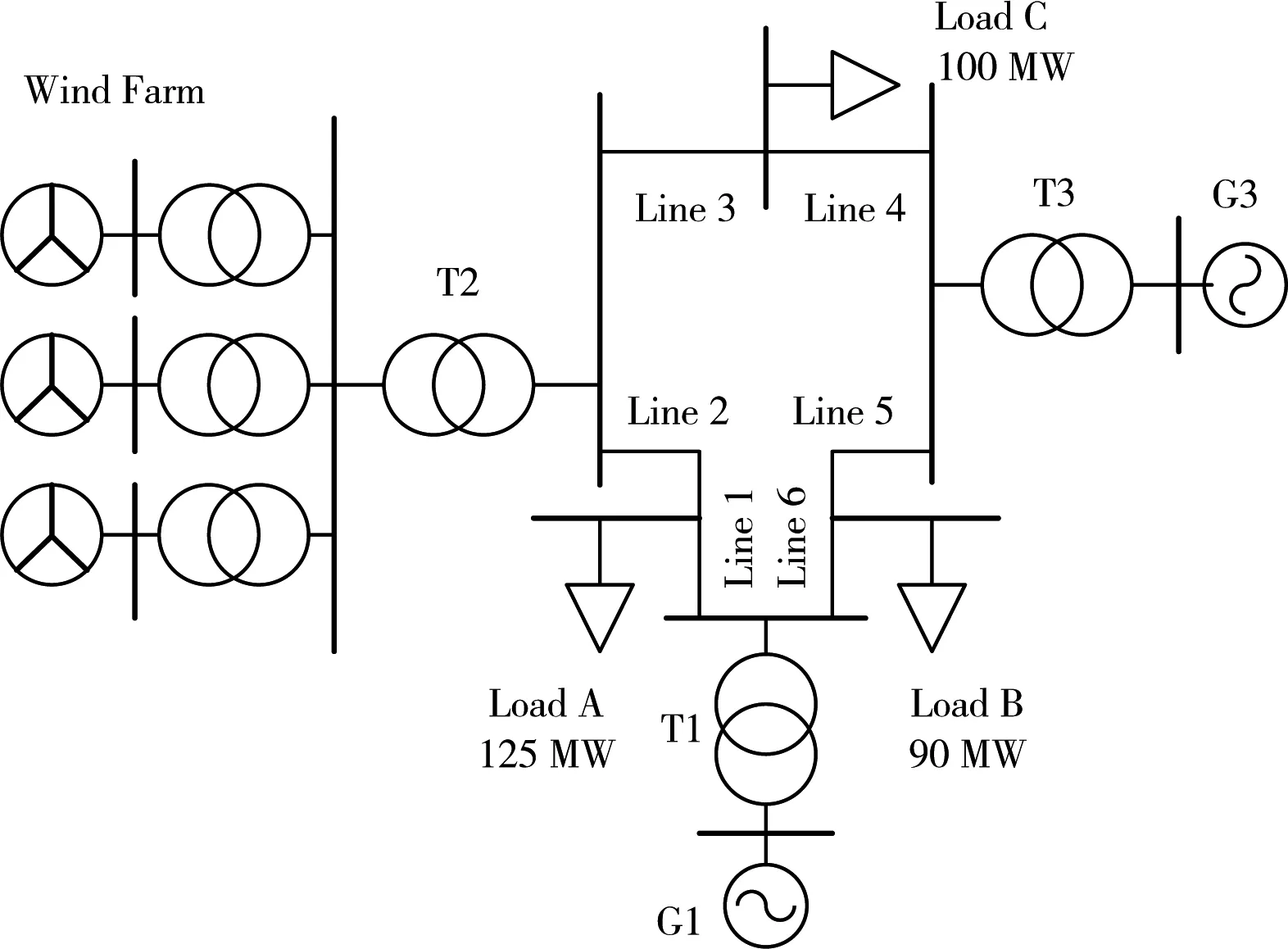
圖2 系統仿真模型

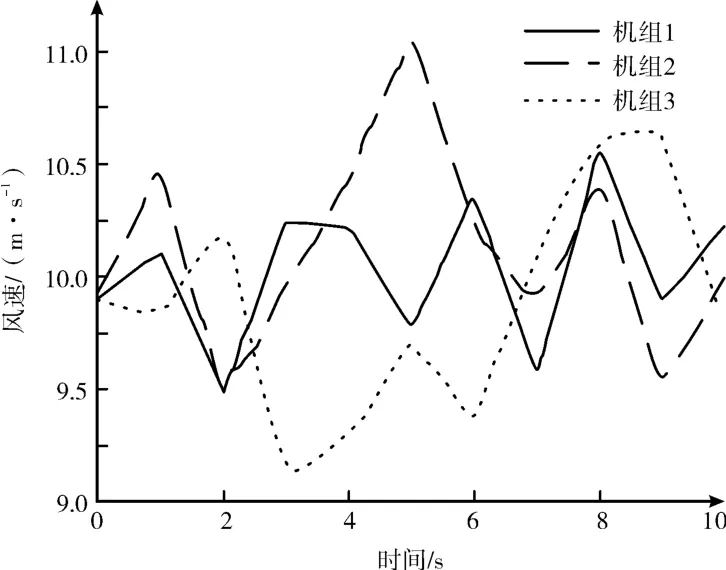
圖3 各機組風速變化圖

表1 風電場控制器與WTG 參數

3.2 低頻仿真分析

在MPC 策略基礎上，同時加入本地下垂控制(Local Droop Control，LDC) 策略。將負載波動設定為0.5 s，步長增加10%。在沒有風電參與頻率響應過程時，負荷波動會導致頻率嚴重下降至48.8 Hz 附近。為驗證所述控制策略，采取兩種不同方案進行對比。在方案一中，使MPC 控制器的速度下降率與LDC 控制器保持一致，調頻結果如圖4 所示。

可以看出，當風電參與調頻時，負荷波動引起的頻率偏移被限制在0.5 Hz 以內，避免頻率恢復過程中發生超調。MPC 策略下的頻率變化與LDC策略幾乎沒有差別。圖4 中整個風電場的輸出有功功率變化曲線也表明MPC 控制器與LDC 控制器具有相似的控制效果。這是因為MPC 控制器主要關注并追蹤系統操作者給出的速度下垂特性。

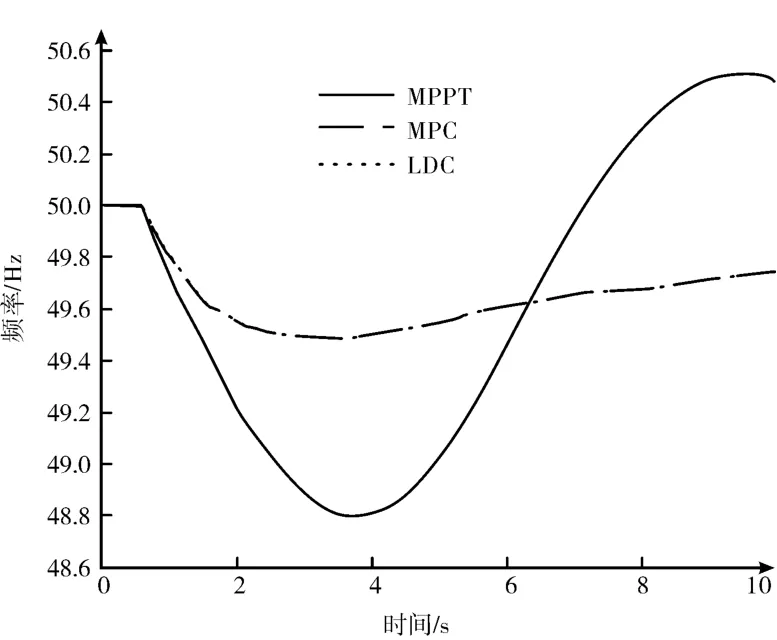
圖4 系統頻率變化圖(方案一)

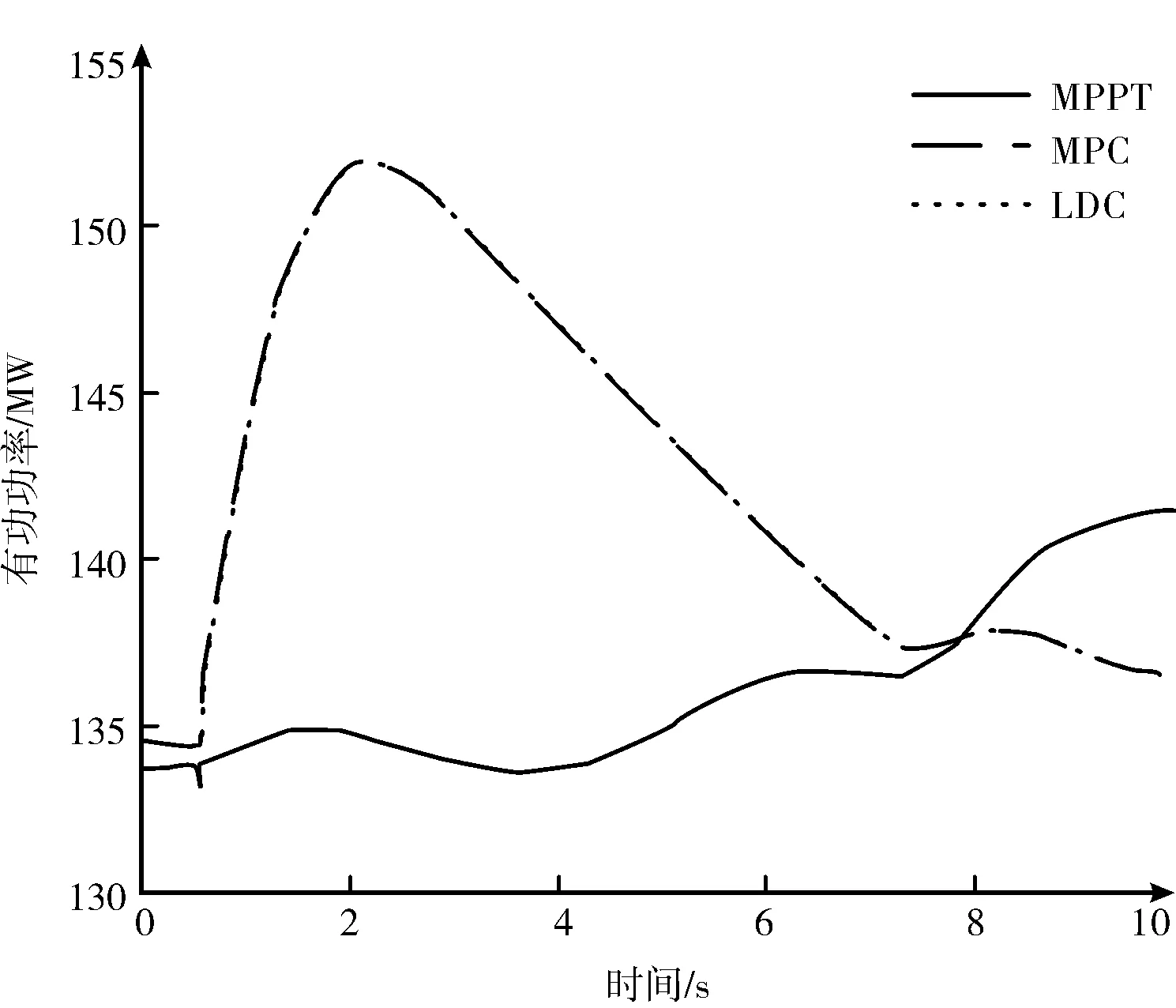
圖5 風電場輸出有功變化(方案一)

除頻率調節外，轉子轉速平滑下降是頻率控制過程中的另一個重點。在此，從整個風電場的角度定義轉子轉速畸變的平均水平:

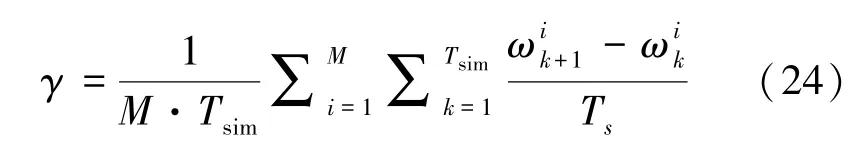
表2 中，風電場參與調頻使得轉子轉速變化顯著增加。但通過優化不同風速的WTG 機組的有功功率基準可以穩定WTG 轉子轉速，從而達到延長部件使用壽命的目的。MPC 控制器的平滑效果如圖6—8 所示。

表2 轉子轉速畸變率變化對比(方案一)

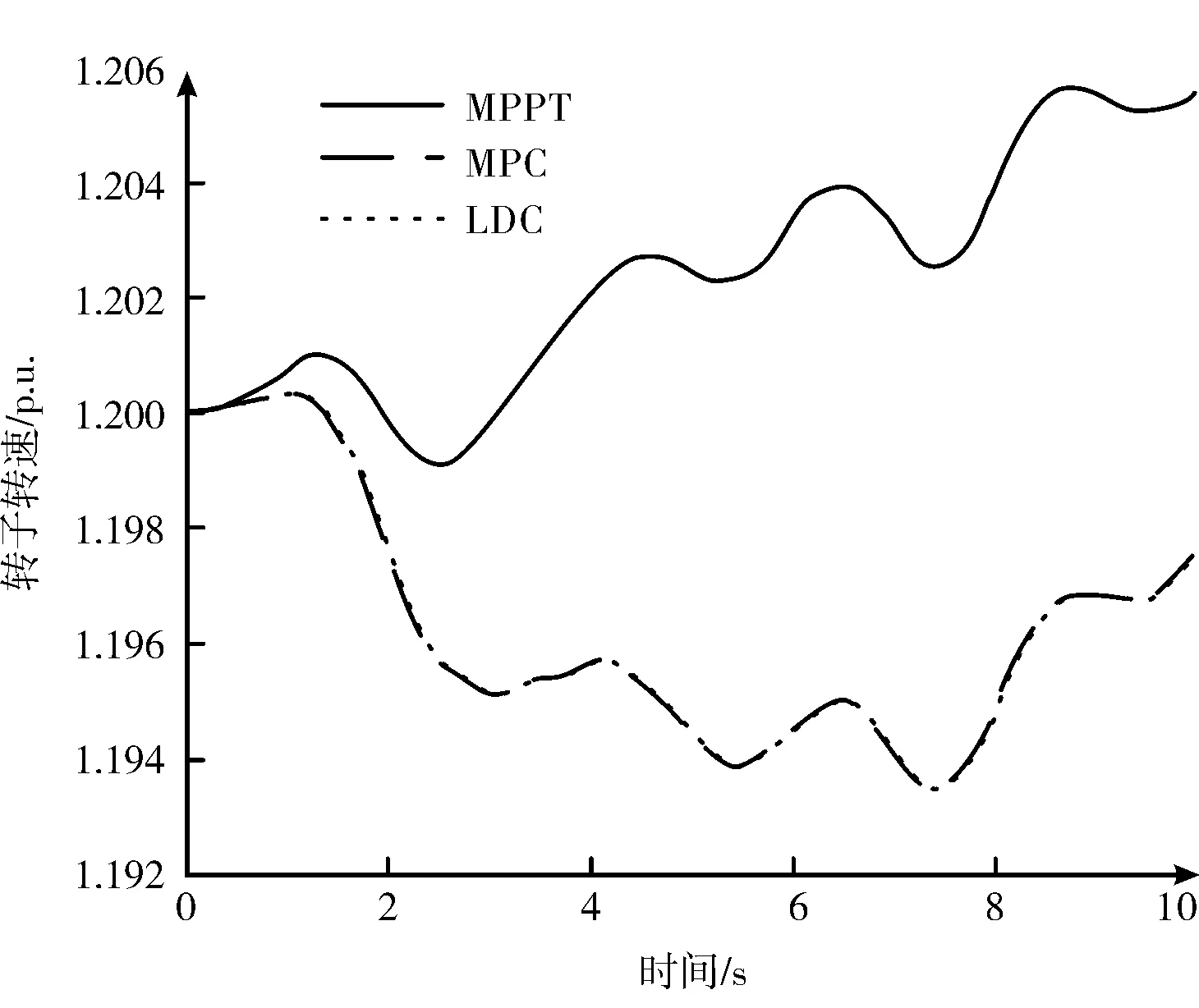
圖6 機組一轉子轉速變化圖(方案一)

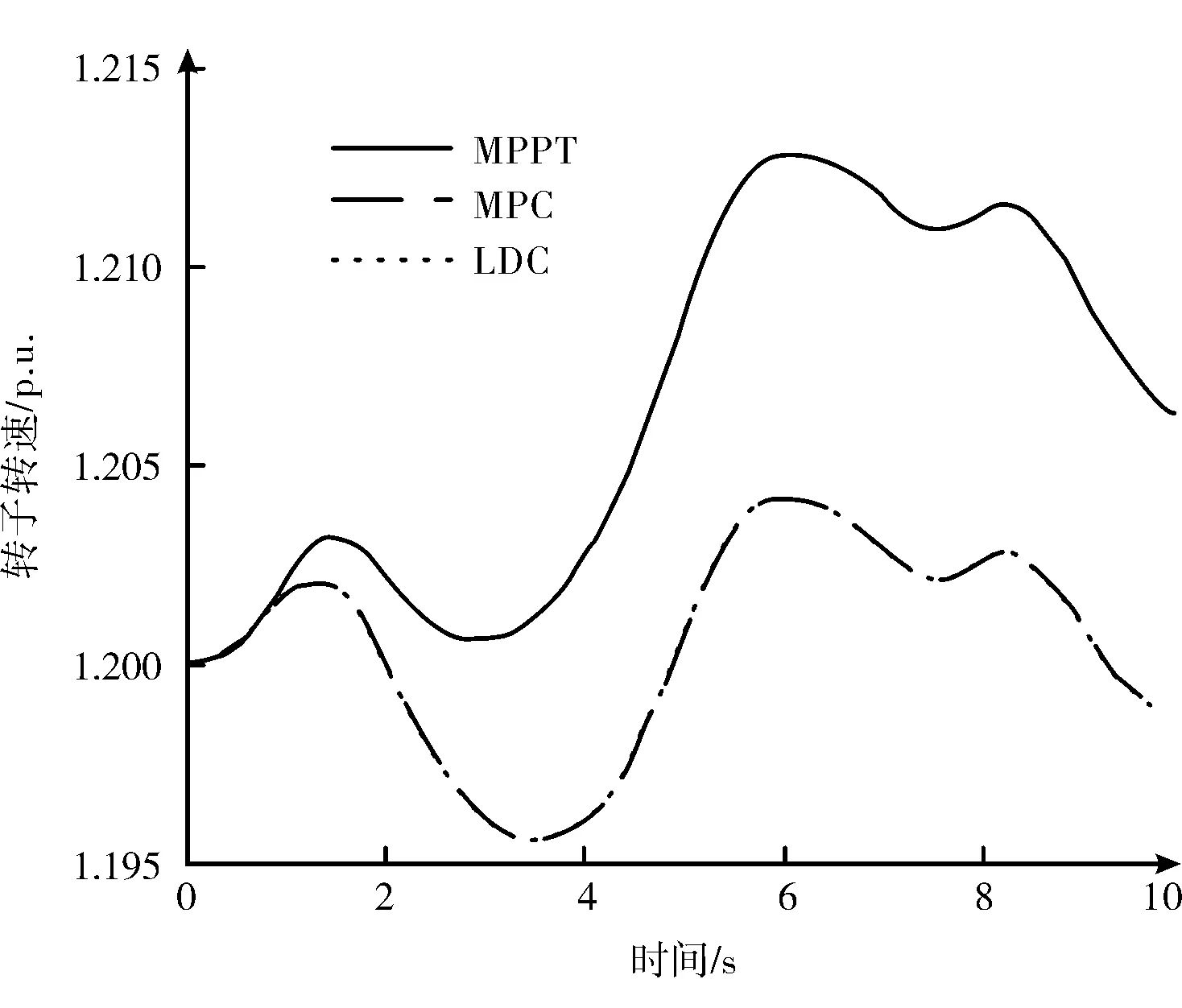
圖7 機組二轉子轉速變化圖(方案一)

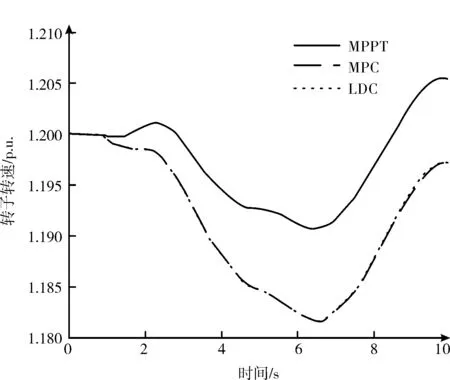
圖8 機組三轉子轉速變化圖(方案一)

3.3 下垂變化特性

協調控制策略的一個突出優點是風電場的下垂特性變化靈活，可以在短時間內通過調整局部控制器參數來改變該特性。

在方案二中，將速度下降率提高至0.3 p.u./Hz，圖9 表示相同負載條件下不同控制策略的結果。MPC 控制器使風電場參與調頻更加靈敏。因此，設置一個較小的頻率偏移值0.4 Hz，使其與電網要求的0.5 Hz 保持一定裕度。從圖10 可以看出，在協調控制模式下，風電場的參與可以使系統頻率更加穩定。上述結果表明，采用協調頻率控制策略的風電場能更加靈活地接受上級調度指令，與電網進行交互，同時有效地調整速度下垂特性。

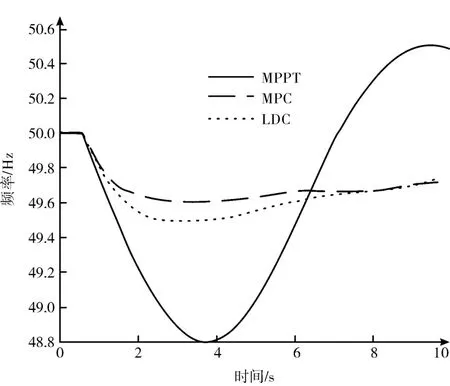
圖9 系統頻率變化(方案二)

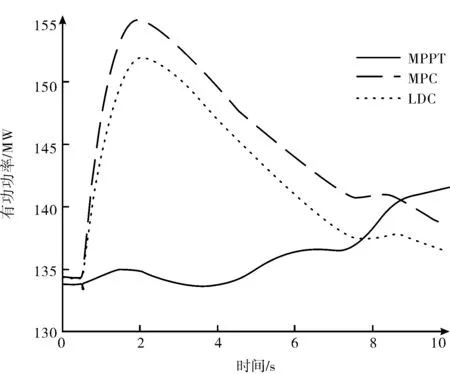
圖10 風電場有功輸出變化(方案二)

三組風機的轉子轉速變化情況如圖11—13 所示，轉子轉速變化情況見表3。可以看出，隨著轉速下降率增大，轉子轉速波動也隨之增大。各機組的平均轉速也因調頻過程的功率汲取而降低。考慮到風電場提供頻率調節服務的經濟效益，可以通過設置相應控制器來平衡增加的機械負荷。

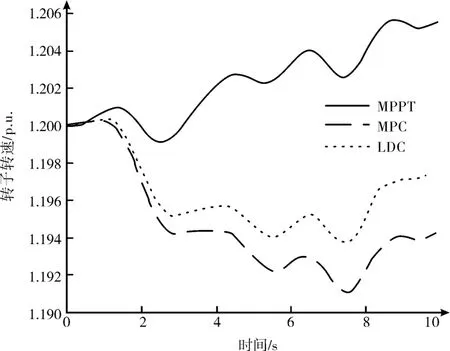
圖11 機組一轉子轉速變化圖(方案二)

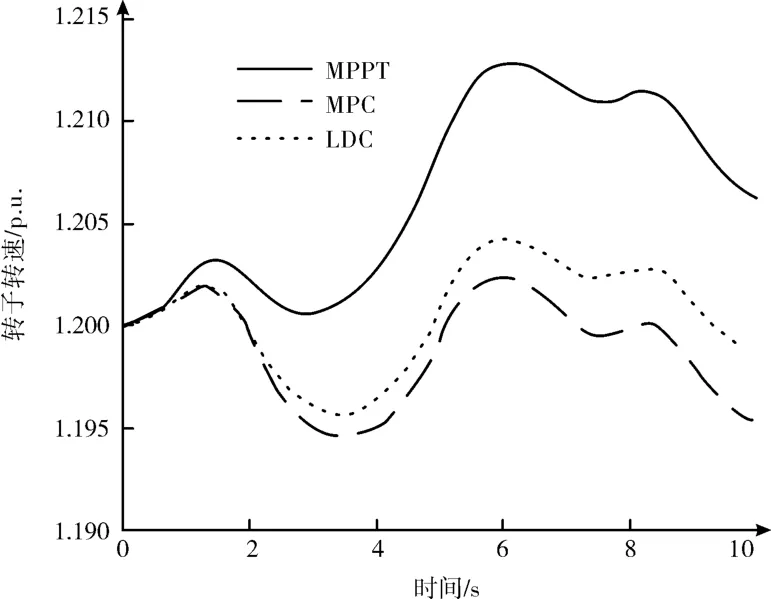
圖12 機組二轉子轉速變化圖(方案二)

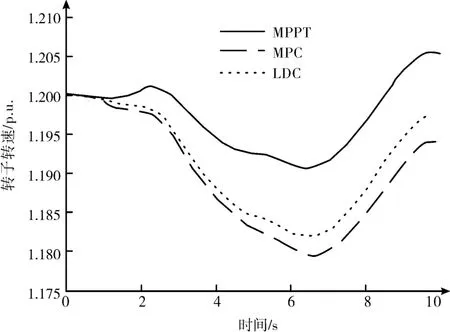
圖13 機組三轉子轉速變化圖(方案二)

表3 轉子轉速畸變率變化對比(方案二)

4 結論

提出一種基于MPC 方法的風電場頻率協調控制策略，該策略優化頻率響應過程中造成的轉子轉速畸變。該策略的優點主要有兩方面:利用不同工況下WTG 之間的相互作用平滑轉子轉速波動；具有靈活的速度下垂特性，響應迅速，滿足實際操作需求。仿真結果也驗證了風電場外部頻率響應與內部轉子轉速穩定性之間的平衡。