基于落角約束的偏置比例導引律的研究*

嚴鵬輝，劉剛，繆前樹

(中國直升機設計研究所，天津 300300)

0 引言

直升機機載反坦克導彈一直在反坦克作戰中發揮著重要作用。傳統的比例導引律雖具有控制簡單、過載變化小等優點，但是隨著坦克主動防御技術的完善,以及正面和側面裝甲防護的加強，此時通過增大導彈落角并且控制落角精度來攻擊坦克防護薄弱部位(如炮塔頂部等)宜為一種較理想的毀傷方式[1]。

對于導彈飛行末端帶落角約束制導律的研究，主要是基于比例導引律的改進并結合現代控制理論形成約束條件[2-4]。影響導彈落角的方式有多種，如導彈初始高度、彈目距離等[5-6],而對導彈導引律的設計是最為關鍵的措施[7]，如王利芳等[6]、林德福等[8]通過在導引律中添加重力補償項，可以增大導彈的命中落角，但是落角提升的幅度有限，而且難以做到落角的精確控制。Zarchan[9]利用Schwartz不等式推導出彈道成型最優制導律，在控制能量消耗需求最小的同時，實現了落點與落角的雙重約束；Ratnoo[10-11]對傳統比例導引進行擴展變形，得到基于落角約束的兩段變增益比例律;王廣帥[12-13]將常值偏置項添加到比例導引律中，可以實現對目標的落角約束;高峰[14]對導引律做微分處理，提出一種基于落角約束的偏置比例導引律。

本文基于彈目碰撞三角形關系，借鑒文獻[13,15-16]思想，考慮目標速度方向，研究了基于落角約束且無需精確計算剩余飛行時間的變增益偏置比例導引律；同時與彈道成型制導律、兩段變增益比例導引律進行比較，分析三者彈道曲線、傾角、過載和控制能量消耗的區別；給出不同初始條件,進一步探究此制導律性能，對比了不同落角約束對導彈彈道、過載和控制能量消耗的影響。

1 彈目相對運動模型

如圖1所示，M和T分別表示導彈和目標，vM，vT分別為導彈和目標速度矢量，與x軸方向夾角分別為θM，θT。vR為相對速度矢量，θR為相對速度矢量與x軸夾角，r為彈目距離，q為彈目視線角。為研究方便，本文中將角度的正方向定義為逆時針方向。

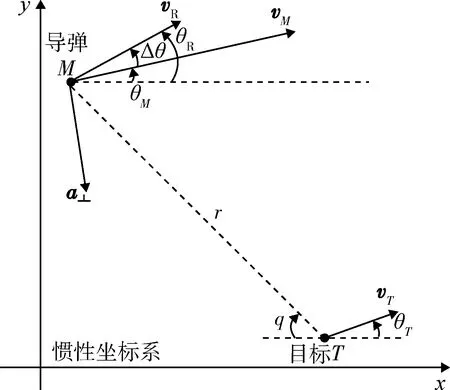
圖1 彈目相對運動幾何關系Fig.1 Relative motion geometry between missiles and targets

根據彈目相對運動關系有

vR=vM-vT,

(1)

在x向和y向投影分別有

vRcosθR=vMcosθM-vTcosθT,

(2)

vRsinθR=vMsinθM-vTsinθT.

(3)

假設vT速度恒定，且實際情況下反坦克導彈速度vM遠大于vT，因而θT的改變可認為對導引律的影響忽略不計，將式(2)和(3)進行微分處理后有

(4)

(5)

(4)×cosθR+(5)×sinθR得到

(6)

(4)×sinθR-(5)×cosθR得到

(7)

另外彈目相對運動微分方程有

(8)

(9)

用Γ表示導彈落角，有Γ=θM-θT，如圖2所示。根據彈目碰撞三角形關系有

(10)

由正弦定理可以得到

Δθ=arcsin(sin ΔvT/vR).

(11)

進而得出導彈落角Γ與θR關系有

θR=θT+Γ+Δθ.

(12)

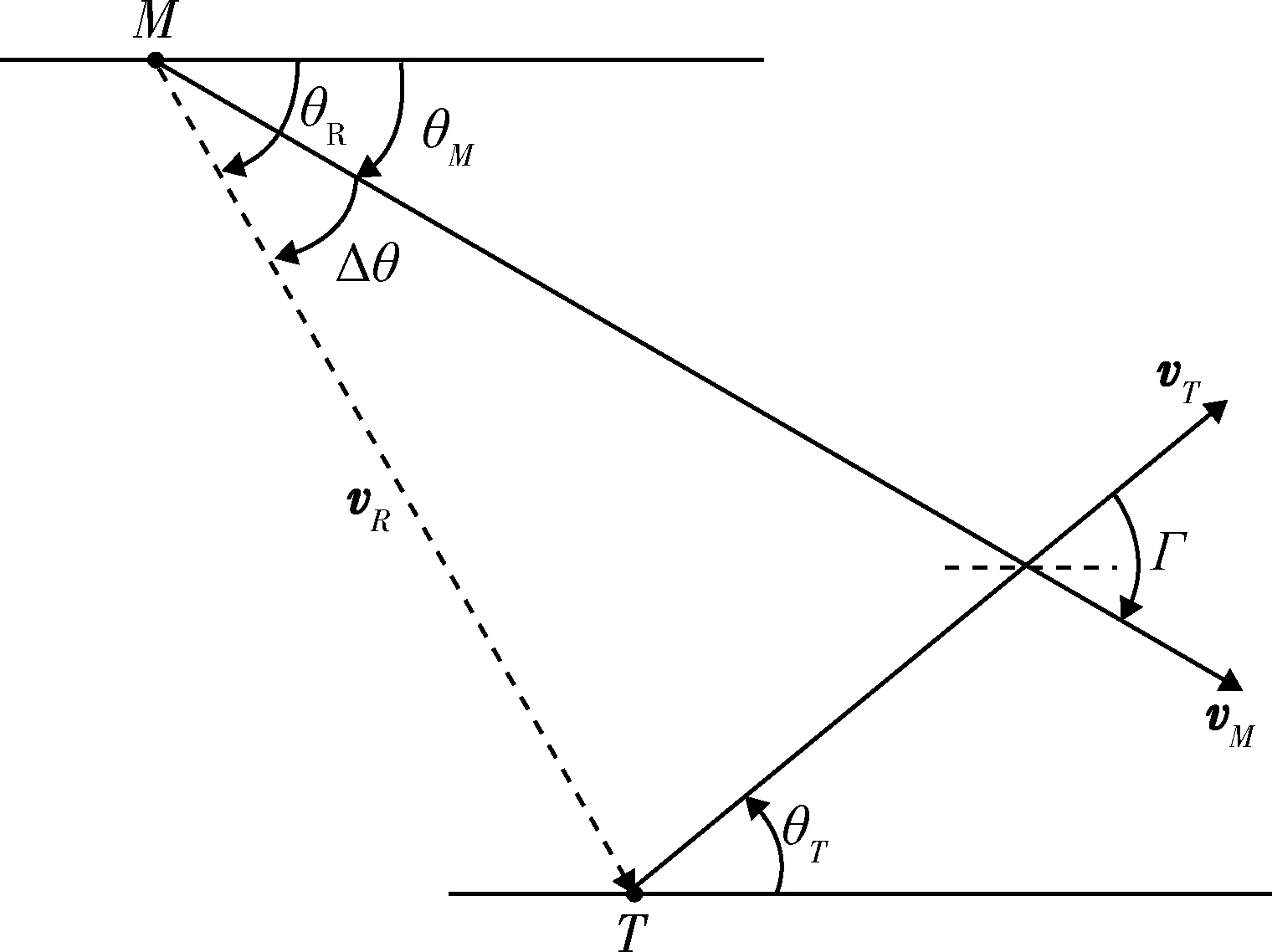
圖2 彈目碰撞三角形圖Fig.2 Collision triangle diagram between missiles and targets

2 偏置比例導引律的設計

彈目相對運動形式的導引律為

(13)

式中：k為比例導引系數；b為偏置項。

(14)

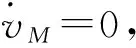
(15)

對式(13)兩邊積分有

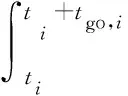
(16)

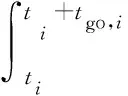
Bi=kqi+(1-k)θR,f-θR,i.

(17)

相應地對式(12)在終端tf時刻有Δθf=arcsin(sinΓ·vT/vR,f)即

θR,f=θT+Γ+Δθf.

(18)

代入式(17)有

Bi=kqi+(1-k)(θT+Γ+Δθf)-θR,i.

(19)

對于剩余飛行時間可以作近似估計

(20)

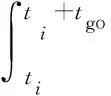
(21)

可以近似得到

(22)

3 仿真分析

3.1 不同導引律對比分析

為便于對比分析此導引律性能，選取彈道成型制導律[9]、兩段變增益比例導引律[11]進行仿真分析對比，兩者的形式如下：

(23)

(24)

式中:λ由文獻[11]給出：

(25)

同時,為研究導引律的能量需求，引入控制能量消耗

(26)

仿真基本參數如下：導彈初始位置M(0,200)，速度vM=300 m/s，目標初始位置T(2 500,0)，速度vT=20 m/s。此偏置比例導引律的比例系數選取k=3，設置三者期望落角均為Δ=-60°，θM0=30°，θT0=30°。利用Matlab/Simulink軟件，設置當彈目距離r<0.1 m時計算停止。

仿真結果如表1和圖3所示。仿真圖表中以BPNG表示落角約束的偏置比例導引律，KPNG表示兩段變增益比例導引律，OPNG表示彈道成型導引律。

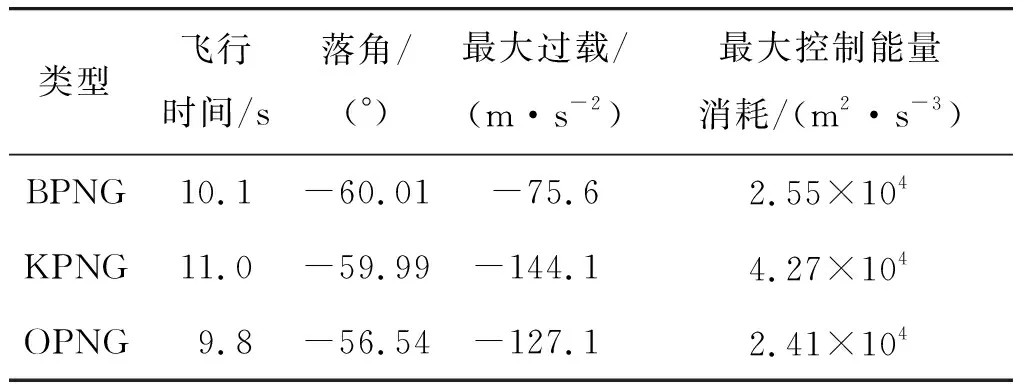
表1 不同導引律對同一目標計算結果(Δ=-60°)Table 1 Different guidance laws calculation results for the same target (Δ=-60°)

通過表1可以看出,BPNG與OPNG飛行時間接近，較KPNG約有1 s差異；對導彈最終落角進行比較，BPNG與KPNG對導彈落角控制精度較好，OPNG與期望落角誤差偏大；另外BPNG最大過載遠小于KPNG和OPNG，結合圖3b)可以看出KPNG過載有跳變現象，最大值出現在制導指令切換時刻；全過程累積控制能量消耗BPNG與OPNG接近，且小于KPNG。

從圖3a)的彈道曲線可以發現，3種導引律均通過調高初始攻擊段彈道弧度來實現增大導彈落角的目的，在滿足落角約束的前提下KPNG彈道爬升幅度最大，BPNG和OPNG彈道收斂更快；對3種導引律法向過載分析如圖3b)所示，BPNG的法向過載變化范圍最小，OPNG命中時刻的過載最大，而KPNG過載變化中有明顯的跳變，此時制導指令改變，法向過載最大值出現在此時刻，此后過載逐漸減小；分析三者導彈傾角變化如圖3c)，傾角均由初始傾角30°逐漸減小到預設期望落角值，BPNG和OPNG曲線變化相似，而KPNG曲線分2段，前期緩慢減小，制導指令切換后以較快速度改變至期望落角值；對三者控制能量消耗曲線對比分析如圖3d)，BPNG和OPNG曲線平緩增加，而KPNG在制導指令切換后急速增大。

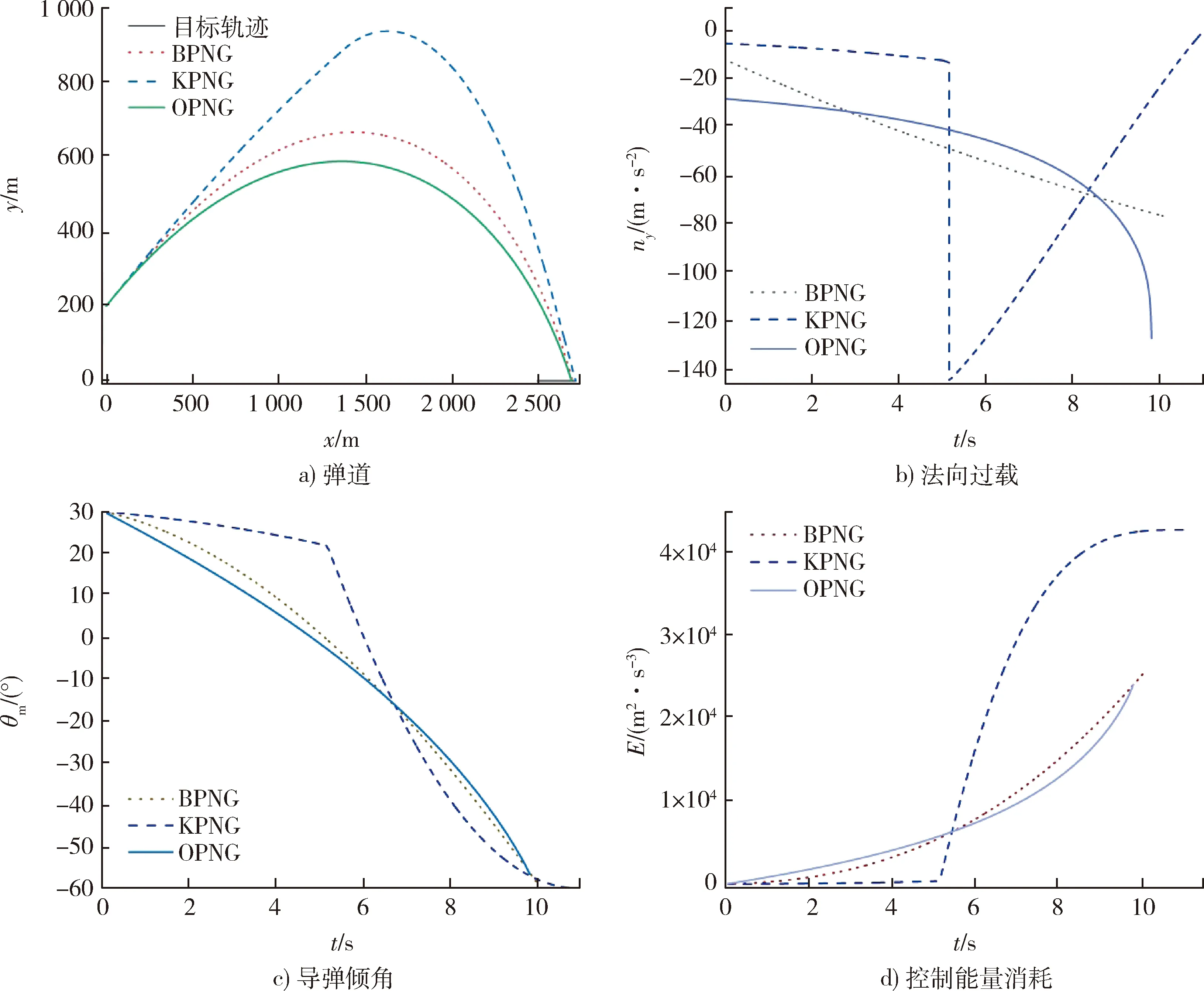
圖3 落角約束Δ=-60°下3種制導律下對比圖Fig.3 Comparison of three guidance laws under impact angle constraint for Δ=-60°

綜合進行考慮，KPNG和BPNG落角精度較高，但KPNG彈道高度較大，且比例系數轉換后導致過載有跳變，進而引起控制能量消耗的急速增大，對導彈載荷設計以及燃料攜帶有更高的要求；對于導彈末端過載和落角誤差，OPNG相對BPNG偏大，可見BPNG的制導性能相對較好。

3.2 偏置比例導引律性能研究

為充分分析BPNG的制導性能，給定不同初始條件進行仿真分析，結果如表2所示。可以看出，此制導律有較高的制導精度。如圖4所示，隨著期望落角約束的增大，導致彈道的初始爬升高度會增大，以獲取更大的終端落角。結合圖5和圖6不難看出，導彈過載和控制能量消耗有較大改變。可見，落角約束并不是越大越好，根據目標類型的不同可以選取不同的落角約束。如坦克等重裝甲目標可以適當增大落角約束，如步兵車等輕裝甲車等可以適當減小落角約束。

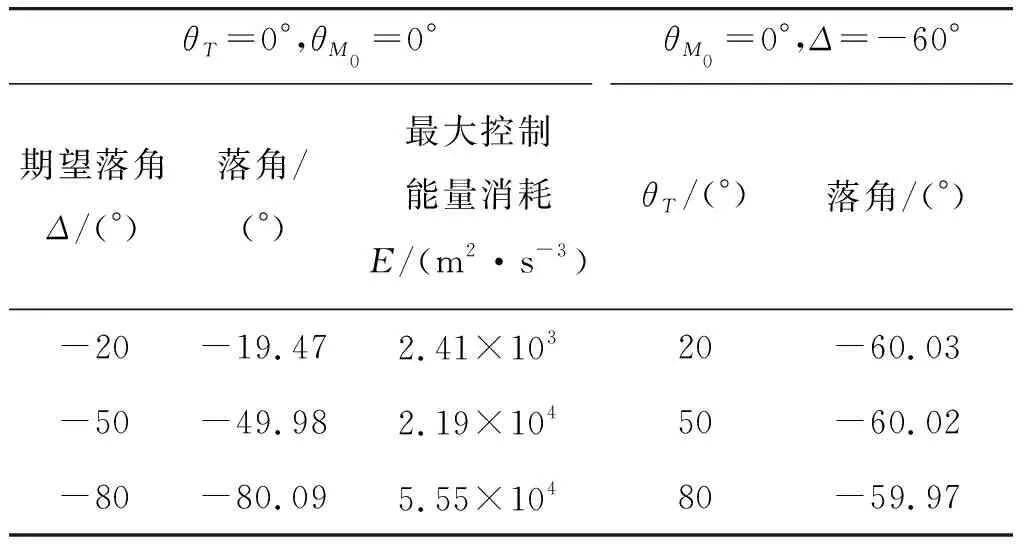
表2 不同初始條件下的仿真結果Table 2 Simulation results under different initial conditions

為探討此導引律在飛行過程中制導指令的切換，圖7給出了不同落角約束下的偏置項和彈目視線角速率隨時間變化曲線。從中可以看出，此偏置比例導引律初始導彈爬升階段主要起到制導指令作用的為偏置項b，之后隨著b的逐步減小，彈目角速率逐漸增大，比例項對制導指令起到主導作用。落角約束越大，需要的偏置項b也隨之增大，彈目角速率改變也更快。結合圖4可以看出，該制導方案能夠保證導彈在末制導前期利用偏置項b進行彈道爬升，中后期利用比例項來完成落角約束時也保證彈道的收斂。

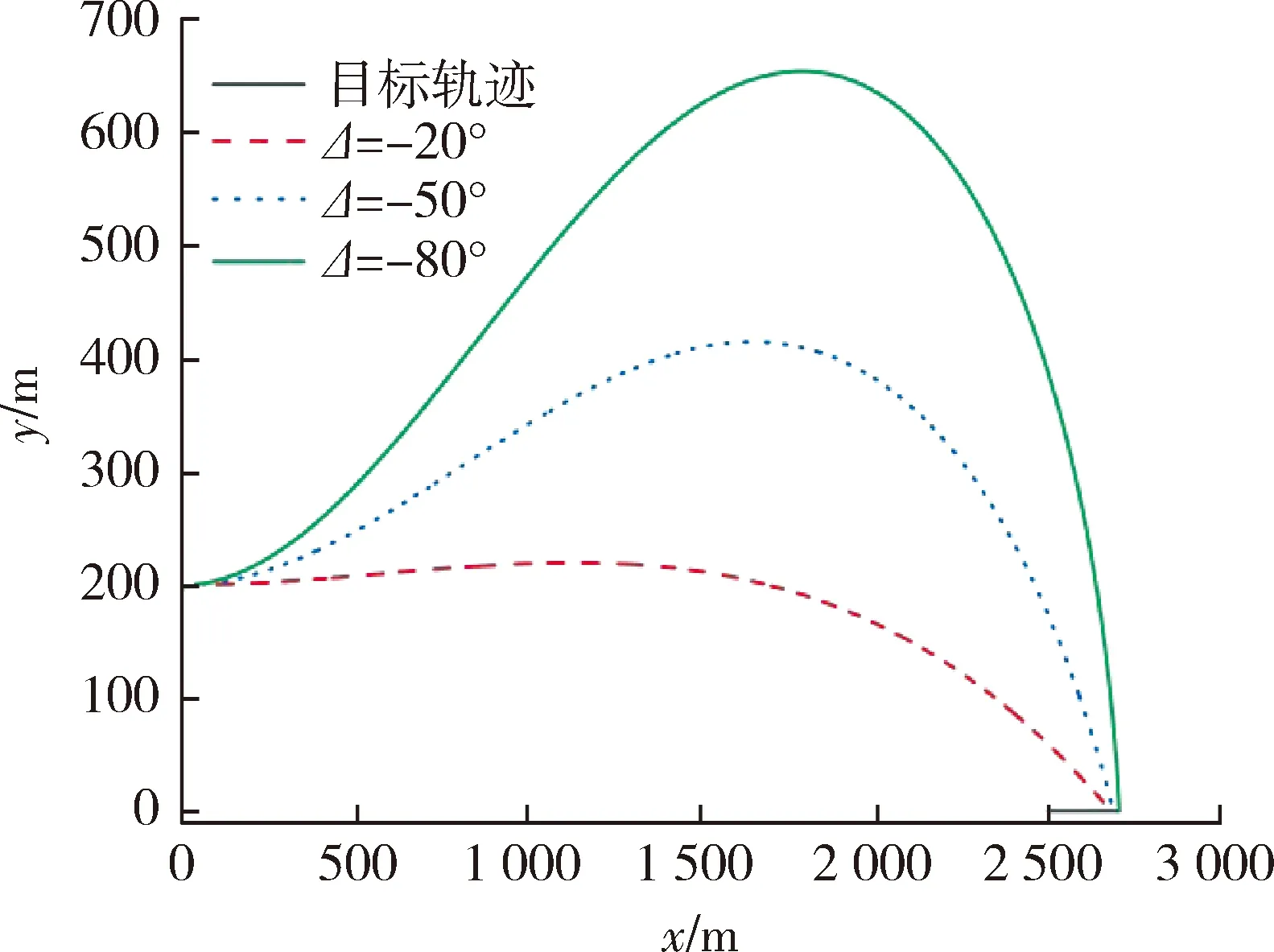
圖4 不同落角約束下的彈道曲線Fig.4 Ballistic curve under different impact angle constraints

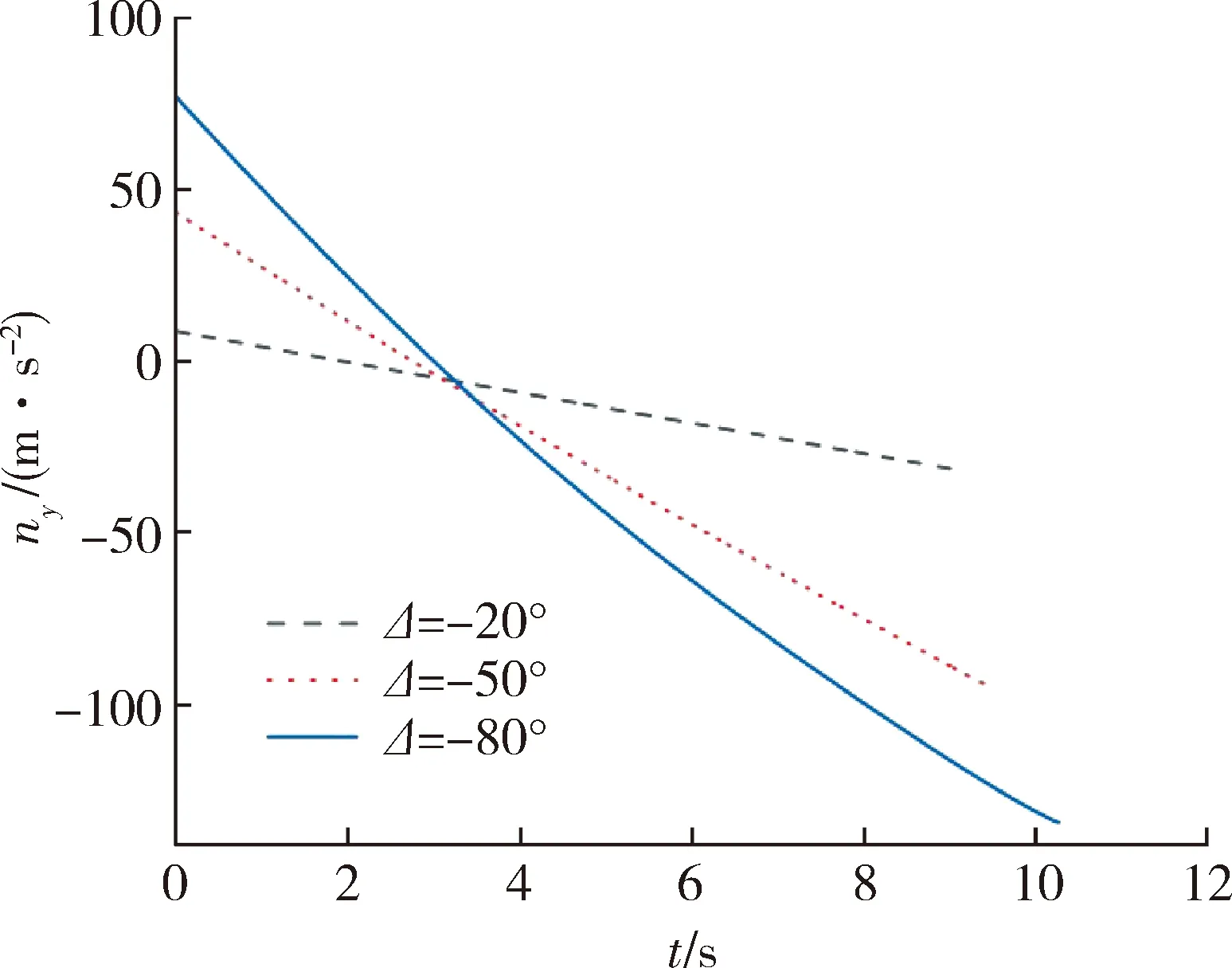
圖5 不同落角約束下的法向過載曲線Fig.5 Normal overload curve under different impact angle constraints

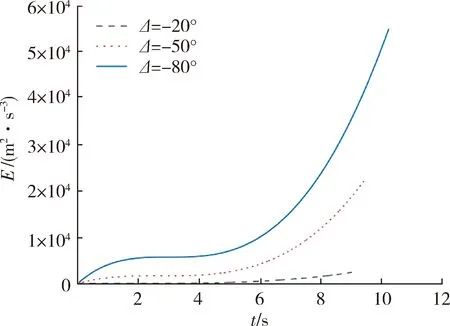
圖6 不同落角約束下的控制能量消耗曲線Fig.6 Control energy consumption curve under different impact angle constraints

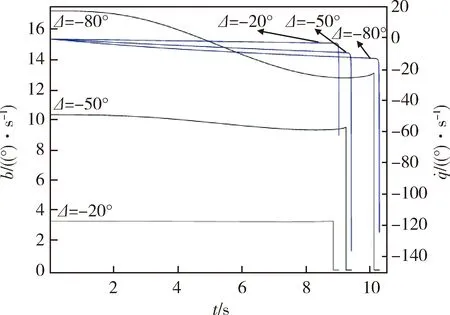
圖7 不同落角約束下的偏置項和 彈目視線角速率變化曲線Fig.7 Bais and line-of-sight angular rate curve under different impact angle constraints

4 結束語

精確控制反坦克導彈的終端落角，對于目標毀傷具有重要的意義。本文通過彈目碰撞三角形關系，探究了彈目相對速度與落角約束之間的關系，進而給出了基于落角約束的變增益偏置比例導引律的關系式。通過與彈道成型制導律和分段變增益比例導引律對比，此導引律具有較高的制導精度，同時過載變化和控制能量消耗均較小。另外，計算表明，此制導律可滿足不同仿真條件并具有較高的精度，但隨著落角約束增大，導彈過載和控制能量消耗變化相應加劇，表明落角約束不是越大越好。最后進一步探討此導引律的各項系數對彈道的影響，對偏置項和彈目視線角速率變化分析表明，初始階段偏置項起到制導指令主導作用，彈道爬升，后續比例項對制導指令起主要作用，完成落角約束同時也保證了彈道的收斂。

本文的制導方案在滿足落角約束的同時無需精確計算剩余飛行時間，提高了導引律的實用價值，可為直升機機載反坦克導彈制導律的設計提供參考。