基于數值仿真的大型薄甲板總段吊裝方案設計優化

魏 波， 步林鑫， 張莉莉， 王 樂

(江南造船(集團)有限責任公司，上海 201913)

0 引 言

在船舶建造總段吊裝過程中，由于受到結構自重和鋼絲繩拉力作用，船體結構會產生變形和應力集中現象，在嚴重時可能出現結構塑性變形甚至結構破壞，從而為船舶安全生產帶來較大的風險[1]。

在產品總組階段，吊裝結構多為大型總段，而多數總段吊裝甲板面出現厚度較小、自重較大的情況，統稱該類總段為大型薄甲板總段。該類總段吊裝甲板區域面積大且板厚薄，多為5.0～6.0 mm，總段質量多在500 t以上，最大超過1 000 t。

基于上述較為極端的結構形式，應考慮盡可能增多吊碼數量，吊碼應布置在構件區域，有效傳遞吊碼所受拉力。由于大多數吊碼反面骨材規格較弱，在總段吊裝過程中難免產生各類風險。因此，考慮在總段吊裝前，建立大型薄甲板總段有限元模型，模擬吊裝過程，迭代優化吊裝方案，保證總段吊裝安全順利實施。

1 數值仿真與優化流程

數值仿真技術模擬總段吊裝過程，不僅可直觀地反映在總段吊裝過程中各構件變形情況，而且可較為準確地反映總段各區域應力分布情況，找到應力集中區域，進行有針對性的加強，反復迭代和優化，從而保證在總段吊裝過程中各結構應力及變形皆小于許用值。總段吊裝數值仿真及優化流程[2]如圖1所示。

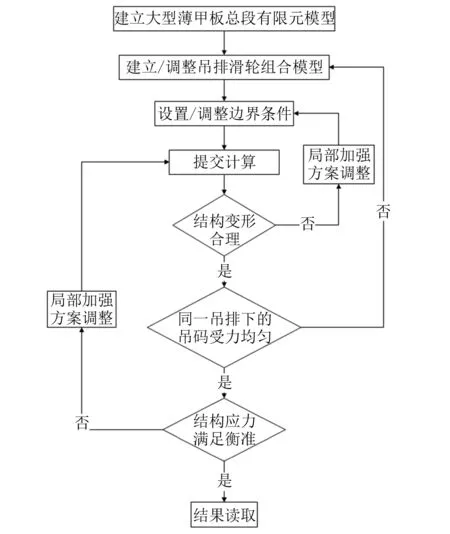
圖1 總段吊裝數值仿真及優化流程

值得注意的是：現場門式起重機在起吊后具有自平衡的過程，即同一起吊小車下的吊排及吊碼的受力應當均勻，由于摩擦力的存在，雖不能使所有吊碼受力完全一致，但誤差應較小。在數值仿真流程中建立/調整吊排滑輪組合模型的過程可確保各吊碼的受力均勻。

2 吊碼布置與加強方案

總段吊裝吊碼布置方案可根據現場門式起重機具備的起吊能力及鉤數、總段質量、單個吊碼承載能力、吊裝甲板構件分布等情況確定，吊碼布置在結構區域。薄甲板總段有限元模型如圖2所示。總段吊裝甲板面吊碼布置情況如圖3所示。根據總段各要素確定該總段吊碼數量為左右舷各16個，通過數量較多的吊碼可有效將總段質量分散承擔，并將拉力傳遞至甲板反面的構件，以此緩解構件承受的應力。

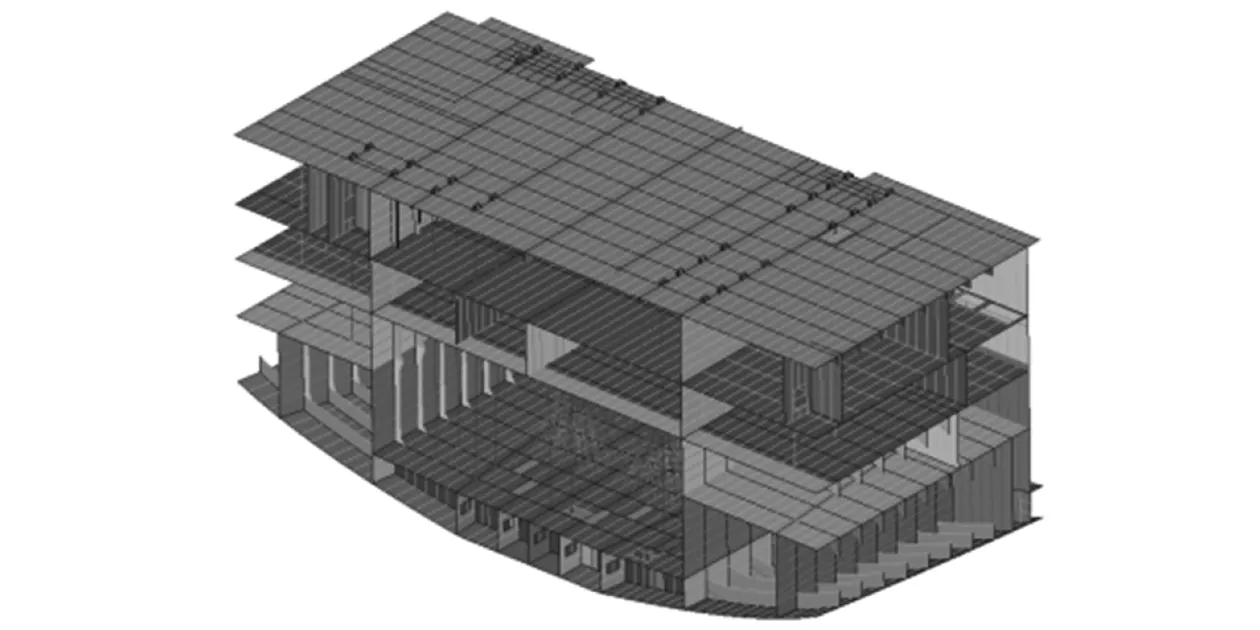
圖2 薄甲板總段有限元模型

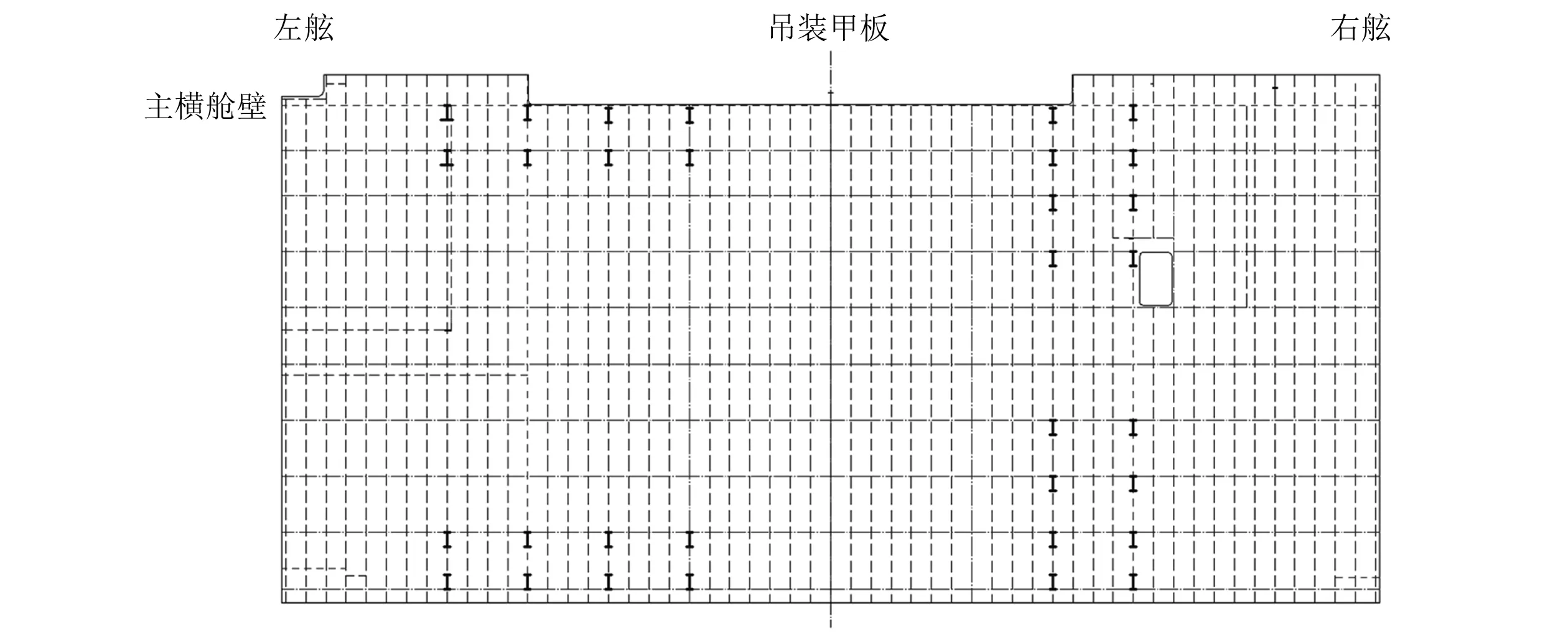
圖3 總段吊裝甲板面吊碼布置示例

考慮吊碼反面的縱骨相對較弱，且總段整體質量較大，整個吊裝系統的加強方案原則如下：(1)在吊碼下方和多層甲板間布置槽鋼、合抱槽鋼，以加強結構、傳遞拉力，如圖4所示；(2)若吊碼橫向布置，且反面無強結構，則反面布置橫向加強板，設置槽鋼與下層甲板連接，如圖5所示；(3)部分角隅、硬點位置增加加強板，如圖6所示。

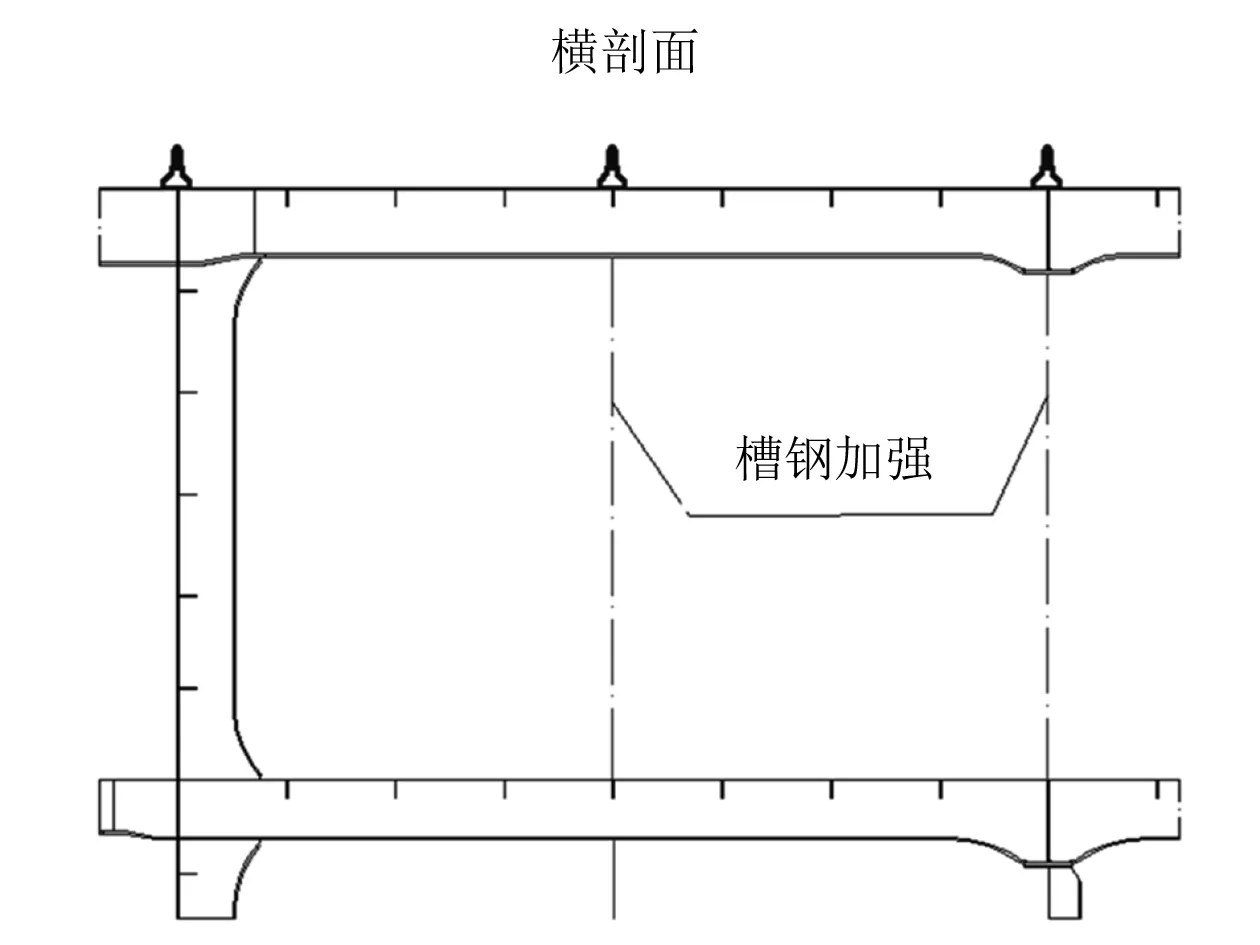
圖4 吊碼反面槽鋼加強

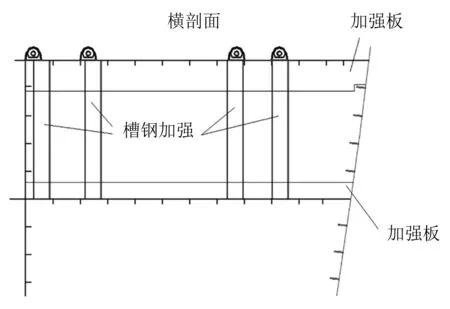
圖5 吊碼反面加強板加強

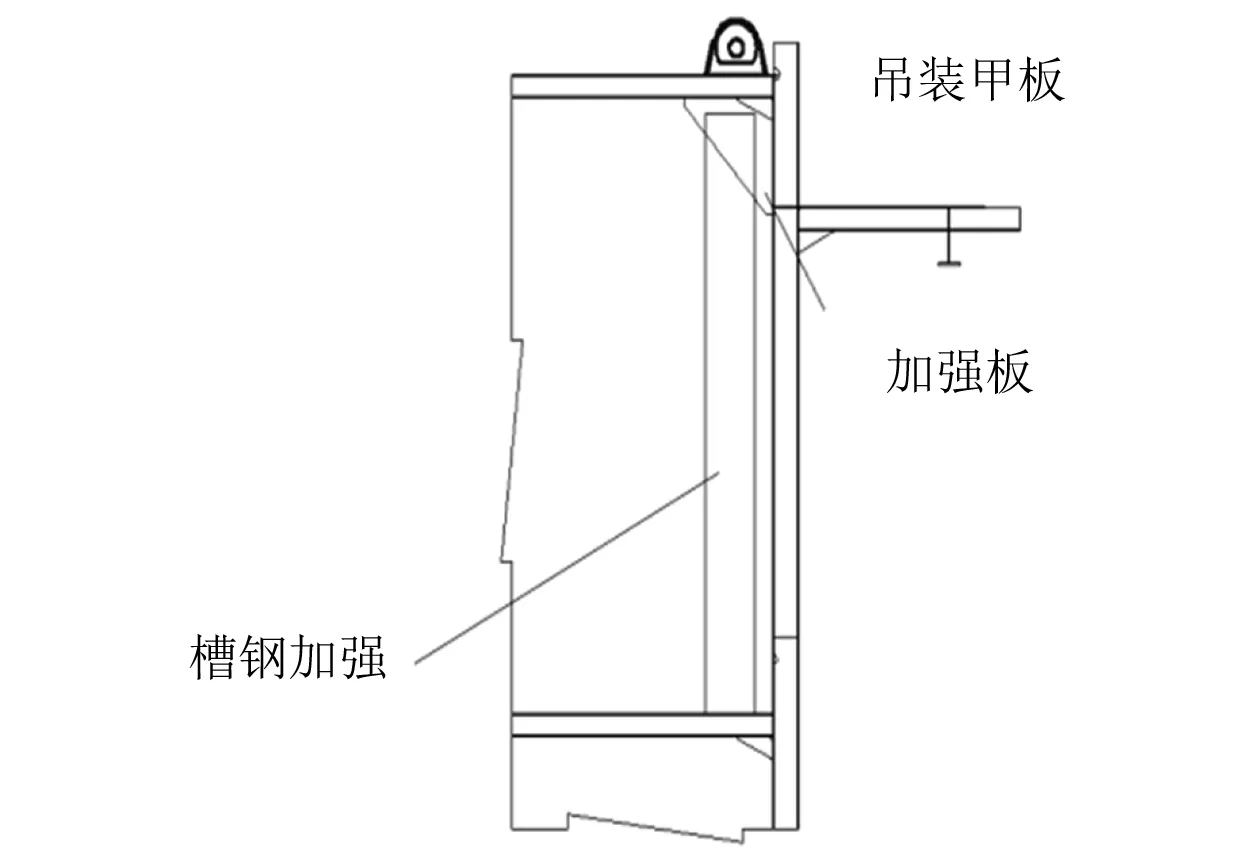
圖6 吊碼反面角隅加強

3 起升因數選取

在總段吊裝過程中外載荷僅施加重力場載荷，重力加速度g=9.80 m/s2。

在吊運過程中，由于加速度和沖擊的影響增加起升動載力，需要在計算過程中增加起升因數φh。根據相關文獻[3]及規范[4]，起升因數按如下公式計算：

φh=1+CV

(1)

式中：φh為起升因數；C為起重機剛度因數，臂架式起重機取0.30，門式起重機取0.60；V為起升速度，m/s，在起升速度超過1.0 m/s時，仍按1.0 m/s計算。

在任何情況下臂架式起重機的φh應不小于1.10，門式起重機的φh應不小于1.15。計算載荷為總段自重乘以起升因數φh。

根據公司搭載部門反饋，根據吊裝質量，1 600 t門式起重機吊裝速度分別為：空吊，6.0 m/min；500 t，5.0 m/min；800 t及以上，3.0 m/min。

在計算中，吊裝速度取極端速度6.0 m/min，即V=0.1 m/s，C=0.60。根據公式計算，φh=1.06，但根據規范φh應不小于1.15。同時考慮吊裝過程中的環境影響及不確定因素，計算取起升因數為1.20，則實際施加載荷的重力加速度g=11.76 m/s2。

4 滑輪等效模擬

在實際吊裝中，吊排采用多級滑輪結構以平衡各鋼絲繩的受力。但在有限元建模中若僅用桿單元模擬鋼絲繩，不考慮滑輪結構，則總段質量分布的不均勻性將導致各鋼絲繩受力不等，與實際情況不符，因此需要對滑輪結構進行等效模擬。

對于單個滑輪，由于其左右兩側鋼絲繩拉力的力臂相等，均為滑輪半徑，因此在平衡狀態下拉力相等。基于該原理，構建等腰三角形平衡桿[5]，如圖7所示，其中：R為滑輪半徑；F1和F2為滑輪鋼絲繩所受外力。平衡桿采用桿單元建模。為防止平衡桿變形對結果產生較大影響，平衡桿截面積或彈性因數應高于鋼絲繩1個量級。

圖7 單滑輪等效模型

以平衡桿頂點作為支點，支點約束3個方向的平動自由度；兩側鋼絲繩拉在平衡桿2個底點，底點約束垂直紙面方向的平動自由度。使平衡桿僅在面內繞頂點轉動。保證兩側鋼絲繩與平衡桿底邊夾角相等，即可確保兩側鋼絲繩拉力相等。

對于多級滑輪結構，采用多級等腰三角形平衡桿組合等效模擬，如圖8所示，其中：R1～R3為各級滑輪半徑，F1～F6為滑輪鋼絲繩所受外力。以Ⅰ級平衡桿頂點作為支點，支點約束3個方向的平動自由度；以Ⅰ級平衡桿底點作為Ⅱ級平衡桿頂點，Ⅱ級平衡桿各點均約束垂三角面方向的平動自由度[6]，如圖9所示。

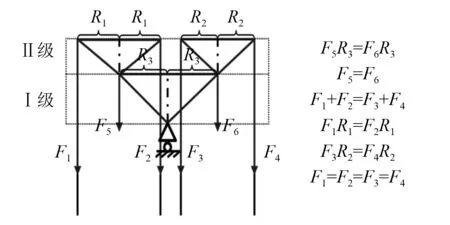
圖8 多級滑輪等效模型

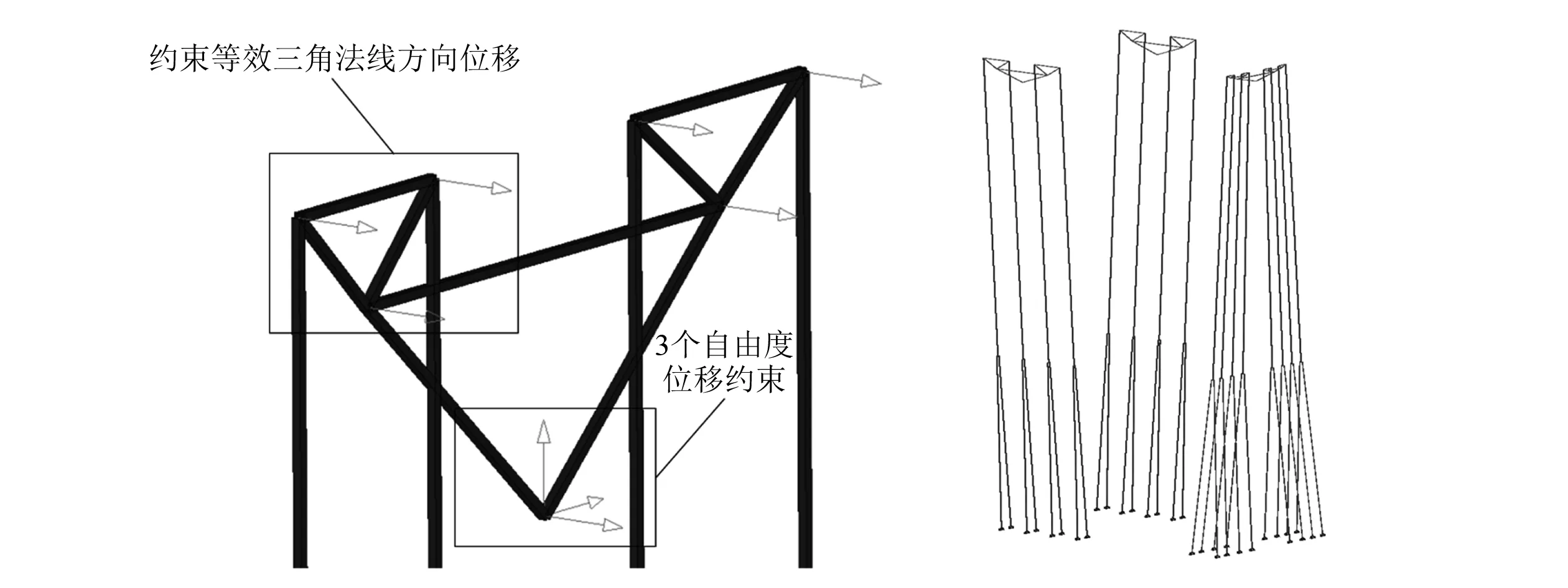
圖9 多級滑輪有限元模型

5 總段吊裝仿真初步計算

根據上述輸入條件，建立吊裝系統完整有限元模型，提交計算，得到相應結果，對甲板吊碼附近及槽鋼端部附近結構應力及整體變形進行分析。總段有限元模型中的吊裝系統及總段吊裝甲板如圖10所示。

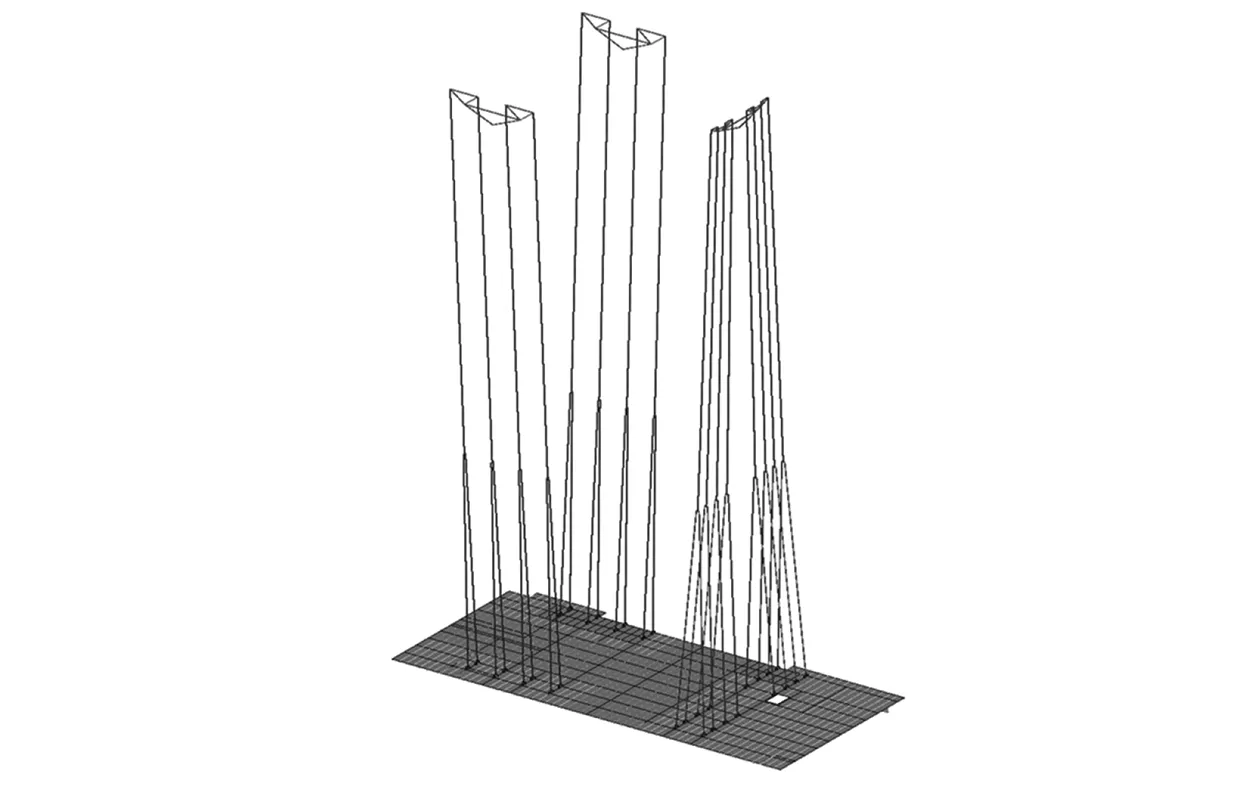
圖10 吊裝系統及吊裝甲板示例

在有限元模型分析過程中應注意如下各點：(1)吊碼附近結構為考察區域，需要對該區域網格進行細化，根據船級社及相關設計準則，將網格細化為50.0 mm×50.0 mm，如圖11所示；(2)吊碼附近采用一維單元建立的型材，需要將其轉換為二維板單元，其應力反映更加真實，如圖12所示；(3)計算完成，有限元軟件中的Displacement模塊顯示總段整體位移值，包括鋼絲繩變形，因此考察吊裝甲板區域變形需要對甲板進行單獨考察。

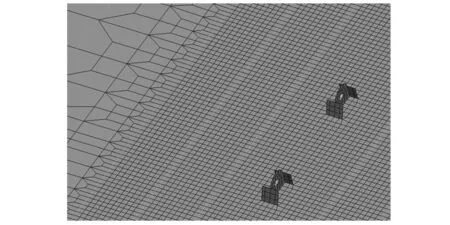
圖11 網格細化

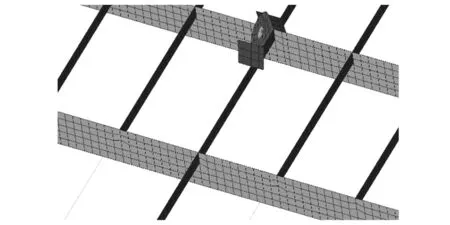
圖12 板單元型材

5.1 變形情況

計算結束，為考察吊裝甲板變形情況，需要將甲板提取出來進行單獨分析。吊裝甲板艏部與主橫艙角接，由于甲板與橫艙壁角接一條線上的甲板變形微小，因此可以該線為基準線，認為其變形為0，通過其他區域與基準線的位移值之差得到其他區域的變形值。

吊裝甲板變形趨勢如圖13所示。通過與基準線位移值之差，得到相應位置的變形值，正數為凸起，負數為下凹。由圖13可知：吊碼附近的變形較小，最大變形值為自由邊的18.0 mm，該變形主要是由吊碼受力后產生的彎矩所致，對整體結構影響不大。

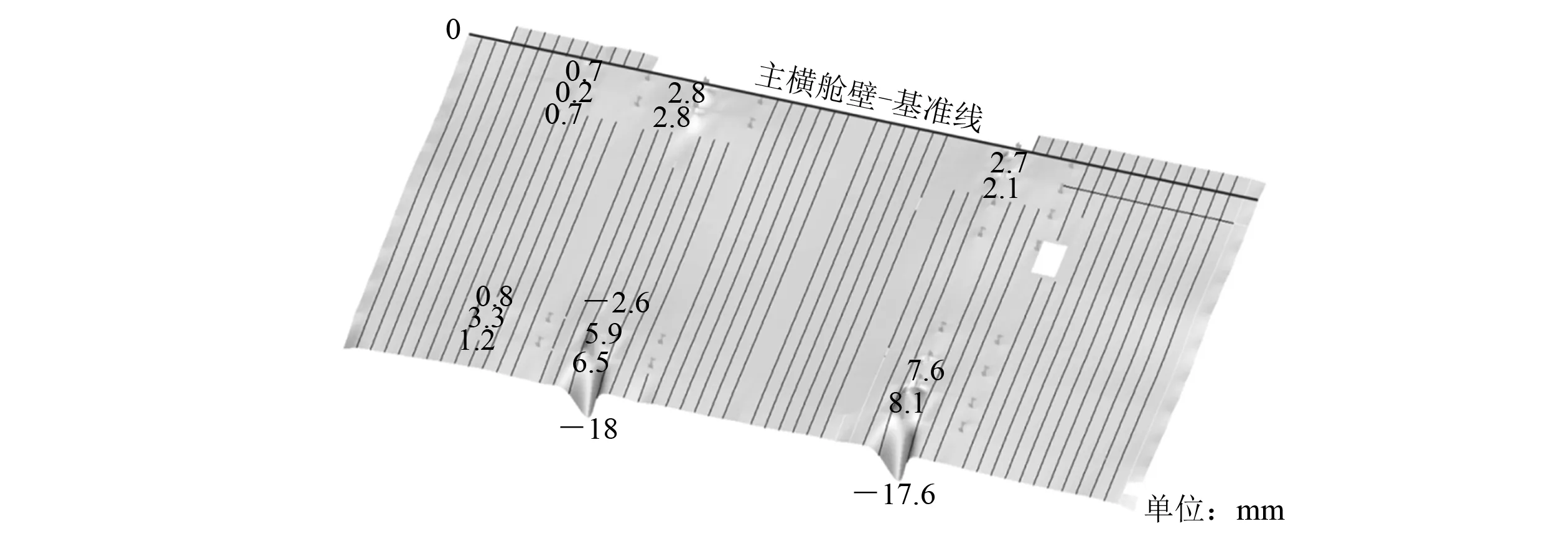
圖13 吊裝甲板變形趨勢示例

5.2 吊碼受力情況

根據門式起重機起吊原理及定滑輪原理，在同一吊排上，各吊碼受力的受力應當均勻，因此對仿真結果中的吊碼受力情況進行分析。不同吊排下的吊碼受力情況如圖14和圖15所示。

圖14 1號吊排下的吊碼受力

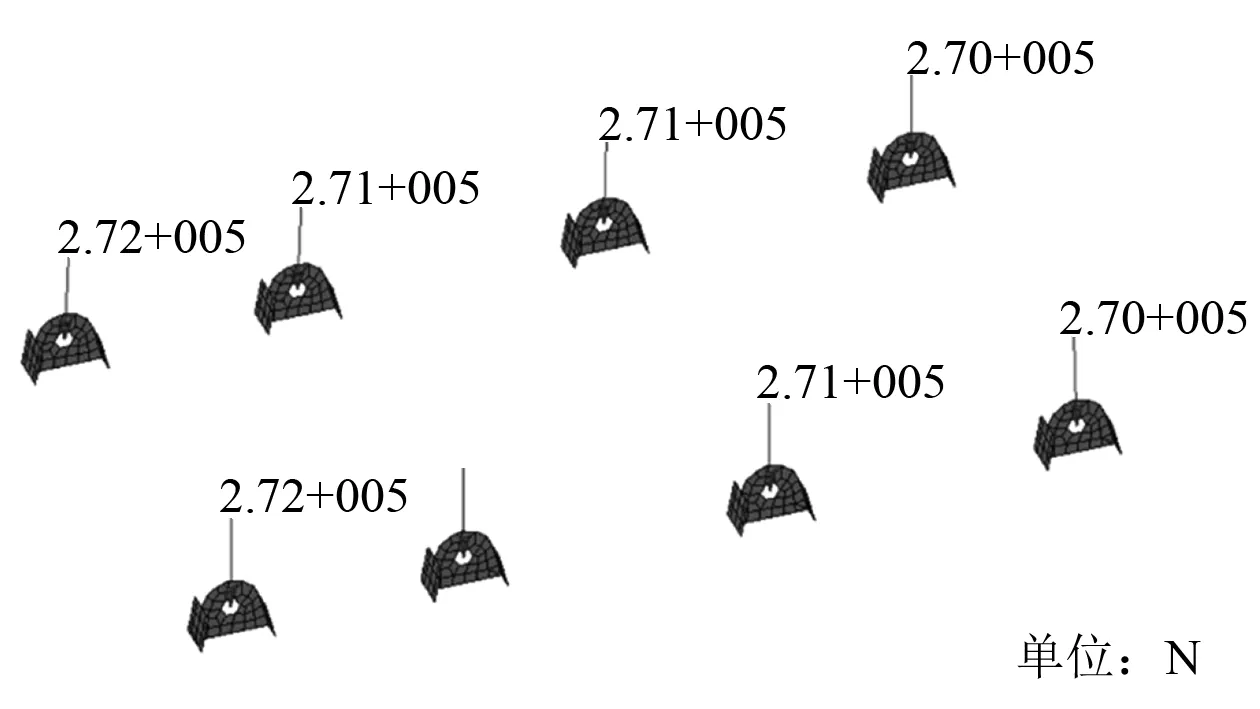
圖15 2號吊排下的吊碼受力

對不同吊排下的吊碼受力情況進行分析，同組吊碼受力基本一致，微小差別可能由軟件精度或三角等效系統偏差引起，但誤差可接受。值得注意的是：所有吊碼受力之和除以起升因數及重力加速度，其值應等于總段質量。

5.3 結構應力分布情況

通過數值仿真，得到總段吊裝的結構應力分布，總段結構所用材料許用應力為234 MPa，則以該值為基準，查找超過衡準的區域。應力超衡準部位如圖16所示，圖中陰影部位應力皆小于衡準，超過部分以云圖形式顯示。通過對比與分析，超衡準部位集中在吊碼下方縱向骨材處。縱向骨材規格偏弱，吊碼一端踩在橫向構件上，另一端僅踩在縱骨上，吊裝產生的彎矩會導致縱骨出現較大應力，因此考慮將結構較弱部分進行補強。

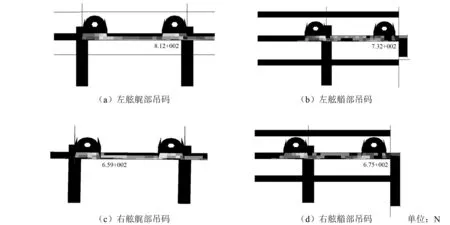
圖16 應力超衡準部位

6 總段吊裝仿真優化計算

分析總段吊裝仿真計算的整體狀態，吊裝甲板變形總體較好，各組吊碼受力均勻，局部區域出現結構應力超衡準情況，應對該部分進行有針對性的加強優化。通常的補強方式如下：(1)吊碼反面增加短筋，形成密集框架結構，如圖17所示；(2)縱骨腹板裝焊加強板，提高縱骨抗彎抗扭能力，如圖18所示；(3)局部區域增加槽鋼加強。

圖17 短筋加強

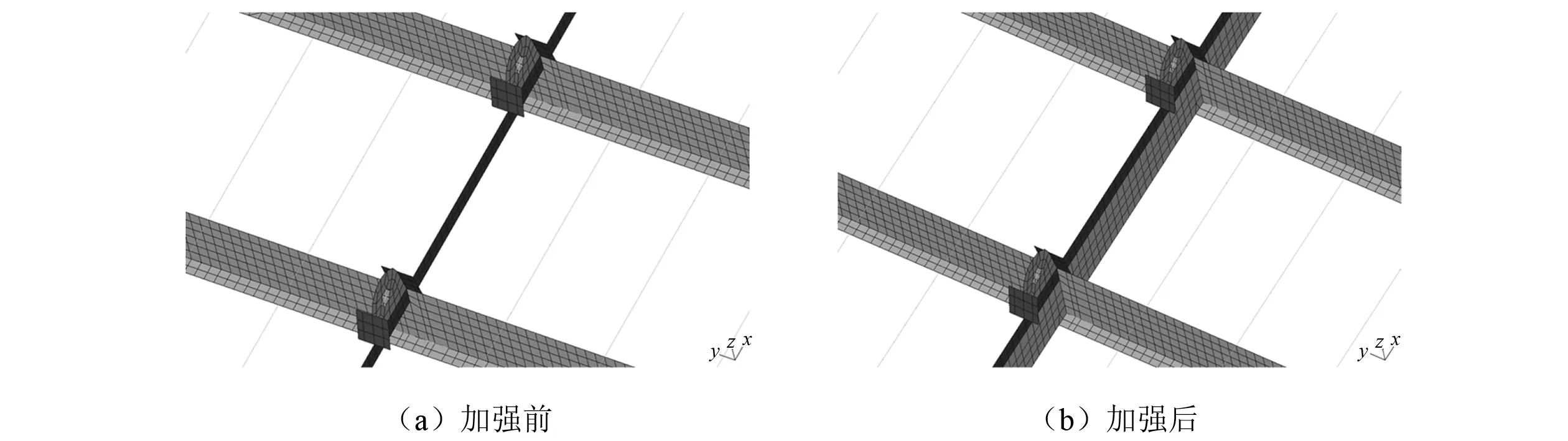
圖18 腹板加強

6.1 變形情況

通過結構補強和優化，對總段吊裝過程重新模擬仿真，其吊裝甲板變形情況如圖19所示。

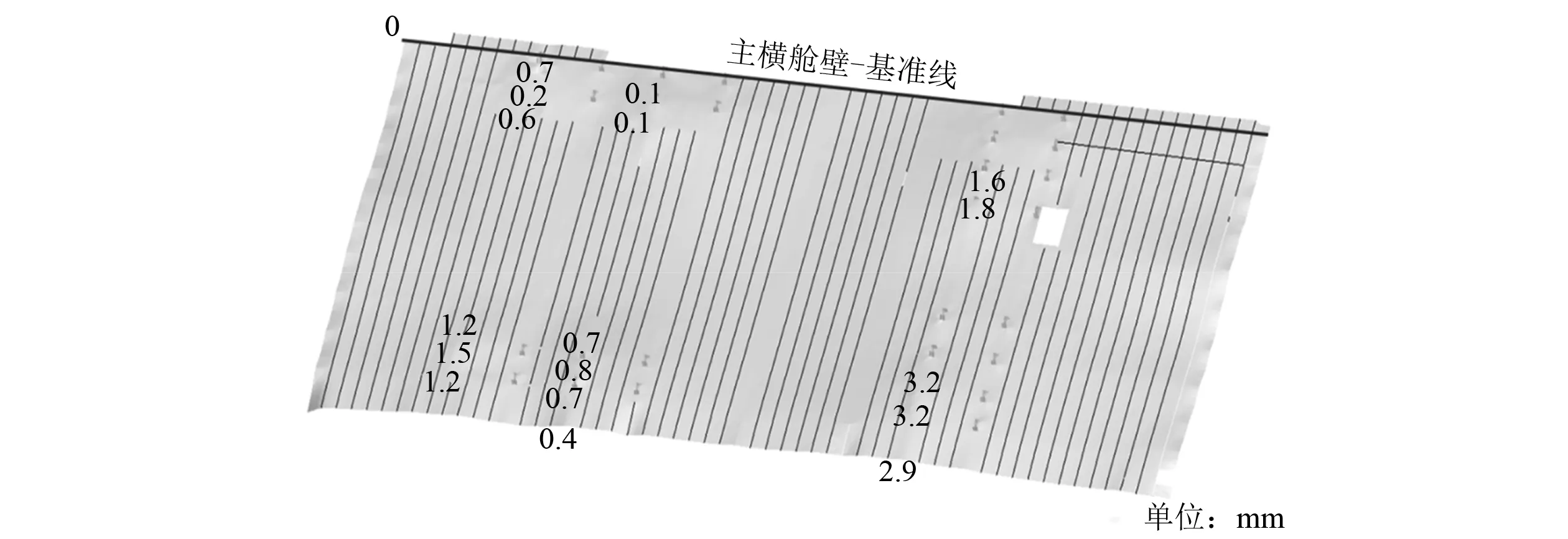
圖19 結構優化的吊裝甲板變形示例

經過有針對性的結構加強，甲板面變形情況得到緩解，自由邊由彎矩形成的大變形得到優化，說明加強結構可較好地分擔與傳遞吊碼受到的拉力及產生的應力。

6.2 結構應力分布情況

由于結構加強新增質量較小，對總段整體質量重心影響微小，對各組吊碼受力影響不大，因此不再考慮吊碼受力，直接分析相應部分的結構應力分布情況，對應力超衡準吊碼附近應力進行校核。結構優化的應力云圖如圖20所示。通過結構優化，超衡準區域應力大幅下降，最大值為200 MPa，在理論計算中結構可安全吊裝。

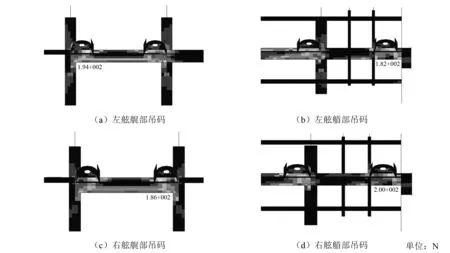
圖20 結構優化的應力云圖

7 結 語

利用仿真技術選定某工程大型薄甲板總段進行吊裝仿真和優化，可有效獲取總段吊裝過程中的應力分布及變形情況，較為準確地發現結構硬點，從而有針對性地對結構進行補強，對吊裝方案進行優化，保證總段吊裝順利、結構安全。在仿真過程中，對吊裝計算的方法、步驟、因數選取和吊排與吊碼的模擬及結果讀取方法進行詳細描述，可為類似結構的吊裝或其他靜態計算項目提供一定的方法和原理借鑒。