網格網不住學生的思維
——對金華網格作圖中考題的思考

徐琴輝

(浙江省東陽市吳寧第一初級中學 浙江 東陽 322100)

1.原題

(2018年第20題)如圖，在6×6的網格中，每個小正方形的邊長為1，點A在格點(小正方形的頂點)上．試在各網格中畫出頂點在格點上，面積為6，且符合相應條件的圖形。

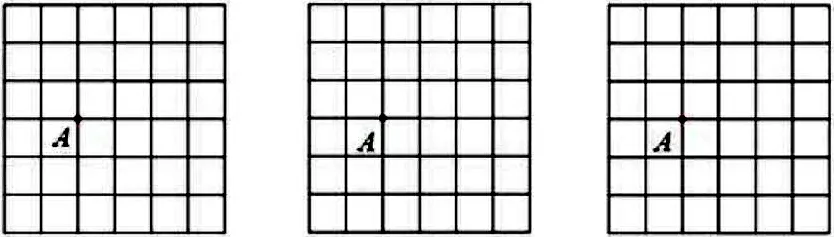
圖1:以點A為頂點的三角形 圖2:以點A為頂點的平行四邊形 圖3:以點A為對角線交點的平行四邊形

(2019年第20題)如圖，在7×6的方格中，△ABC的頂點均在格點上．試按要求畫出線段EF(E，F均為格點)，各畫出一條即可。

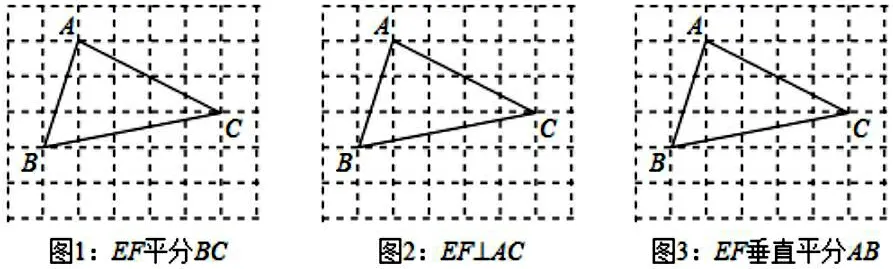
這兩題是經典的數學開放題。國家教委將“數學開放題”列為九五重點科研項目。我們數學教育不僅要讓學生學會必需的數學基本知識、基本方法、基本技能，更重要的是讓學生學會用數學的眼光看待世界，用數學的思維方式去觀察分析現實社會，去解決現實生活中的問題。數學開放題對培養學生思維的發散性、創造性不失為好的載體。

細看這兩題，每題都有3小題構成且有大前題，每小題又分別有不同的要求。我們可以發現編者的良苦用心:(1)條件開放,每小題的要求不同；(2)結論開放,每小題都有多種不同的畫法；(3)策略開放,每位學生的知識水平不同，產生思考的角度不同。這兩題都放在20題的位置,應該難度不大，但中考考試的情況是:學生到了這里就皺起了眉頭，原來解題的速度也慢下來了。在評卷過程中也發現了許多意想不到的失分點。這值得我們深思平時的數學教學。

2.近年來開放題教學的一些誤區

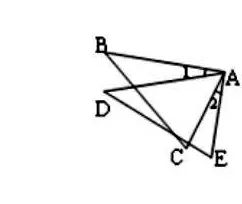
2.1 把開放題教成封閉題。比如，在三角形全等這章的教學中經常會出現如下的開放題:如圖所示，AB=AD，∠1=∠2，添加一個適當的條件，使△ABC≌△ADE，則需要添加的條件是________(只要寫出一種)。出題的意圖是讓學生用多種方法，多角度去思考這一問題，以便掌握三角形全等的各種方法。但有些教師為了學生不丟分，就讓學生填一對角相等的條件。而不去讓學生自由發揮，以便更好的了解學生，培養學生的發散思維。

2.2 缺乏對教材的挖掘，沒有進行很好的思維引導。

浙教版八下第五章5.1的作業題第4題:

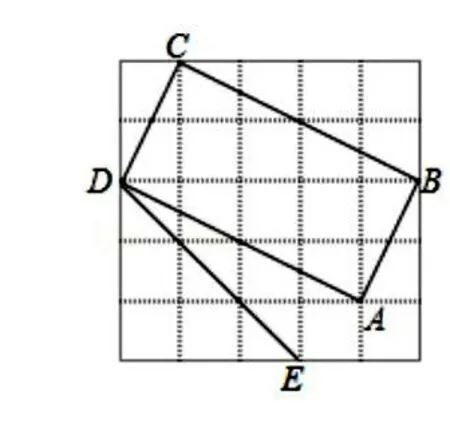
(1)判斷如圖5×5方格內四邊形ABCD是不是矩形，請說明理由。(2)以DE為一邊作一個矩形，要求另外兩個頂點也在方格頂點上。

其中的第2小題，許多教師可能只會讓學生去畫矩形，而沒有去引導學生畫的本質是畫直角，怎樣在網格中畫直角(或垂直)。

3.有效開展開放題教學，培養學生的深層數學思維方式

3.1 教師蹲下身子，多聽聽學生的思考情況。本人參加了2018年的中考數學改卷，詳細了解過20題的答題情況，真正體會到了“不看不知道，一看嚇一跳”的心境。在教學中我們教師再不能墨守成規了，學生比我們想象得厲害多。

以2018年的答題為例。

第1小題，面積為6的三角形：(1)底為4，高為3;(2)底為3，高為4;(3)底為6，高為2。

形狀:等腰三角形或直角三角形或一般三角形

第2小題，面積為6的平行四邊形(1)底為3，高為2 (2)底為2，高為3

形狀:平行四邊形→矩形；位置:邊在網格線上;邊不在網格線上

第3小題目，以A為對角線交點:底為3，高為2；底為2，高為3；以√2，3√2為邊的矩形。

在改這一題中，還發生的一點趣事。剛開始時，許多老師都認為這題是送分題，很好改，所以分到這組的老師較少。結果改了一天后，發現學生的答案五花八門，真是太多了，許多老師都看花了眼，以至改卷速度也相對是比較慢的一題。

3.2 課堂教學中教師要注重課堂生成、以學生為主體，讓學生插上想象的翅膀。從人學角度說，人是生成性的存在，人的發展具有豐富的可能性，是不確定的、不可限量的，也是不可算度的。學生不是配合教師上課的配角，而是具有主觀能動性的人。他們作為一種活生生的力量，帶著自己的知識、經驗、思考、靈感、興致參與課堂活動，并成為課堂教學不可分割的一部分，從而使課堂教學呈現出多樣性、豐富性和隨機性。從課程角度說，課程不只是“文本課程”，而更是“體驗課程”，這意味著，課程的內容和意義在本質上并不是對所有人都相同的，在特定的教育情境中，每一位教師和學生對給定的內容都有其自身的理解，對給定內容的意義都有其自身的解讀。從教學角度說，教學不是教師教學生學、教師傳授學生接受的過程，而是教與學交往、互動的過程，師生雙方相互交流、相互溝通、相互啟發、相互補充，在這個過程中教師與學生分享彼此的思考、經驗和知識，交流彼此的情感、體驗與觀念，豐富教學內容，求得新的發現，教學是一個發展的、增值的、生成的過程。

基于此，在數學開放題的課堂教學中，我們教師更應注重課堂生成，少些課堂預設。教師要轉變角色和教學行為，要不斷地捕捉、判斷、重組課堂教學中從學生那里涌現出來的各種信息，把有價值的新信息和新問題納入教學過程，使之成為教學的亮點，成為學生智慧的火種。教師只能引導學生自由、主動地生成和發展，讓學生真正成為課堂的主人，發散他們的思維，讓他們插上想象的翅膀。

葉瀾教授所指出的：“教師只要思想上真正顧及了學生多方面成長、顧及了生命活動的多面性和師生共同活動中多種組合和發展方式的可能，就能發現課堂教學具有生成性的特征。”如果說，傳統課堂把“生成”看成一種意外收獲，那么新課程則把“生成”當成一種價值追求；如果說傳統課堂把處理好預設外的情況看成一種“教育智慧”，新課程則把“生成”當成彰顯課堂生命活力的常態要求。可以說，生成是新課程課堂教學的一個亮點，它體現了課堂教學的豐富性、開放性、多變性和復雜性，激發了師生的創造性和智慧潛能，從而使課堂真正煥發出生命活力。

3.3 采用“一課一題”模式，開展開放題的復習課教學。

以2019年的為例，我設計了如下一節復習課。

設計的指導思想:教師的角色定位，即在教學過程中，教師不是教學活動的主角，而是“編劇”和“導演”；不是知識的傳授者，而是教學內容和教學活動的設計者、促進者、示范者、組織者、調控者。

引入:復習尺規作圖:平分一條線段，作已知線段的中垂線。

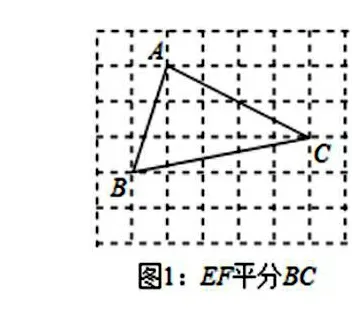
出示第一小題:在7×6的方格中，△ABC的頂點均在格點上．試按要求畫出線段EF(E，F均為格點).

問題引領：(1)平分線段想到什么?(2)進行不同的嘗試?

給學生充分的思考時間，教師選擇有代表性、典型性的幾位學生進行展示，并講解自己的思考切入點。

(總結:平分想到中點，平行四邊形的對角線互相平分)

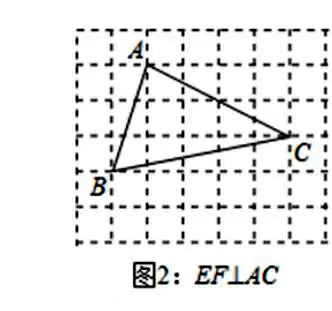
出示第二小題:在7×6的方格中，△ABC的頂點均在格點上．試按要求畫出線段EF(E，F均為格點)。

問題引領:(1)垂直想到什么?(2)進行不同的嘗試?

給學生充分的思考時間，教師選擇有代表性、典型性的幾位學生進行展示，并講解自己的思考切入點。

(總結:垂直想到直角，菱形和正方形的對角線互相垂直)

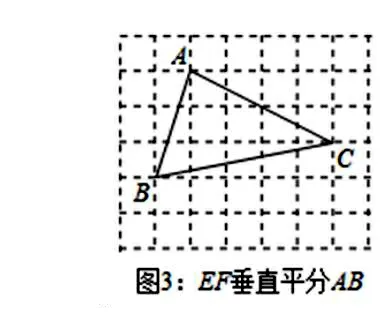
出示第三小題:在7×6的方格中，△ABC的頂點均在格點上．試按要求畫出線段EF(E，F均為格點)。

問題引領: (1)垂直平分想到什么? (3)怎樣的四邊形的對角線是互相垂直平分的?

(總結:菱形和正方形的對角線互相垂直平分)

給學生充分的思考時間，教師選擇有代表性、典型性的幾位學生進行展示，并講解自己的思考切入點。

最后，學生小結學習中的一些收獲和困惑；教師總結，數學培養的是我們的思維方式，碰到問題多思考，辦法總比問題多。

3.4 今后的教學啟示。

(1)注重幾何直觀，提升思維靈動。在中對學生要求經歷借助圖形思考問題的過程，初步建立幾何直觀。幾何直觀主要是指利用圖形和分析問題，借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。幾何直觀可以幫助學生直觀地理解數學，在整個數學學習過程中都發揮著重要作用。幾何直觀解題經驗的積累能提升學生思維靈動性，進而使學生的數學能力產生質的提升。

(2)注重思維變式，促成思維生長。思維變式能力的培養依賴于變式教學。數學變式教學是通過變更數學概念的非本質特征來暴露問題本質特征的教學方法。有效的變式教學需要在具體和特殊的，有序變化的情境中，用類比、歸納等方法認識相關問題的差異性和共性，從而抽象出數學問題的本質。思維變式的最終目的還是為了思維生長。變式最主要還是為了不變。

(3)注重學生生成，課前充分預設。課堂生成不是信馬由韁、漫無邊際，而是緊扣教學目標、圍繞教學內容、基于學生認識，通過教學活動促進學生知識掌握、思維發展、習慣養成、能力提升，所有這些都必須基于課前的充分預設。充分的預設要求教師在課前認真研究教材，分析學生認知結構，確定教學重點和難點。在教學實施中，當學生的活動偏離了預設時，教師不要打斷學生思維，而要通過設問把引導到預設的教學目標上來。在課堂中多進行開放式的教學有利于生成性資源的產生。真正的發現之旅不在于尋找新的景觀，而在于擁有新的眼界。

總之，在開放題的教學上要教師要注意講究“放”的策略，既要大膽地“放一放”，把時間留給學生，讓學生有機會去探索全面、正確的結論，又要善于把握全局，調控“放”度，凡是學生能提的問題，教師決不代替；學生能思考的問題，教師決不暗示；學生能解決的問題，教師決不插手，真正做到適時而“放”，提高“放”的整體效率。

希望我們教師在平時的教學中，多思考數學的本質是什么，什么是我們要教給學生的，什么是學生終身有用的。讓學生真正體會數學的魅力,愛上數學。