基于IPSO-MPC的無人駕駛車輛縱向運動控制

李廣南 葉洪濤 羅文廣

摘? 要：針對無人駕駛車輛縱向控制中的速度跟蹤精度問題，提出一種基于改進的粒子群優化算法（improved particle swarm optimization，IPSO）的模型預測控制方法。首先，在模型預測控制中將問題轉換為二次規劃問題，使用粒子群算法進行求解，并通過分層縱向控制器，實現對速度的跟蹤控制。為降低其陷入局部最優解的風險，引入了隨機權重策略和學習因子調整策略。其次，為了提高粒子尋優的速度，保存了上一時刻的最優粒子序列作為下一時刻粒子的群體極值。最后，為了驗證算法的有效性，通過Simulink/CarSim建立了聯合仿真平臺，仿真結果表明，該算法有效提高了車輛速度跟蹤的控制精度，最大誤差減小了0.274 7 km/h。

關鍵詞：無人駕駛車輛;模型預測控制;粒子群算法;縱向控制

中圖分類號：TP273;U471.15? ? ? ? ? ? DOI：10.16375/j.cnki.cn45-1395/t.2022.01.014

0? ? 引言

運動控制是無人駕駛車輛研究領域中的核心問題之一，車輛根據周圍環境以及車輛狀態信息向油門、剎車以及轉向系統等發出控制指令[1]。其中，縱向控制主要研究車輛的速度跟蹤能力，控制車輛按照預定的速度行走是實現車輛穩定跟蹤期望軌跡的關鍵。

模型預測控制（model predictive control，MPC）具有預測模型、滾動優化和反饋校正等特點，適用于不易建立精確數學模型且存在約束條件的控制。 文獻[2]提出了一種模型預測控制（MPC）框架的自動地面車輛速度跟蹤的控制方法，結合簡單的縱向逆動力學模型和MPC自適應調節，實現車輛縱向速度的控制。文獻[3]提出了一種分層控制架構下的智能電動汽車縱向跟車運動自適應模糊滑模控制方法，上位控制器由滑模控制器與自適應模糊控制器組成，下位控制器根據控制方式由縱向動力學逆模型計算出期望力矩，實現對加速度期望值的跟蹤。同樣地，文獻[4]使用車輛縱向運動的上下位分層控制器結構，在上位控制器中提出改進的MPC算法，下位控制器根據期望加速度求解發動機節氣門開度和制動壓力。

眾多研究學者還將其他優化算法加入縱向運動控制中。文獻[5]引入了一種帶有混沌初始化的粒子群優化算法（CPSO），將其應用到模型預測控制中， 用于解決同時帶有輸入約束和狀態約束的控制問題。文獻[6]設計了基于PSO算法的模型預測控制器，通過粒子（MPC中的參數[Np]、[Nc]）和該粒子所對應的適應值（控制系統的性能指標）建立聯系，能夠有效地對車輛軌跡進行跟蹤。文獻[7]通過數值驗證，證明使用一種改進的粒子群算法可以降低計算迭代次數，減少MPC計算成本。

縱向控制可分為直接式和分層式2種控制方式，為了便于研究控制系統，本文采用分層控制結構。在上位控制器中，針對二次規劃求解優化問題不夠精確的問題， 對基本粒子群算法進行改進，由此設計上位控制器輸出期望的加速度，下位控制器運用逆縱向動力學輸出期望節氣門開度和期望制動壓力，對車輛速度跟蹤效果問題進行研究。

1? ? 無人駕駛車輛縱向控制器策略

無人駕駛車輛的縱向速度控制器框圖如圖1所示。根據參考速度以及道路信息，縱向上位控制器對參考速度進行跟蹤控制，通過目標函數得到控制量，輸出車輛的期望加速度[ades]給下位控制器。下位控制器運用切換邏輯以及逆縱向動力學輸出期望節氣門開度信號[αthdes]或期望制動主缸壓力信號[Pbdes]，控制無人駕駛車輛跟蹤期望的速度。

2? ? 縱向控制器設計

2.1? ?上位控制器設計

車輛在行駛過程中，假設沒有橫擺運動對車輛縱向運動控制的影響，近似認為車輛的加速度等同于縱向速度的導數，利用一階慣性系統[8]來表示：

[a=（K/τd）×（ades-a）]，? ? ?   ? ? ? ? ? ? （1）

其中：[a]為縱向加速度，[ades]為期望加速度，[K]為系統增益，[τd]為時間常數。

考慮速度與加速度之間的關系，速度跟蹤控制用連續系統的狀態方程表示：

[x=Ax+Bu]，? ? ? ? ? ? ? ? ? ? ? ?（2）

式中：[x∈R2]為系統縱向狀態變量，[x=[va]T];[u∈R]為系統控制輸入，[R]為實數集， [u=ades];[A=010-1/τd]，[B=0K/τd]。將式（2）通過向前歐拉法進行離散化處理，得系統的離散狀態方程：

[x（k+1）=Akx（k）+xku（k）]，? ? ? ? ? ? ? （3）

其中，[Ak]、[xk]分別為狀態矩陣和控制輸入矩陣，矩陣分別表示為[Ak=1Ts01-Ts/τd]，[xk=0KTs/τd]，[k]為當前采樣時刻，[k+1]為下一采樣時刻，[Ts]為采樣周期。

系統輸出量為車輛速度[v（k）]：

[v（k）=Cx（k）]，? ? ? ? ? ? ? ? ? ? ? ? ?（4）

式中：[C=10].

在無人駕駛車輛控制系統中，車輛的控制目標是在保證車輛不發生過于劇烈的加速度和加速度變化率的前提下，保證速度跟蹤精度，因此，將性能評價函數定義為：

[J（x（k）， u（k-1）， △u（k））=]

[i=1NPVp（k+i|k）-Vref（k+i|k）2Q+]

[i=1Nc△u（k+i）2W] ，? ? ? ? ? ? ? ? ? ?（5）

式中：[k-1]為上一采樣時刻，[NP]為預測步長，[Nc]為控制步長，[Vp（k+i|k）]為控制輸出預測值，[Vref（k+i|k）]為控制輸出變量參考值，[（k+i|k）]和[△u（k+i）]分別表示根據[k]采樣時刻的狀態信息來預測第[k+i]時刻的信息和第[k+i]時刻的控制輸入增量，其中[i=1， 2， …， Np];[Q]為系統輸出量的權重系統矩陣，[W]為系統控制增量的權重系統矩陣。

在控制器跟蹤速度過程中，需要考慮添加主動約束，即控制過程中的加速度約束及其變化率約束，保證其約束在合理的范圍之內，其不等式表達如下：

[umin≤u（k+i）≤umax]，[i=1， 2， …， Nc-1]，? （6）

加速度變化率約束表達形式為：

[△umin≤△u（k+i）≤△umax]，[i=1， 2， …， Nc-1]， （7）

其中：[umin]和[umax]為縱向加速度閾值，[Δumin]和[Δumax]為縱向加速度變化量閾值，[u（k+i）]是[k+i]時刻的控制輸入。

系統在每個周期完成對優化問題的求解，得出每個周期一系列的最優解控制輸入增量[ΔU*]，并將第一個控制增量作為系統的實際輸出變化量，加入系統中。在新的時刻，系統根據系統狀態，重新預測下一時刻的一系列控制增量，不斷在線滾動優化，直到完成控制過程。

2.2? ? 二次優化問題的轉化

結合性能要求，優化問題可以轉化為標準的二次規劃（QP）問題進行求解，式（7）可以簡化成以下形式：

[minΔU12ΔUTHΔU+GTΔU]，? ? ? ? ? ? ? ? ? （8）

[s.t.? ? ? ? ? ? ?ΔUmin≤ΔU≤ΔUmax]，

[Umin≤AtΔU+Ut≤Umax]，

式中：[H∈R2×2]對稱正定，[G∈R2]，[ΔU=Δu（k），Δu（k+1）， …， Δu（k+Nc）T]，[Ut=1Nc][?][u（k-1）]，[1Nc] 為Nc行的單位列向量，[u（k-1）]為上一時刻實際控制量，[ΔUmin]和[ΔUmax]為控制時域內加速度變化量的最小值、最大值集合，[Umin]和[Umax]為控制時域內加速度的最小值、最大值集合，[At=100…0110…0111…0????111…1Nc×Nc].該優化問題可以通過MATLAB提供的QP求解器quadprog函數來實現：

[ΔU?=quadprog（H， G， Ak， Bk）]

2.3? ?下位控制器設計

下位控制器的作用是根據期望加速度對車輛進行準確控制，該控制會涉及到車輛制動和驅動模式的切換過程，以及將控制量轉換為執行器控制? ? ?輸入。

考慮空氣阻力、滾動阻力以及坡度阻力，將車輛阻力需求加速度方程[9]用式（9）表示：

[mathre=Fres=Froll+Faero+Fgrade]，? ? ? ? ? ?（9）

式中：[m]為車輛質量，[athre]為阻力需求加速度，[Fres]為阻力合力，[Froll]為滾動阻力，[Faero]為空氣阻力，[Fgrade]為坡度阻力。

坡度阻力為汽車重力沿坡道的分力，在CarSim中設置了坡度為[ia]的直線道路，其中[ia=tanα]，[α]為坡角。因此，考慮坡度較小時，重力加速度g取9.8 m/s2，坡度阻力[Fgrade]：

[Fgrade=m×g×ia]，? ? ? ? ? ? ? ? ? ? （10）

滾動阻力[Froll]為：

[Froll=m×g×cosα×Cr]，? ? ? ? ? ? ? ?（11）

式中：[Cr]為滾動阻力系數。

空氣阻力[Faero]為：

[Faero=12×ρa×Sa×CW×v2]，? ? ? ? ? ? ?（12）

式中：[CW]為空氣阻力系數;[ρa]為空氣密度，正常的干燥空氣可取[1.29] kg/m3;[Sa]為車輛迎風面積。假設車輛在行駛過程中，以上參數均不發生變化。

在設計邏輯切換的過程中，要保證制動和驅動模式不能同時起作用，也要根據現實情況，不能頻繁地切換制動和驅動模式。因此，根據期望加速度定義以下邏輯切換：

[αthdes=αthdes， ades≥-αthre0， ades<-αthre]，? ? ? ? ? ? ? ? ? ?（13）

[Pbdes=0， ades>-αthrePbdes， ades≤-αthre]，? ? ? ? ? ? ? ? ? ? ?（14）

式中：[αthdes]為期望節氣門開度，[Pbdes]為期望制動主缸壓力。

經過驅動模式或制動模式的邏輯切換時，當期望加速度大于等于阻力需求加速度時，切換為驅動模式。考慮車輛內部的旋轉構件換算質量、道路坡度阻力、空氣阻力以及滾動阻力，可以得到驅動模式下車輛的驅動力[FE]為：

[FE=δmades+Fgrade+Froll+Faero] ，? ? ? （15）

式中：[δ]為旋轉質量換算系數，通過經驗公式得到。

因此得發動機所需的輸出扭矩[10-11]為：

[Te=FErwigi0η] ，? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（16）

式中：[rw]為車輪有效半徑，[ig]為變速器減速比，[i0]為主減速器傳動比，[η]為傳動系機械效率。根據車輛發動機轉速[n]、節氣門開度、發動機輸出扭矩[Te]三者的關系，以及轉速和有效扭矩，通過發動機扭矩[TMAP]可得到節氣門開度[αthdes]為：

[αthdes=T-1MAP（n， Te）]，? ? ? ? ? ? ? ? ? ? ? ?（17）

當邏輯切換為制動模式[12]時，考慮道路坡度阻力、空氣阻力以及滾動阻力，當前車輛需求制動力[FB]為：

[FB=-mades-Fgrade-Froll-Faero]，? ? ? ? ? （18）

期望的制動主缸壓力計算為：

[Pbdes=FBkB]，? ? ? ? ? ? ? ? ? ? ? ? ?（19）

式中：[kB]為制動力與制動主缸壓力的比值。

通過制動驅動模式切換以及計算，得到期望節氣門開度[αthdes]和期望制動主缸壓力[Pbdes]，將控制量作為執行器控制輸入，控制車輛根據期望的速度 行駛。

3? ? 優化PSO結合的MPC算法

采用模型預測控制進行速度跟蹤的基本思想是車輛在根據期望速度行駛的過程中，將最優化問題轉化為一個帶約束的二次規劃問題進行求解。針對原本QP算法在求解過程中出現精度不足的問題，本文利用改進型的粒子群優化算法對性能指標進行優化，解出控制律。

3.1? ?算法介紹

在粒子群算法中，假設在一個[S]維的目標搜索空間中，有[M]個粒子組成一個粒子群體，粒子在[S]維的搜索空間中以一定的飛翔速度搜索，每一個粒子所在的位置都是一個潛在的解，粒子根據目標函數計算出其適應值，根據適應值的大小判斷該粒子的優劣性。在[S]維中，第[i]個粒子的位置為：[Xi=xi1， xi2， …， xiS];第[i]個粒子的速度表示為：[Vi=vi1， vi2， …， viS]，[1≤i≤S]。粒子在游歷過程中，第[i]個粒子經歷過的歷史最好點，即個體極值[pbest]表示為：[PiS=pi1， pi2， …， piS];整個粒子群迄今為止搜索到的最好的位置，即群體極值[gbest]表示為? ? ? [PgS=pg1， pg2， …， pgS]，[g∈1， 2， …， M]。

空間中各粒子隨著每一次的迭代都會不斷地更新自己的狀態[13]，其速度和位置的更新方程為：

[viS（t+1）=ωviS（t）+c1r1（t）piS（t）-xiS（t）+c2r2（t）pgS（t）-xiS（t）]，? ? ? ? ? （20）

[xiS（t+1）=xiS（t）+viS（t+1）]，? ? ? ? ? （21）

式中：[ω]為慣性因子，其大小可以保證粒子的搜索能力，[ω]較大時可以保證全局的搜索能力，反之，局部搜索能力較強;正常數[c1]和[c2]稱為學習因子，分別調整粒子飛向自身、全局最好位置方向的步長;[r1]和[r2]為互相獨立且均勻分布于[0，1]的2個隨 機數。

設[f（x）]為最小化的目標函數，則第[i]個粒子當前位置[pi（t+1）]由以下公式確認：

[xiS（t+1）=xiS（t）+viS（t+1）]，? ? ? ? ? ? ?（22）

[pi（t+1）=pi（t）， f（xi（t+1）≥f（pi（t））xi（t+1）， f（xi（t+1）<f（pi（t））]. （23）

3.2? ? 改進粒子群算法

由于PSO在優化過程中會向自身歷史最佳位置以及群體中歷史最佳位置靠近，而且其優化速度跟其初始化設置參數有很大聯系，使得粒子容易陷入局部最優或停滯，導致輸出結果波動較大[14-15]。因此，為了提高粒子群算法效率，對粒子群算法進行改進。

3.2.1? ? ?添加壓縮因子

在優化過程中，算法容易陷入局部尋優中，會直接影響算法的性能，從而導致優化出的參數不精確。為確保算法的收斂性，在粒子的每一步移動過程中添加壓縮因子，不僅能夠滿足收斂速度，而且收斂精度大大提高。對粒子更新方程進行如下改進：

[viS（t+1）=ψωviS（t）+c1r1（t）piS（t）-xiS（t）+]

[c2r2（t）pgS（t）-xiS（t）] ，? ? ? ? ? （24）

[xiS（t+1）=xiS（t）+viS（t+1）] ，? ? ? ? （25）

式中：[ψ]為壓縮因子， [ψ=22-φ-φ2-4φ]，其中[φ=c1+c2>4]。

3.2.2? ? 調整慣性權重

在MPC計算求解過程中要求時間越短越好，在粒子群算法中需要多次迭代收斂才能尋找到最小值。慣性權重[ω]是PSO優化算法的可調參數之一，其大小控制了迭代過程中歷史因素對當前狀態的影響程度[16]。為了更好地平衡算法的全局搜索與局部搜索能力，加入了隨機權重策略[ω]，使得粒子的歷史速度對這一時刻速度具有隨機影響性，克服[ω]的線性遞減所帶來的不足。[ω]的取值為：

[ω=μ+σ×N（0， 1）μ=μmin+（μmax-μmin）×rand（0， 1）]，? ? ? （26）

式中：[μmin]為隨機權重平均值的最小值，[μmax]為隨機權重平均值的最大值，[σ]為隨機權重的方差，[N（0， 1）]表示標準正態分布的隨機數，[rand（0， 1）]表示[0]～[1]的隨機數。

3.2.3? ? ?調整學習因子

在基本的粒子群算法中，認為粒子在尋找最優值的過程中，其自我學習能力及群體的學習能力是一樣的，即學習因子[c1]、[c2]的取值是固定的;但是在迭代初級階段，粒子具有較強的自我學習能力，而在迭代后期，粒子需要較強的社會學習能力去快速收斂，尋找最優值[17-18]。因此，學習因子[c1]在算法求解過程中應呈線性遞增形式，學習因子[c2]在算法求解過程中呈線性遞減形式。

[c1=c1min+（c1max-c1min）×itKt]，? ? ? ? ? ? ?（27）

[c2=c2min+（c2max-c2min）×itKt]，? ? ? ? ? ? （28）

式中，[it]為當前迭代次數，[Kt]為最大迭代次數[（it=1， 2， …， Kt）]。但是在求解適應度函數值時，其收斂曲線并不是呈線性遞減的直線而是呈指數函數趨勢遞減的形式，這會導致學習因子的遞增遞減程度與適應度函數變化程度不一致的現象。因此，將線性遞增遞減的曲線修改為呈指數函數趨勢的曲線，與適應度函數變化曲線相匹配，設置學習因子形式如下所示：

[c1=c1min+（c1max-c1min）×（itKt）1it]，? ? ? ? （29）

[c2=c2min+（c2max-c2min）×（itKt）1it].? ? ? ? （30）

3.3? ? IPSO-MPC算法流程與步驟

經改進后的粒子群優化算法，其算法流程如 圖2所示[19]。

將粒子群算法和MPC相結合，把輸入向量[ΔU]作為優化變量，則粒子群中各個粒子的維數等同于預測的控制時域;目標函數選取式（8）計算各個粒子的適應度;由于這一時刻的優化變量的最優解與上一時刻優化變量的最優解的變化不大，為保證優秀粒子的影響力，將上一時刻的控制序列作為下一時刻粒子的[gbest]初值，提高算法的效率。算法的具體步驟如下：

Step 1? ?初始化[MPC]參數以及粒子群參數，采集第[k]時刻[Carsim]輸出的系統狀態量信息;

Step 2? ?根據車輛模型、狀態量和輸入量，計算出優化問題中的矩陣[H]和[G]，以及目標函數[J（△u（k））];

Step 3? ?運用粒子群優化算法進行求解，根據目標函數以及約束，進行迭代計算，直到滿足終止條件，得到該控制時域內的一系列控制輸入增量[ΔU];

Step 4? ?將該控制序列中第一個元素[△u?（k）]作為實際的控制輸入增量作用于系統中;

Step 5? ?令[k=k+1]，循環執行，直到系統完成控制過程。

4? ? 仿真驗證

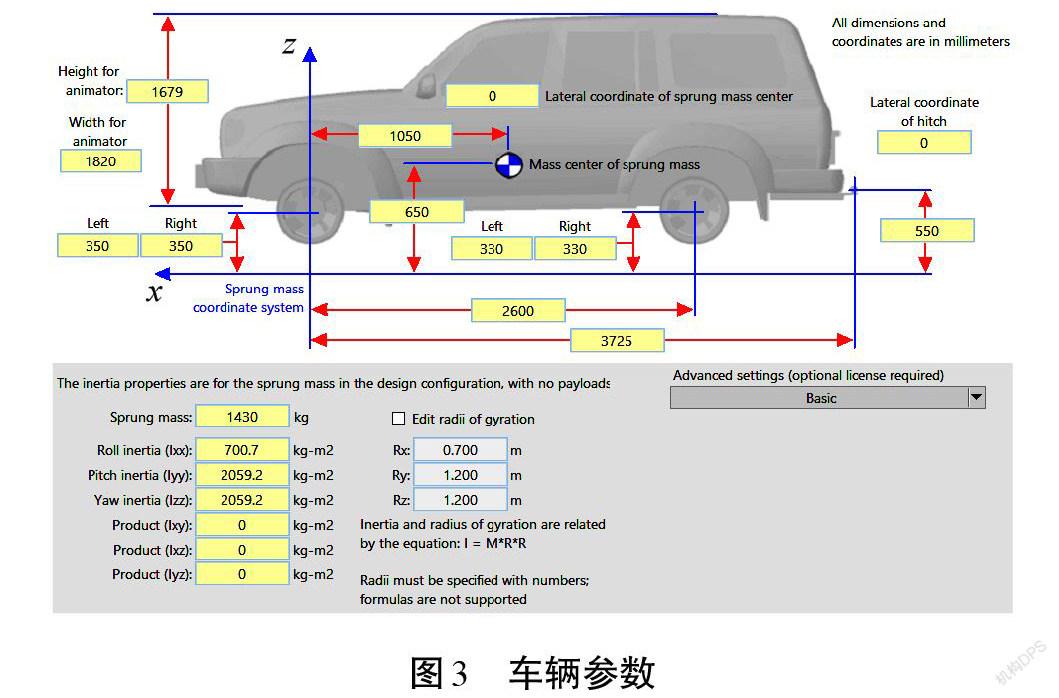
為驗證粒子群算法結合MPC算法的有效性，通過搭建Simulink/CarSim聯合仿真平臺，對所設計的控制器進行仿真驗證，并與MATLAB提供的QP算法進行比較分析。 在MPC控制器中，預測步長[Np=30]，控制步長[Nc=2]，采樣時間[Ts=0.02] s，[umin=-5] [m/s2]，[umax=3.5] [m/s2]，[Δumin=-5] [m/s2] ，[Δumax=5] [m/s2]，系統輸出量的權重系統系數[Q=200]，控制增量的權重系統矩陣[W=2]。粒子群算法中的參數數值為：最大迭代次數[Kt=100]，粒子群數目[M=30]，學習因子[c1=2.1]，[c2=2]，? [φ=4.1]，[μmin=0.5]， [μmax=0.8]，[σ=0.2]，壓縮因子[ψ=0.729 8]，[c1min=c2min=0.5]，[c1max=c2max=3.5]。由于不同的路面附著系數對車輛的控制量輸出有較大的影響，因此，將附著系數設置為0.85，并考慮車輛行駛坡道情況，設置在坡度[ia=0.05]的工況下進行測試。實際測試中，車輛空氣阻力系數數值為0.28～0.40。車輛迎風面積數值為1.4～2.6 [m2]，良好路面的滾動阻力系數為0.008～0.030。綜合考慮，模型參數取值為：滾動阻力系數[Cr=0.016]，空氣阻力系數[CW=0.280]，車輛迎風面積[Sa=2.51] [m2]，[rW=0.379] m，[i0=4.1]，[η=0.95]，[kB=]1 350 [N·m/Pa]。仿真測試選用的車型為D-Class，SUV，車輛具體參數如圖3所示。

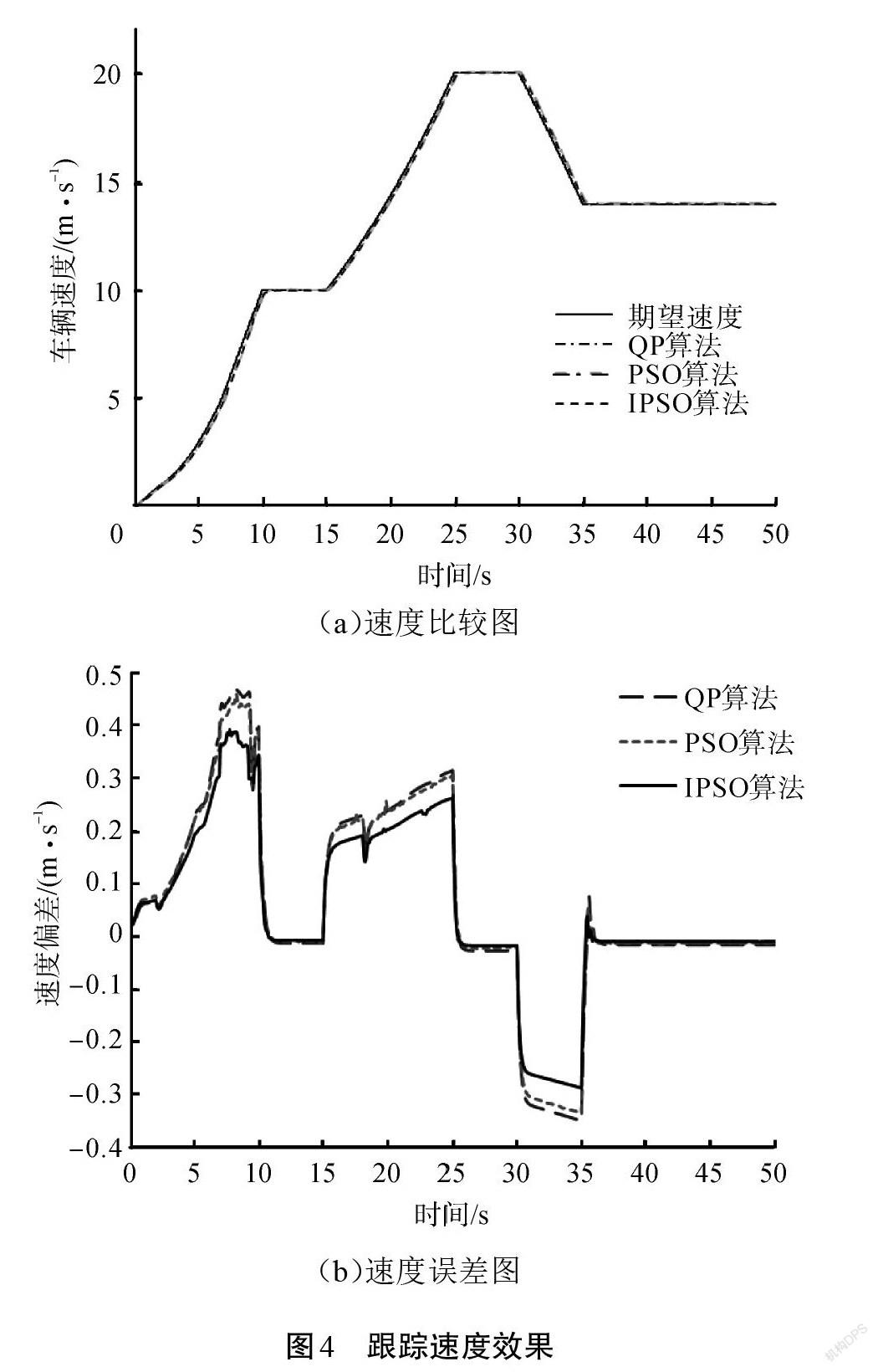
在有坡度的道路工況下，驗證控制器的有效性，設置了包含不同加速度的加速過程與減速過程的期望速度曲線，車輛根據該期望速度曲線進行速度跟隨控制，對控制算法進行仿真驗證，其車輛速度比較以及速度誤差圖如圖4所示。

如圖4所示，車輛的實際行駛速度與參考車速基本上重合，3種算法都能實現很好的跟蹤，在加速以及減速過程中會有較小的超調量，但隨后很快跟隨期望速度進行行駛。但在3種算法中，IPSO算法的誤差要比PSO和QP算法小，在加速過程中最大的跟隨誤差為0.392 2 m/s，減速過程的最大跟隨誤差為0.283 8 m/s，且整體的跟蹤誤差結果效果更好。控制器速度跟蹤誤差如表1所示。

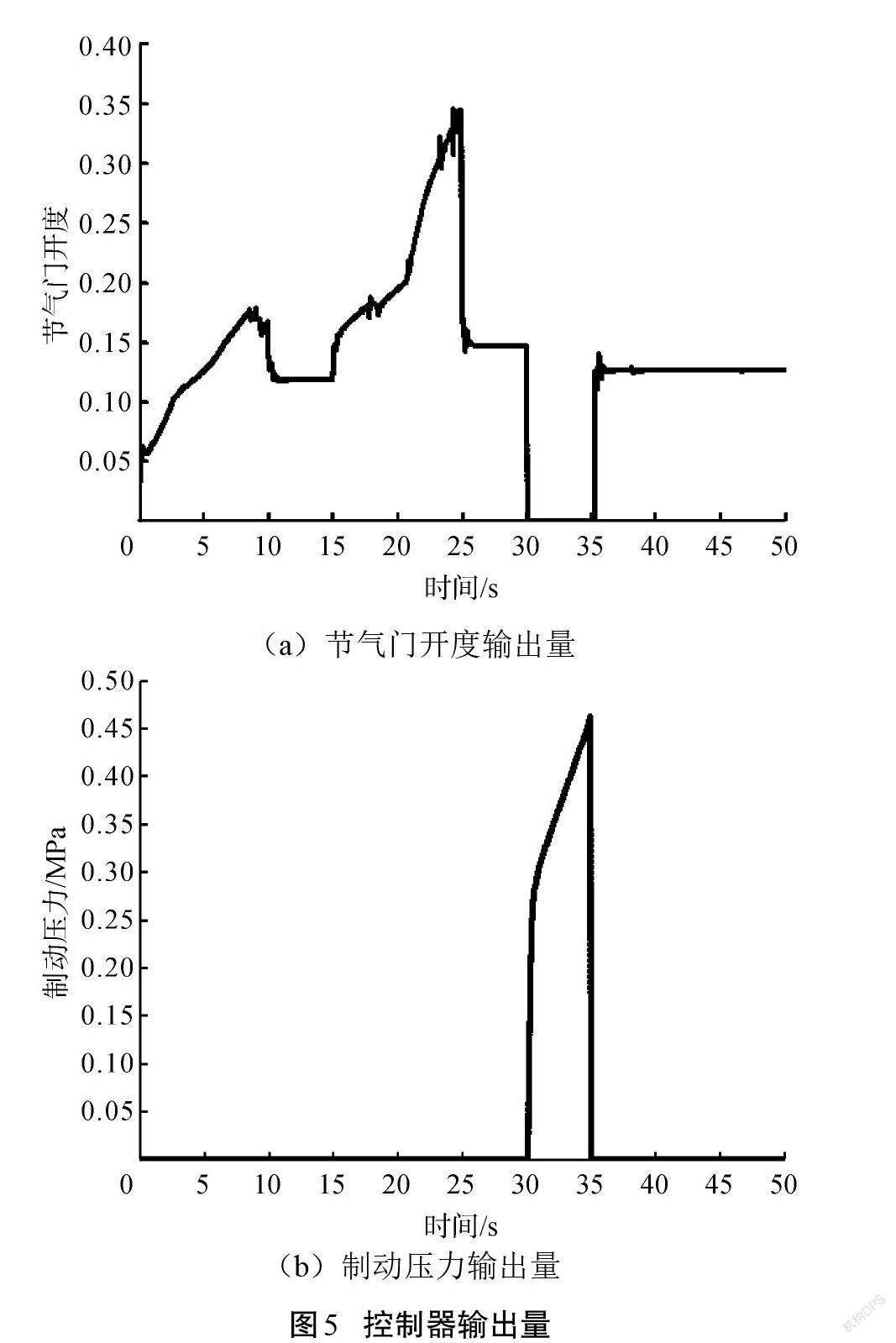
在IPSO控制器算法中，節氣門開度和制動壓力控制量如圖5所示，并沒有出現頻繁切換驅動制動模式及同時起作用的情況，滿足控制的需求。

同時，為控制系統的實時性，記錄單次解算時間，從控制器獲取車輛狀態信息進行問題的構建和分析求解，得到輸出控制量之間的時間長度。

對有坡度的道路工況中每個控制周期的單次解算所需時間進行統計，如圖6所示，加了IPSO優化算法的MPC控制器的計算時間約20 ms。由于IPSO算法是基于MPC框架，需要進行優化求解，單次解算時間相對于QP時間要長，但遠小于無人駕駛車輛實時控制周期50 ms，故滿足實時性要求。

5? ? 結論

本文針對基于模型預測控制方法的無人駕駛車輛縱向控制中的速度跟蹤精度問題，利用一種改進型的粒子群優化算法求解該問題。縱向速度控制采用分層控制結構，上位控制器采用一階慣性環節預測車輛狀態信息，利用IPSO優化算法求解目標函數的最優解，得出車輛的期望加速度;下位控制器通過逆縱向動力學模型得出期望節氣門開度以及制動主缸壓力，在Simulink/CarSim建立了聯合仿真平臺進行驗證，在有坡度的道路工況下能夠有效地使車輛實現縱向加速、勻速和減速的速度跟隨，并且控制車輛速度的最大誤差減小了0.274 7 km/h，符合控制實時性的要求，證明了改進型控制器的有效性。

參考文獻

[1]? ? ?郭景華，李克強，羅禹貢.智能車輛運動控制研究綜述[J].汽車安全與節能學報，2016，7（2）：151-159.

[2]? ? ?ZHU M，CHEN H Y，XIONG G M.A model predictive speed tracking control approach for autonomous ground vehicles[J].Mechanical Systems and Signal Processing，2017，87：138-152.

[3]? ? ?李文昌，郭景華，王進.分層架構下智能電動汽車縱向運動自適應模糊滑模控制[J].廈門大學學報（自然科學版），2019，58（3）：422-428.

[4]? ? ?劉富春，賀云，陳奕峰.時延MPC自主車輛協同控制算法與仿真[J].計算機工程與應用，2019，55（23）：222-227.

[5]? ? ?董娜，陳增強，孫青林，等.基于粒子群優化的有約束模型預測控制器[J].控制理論與應用，2009，26（9）：965-969.

[6]? ? ?唐傳茵，趙懿峰，趙亞峰，等.智能車輛軌跡跟蹤控制方法研究[J].東北大學學報（自然科學版），2020，41（9）：1297-1303.

[7]? ? ?周晶晶，徐友春，張自立，等.IPSO-MPC算法在智能車縱向速度控制中的應用[J].軍事交通學院學報，2017，19（4）：38-42.

[8]? ? ?龔建偉，姜巖，徐威.無人駕駛車輛模型預測控制[M].北京：北京理工大學出版社，2014.

[9]? ? ?謝輝，劉爽爽.基于模型預測控制的無人駕駛汽車橫縱向運動控制[J].汽車安全與節能學報，2019，10（3）：326-333.

[10]? ?李芳.智能車輛軌跡跟蹤的橫縱向協同控制研究[D].重慶：重慶郵電大學，2018.

[11]? ?HU P，GUO J，LI L H.A robust longitudinal sliding–mode controller design for autonomous ground vehicle based on fuzzy logic[J].International Journal of Vehicle Autonomous Systems，2013，11（4）：368-383.

[12]? ?鄧濤，李鑫.智能車輛橫縱向運動綜合控制方法研究[J].重慶交通大學學報（自然科學版），2021，40（4）：133-140.

[13]? ?MOHANTY P K，DEWANG H S. A smart path planner for wheeled mobile robots using adaptive particle swarm optimization[J].Journal of the Brazilian Society of Mechanical Sciences and Engineering，2021，43（2）：101-118.

[14]? ?高飛.MATLAB智能算法超級學習手冊[M].北京：人民郵電出版社，2014.

[15]? ?郁磊.MATLAB智能算法30個案例分析[M].北京：北京航空航天大學出版社，2011.

[16]? ?皮倩瑛，葉洪濤.一種動態調節慣性權重的粒子群算法[J].廣西科技大學學報，2016，27（3）：26-32.

[17]? ?丁承君，閻欣怡，馮玉伯，等.基于APF的AGV局部路徑規劃改進算法研究[J/OL].計算機工程與應用，2021：1-10[2021-06-27]. https：//kns.cnki.net/kcms/detail

/11.2127.TP.20210420.1504.085.html.

[18]? ?YU X，YU Q. Enhanced comprehensive learning particle swarm optimization with dimensional independent and adaptive parameters[J].Computational Intelligence and Neuroscience，2021，2021（6）：1-16.

[19]? ?許家赫，陳岳坪.改進粒子群算法與fmincon函數混合尋優的平面度、垂直度誤差評定[J].廣西科技大學學報，2019，30（4）：105-109.

Longitudinal motion control of unmanned vehicle based

on IPSO-MPC

LI Guangnan1，3， YE Hongtao*1，2，3， LUO Wenguang1，3

（1.School of Electrical， Electronic and Computer Science， Guangxi University of Science and Technology，

Liuzhou 545616， China; 2. Guangxi Key Laboratory of Automatic Detecting Technology and Instruments （Guilin University of Electronic Technology）， Guilin 541004， China; 3. Guangxi Key Laboratory of Automobile

Components and Vehicle Technology （Guangxi University of Science and Technology）， Liuzhou 545006， China）

Abstract： A model predictive control method based on an improved particle swarm optimization? ? ? ? ?algorithm （IPSO） was proposed to solve the speed tracking accuracy problem in the longitudinal control of unmanned vehicles. Firstly， the model predictive control converted the problem into a quadratic? ? programming problem， used particle swarm algorithm to solve it， and implemented the speed tracking control through the layered longitudinal controller. The random weight strategy and the learning factor adjustment strategy were used to reduce the risk of falling into a local optimal solution. Secondly， the optimal particle sequence at the previous moment was preserved as the population extreme value of the particle at the next moment to improve the speed of particle searching. Finally， a co-simulation platform was established through Simulink/CarSim to verify the effectiveness of the algorithm. Simulation? ? ? ? results show that the algorithm effectively improves the control accuracy of vehicle speed tracking， and the maximum error is reduced by 0.274 7 km/h.

Key words： unmanned vehicle; model predictive control; particle swarm optimization; longitudinal control

（責任編輯：黎? 婭）