納米壓入法點陣分析金屬微觀組織力學性能

劉明， 徐智通， 高誠輝

(福州大學機械工程及自動化學院, 福建 福州 350108)

0 引言

納米壓痕技術具有操作方便、 樣品制備簡單、 測量和定位分辨率高(壓頭壓入材料表面的深度在納米尺度)、 測試內容豐富(如壓痕硬度[1]、 彈性模量[2]、 斷裂韌性[2-3]、 粘彈性[4]、 疲勞[5]、 蠕變[6-7]等)等優點， 是在微納米尺度， 壓頭在載荷作用下垂直壓入材料表面， 通過分析載荷-位移曲線獲得材料的微納米力學性能， 在材料的微觀力學性能研究領域有廣闊的應用前景， 廣泛應用于各種金屬[8-10]、 復合材料[11-13]、 高分子材料[14]、 陶瓷[15-16]、 薄膜[16-22]、 玻璃[23-26]等. 多相材料的單相態力學性能受到廣泛關注， 而眾多單相態不能以宏觀塊體的形式重現， 傳統力學測試方法(如單軸拉伸或壓縮)不再適用. 利用納米壓痕技術可以得到單一相態的微納米力學性能[27-28]， 但是有很大的局限性. 需要慎重選取最大壓入深度hmax， 過淺， 會放大單相態的表面粗糙度和組織不均勻性的影響， 降低實驗精度， 同時， 試樣近表面可能出現加工硬化現象(因在制樣時， 多使用多級砂紙水磨結合機械拋光的方法)[29]， 壓痕硬度會被高估； 根據膨脹腔理論[30]， 最大壓入深度hmax應小于相態特征長度尺寸D的1/10， 但表面下的單相態尺寸無法得知， 即使相對小的最大壓入深度hmax， 也可能受到基底效應的影響.

為實現對單相態的納米壓痕實驗， 需要對試樣進行金相腐蝕， 以便在光學顯微鏡下進行定位， 但金相腐蝕會顯著增大表面粗糙度甚至改變表層的化學性質， 而一些特殊的相態在光學顯微鏡下不可見或沒有合適的金相腐蝕液[31]. 即使是同相態， 不同的晶粒取向會影響力學性能， 單次納米壓痕實驗只能測定單個晶粒的力學性能. 當最大壓入深度hmax遠小于單相態特征長度尺寸D時， 通過對納米壓入法點陣數據進行多峰高斯擬合分析， 均值μi和標準差σi分別對應各相態的力學性能(如壓痕硬度HIT和彈性模量EIT等)的真實值和離散程度， 混合系數ci對應各相態面積分數， 即模型中各個擬合參數具有與之對應具有物理意義的量. 應用納米壓入法點陣研究的多相材料種類繁多， 如三元鋰電池陽極LiNi0.5Mn0.3Co0.2O2[32]、 混凝土、 骨頭和頁巖[33]、 海軍黃銅、 鑄鐵和M3高速鋼[31]、 軌道鋼[34]和水化硅酸鈣[35-36]等. Constantinides等[37]通過類比薄膜/基底模型， 發現納米壓入法點陣的壓痕尺度應是單相態組織特征長度尺寸的1/10， 與多相材料Ti-TiB納米壓入法點陣實驗結果吻合. 魏亞等[38]利用納米壓入法點陣方法研究摻雜不同礦渣含量水泥的各相態微納米力學性能和含量， 提出基于納米壓痕技術計算水化程度的方法， 與熱重分析得到的結果吻合. 沈俊達等[39]結合納米壓入法點陣和反卷積分析， 計算了水泥基材料微觀各相的斷裂韌性.

國內利用納米壓入法點陣分析雙相合金材料微觀組織力學性能的研究還報道較少. 本研究對3種黃銅(H59、 H60、 H62)和2種碳鋼(Q235鋼、 45#鋼)共5種常見且組織尺寸適中的雙相合金材料進行納米壓入法點陣實驗， 結合高斯混合模型， 確定材料微觀相態的力學性能(壓痕硬度HIT、 彈性模量EIT)和體積分數. 并在大載荷下對材料進行納米壓痕和努氏硬度實驗， 建立了宏觀和微觀力學性能的關系. 利用Image Pro-plus 6.0軟件[40-41]處理金相圖， 獲得體積分數fr， 驗證點陣實驗結果.

1 實驗原理

如圖1(a)所示， 加載時， 壓頭垂直壓入試樣表面， 材料發生形變， 產生接觸深度為hc、 接觸圓半徑為a的壓痕， 在一個完整加載-保載-卸載循環中， 得到如圖1(b)所示典型納米壓痕載荷-位移曲線. 利用經典Oliver-Pharr方法[42]根據載荷-位移曲線計算被測材料的微納米力學性能， 壓痕硬度HIT和縮減模量Er等微納米力學性能可由最大壓力Fmax、 最大壓入深度hmax、 接觸深度hc、 殘余深度hp和彈性接觸剛度S(卸載曲線的端部斜率)計算獲得.

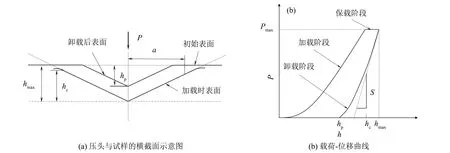
圖1 納米壓痕原理圖Fig.1 Principle schematic of nanoindentation

對卸載曲線進行擬合：

P=B(h-hp)m

(1)

其中：B為擬合常數；m為與材料相關的指數.

接觸深度hc為：

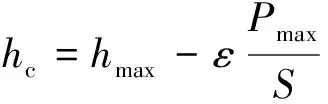
(2)

其中, 幾何常數ε取決于擬合參數m[25].

被測材料的壓痕硬度HIT為最大載荷Fmax與壓痕接觸投影面積Ac的比值,

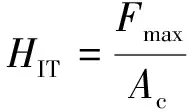
(3)

其中, 實際面積函數根據壓頭實際幾何形狀變化， 由力學性能已知的熔融石英測試結合B樣條插值擬合確定[23, 25].

被測材料的彈性模量EIT為：

(4)

其中：ν為被測材料的泊松比， 黃銅和碳鋼的泊松比分別為0.36和0.26[43]；E0=1 141 GPa、ν0=0.07分別為Berkovich金剛石壓頭的彈性模量和泊松比; 縮減模量Er為：

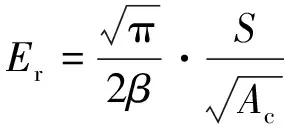
(5)

其中：β=1.034[44]為Berkovich金剛石壓頭形狀因子.

對于各相態隨機均勻分布的多相材料， 各相態微納米力學性能X(彈性模量EIT、 壓痕硬度EIT等)均服從高斯模型， 即X～N(μ,σ2).當壓頭在大載荷作用下垂直壓入材料表面， 最大壓入深度hmax遠大于單相態特征長度尺寸D時， 納米壓痕測得的是雙相態耦合的力學性能， 服從單峰高斯分布， 如圖2(a)所示. 當最大壓入深度hmax遠小于單相態特征長度尺寸D時， 點陣中單次納米壓痕測試結果更接近單相態的微納米力學性能， 服從雙峰高斯分布， 如圖2(b)所示.

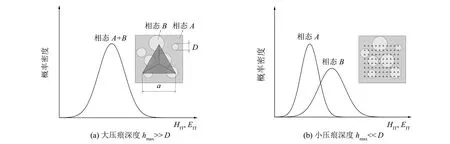
圖2 雙相合金的壓入法點陣原理示意圖Fig.2 Principle schematic of grid indentation technique in dual-phase alloy

混合高斯模型的概率密度函數為：

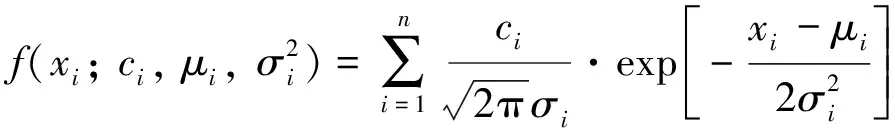
(6)

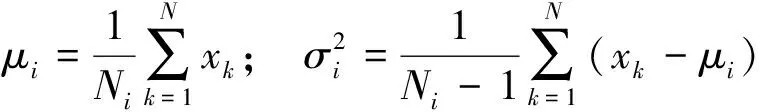
(7)

概率密度函數滿足：

(8)

式中：μi、σi和Ni分別為第i相態的平均值、 標準差和樣本空間；n為相態數， 對應高斯單峰的個數；ci為混合系數， 是i相態高斯峰的權重， 表示各相態的面積分數.對于各相態隨機分布的多相材料，ci被認為是體積分數， 滿足：

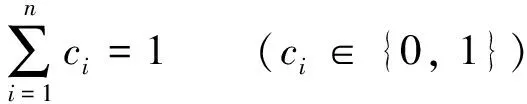
(9)

一個相對應3個未知數(μi、σi、ci)， 對X頻率直方圖的多峰高斯擬合求解， 可以獲得3n-1個未知量.

2 納米壓痕實驗

實驗前對材料進行預處理， 因化學金相腐蝕會改變近表面力學性能， 增大表面粗糙度， 需要制備2批試樣， 一批只進行磨拋， 用于納米壓入法點陣、 大載荷納米壓痕實驗和努氏硬度測定， 另一批在磨拋后進行化學金相腐蝕， 用于對單相態進行組織觀察確定點陣實驗參數以及進行獨立納米壓痕實驗. 選用德國勇士SiC水磨砂紙對材料進行水磨至3 000#. 當表面劃痕深淺一致且方向相同時， 選用恒宇公司生產的金剛石拋光膏進行機械拋光， 直到材料表面無劃痕且呈鏡面效果， 在丙酮溶液中超聲清洗去除表面雜質. 配制比例為FeCl3∶HCl∶H2O = 5 g∶10 mL∶100 mL的黃銅腐蝕劑， 在室溫下對黃銅進行約1 min的腐蝕， 配制5%的硝酸酒精溶液， 在室溫下對碳鋼進行約10 s的腐蝕， 腐蝕后立即用去離子水沖洗材料表面的腐蝕液. 光學顯微鏡觀察的試樣表面無麻點、 組織區分明顯、 晶界清晰. 試樣制備完成后， 立即放入恒溫干燥箱中密封保存.

在納米壓痕儀配備的光學顯微鏡下可以任意選定某單相態區域， 在滿足最大壓入深度hmax小于單相態的特征長度尺寸D的1/10的條件下[37, 45]， 確定實驗最大載荷Fmax， 在相態中心進行壓痕實驗獲得單一相態的力學性能. 3種黃銅的銅鋅比例不同，α相和β相的體積分數不同， 但兩相態的微觀力學性能相同， 只對H59黃銅進行單相態獨立的納米壓痕實驗， 而碳鋼因含碳量和成型條件不同， 每種碳鋼的珠光體和鐵素體的含量和力學性能可能有很大差異， 對兩種碳鋼均進行獨立納米壓痕實驗.

選用美國Anton Paar公司的NHT2型納米壓痕儀對材料進行點陣實驗， 壓頭為Berkovich金剛石壓頭. 選用美國FEI公司的QuantaTM250 FEG型掃描電子顯微鏡對金相腐蝕后的試樣表面成像， 觀察各相態的組織尺寸和分布情況， 5種材料的相態特征長度尺寸均在10 μm以上. 選取與獨立實驗相同的載荷， 壓痕間距l應盡量靠近各相態的特征長度尺寸， 且大于最大壓入深度的20倍， 確保相互之間無干涉[46-47]， 試驗次數N等參數列于表1.

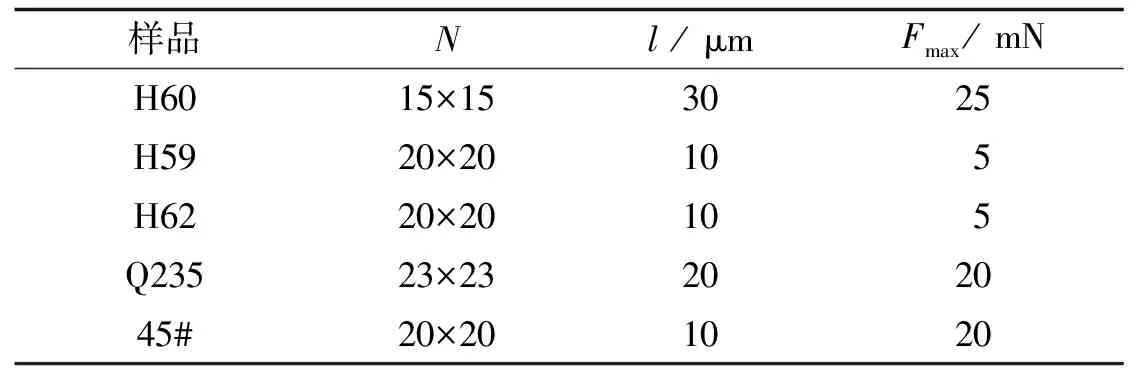
表1 納米壓痕實驗參數

在500 mN大載荷下對材料進行壓痕實驗, 獲得材料宏觀力學性能. 當最大載荷為5 mN時， 加載和卸載時間為10 s， 保載時間為5 s， 采樣頻率為30 Hz； 當最大載荷大于5 mN時， 加載和卸載時間為30 s， 保載時間為10 s， 采樣頻率為10 Hz. 利用上海鉅晶的MHVKD-1000型微米硬度計， 測定材料的努氏硬度Hk， 載荷為300g(2.94 N)， 保載時間為15 s.

3 實驗結果與分析

3.1 單相態納米壓痕實驗

利用Image Pro-plus 6.0軟件處理化學金相腐蝕過的H59黃銅的掃描電鏡(SEM)圖. 首先將圖片轉化為8位灰度圖， 用“Despeckled”工具去除孔洞， 然后調節圖像的對比度、 亮度和伽馬值， 結果如圖3(a)所示.α相是Zn在Cu中的固溶體，β相是以電子化合物CuZn為基的固溶體. 利用SEM的X射線能譜分析(EDS)測定單相態中的原子比例, 見圖3(a)插圖(為直觀比較兩相中的銅鋅質量分數，β相向右偏移了1 keV)， 測得α相中Zn質量分數為34.62%，β相中Zn質量分數為41.71%， 與張文達等[48]的研究結果一致. Zn的耐腐蝕性較差，α相較β相的耐腐蝕性強[49-50]， 組織形貌較化學金相腐蝕前沒有太大改變,β相組織被均勻腐蝕， 表面粗糙度變大. 圖3(b)為45#鋼的金相圖， 鐵素體為白色塊狀組織， 珠光體為鐵素體和黑色滲碳體交替分布的片層組織. 所有材料的相態特征長度尺寸D均在10 μm以上.

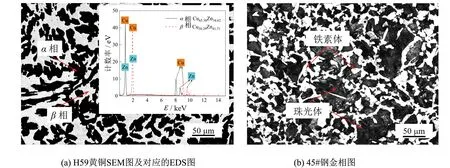
圖3 Image Pro-plus 6.0處理的材料微觀組織圖Fig.3 Image Pro-plus 6.0-processed microstructure images

圖4為H59黃銅和45#鋼各相態典型的納米壓痕實驗的載荷位移曲線. 各相態力學性能等參數值列于表2， 平均最大壓入深度hmax均滿足hmax/D<0.1， 符合要求[37]. H59黃銅的α相比β相的壓痕硬度和彈性模量低， 但差別較小， 可能是兩相的銅鋅比例相近. 碳鋼珠光體比鐵素體壓痕硬度高， 與張罡等[51]研究結果相同， 鐵素體的彈性模量約為255 GPa， 與朱勝等[52]的研究結果相同， 兩種碳鋼的同種相態的硬度及彈性模量相同.

圖4 獨立納米壓痕的典型載荷-位移曲線 Fig.4 Typical load-displacement curves of isolated nanoindentation

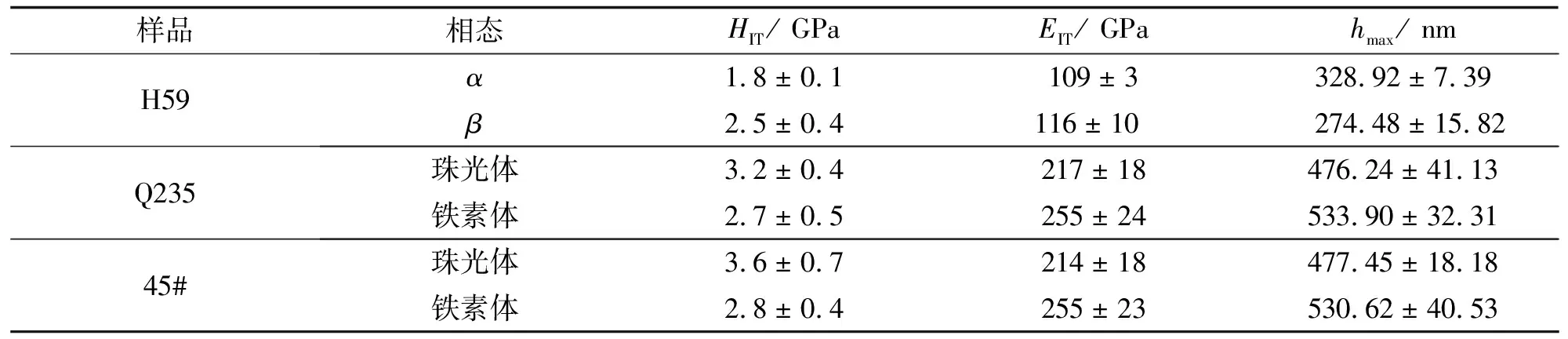
表2 H59黃銅、 Q235鋼和45#鋼的單相態獨立納米壓痕實驗結果

3.2 納米壓入法點陣

組織間相互影響， 力學性能有過渡區域， 相界可以被視為一個特殊的相態[53]， 發生在異相態間晶界及其周圍區域， 稱為相界效應. 3種黃銅納米壓入法點陣實驗壓痕硬度HIT和彈性模量EIT的頻率直方圖如圖5所示.

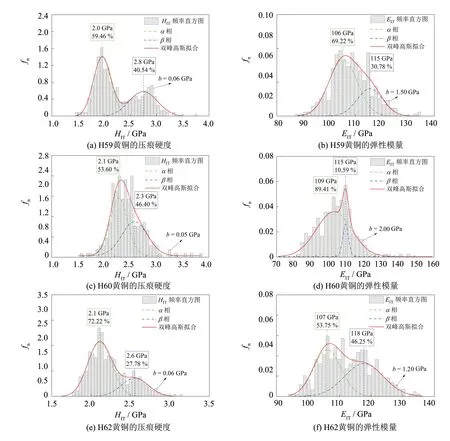
圖5 黃銅壓痕硬度HIT和彈性模量EIT頻率直方圖的高斯模型擬合 Fig.5 Gaussian distribution fitting results of the HIT and EIT histograms of H62 brass

對頻率直方圖的高斯混合模型的擬合結果為概率密度曲線， 積分為1(公式(8))， 因此頻率直方圖的面積和應為1， 縱坐標為相對頻數， 應除以組距b(bin size， 標于圖中)， 表示標準化概率密度fn. 頻率直方圖均有兩個較明顯的峰， 黃銅的α相和β相的壓痕硬度HIT以及彈性模量EIT差異較小(見表2)， 相界效應可以忽略， 應該利用雙峰高斯模型進行擬合. 擬合參數μi、σi對應各相態壓痕硬度HIT和彈性模量EIT的均值和標準差見表3.

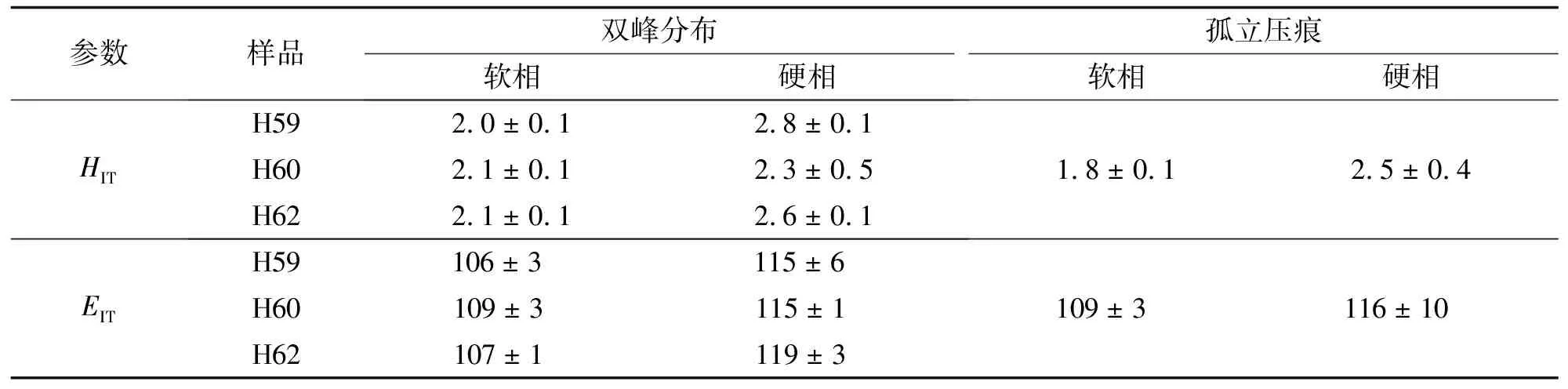
表3 雙相黃銅的單相態壓痕硬度HIT和彈性模量EIT

不同黃銅材料中同相態力學性能(壓痕硬度HIT和彈性模量EIT)相同， 但均略大于單相態獨立壓痕實驗得到的結果， 這是因為對材料進行化學浸蝕可以去除部分表面加工硬化層[27]， 彈性模量EIT對組織不敏感， 受加工硬化的影響不大， 因此與單相態獨立壓痕實驗的結果一致. H60黃銅β相的壓痕硬度略小于單相態獨立壓痕實驗結果， 可能是由于點陣實驗數據較少.

兩種碳鋼點陣實驗得到的壓痕硬度HIT和彈性模量EIT頻率直方圖如圖6所示. 圖6(a) (b)均有明顯的2個單峰， 雙峰高斯模型擬合硬度較小的單峰結果與鐵素體獨立壓痕結果一致， 而另一單峰的擬合值小于珠光體獨立壓痕結果. 45#鋼含碳量為0.45%， 其中珠光體組織平均含碳量為0.77%， 鐵素體組織的平均含碳量為0.021 8%.

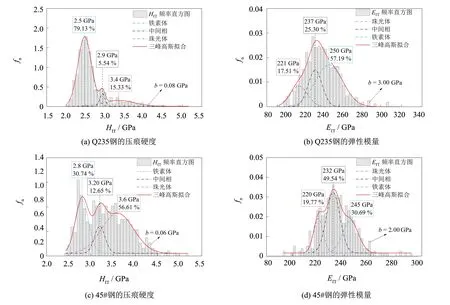
圖6 碳鋼壓痕硬度HIT和彈性模量EIT頻率直方圖的三峰高斯模型擬合Fig.6 Trimodal Gaussian distribution fitting results of the HIT and EIT histograms

利用三峰高斯模型擬合得到的壓痕硬度HIT與單相態獨立壓痕實驗結果見表4. 根據杠桿原理[54]， 45#鋼的珠光體體積分數ωp(ωp=(0.45-0.021 8)/(0.77-0.021 8)=0.57) 遠小于壓痕硬度雙峰擬合得到的珠光體0.92的體積分數， 表面相界效應存在， 雙峰的高斯模型擬合不適用鐵素體和珠光體差異比較大的壓痕硬度HIT和彈性模量EIT.

表4 碳鋼的單相態和塊體的壓痕硬度HIT和彈性模量EIT

點陣實驗的接觸深度hc和殘余深度hp均隨最大壓入深度hmax的增大而線性增加， 與材料種類無關， 僅與納米最大載荷Fmax有關， 如圖7所示.

圖7 實驗參數與最大壓入深度hmax的關系Fig.7 Variation of depth with increasing maximum indentation depth hmax

3.3 單相態體積分數

H59黃銅微觀組織圖中任意選取的區域面積足夠大見圖3(a)， 以獲得更接近整體的相態分布. 利用“Measure”工具測量α相和β相的面積分數， 等效為體積分數fr列于表5.

觸剛度S、 壓痕彈性功We(卸載曲線下的面積)、 壓痕總功Wt(加載曲線下的面積)和4β2Pmax/(πS2)的頻率直方圖得到的各相態體積分數，fr為利用Image Pro-plus 6.0對金相圖的分析結果， 加粗數據表示與fr接近.

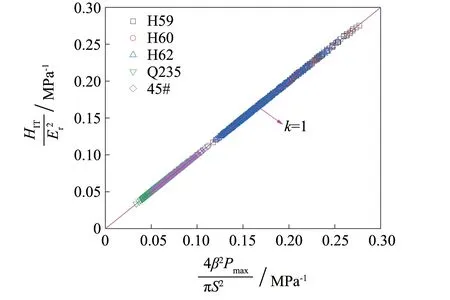
圖與4β2Pmax/(πS2)的關系 Fig.8 Variations of with increasing 4β2Pmax/(πS2)

由公式(3)和(5)可推導得：

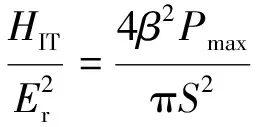
(10)

4β2Pmax與接觸面積Ac無關， 將材料的點陣數據帶入公式(11)， 發現等式成立(見圖8). 利用雙峰高斯混合模型對4β2Pmax/(πS2)和各種力學性能參數(比如： 壓痕硬度HIT彈性模量EIT等)的頻率直方圖擬合， 雙峰均較為明顯， 得到的兩相體積分數也列于表4. 而對4β2Pmax/(πS2)頻率直方圖進行雙峰高斯擬合得到的體積分數fc與利用Image Pro-plus 6.0對金相圖分析得到的體積分數fr接近， 這是由于壓頭磨損導致面積函數發生改變. 彈性功We和總功Wt的頻率直方圖雙峰擬合得到的各相態體積分數fwe和fwt與fr接近， 這是由于材料的各相態的彈性功及總功相近， 相界效應不明顯. 其他參數頻率直方圖雙峰擬合結果對個別材料適用， 沒有普適性， 僅可用以定性比較.

將體積分數fr作為雙峰高斯混合模型擬合的混合系數ci， 對黃銅的雙峰高斯擬合結果列于表6.α相和β相的壓痕硬度和彈性模量的擬合值與未設定混合系數ci得到的結果一致， 可能是由于實驗數據不夠多， 高斯峰不明顯， 可得到準確的力學性能， 但對體積分數的擬合存在偏差， 而點陣數據較多的海軍黃銅可以得到較準確的體積分數[31].

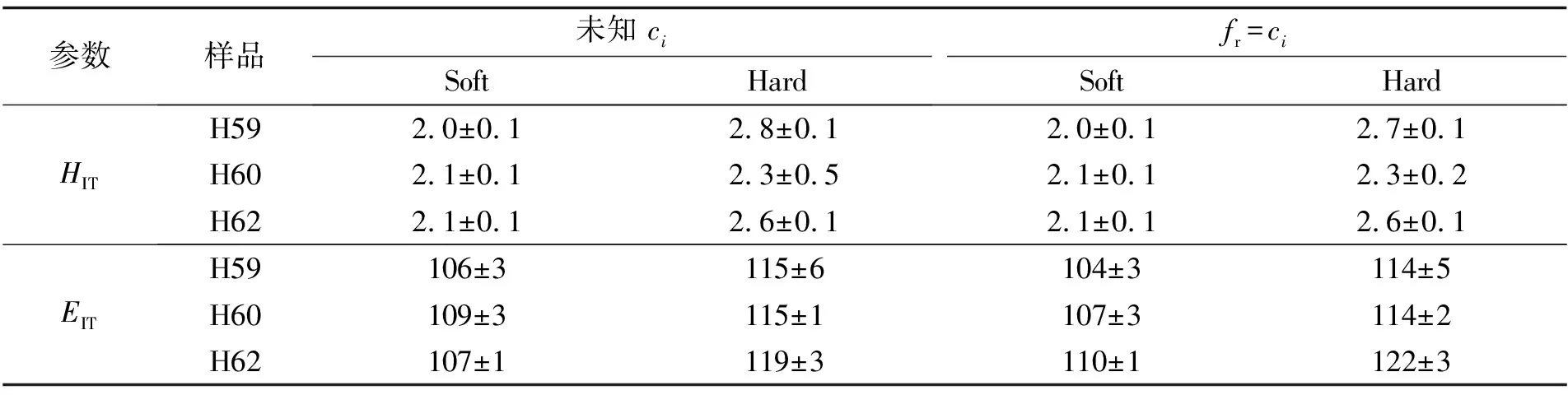
表6 混合系數ci未知和fr為已知混合系數ci的雙峰高斯擬合的黃銅壓痕硬度和彈性模量對比

利用高斯混合模型對壓痕硬度和彈性模量的頻率直方圖擬合得到各相態體積分數已有報道[31, 55]， 但是本研究結果有一定的適用范圍， 各相態間的相界效應是主要的影響因素. Matthieu等[31]對兩相材料Ti64-10TiC進行納米壓入法點陣實驗， 兩相的壓痕硬度和彈性模量差距較大， 頻率直方圖有明顯的由于相界效應導致的過渡單峰， 雙峰擬合不適用， 與本研究的碳鋼類似. 當材料各相態硬度較高、 相態間的硬度和彈性模量相互之間的差異明顯、 相界效應影響較小(如陶瓷材料)時， 頻率直方圖的雙峰沒有重疊， 利用點陣實驗和高斯混合模型可獲得準確的各相態體積分數[37, 55].

表7為不同實驗載荷下得到的黃銅和碳鋼壓痕硬度和彈性模量. Knoop壓頭與Berkovich壓頭幾何形狀不同， 但測定材料顯微硬度均是利用載荷除以投影面積， 且在相同載荷下得到的金屬和非金屬材料的顯微硬度具有一致性[56]， 努氏硬度還可用于非晶材料的彈性模量、 屈服強度的測量和尺寸效應的研究[57]. 黃銅和碳鋼均表現出壓痕硬度隨載荷增大而減小的趨勢， 可能是壓痕尺寸效應(材料的壓痕硬度隨載荷的增加而降低[58-59])， 也可能是表面加工硬化的影響. 黃銅的α相和β相壓痕硬度差異較小， 隨α相的增加， 宏觀硬度沒有明顯變化， 碳鋼壓痕硬度隨珠光體含量的增加而增加.材料的Eave略小于Em， 定義誤差率e為：

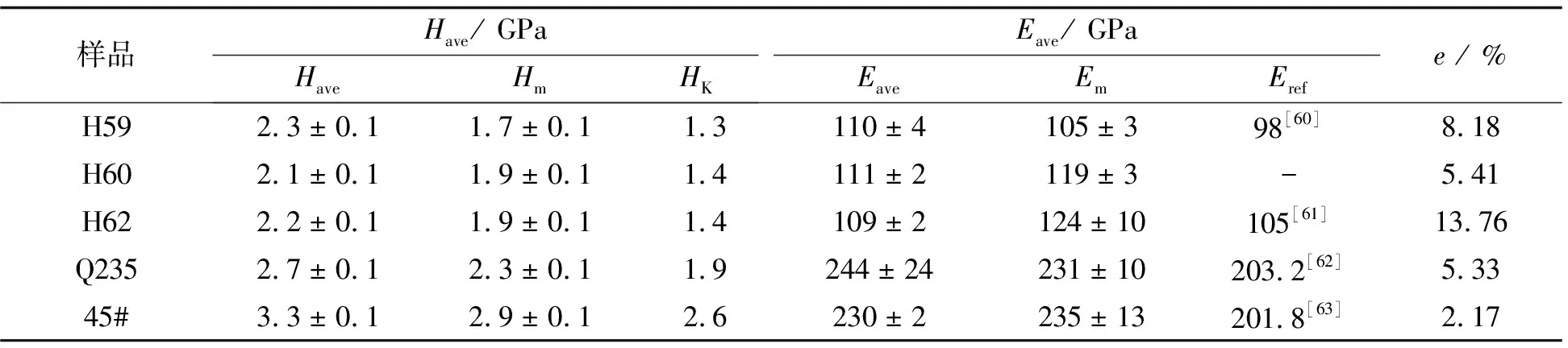
表7 不同實驗條件下黃銅和碳鋼壓痕硬度和彈性模量對比

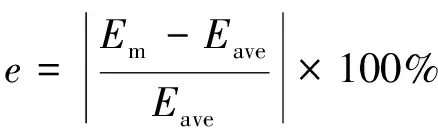
(11)

其中： 誤差率e最大為13.76%， 說明Eave接近真實的宏觀塊體的壓痕彈性模量.

納米壓痕法測量得到的彈性模量高于常規拉伸試驗得到的彈性模量(如單軸拉伸實驗測得45#鋼的彈性模量為201.8 GPa， 小于納米壓痕實驗得到的244.0 GPa[63]), 其主要是測試中的壓頭尖端的形狀、 被測材料表面粗糙度、 接觸定位零點等因素的影響.

4 結語

使用Berkovich壓頭對三種黃銅和兩種碳鋼進行納米壓入法點陣實驗， 結合高斯混合模型統計方法評估微觀組織力學性能和體積分數， 主要結論如下：

1) 黃銅兩相(α相和β相)的同種力學性能(壓痕硬度和彈性模量)差異很小， 雙峰高斯模型擬合結果與單相態獨立壓痕結果一致. 而碳鋼的兩相(鐵素體和珠光體)同種力學性能差距較大， 相界效應的影響不能忽略， 三峰高斯混合模型得到的壓痕硬度和彈性模量與單相態獨立壓痕結果一致.

2) 材料的各相態同種力學參數(彈性功We、 總功Wt和4β2Pmax/(πS2))接近， 對彈性功We、 總功Wt和與接觸面積無關的4β2Pmax/(πS2)的頻率直方圖的雙峰高斯模型擬合的fwe、fwt和fc與Image Pro-plus 6.0軟件得到的體積分數fr接近. 其余各項參數(壓痕硬度HIT、 彈性模量EIT、 擬合指數m、 最大壓入深度hmax和接觸剛度S)的分析得不到準確的體積分數.

3) 壓痕硬度隨最大載荷的增大而減小， 表現出明顯的尺寸效應. 納米壓入法點陣得到的加權彈性模量Eave和大載荷下壓痕實驗得到的彈性模量Em接近， 納米壓痕的彈性模量大于單軸拉伸得到的彈性模量Eref.