公路貨運場站車貨動態配載優化研究

張 赫，王 宇，劉 宇，邢江豪

(大連海事大學 交通運輸工程學院，遼寧 大連 116026)

0 引 言

交通運輸業是國民經濟的主導性產業，黨的十九大明確提出了建設交通強國的口號，而公路運輸在各種交通運輸方式中占據著重要地位，2018年公路貨物運輸量為395.9 億噸，同比增長7.4 %，占貨物運輸總量的76.9 %。近年來，隨著我國經濟的不斷發展，大城市外來人口的不斷涌入，導致了交通不暢和擁堵，加大了城市公路物流業的負擔。貨車常常因為道路堵塞而延誤到達貨運場站取貨的時間，同時由于運輸企業對于車輛配貨的調度安排經常是根據自身經驗，缺乏合理的方法，導致車輛與貨物之間無法有效配載，車輛空駛率高。因此，如何有效預測貨車的周轉行程時間，使得貨運場站能夠提前掌握返回車輛的信息，根據車輛和貨物的動態信息制定配載方案，最大程度的利用貨車資源，減少人力物力的浪費，提高貨運場站的經濟效益是目前亟待解決的問題。

在車輛行程時間預測方面，H.M.MOONAM等[1]使用K最近鄰、最小二乘回歸增強和卡爾曼濾波等方法從已有的數據預測未來的行程時間，并得出了卡爾曼濾波在基于道路的模型中有著更好的預測精度；R.X.ZHONG等[2]提出了一個在線行程時間預測模型，重點是捕捉異常的影響；景輝鑫等[3]針對交通流數據波動性較高和易失真的缺點，提出一種基于灰色 ELM 神經網絡的短時交通流預測方法；溫惠英等[4]針對行程時間波動性加入了機動車和非機動車因素，建立了阻抗函數模型；潘義勇等[5]將城市交通道路阻抗分為路段阻抗與節點阻抗兩部分，分別建立模型并利用道路阻抗影響因子進行改進。

在車貨配載方面，張嘉寧[6]建立了大宗商品配載問題的組合優化數學模型；L.BAJRACHARYA[7]提出了一種對分散的物流貨車和貨物進行最優路徑分配的管理方法；李建民等[8]就車貨配載問題建立了包括車輛空駛率最小、利用率最大等多目標規劃模型；徐天亮等[9]建立了單車和多車配裝兩個數學模型并給出了算法；陳宏程[10]將車貨配裝和配送路徑問題結合起來，設計了一種自動選擇車輛類型，配載聯合優化模型；侯景瑞等[11]從車主角度出發，以車主收益最高為目標函數，建立了貨車配載模型，并用改進的遺傳算法進行了求解；S.A.BJORGEN等[12]提出了智能貨物這個新概念，以實現貨源方和車源方在運輸網絡中的無縫互連；D.GATTUSO等[13]建立了一個隨機的離散事件仿真模型來解決與車輛和貨物接收相關的問題。

陸丹[14]以車輛數最小為目標，建立了靜態車貨配裝優化模型并進行了求解；張赫等[15]建立了車輛動態配貨模型并用Visual Basic軟件進行了模擬。文獻[14-15]都只考慮到了車輛與貨物的一次配裝，無法及時有效地對動態變化的車貨配載問題進行求解。筆者重點在前兩者的研究基礎之上，結合車輛行程時間預測，并加入了對車輛維修保養因素的考慮，建立了動態車貨配載模型。根據不同時間段貨運場站內的貨車類型和數量，對車輛和貨物的配載方式進行了優化，以提高車輛利用率，優化貨車資源配置，有利于貨運場站做出更快、更有效的調度決策。

1 影響因素分析

1.1 貨車周轉行程時間

周轉時間為貨車從貨運場站出發，到達目的地卸貨和返程時間的總和。行程時間會受到各個路段交通流量、意外交通事故和天氣原因等的影響，因此其為一個不確定值。通過對貨車周轉時間的預測，可以使貨運場站實時掌握車輛動態信息，及早為預到達的車輛準備停車區以及相應工作人員和貨物裝卸設備，提高貨運場站裝卸效率，減少不必要的調度成本。因此筆者需要收集交通流量、車輛數以及行駛時間等參數。在交通流量收集方面，筆者采用人工觀察法；在行程時間收集方面，采用GPS定位方法和人工記錄方法相結合的辦法，GPS接受信息后將數據傳入計算機，從而根據行駛里程和駕駛速度計算出平均行駛時間，然后再采用人工方法用秒表記錄堵車狀態下的延誤時間，再在表格分別記錄下來，最后進行加和處理即為總的行程時間。周轉時間包括3個部分：路段行駛時間用T1表示、交叉口延誤時間用T2表示、目的地卸貨時間用T3表示。可用公式表示為:

T=T1+T2+T3

(1)

根據定義，車輛交通占用率值等于路段上車輛的平均總長度與路段長度之比，如式(2):

(2)

該公式可轉換為:

(3)

式中：γ為路段交通占有率；S為時段內路段上平均車輛數；a為標準車的長度，可取敞車、篷車和平車長度的平均值；L為路段長度。

通常情況下，城市交通網絡在固定時期(一年或幾個月)內幾何線形不會發生重大的變化，交通需求情況較穩定或變化緩慢，可以大致認為日常交通流的時空分布也比較穩定，從而各路段上交通流的幾何線形可視為固定的[16]。分別將S和W視為關于t的函數，當所預測的時間距當前時刻較近時，利用泰勒公式可得公式為:

S(t)=S(t0)+S′(t0)Δt

(4)

W(t)=W(t0)+W′(t0)Δt

(5)

式中：S(t)和W(t)分別為所要預測時段內車輛數和預測時段內交通流量值(機動車、非機動車和行人)；S(t0)和W(t0)分別為車輛通過時段路段上的車輛數和交通流量值；S′0(t0)為過去幾天同一時段內車輛數平均值；W′0(t0)為過去幾天同一時段內交通流量值；Δt為所要預測的時段距車輛通過時段的時間間隔。

1.1.1 路段行駛時間

路段行駛時間是指貨車從貨運場站裝貨出發到周轉返回貨運站未發生堵車所耗費的時間T1，文中為車輛來回時間，認為來回行駛時間相同，可以用式(6)表示:

(6)

式中：T1為路段行駛時間；L為路段長度；V為貨車行駛的平均速度。

1.1.2 交叉口延誤時間

交叉口延誤時間是由于交叉口交通流量過大，發生意外交通事故和天氣原因等的影響導致車輛在交叉口逗留所耗費的時間T2。延誤時間包括去時和回時兩部分延誤時間，可以用式(7)表示:

T2=S1Δt+S2Δt

(7)

式中：Δt為抽樣時間間隔；S1為去時出口交通量；S2為回程出口交通量。

1.1.3 卸貨時間

研究的卸貨時間可以按照理想化處理，認為每種車型裝卸同一種貨物的時間是相同的。

1.2 貨車周轉及保養維修因素

公路貨運場站車貨配載研究需要考慮每次參與運輸的車輛周轉及保養維修因素，該因素會對運輸任務產生影響。在進行車貨調度時，參與運輸任務出發以及需要保養維修的車輛會導致場站現有貨車數量減少，而周轉車輛以及完成維修保養車輛的返回又會使場站現有貨車數量增加，進而對下一次運輸任務的車貨調度帶來影響。這時候就需要貨運場站提前調整運輸計劃，合理進行貨車資源分配。

1.3 動態配載基本思想

公路貨運場站的車輛與所需要運送的貨物都是動態變化的。貨運場站的貨車數量可能會由于臨時的抽調或者車輛的周轉返回而有所變化，甚至包括車輛所出現的維修保養等因素都會對其產生影響，而貨運場站的貨物由于每批車輛的運送也會發生改變。這兩者的不斷變化意味著車貨配載并不是一個一次優化，而是一個多次優化的動態過程。場站車輛的變化會影響對于貨物的配載方案，貨物經過每次裝車后的變化又會影響到貨運場站對于不同車型和數量的需求，兩者之間是一個相互影響、相互反饋的關系。

2 車貨動態配載優化模型

2.1 問題描述

貨運場站通常有不同種類的貨物等待運輸，場站不同時刻分批次派出不同類型的車輛進行配載運輸任務，不同類型的貨車對于所裝取的貨物有各自的技術定額要求。在訂單已下達，需要滿足貨運要求的情況下，同時考慮到周轉車輛的返回以及貨車保養維修等因素，如何進行動態調度研究使得所需的車輛數最少，優化車輛資源配置是筆者主要研究的問題。

通過應用車輛周轉行程時間的預測結果，推測出未來時刻周轉返回公路貨運場站的車輛類型和數量，并建立了動態車貨配載模型，以車輛數最小為目標函數，合理分配不同批次貨車所裝運的貨物數量，以減少貨車資源浪費，提高場站運作效率和經濟效益。

2.2 問題假設

1)參與運輸任務的貨車為貨運場站自備車輛，不需要運輸公司參與。

2)卸貨時間按照理想化處理，認為每種車型裝卸同一種貨物的時間是相同的。

3)不考慮貨運場站堆場空間和裝卸約束限制，即認為每批貨車同時開始裝卸和運輸任務，不需要等待。

4)周轉返回的貨車如果遇到突發狀況例如保養維修等因素無法參與下一階段運輸任務，會進行修理并等待下一階段運輸任務結束后重新加入。

5)不考慮貨車在運輸途中所發生的突發故障或事故。

2.3 模型建立

2.3.1 目標函數

本模型以車輛數最小為目標函數，該模型可以用公式表示為:

(8)

式中：m為貨車車型數；n為貨物種類；t為派出車輛的累計批次；xijk為第k批i型貨車運送j種貨物的車輛數。

2.3.2 約束條件

(9)

(10)

0≤wijk≤1 (?i∈1,2,…,m?j∈1,2,…,n

?k∈1,2,…,t)

(11)

(12)

Ai(k+1)≤dik(?i∈1,2,…,m?k∈1,2,…,t)

(13)

T1k+T2ki≤T3ki(?i∈1,2,…,m?k∈1,2,…,t)

(14)

Arik+gi(k+1)-Ai(k+1)=Ari(k+1)

(?i∈1,2,…,m?k∈1,2,…,t)

(15)

(16)

(17)

(18)

(19)

(20)

xijk≥0,pij≥0,Aik≥0,Qik≥0,dik≥0

(21)

式中：Ai為貨運場站所擁有的i型貨車的初始數量；Aik為第k批發出的i型貨車的數量；Arik為第k批貨車發出后i型車的剩余數量；Qj為j種貨物的初始數量；Qjk為第k批車輛裝運前j種貨物的剩余數量；pij為i型車裝運第j種貨物的技術定額；wijk為第k批i型車輛運送j貨物的實載率；dik為第k批車輛運走后重新規劃下一批i型貨車的需求量；gik為第k批任務開始前由于周轉車輛的返回或保養維修等因素引起i型車數量的變化值；T1k為第k批任務開始時間；T2ki為第k批車輛i在貨運場站的裝貨與周轉行程時間的總和；T3ki為第k批車輛i返回貨運場站后距離最近的下次任務開始時間。

在上述模型中：式(8)為目標函數，求得所有批次車輛運送完全部貨物所需的車輛數最小值；式(9)為每批次貨車運送的貨物類型不得超過該貨物所剩余的最大值；式(10)為保證所有貨物都被裝運；式(11)為貨車的實載率約束，不可以超載運輸；式(12)為每批次發出的貨車都被安排進行貨物運輸；式(13)為貨運場站每批次發車的各車型數量不得大于上一批結束后計算所得出的剩余貨物所需各車型的數量；式(14)為車輛周轉行程時間約束，表示周轉返回的車輛會加入下一次運輸任務的調度中；式(15)為貨運場站第k批剩余車輛與第(k+1)批剩余車輛之間的變化關系；式(16)為裝運完全部貨物所需的車輛數不得超過貨運場站所提供的總車輛數，總車輛數會受到周轉車輛返回以及車輛保養維修等因素的影響；式(17)為根據貨車的車型有些貨物無法進行裝運；式(18)為優先度高的貨物優先進行裝運；式(19)和式(20)為決策變量；式(21)表示這些變量為非負整數。

3 算法設計

解乘數法是列奧尼德·康托羅維奇于1938年第一次提出，用于求解線性規劃的方法，比1947年George Dantzig所發明的單純形法早了將近10年。解乘數法為合理地組織生產和計劃方式提供了開闊的應用前景，被廣泛應用于有效地組織貨物運輸，合理分配機器作業等問題中。將解乘數法應用于車貨配載問題中，確定初始方案，并且通過一系列變化規則來改變配載方案，對于一個實例，由于其基本可行解是有限的，所以最終可以得到該問題的最優解。采用解乘數法來對該模型進行求解，動態優化每批車輛運送的貨物，具體的步驟如圖1。

步驟1確定初始方案

對于每一種貨物，選取技術定額p最大的貨車進行分配，如果該類型貨車全部分配完后仍有貨物，則選取技術定額第二大的貨車，以此類推直到貨物全部分配完成。

步驟2計算剩余、不足行

計算貨運場站內每一種車型的剩余、不足行。剩余、不足行等于現有各類車型的車輛數減去已分配的車輛數，其值為正屬于剩余行，其值為負屬于不足行。如果差值為0則分為兩種情況討論，如果該車型對于某種貨物的技術定額與其它屬于不足行的車型的技術定額相同，且該不足行車型已經分配了此種貨物，則該車型為不足行，否則為剩余行。如果所有行都為剩余行，就說明此方案已達到最優，如果有不足行則代表還需要繼續優化。達到最優后跳轉到第7步，貨物全部裝運完成則結束。

步驟3計算解乘數值

每種貨物的解乘數值r等于各個車型屬于不足行的最大技術定額除以屬于剩余行的最大技術定額。如果屬于不足行的貨車對該種貨物沒有分配，則不必計算r，在所有r中選出最小的值rmin。

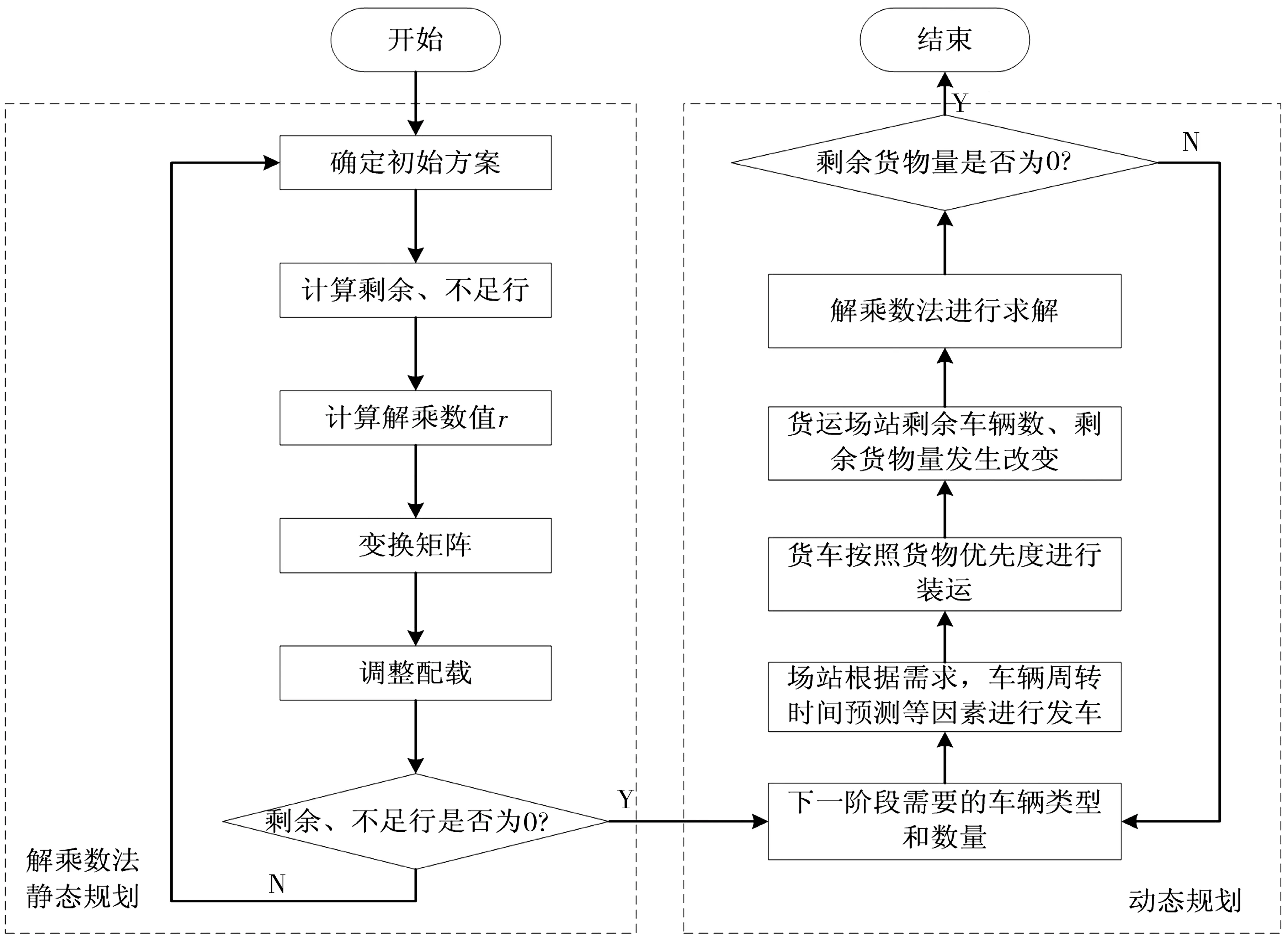
圖1 算法流程Fig. 1 Algorithm flow

步驟4變換矩陣

如果剩余行的數量大于不足行的數量，就用不足行的各個技術定額除以rmin，代替原來p值；反之，則用剩余行的各個技術定額乘以rmin，代替原來p值。

步驟5調整配載

將rmin中屬于不足行，且已經分配的貨物的全部(或部分)轉移給屬于剩余行且技術定額最大的貨車，使得車輛不足的問題得以消除。

步驟6對調整過后的配載方案，重復步驟2～步驟5，直到得到最優方案。

步驟7根據前面解乘數法的優化結果，得出完成剩余貨物所需的各個車型以及對應車輛數。場站根據自身情況進行安排，決定下一批次進行運輸任務的車型和數量。

步驟8貨車根據貨物優先度進行裝運，貨物優先度由場站根據客戶要求以及自身情況所決定。裝運并發車后，計算場站內剩余貨物量，以及在下一批車輛調度計劃制定之前，周轉車輛的返回以及保養維修所造成的貨車數量變化。最后跳轉到步驟1，對下一批車貨配載進行優化。

其中，步驟1～步驟6是解乘數法對于一次車貨配裝的優化求解過程。通過步驟7、步驟8，調整每次配貨后車輛以及貨物的變化參數，將一次配裝過程進行循環往復，進而實現了基于解乘數法的動態車貨配載優化。

4 算例分析

4.1 算例描述

為了檢驗模型和算法的有效性，筆者給出算例分析。大連某貨運場站到目的地距離為4 km，所有發往目的地的車輛都沿一條道路行駛，貨車以平均36 km/h車速自由行駛，交叉口堵車距離大約為200 m。貨運場站待運貨物種類和噸數，車種數量以及技術定額如表1。貨物運送優先度根據客戶需求決定，為鋼材>水泥>混凝土>花崗巖>大理石>瓷磚，貨運場站的貨車在技術定額允許的情況下，按照優先度順序進行裝運。場站共計發車6批完成所有運輸任務，每批出發的車輛類型和數量由貨運場站根據每次解乘數法求解得出的需要車輛數進行安排，具體見表3～表8。車輛周轉行程時間預測如表2，裝卸時間為車輛在貨運場站的裝貨時間和到達目的地的卸貨時間的總和。

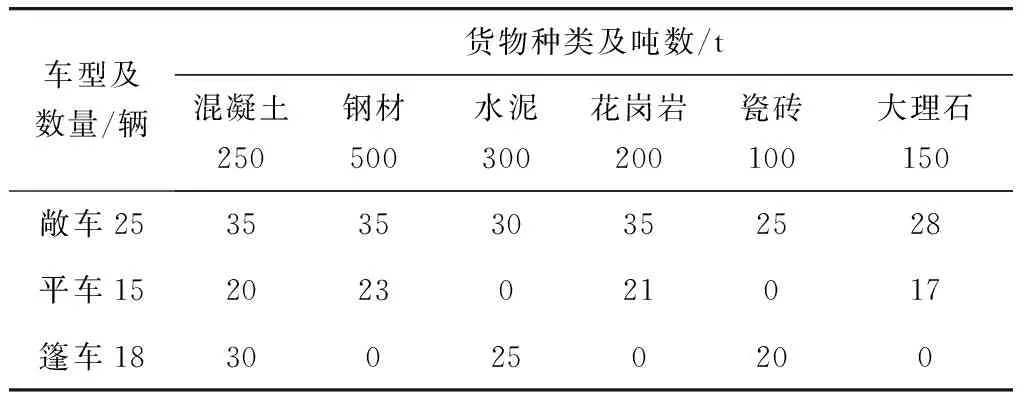
表1 車輛技術定額Table 1 Vehicle technical quota

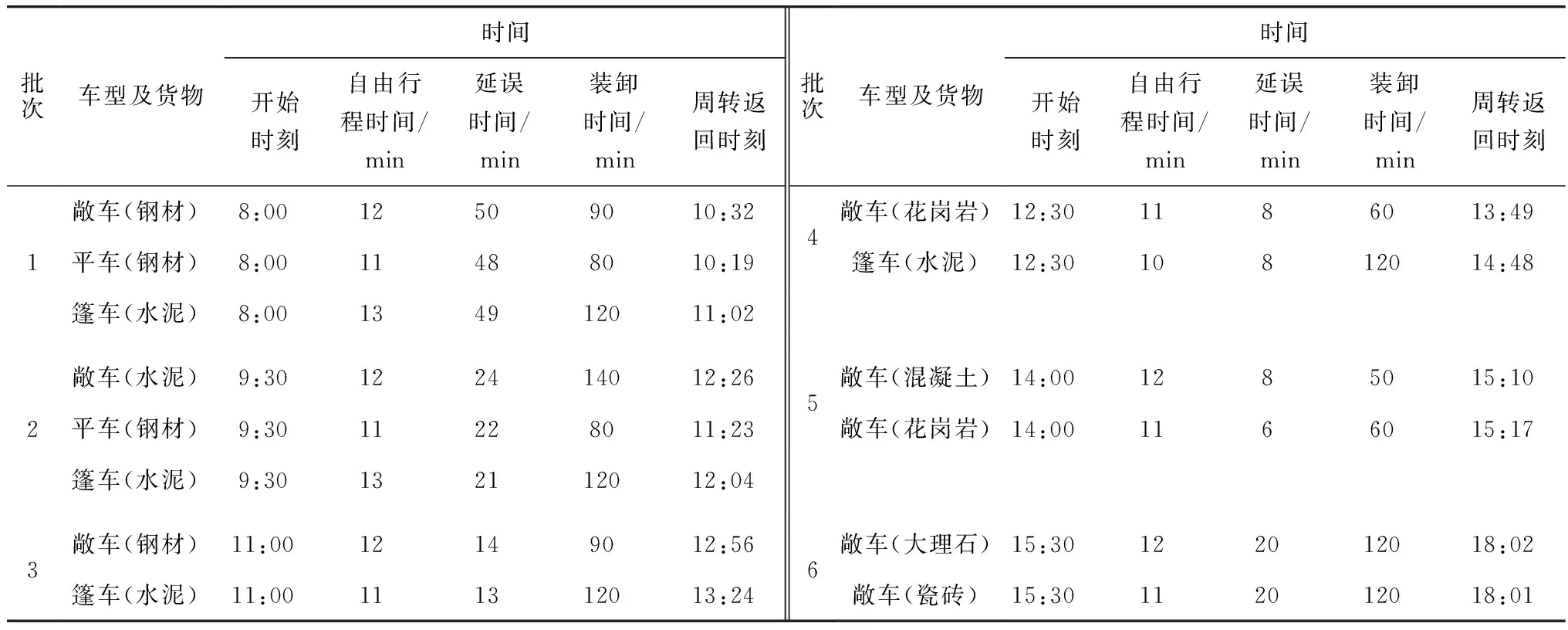
表2 車輛行程時間預測Table 2 Vehicle travel time prediction

4.2 結果分析

根據上述車貨以及車輛行程時間預測數據進行動態配載優化，用MATLAB軟件根據模型進行編程計算，每一階段優化結果如表3～表8。其中第1列剩余車數用“a+b-c+d”的形式來表示，a為貨運場站發車后的剩余車數，b為下一批任務開始前周轉返回的車輛，c為因故障需要保養維修的車輛數，d為之前保養維修后返回的車輛數，每種貨物所需的車輛數及運送噸數用“e/f”的形式來表示。

表3 第1批車貨配載優化Table 3 First batch vehicle-cargo stowage optimization

表4 第2批車貨配載優化Table 4 Second batch vehicle-cargo stowage optimization

表5 第3批車貨配載優化Table 5 Third batch vehicle-cargo stowage optimization

表6 第4批車貨配載優化Table 6 Fourth batch vehicle-cargo stowage optimization

表7 第5批車貨配載優化Table 7 Fifth batch vehicle-cargo stowage optimization

表8 第6批車貨配載優化Table 8 Sixth batch vehicle-cargo stowage optimization

在相同算例的情況下，用靜態解乘數法來對該問題進行求解，不考慮貨運場站車輛周轉返回以及車輛數在中途受到其他因素影響而改變，結果如表9。

表9 靜態解乘數法求解結果Table 9 The result of static solution multiplier method

將靜態配載與動態配載所需要的總車輛數進行比較，結果如表10。

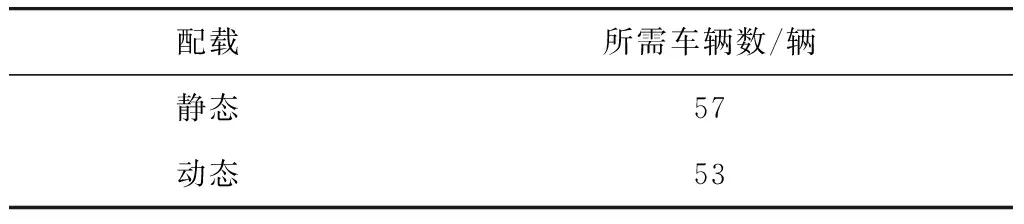
表10 靜態配載與動態配載所需要的總車輛數Table 10 Total number of vehicles required for static anddynamic stowage

從表10中可以看出，通過動態車貨配載優化后得出的結果更優，后者考慮到了運輸周轉返回的車輛對配載優化的影響，可以更好的應對車輛維修保養的情況，對于車貨的動態變化做出更為靈活的反應，同時減少貨車資源浪費，使得貨運場站可以將剩余的貨車資源投入到其他運輸任務中，提高場站的經濟效益。

5 結 語

對貨運場站貨車周轉的行程時間做了預測，使貨運場站能夠及時掌握貨車運輸周轉返回時間，進行相應的車輛調度和貨物裝運準備。針對公路貨運場站車貨的配載問題建立了數學模型，考慮到了周轉車輛返回后引起的車輛數變化，以及返回車輛可能進行維修保養暫時無法開展運輸任務而帶來的影響，通過動態解乘數法求解。算例結果表明該模型是有效的，可以更好地適應車輛與貨物的動態變化過程，節約貨車資源，合理優化貨車資源配置，進而為場站其它運輸任務提供便利，提高貨運場站的經濟效益和運作效率，為實際中的場站車貨配載提供理論參考依據和實際應用價值。