從“簡易方程”到“一元一次方程”
浦?jǐn)⒌?/p>

在七年級數(shù)學(xué)前三章中,我們分別學(xué)習(xí)了“第1章:數(shù)學(xué)與我們同行”“第2章:有理數(shù)”和“第3章:代數(shù)式”,現(xiàn)在我們開始學(xué)習(xí)“第4章:一元一次方程”。說到方程,大家并不陌生,因?yàn)樵谛W(xué)五年級我們就學(xué)習(xí)了“簡易方程”,知道了方程、方程的解與解方程等概念,并會利用方程解決簡單的實(shí)際問題。到了初中,“一元一次方程”與小學(xué)的“簡易方程”又有什么異同呢?
一、全面認(rèn)識研究方程的基本思路
首先,小學(xué)階段學(xué)習(xí)的方程、方程的解、解方程等概念以及用方程解決簡單的實(shí)際問題的思路同樣適用于一元一次方程;其次,一元一次方程是方程中最特殊、最簡單的方程。在初中階段,除了有特殊的一元一次方程之外,還有很多其他特殊的方程,它們都可以按照相同的思路和方法去研究。同學(xué)們可以從圖1來體會。
從圖1中我們可以看出,小學(xué)階段講的方程知識,正好是方程需要被研究的幾個(gè)方面,而研究一元一次方程,是規(guī)范、系統(tǒng)研究方程的開始。可見,本章內(nèi)容學(xué)得好與壞,直接影響后續(xù)方程的學(xué)習(xí)。因此,同學(xué)們一定要在初中方程的開始就學(xué)好、學(xué)深、學(xué)透,取得“良好的開端”,才可能達(dá)到“成功的一半”。
二、局部認(rèn)識研究方程的關(guān)鍵點(diǎn)
從數(shù)學(xué)知識的角度看,前面我們學(xué)習(xí)了數(shù)、式兩章內(nèi)容,因此,一元一次方程可以看成數(shù)與式的運(yùn)用;從生活實(shí)際的角度看,方程可以看成實(shí)際問題中含有未知量的相等關(guān)系抽象的結(jié)果。圖1告訴我們,從知識的角度看,要研究一元一次方程的定義、解、解法三個(gè)方面。下面,我們分別對這三個(gè)方面做一個(gè)研究。
方程的定義是“含有未知數(shù)的等式”;一元一次方程的定義是“只含有一個(gè)未知數(shù)(元),并且未知數(shù)的次數(shù)是1(次)”,由于涉及次數(shù),所以隱含了“方程中含有未知數(shù)的代數(shù)式是整式”。一元一次方程的解的定義跟方程的解的定義完全一樣,即“能使方程兩邊的值相等的未知數(shù)的值”。
我們再來看看等式與方程之間的聯(lián)系。
如“3+2=5”就是等式,而“3+x=5”就是方程。顯然,“x=2”就是這個(gè)方程的解。通過比較,我們可以看出,方程中的未知數(shù)看著不確定(未知),實(shí)際上是確定(已知)的,所以,方程的解也可以理解為“未知中的已知”。
求方程的解的過程叫作解方程。對于一元一次方程來說,分成“去分母→去括號→移項(xiàng)→合并同類項(xiàng)→系數(shù)化為1”五步,對于其中的每一步,我們都要明白變形的依據(jù)。
“去分母”是根據(jù)等式的性質(zhì),在方程的兩邊同時(shí)乘各分母的最小公倍數(shù),這是一個(gè)整體變形,要求每一項(xiàng)都乘到,這樣同學(xué)們就可以避免在解方程時(shí)犯“漏乘”的錯(cuò)誤;“去括號”是利用乘法分配律把括號去掉,這是一個(gè)局部變形,只涉及括號內(nèi)的每一項(xiàng);“移項(xiàng)”是根據(jù)等式的性質(zhì),在方程的兩邊同時(shí)加上(減去)某個(gè)項(xiàng),這是一個(gè)整體變形,要求方程的兩邊同時(shí)變形,從結(jié)果來看,只要把一些項(xiàng)“改變符號”后從方程的一邊移到另一邊即可;“合并同類項(xiàng)”是針對方程兩邊的同類項(xiàng)而言,這是一個(gè)局部變形,只要根據(jù)合并同類項(xiàng)法則進(jìn)行即可;“系數(shù)化為1”是根據(jù)等式的性質(zhì),在方程兩邊同時(shí)乘(除以)一個(gè)非0的數(shù),這是一個(gè)整體變形,要求方程兩邊同時(shí)進(jìn)行,結(jié)果把未知數(shù)的系數(shù)放到右邊已知數(shù)的分母上即可。
明確了一元一次方程的定義,我們就可以判斷一個(gè)方程是不是一元一次方程。反之,如果一個(gè)方程是一元一次方程,這說明它只含有一個(gè)未知數(shù),并且未知數(shù)的次數(shù)是1,進(jìn)而可以列出等式求出待定字母。明確了一元一次方程,我們可以通過解方程把它的解求出來,反之,知道一個(gè)方程的解,我們可以把它代入方程,求出待定系數(shù)。
三、整體認(rèn)識方程知識的模型價(jià)值
上面提到,方程可以看成解決實(shí)際問題中相等關(guān)系的一個(gè)模型,這就是本章最后一項(xiàng)內(nèi)容“用一元一次方程解決問題”。這個(gè)內(nèi)容可以說明兩點(diǎn):一是數(shù)學(xué)與生活是緊密相連的,數(shù)學(xué)來自生活實(shí)際;二是生活中的許多問題都可以用數(shù)學(xué)知識(方程)來解決,數(shù)學(xué)服務(wù)于生活實(shí)際。這充分體現(xiàn)了學(xué)習(xí)數(shù)學(xué)知識的價(jià)值。
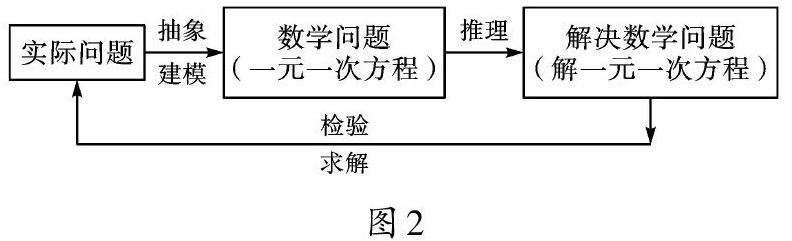
列方程解決實(shí)際問題的基本步驟可以概括為“設(shè)元→列出方程→解方程→檢驗(yàn)→作答”這五步。其中,設(shè)元后找到等量關(guān)系,把文字語言轉(zhuǎn)化為符號語言,進(jìn)而列出方程,是最關(guān)鍵的一步。從方程模型的整體角度看,就是“實(shí)際問題→抽象出數(shù)學(xué)問題(方程)→解決數(shù)學(xué)問題(解方程)→檢驗(yàn)并解決實(shí)際問題”(如圖2)。顯然,這個(gè)建立數(shù)學(xué)方程模型的過程,適合任何一個(gè)用一元一次方程解決的實(shí)際問題。
(作者單位:江蘇省無錫市新吳區(qū)教師發(fā)展中心)

