GCD封閉集上的冪矩陣行列式間的整除性
朱光艷, 李 懋, 譚千蓉
(1. 湖北民族大學教育學院, 恩施 445000;2.西南大學數學與統計學院, 重慶 400715;3.攀枝花學院數學與計算機學院, 攀枝花 617000)
1 Introduction
Throughout this paper, we denote by (x,y) (resp. [x,y]) the greatest common divisor (resp. least common multiple ) of integersxandy. LetZdenote the set of integers and |T| stand for the cardinality of a finitie setTof integers. Letfbe an arithmetical function andS={x1,…,xn}be a set ofndistinct positive integers. Let (f(xi,xj)) (abbreviated by (f(S))) denote then·nmatrix havingfevaluated at the greatest common divisor (xi,xj) ofxiandxjas its (i,j)-entry. Let (f[xi,xj])(abbreviated by(f[S])) denote then·nmatrix havingfevaluated at the least common multiple [xi,xj] ofxiandxjas its (i,j)-entry. Letξabe the arithmetical function defined byξa=xafor any positive integerx, whereais a positive integer. Then·nmatrix (ξa(xi,xj)) (abbreviated by (Sa)) and (ξb[xi,xj]) (abbreviated by [Sb]) are called power GCD matrix and power LCM matrix, respectively. A setSis calledfactorclosed(FC) if the conditionsx∈Sandd|ximply thatd∈S. We say that the setSisgcdclosedif (xi,xj)∈Sfor all 1≤i,j≤n. Evidently, any FC set is gcd closd but not conversely.
In 1875, Smith[1]showed that

whereμis the M?bius function andf*μis the Dirichlet convolution offandμ. Apostol[2]extended Smith’s result by showing that iffandgare arithmetical functions and ifβis defined for positive integerstandrby

then
det(β(i,j))=g(1)nf(1)…f(n).
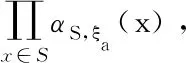
and
ES(x):={z∈Z+:?y∈S,y Divisibility is one of the most important topics in the field of Smith matrices. Bourque and Ligh[7]showed that ifSis FC, then (S)|[S] holds in the ringMn(Z) ofn×nmatrices over the integers. That is, there exists a matrixA∈Mn(Z) such that [S]=(S)Aor [S]=A(S). Hong[8]showed that such factorization is no longer true in general ifSis gcd closed. Letx,y∈Swithx Definition1.1[12]LetTbe a set ofndistinct positive integers and 1≤r≤n-1 be an integer. We say thatTis 0-fold gcd closed ifTis gcd-closed. We say thatTisr-foldgcdclosedif there is a divisor chainR?Twith |R|=rsuch that max(R)| min(TR)and the setTRis gcd closed. Note that Definition 1.1 is stated in a different way from that given in Ref.[12]. However, they are equivalent. It is easy to see that anr-fold gcd closed set is (r-1)-fold gcd closed, but the converse is not necessarily true. Hong[12]proved that the Bourque-Ligh conjecture is true whenn≤5 and ifn≥6 then the LCM matrix [S] defined on any (n-5)-fold gcd-closed setSis nonsingular. In 2005, Zhou and Hong[13]considered the divisibility among power GCD and power LCM matrices for unique factorization domains. On the other hand, Hong[14]initiated the study of the divisibility properties among power GCD matrices and among power LCM matrices. Tan and Lin[15]studied the divisibility of determinants of power GCD matrices and power LCM matrices on finitely many quasi-coprime divisor chains. In this paper, our main goal is to study the divisibility among the determinants of power matrices (Sa) and (Sb), among the determinants of power matrices [Sa]and [Sb] and among the determinants of power matrices (Sa) and [Sb]. The main result of this paper can be stated as follows. Theorem1.2Letaandbbe positive integers witha|band letn≥1 be an integer. (i) Ifn≤3, then for any gcd-closed setSofndistinct positive integers, one has det(Sa)|det(Sb), det[Sa]|det[Sb],det (Sa)|det [Sb]. (ii) Ifn≥4, then for any (n-3)-fold gcd-closed setSofndistinct positive integers, one has det(Sa)|det(Sb),det[Sa]|det[Sb]and det(Sa)|[Sb]. Evidently, Theorem 1.2 extends Hong’s theorem[16]obtained in 2003 and the theorems of Chen and Hong[17]gotten in 2020. Throughout this paper,aandbstand for positive integers. We always assume that the setS={x1,…,xn} satisfies thatx1<… In this section, we supply two lemmas that will be needed in the proof of Theorem 1.2. We begin with a result due to Hong which gives the determinant formulas of a power GCD matrix and a power LCM matrix on a gcd-closed set. Lemma2.1[18]LetS={x1,...,xn} be a gcd-closed set. Then and We can now use Hong’s formulae to deduce the formulae for det(Sa) and det[Sa] whenSis a divisor chain. Lemma2.2[17]LetS={x1,...,xn} be a divisor chain such thatx1|...|xnandn≥2. Then In this section, we use the lemmas presented in previous section to show Theorem 1.2. First, we prove part (i) as follows. Letn=1. It is clear that the statement is true. Letn=2. SinceS={x1,x2}is gcd closed, we have (x1,x2)=x1andx1|x2. It then follows that and The statement is true for this case. Letn=3. SinceS={x1,x2,x3} is gcd closed, we havex1|xi(i=2,3) and (x2,x3)=x1orx2. Consider the following two cases: Case 1 (x2,x3)=x1. Then and The statement is true for this case. Case 2 (x2,x3)=x2. Thenx2|x3. It follows that and The statement is true for this case. Part (i) is proved. Consequently, we prove part (ii).First of all, any (n-3)-fold gcd-closed setSmust satisfy eitherx1|x2|…|xn-3|xn-2|xn-1|xn, orx1|x2|…|xn-3|xn-2and gcd(xn,xn-1)=xn-2. Case aSis a divisor chain. That is,x1|x2|…|xn-3|xn-2|xn-1|xn. Then by Lemma 2.2, one deduces that and The statement is true for this case. Case bx1|x2|…|xn-3|xn-2and gcd(xn,xn-1)=xn-2. By Lemma 2.1, one has and Then and The statement is true for this case. Finally, we prove part (iii).Letn≥4 be an integer,a=1,b=2 and xk=3k-1,1≤k≤n-3, xn-2=2·3n-4,xn-1=7·3n-4,xn=28·3n-4. By Definition 1.1, one knows thatSis (n-4)-fold gcd closed. By Lemma 2.1, one has det(Sb)=61·23n-6·3n2-3n-1, and det[Sb]=(-1)n-4·191·74· 23n-2·3n2-n-9. Then we can compute and obtain that and Part (iii) is proved. This finishes the proof of Theorem 1.2.
2 Auxiliary results
3 Proof of Theorem 1.2


