2021年新課標Ⅲ卷解析幾何試題賞析與探究

潘 宇

(廣東省華南師大附中汕尾學校 516600)

2021年高考剛剛落下帷幕，全國各地老師紛紛對其中的優秀試題展開研究.筆者在研究2021年新課標Ⅲ卷第20題解析幾何時，發現該題既可以用特殊位置猜想結果，又可以用基本思想方法解答.此題不僅可以尋找到往年舊題中的縮影，更能挖掘其深藏的競賽背景，下面筆者以此題為例，從真題解法賞析、試題背景探源、基本思想方法的應用和教學啟示等四個方面展開詳細闡述.

一、真題解法賞析

例1 (2021年新課標Ⅲ卷第20題)拋物線C的頂點為坐標原點O，焦點在x軸上，直線l:x=1交C于P，Q兩點，且OP⊥OQ，點M(2，0)，且⊙M與l相切.

(1)求C，⊙M的方程；

(2)設A1，A2，A3是C上的三個點，直線A1A2，A1A3均與⊙M相切，判斷直線A2A3與⊙M的位置關系，并說明理由.

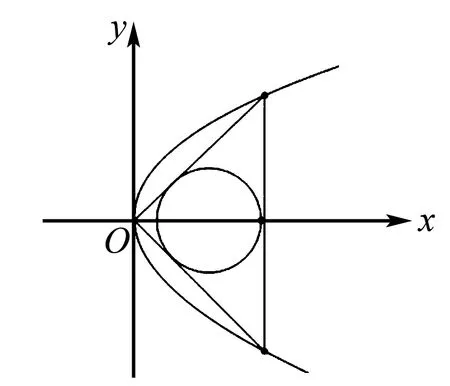
圖1

評注由于第二問難度較大，很多學生可能想不到如何破解或者在考場上來不及研究，所以可以先用“特殊化”的思想，預測答案，再從“特殊到一般”，尋找證明思路，或者書寫有效的得分步驟，爭取得分最大化.

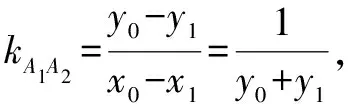
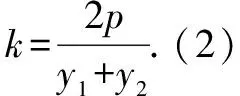
二、試題背景探源

例1的競賽背景為彭賽列閉合定理：平面上給定兩條圓錐曲線，若存在一封閉多邊形外切其中一條圓錐曲線且內接另一條圓錐曲線，則此封閉多邊形內接的圓錐曲線上每一個點都是滿足這樣(切、內外接)性質的封閉多邊形的頂點，且所有滿足此性質的封閉多邊形的邊數相同.

簡明的彭賽列閉合定理表示為：一個三角形外接于一個圓，內切一個圓，則三角形的外接圓可以有無數個內接三角形滿足其內切圓為上述的同一個.于是可以得到例1分析如下：

評注知道彭賽列閉合定理可以幫助我們預判解題之路，但缺點是這些超綱知識不可用于考場答卷.所以幫助我們解決圓錐曲線的內接三角形的內切圓問題的最重要方法還是通性通法，也就是前文分析2后的總結(1)、(2)、(3).下面繼續舉例說明這些總結的應用.

三、基本思想方法的應用

例2 (2021年全國八省聯考第7題)已知拋物線y2=2px上三點A(2,2),B,C，直線AB,AC是圓(x-2)2+y2=1的兩條切線，則直線BC的方程為( ).

A.x+2y+1=0 B.3x+6y+4=0

C.2x+6y+3=0 D.x+3y+2=0

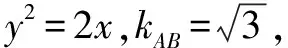
評注以上的例1、例2都是考查拋物線的內接三角形的內切圓問題，下面看看一個橢圓中的例子.研究往年經典題可以提煉解題方法，指導未來解題.

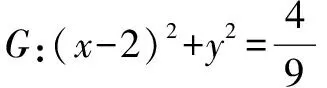
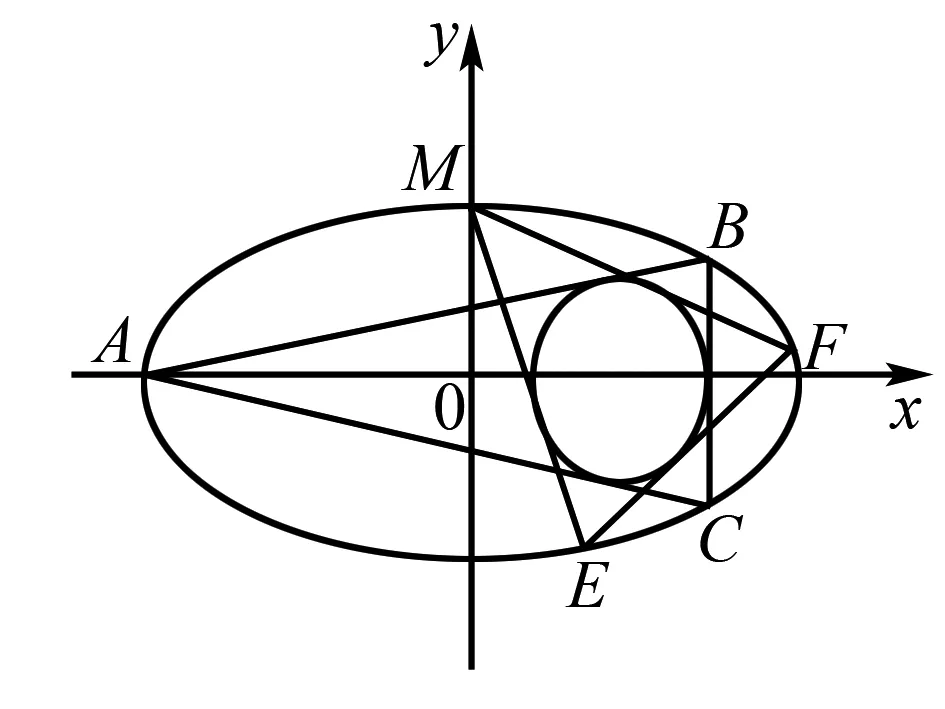
圖2

評注該題是典型的彭賽列閉合.積極研究往年經典例題，并用于日常教學，不僅可以“與命題者對話”，在研究掌握通性通法的同時訓練學生的計算毅力，還可以滲透數學文化、括展知識面，往前追溯，還可以在聯賽試題中找到類似考法.

例4 (2008高中數學聯賽)點P是拋物線y2=2x上的動點，點B,C在y軸上，圓(x-1)2+y2=1內切于ΔPBC，求ΔPBC面積的最小值.

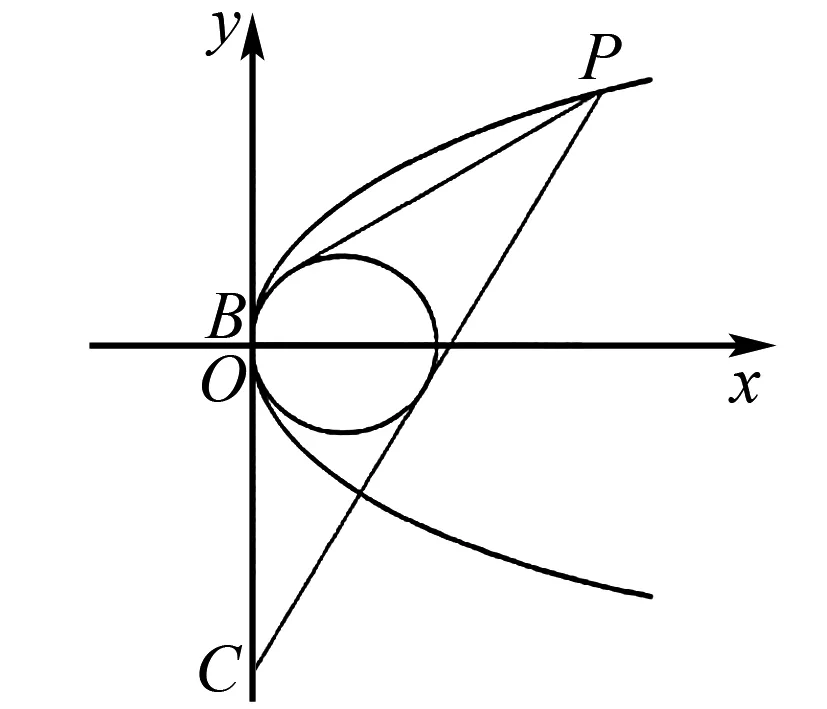
圖3

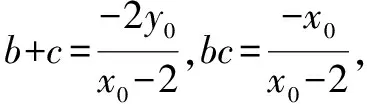
點評從以上例題的解答過程可以提煉出解析幾何最常用的解題思想方法：設點、設線、聯立、消元、設而不求，仍然是圓錐曲線解題的主旋律；以點斜式、點線距離公式、線圓相切等知識為載體，通過運算求解、方程變形，得到“同構”二次方程，再結合根與系數的關系找到解題突破口.

四、教學啟示

隨著新課程、新教材、新高考的逐步推進，圍繞數學學科核心素養落實的全國卷數學試題已然引領著新時期的數學教學改革.基于2021年新課標Ⅲ卷數學第21題解析幾何試題的全面闡述，在解析幾何教學中需要關注的的幾個方面有：

1.貫徹解析幾何基本思想方法，回歸數學本質.解析幾何其核心思想就是運用代數的方法研究幾何問題，故而其關鍵要處理的是幾何問題.因此在解析幾何實踐教學中要注重幾何關系的分析，厘清復雜曲線中的幾何關系，尤其是直線與曲線的常見位置關系(相切、平行、垂直)的代數等價形式，其基本處理方法是“設而不求”和“設且求”.

2.滲透類比探究思想，強化思維訓練，提升運算素養.解析幾何內容，尤其是有心二次曲線的性質常常都具有極其類似的結論，因而在引導學生進行自主探究活動中始終樹立類比推理的意識，充分挖掘出與已知知識相鄰的“知識圈”.在探究推理過程中遵循特殊到一般原則，狠抓學生數學運算能力的培養，培養學習數學的自信心和創新思維.

3.關注學科知識間的融合，培養發現問題和解決問題的能力.2021年新課標Ⅲ卷數學第21題第(2)問考查學生在開放的情境中發現主要矛盾的能力，結合特殊值的思想與彭賽列閉合定理理論支撐，能夠明晰問題結論，指引推理方向.因此在解析幾何的教學中需要適當關注數學文化，融合不等式、導數等學科知識.

解析幾何問題，不僅僅是運算問題，更是思維問題.“多考一點想，少考一點算”新高考理念下的解析幾何問題，設問開放，教學的核心始終圍繞基本思想方法才是解決問題的關鍵.