多視角解析一道2021年三模壓軸題
賀鳳梅
(新疆伊犁鞏留縣高級中學 835400)
一、題目呈現
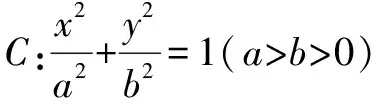
(1)求橢圓C的標準方程;
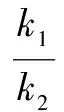
二、總體分析
定點、定值是圓錐曲線中的常見問題,問題的呈現形式有:以兩直線斜率乘積、和、比值為定值引出的直線過定點;或已知直線過定點,能否得出兩直線斜率之積、和或比值為定值.本文擬以直線過定點,兩直線斜率比值為定值進行多視角探究,旨在理清問題的本質,找到解決此類問題的行之有效的方法.
三、試題解答
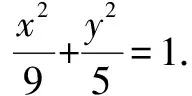
以下重點探討第(2)問.
視角1利用直線的普通方程求解.
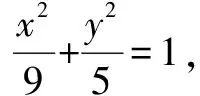
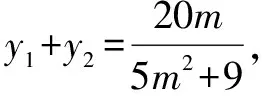
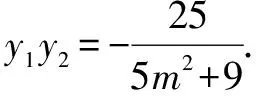
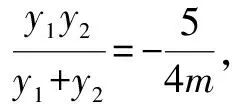
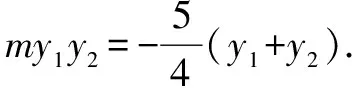
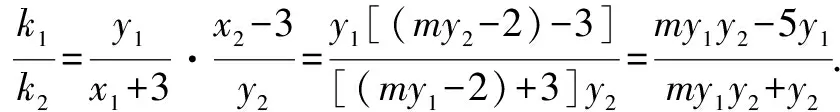
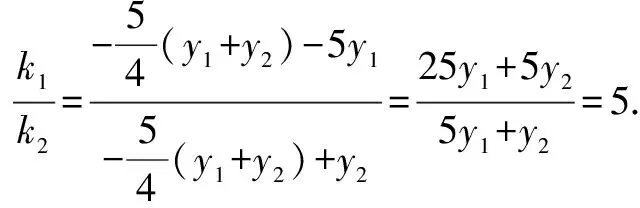
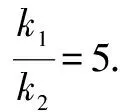
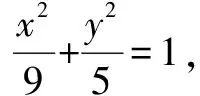

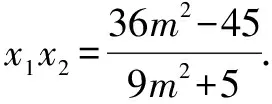
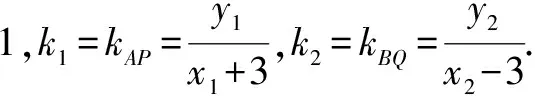
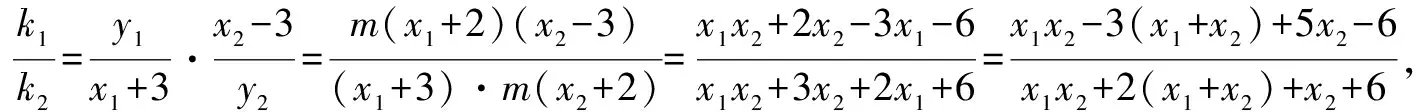
將④⑤代入,化簡整理,得
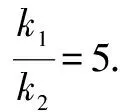
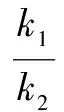
視角2圓錐曲線齊次化,借助橢圓的第三定義求解.
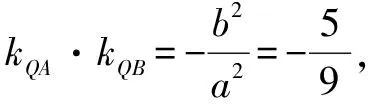
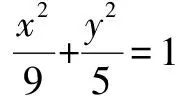
又直線m(x+3)+ny=1過點F(-2,0),所以m=1.
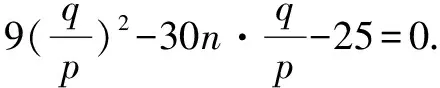
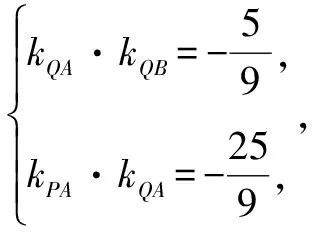
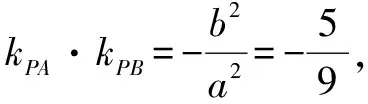
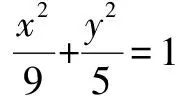
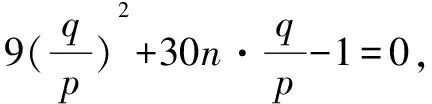
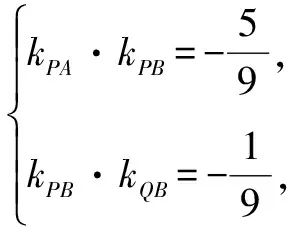
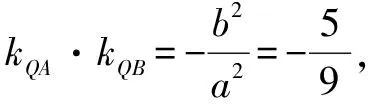
此時,直線方程設為mp+nq=1.⑦
直線過點(1,0),所以m=1.
將⑦代入⑥,得9y2-30nxy-25x2=0,
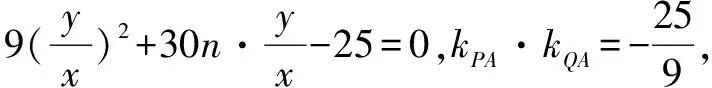
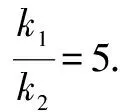
評注以上三種解法的本質是圓錐曲線的齊次化,其中一種策略是平移圓錐曲線,比如以上的解法5,不過學生對這種方法有些陌生.筆者將方法稍微改變一下,步驟為:
(1)設直線方程為m(x-x0)+n(y-y0)=1;
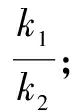
(4)得出結論:比如以上的解法3和解法4.當然還需要借助橢圓的第三定義聯合求解.
視角3借助韋達定理求解.
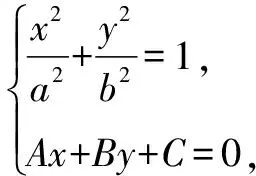
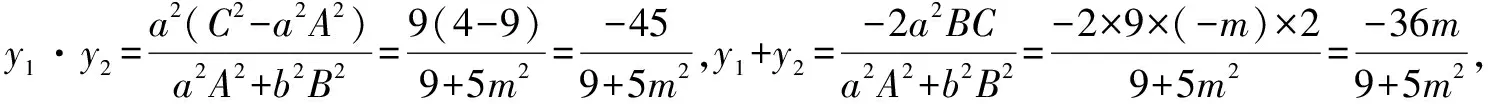

評注圓錐曲線結合韋達定理,求解的方法又稱圓錐曲線的公式聯立,其實是一套求解橢圓(或雙曲線)與直線相交時,聯立方程求判別式、韋達定理與相交弦等問題的公式,平時并不多見.針對學有余力的學生,教師可以適當介紹,開闊學生的視野,提高學生的思維能力.
四、解后反思
《普通高中數學課程標準(2017)》指出,高中數學的六大素養為數據分析、邏輯推理、數學抽象、數學建模、直觀想象、數學運算.高中數學的學習急需提高學生的綜合能力.在數學學習的過程中,教師要鼓勵和引導學生在學習的過程中勤思考、多動腦,在對兩直線斜率比值、乘積以及和為定值的問題探究過程中,培養學生數學運算、邏輯推理、直觀想象的核心素養.教師可以根據核心素養所提出的相關理論進行教學方式、教學目的的調整,使學生能夠得到更全面的發展,將立德樹人的根本任務落到實處.
“一題多解”既可以豐富教學內容,也可以讓枯燥的數學課堂變得活潑生動,充分調動學生的積極性,讓每個學生都自覺地投入到課堂中來,不僅可以使學生集中注意力,還可以使學生的思維越來越縝密,考慮越來越周全.應用“多題一解”的教學,可以鍛煉學生歸納總結的能力,使得學生“做一題,會一類”.“多題一解”的數學教學方式,不僅能提高學生學習數學的能力,還能映射生活的哲理,對于學生生存能力的提高也有效果.

