自相關倒譜擴頻信號擴頻周期估計算法*

李 星，張利強，盛 興，袁宗圃，孫 吉

（光電對抗測試評估重點實驗室，河南 洛陽 410073）

0 引言

直接序列擴展頻譜（Direct Sequence Spread Spectrum，DSSS）通信技術簡稱直擴通信技術，其具有低信噪比、強抗干擾以及強隱蔽性等優點。擴頻通信不僅應用于軍事通信和信息網絡對抗等領域，還廣泛應用于雷達、定位系統以及衛星導航等民用領域。由于非合作條件下擴頻通信系統的偵察和干擾均在較大難題，因此研究針對擴頻通信通信系統的對抗技術尤為重要。

本文針對擴頻信號偽碼周期估計技術開展研究工作，分析直擴信號的基本特征和直擴信號擴頻周期估計的常用算法，并就倒譜算法進行深入研究。針對常規倒譜算法存在的不足，對傳統倒譜法進行了3 點改進：（1）引進窄窗口自相關，強化了直擴信號周期特性，降低了擴頻周期估計起效信噪比；（2）優化了周期峰值的搜索策略；（3）利用峰值漏檢情況下的多個峰值數據，進一步提高了估計算法的準確度。仿真結果表明，本文提出算法峰值更加突出，更利于周期峰值搜索，且能夠在低信噪比情況下從虛假峰值中分揀出正確的數據，同時在峰值漏檢的情況下能夠更好地利用峰值數據高效檢測直擴信號偽碼周期。

1 自相關倒譜

直擴信號定義為：

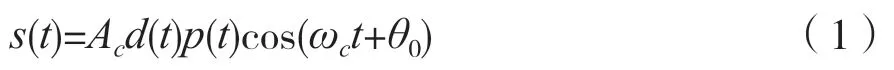
式中：d(t)為調制信息碼；p(t)為偽隨機序列；ωc和θ0分別為載波頻率和初相。擴頻過程是每一個調制信息碼片與偽隨機序列相乘，因此直擴信號存在兩重周期性，第一重周期為調制序列，第二重周期為擴頻序列。本文重點考慮第一種，即直擴信號的偽碼周期長度。

倒譜定義為信號的對數功率譜的功率譜[1]，能夠很好地反映信號的時域周期性，廣泛應用于地震回波信號、生物醫學信號及聲吶信號的周期檢測，也在直擴信號偽碼周期估計中得到了應用[2-4]。但是，當信號信噪比較低時，信號的周期性特性被弱化，此時倒譜算法的性能將劇烈惡化。BUREL 論證了直擴信號的自相關函數與噪聲的自相關函數之間的差別，提出利用自相關函數的二階矩檢驗DSSS 信號，取得了較好的效果[5]。該算法直接對直擴信號的基帶信號求取自相關，只是對噪聲進行平滑，無法利用擴頻序列的周期性即強相關性。考慮到直擴信號信噪比較低，在進行參數估計時需要多周期數據累計，需要的采樣信號較長，此時直接對信號求取時域自相關計算量較大。因此，本文考慮從截獲信號中選取一段信號對整個信號作時域相關，在強化擴頻碼周期性的同時利用了擴頻序列的周期重復特性，表達式為：

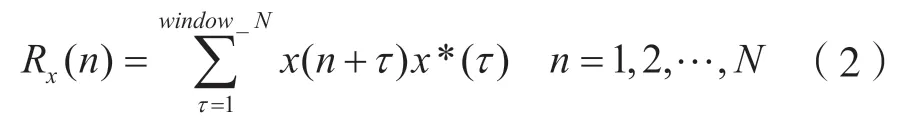
式中：window_N為選取信號長度，也稱為窗口長度；N為時域信號長度。由于擴頻信號擴頻碼有很強的自相關特性，因此信號的自相關會周期性地出現峰值，峰值之間的距離為擴頻碼周期長度，如圖1 所示。

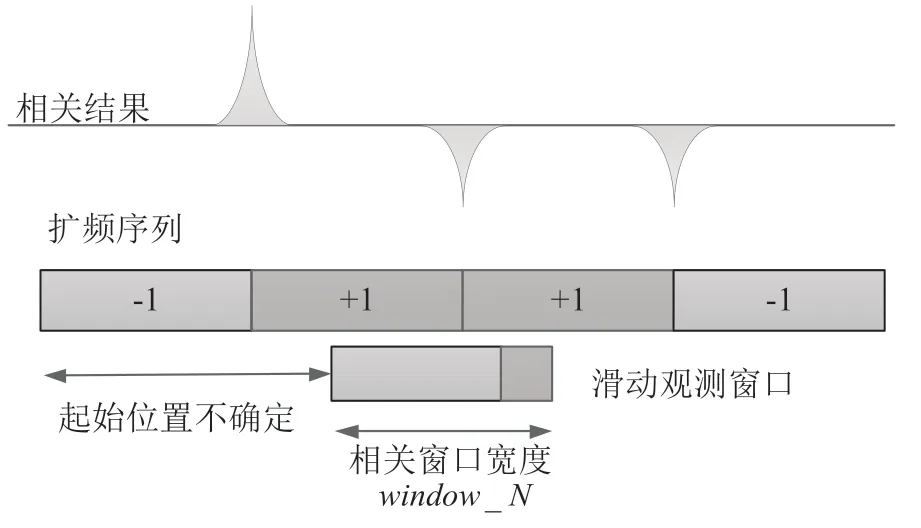
圖1 直擴信號延時相關結果

由于事先無法獲取擴頻信號的同步信息，因此窗口的起始位置是隨機選取的。當用于相關的窄窗口數據橫跨兩個擴頻符號時，兩個擴頻符號的反向會抵消部分峰值數據；當相關窗口小于擴頻周期長度時，這種情況的出現概率會極大降低，相關峰值更多。

生成一段直擴信號，擴頻碼長為31，碼速率為1 Msps，采樣率為16 Msps，FFT 點數為16 384，信噪比為10 dB，信號的擴頻周期長度為31×16=496。分別設置觀測窗口長度為297（擴頻周期0.6 倍）、793（擴頻周期1.6 倍），信號的自相關結果如圖2和圖3 所示。

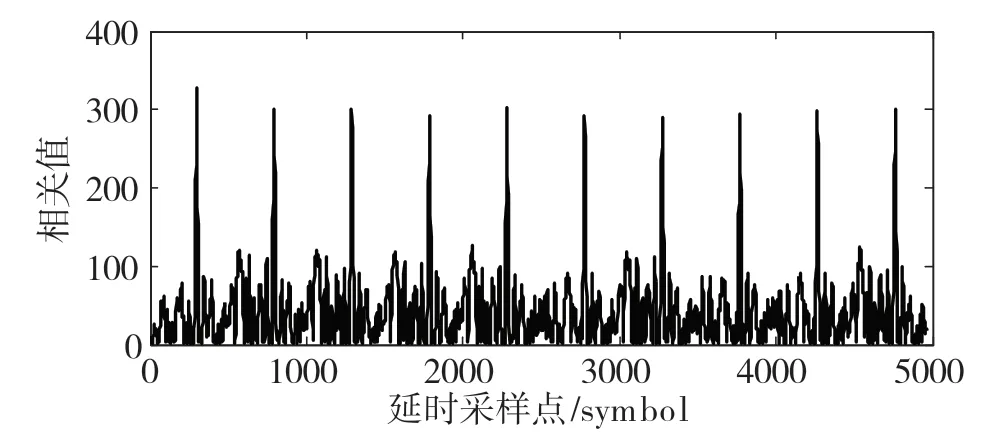
圖2 直擴信號延時相關

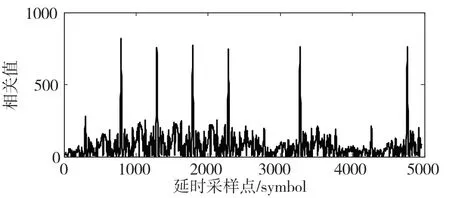
圖3 直擴信號延時相關

從圖2 和圖3 可以看出，由于擴頻碼的強相關性，導致信號的自相關周期性出現相關峰，且峰值隨著調制序列的幅度而改變。觀測窗口大于和小于擴頻周期長度均會出現周期性峰值，且峰值的距離為擴頻周期長度。

利用窄窗口對擴頻信號進行自相關處理，相關峰能夠反映擴頻信號的擴頻周期特性。因此，利用自相關結果進行倒譜運算，較直接使用倒譜運算峰值更加明顯，計算公式為：

為了比較常規倒譜與時域自相關倒譜的結果，生成一段直擴信號，擴頻碼長為31，碼速率為1 Msps，采樣率為16 Msps，FFT 點數為16 384，信噪比為-10 dB。設置觀測窗口長度為800，分別計算信號的倒譜與信號的自相關倒譜，平均次數30，結果如圖4 和圖5 所示。

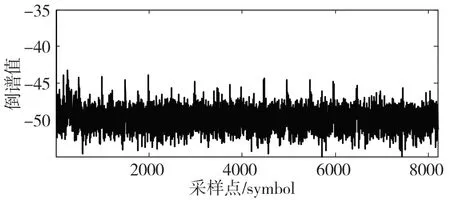
圖4 擴頻信號倒譜

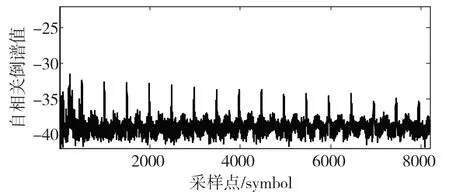
圖5 擴頻信號自相關延時倒譜

對比圖4 和圖5 可以看出，在相同的信噪比與平均次數條件下，直擴信號自相關倒譜的峰值特性更加明顯，能夠在更低的信噪比條件下有效估計直擴信號的擴頻周期。

2 最小二乘自相關倒譜擴頻周期估計算法

2.1 問題的提出

估計直擴信號的偽碼周期時需要面臨以下2 個問題：

（1）直擴信號信噪比較低，不同的算法利用擴頻碼周期重復的特性，使用峰值來提取偽碼周期[1-6]，但在低信噪比情況下難以提取有效的峰值，導致估計結果偏差較大；

（2）從圖4 可以看出，在進行峰值提取時，峰值幅度受到噪聲的影響出現較大波動，導致出現低幅度峰值漏檢的情況。

針對以上存在的問題，本文提出一種基于時域自相關倒譜的直擴信號偽碼周期估計算法，利用時域自相關特征進一步降低噪聲對信號的影響，并使用峰值檢測策略提取周期出現的峰值，最后使用最小二乘擬合思想最大化地利用峰值漏檢情況下的峰值數據，實現了對直擴信號偽碼周期的高性能估計。

2.2 峰值檢測

在處理受噪聲干擾的信號時，需要考慮倒譜峰值的虛警和漏檢。因此按照如下方法近似峰值搜索。

（1）檢測倒譜的峰值位置，并進行逐次作差：

（2）提取周期出現的峰值間隔

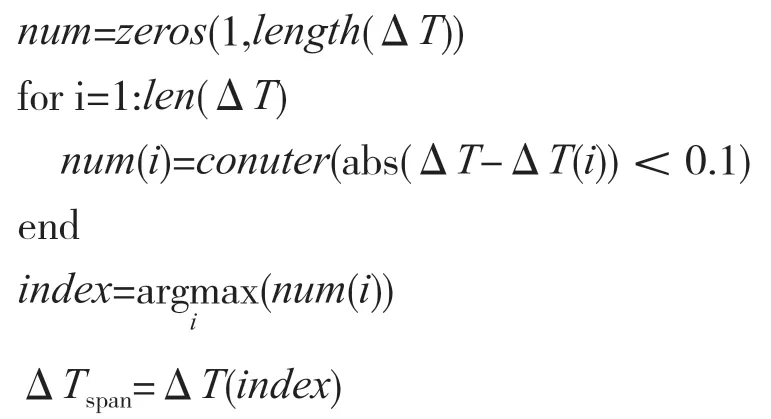
其中：conuter()為計數函數。

（3）分揀出ΔT中與ΔTspan接近的數據，組成單倍峰值間隔矩陣：

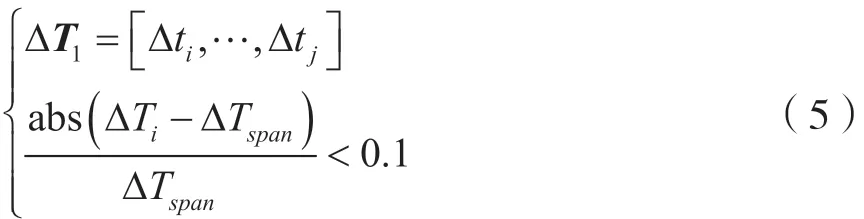
步驟（2）為從峰值間隔矩陣ΔT中提取出現次數最多的峰值間隔作為ΔTspan，為單倍峰值間隔。步驟（3）～步驟（5）為提取2 倍和3 倍峰值間隔，考慮了峰值漏檢1 次和2 次的情況。

2.3 峰值漏檢情況下的數據擬合

使用最小二乘方法對多個觀測數據下的結果進行擬合[7]，求取最佳的周期值。

不同倍數m的擴頻周期下倒譜峰值距離y可以寫成：

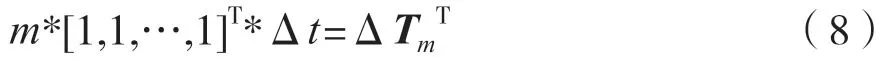
將式（8）整理為矩陣形式：

利用最小二乘公式[8]得到擴頻周期：

式中：(MTM)-1MT為矩陣M的偽逆。利用最小二乘可以綜合利用多組包含漏檢的峰值數據，得出最小均方誤差情況下的擴頻周期估計結果。

2.4 自相關倒譜倒譜擴頻周期估計算法

倒譜相鄰峰之間的間隔是偽碼周期Tc。當信噪比很低時，很有可能某個或某幾個相關峰值在噪底之下。因此，算法要檢測所有可能的峰值，從多個峰值間隔中計算當前直擴信號的擴頻周期。基于自相關倒譜法直擴信號擴頻周期估計算法如下。

輸入：直擴信號s1，觀測窗口window_n，輸出擴頻信號擴頻周期Tc。

（1）取出一段長度為signal_len的信號s1，設置觀測窗口長度window_n，在信號中取出一段長度為window_n的信號s2；

（2）計算信號的延時相關值，即：

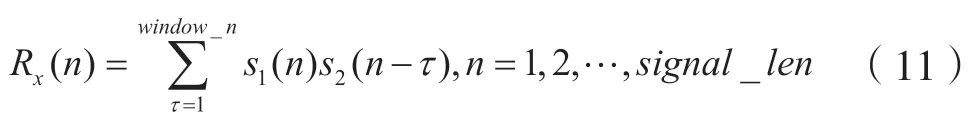
（3）計算延時相關信號的倒譜；

（4）將倒譜C中前window_n個值丟棄；

（5）尋找C所有的相關峰；

（6）對步驟（5）中獲取的峰值位置做差分，求出相鄰相關峰之間的位置ΔT=[Δt1,Δt2,…,Δtm]；

（7）利用峰值檢測策略求取矩陣M和ΔT'。

（8）利用式（10）求取偽碼周期。

算法的步驟（7）是為了剔除假峰值引起的錯誤峰值間隔，如果一個峰值間隔的兩個峰值都是正確的，那么該間隔會在結果中反復出現，且次數最多。步驟（8）是為了防止峰值漏檢，在出現漏檢時前后兩個峰值的距離將會是擴頻周期的整數倍。

3 算法仿真

為了驗證算法的有效性，生成一段直擴信號，擴頻碼長為31，碼速率為1 Msps，采樣率為16 Msps，FFT 點數為16 384，觀測窗口800，使用本文算法進行峰值檢測，直方圖統計結果如圖6 所示。

圖6 峰值間隔次數統計結果

從圖6 可以看出，經過多次峰值間隔累計，峰值間隔在真實擴頻周期長度496 處出現次數很多，同時受噪聲的影響，出現了較多的虛警和漏檢，部分峰值間隔出現在兩倍擴頻周期長度992 處。峰值間隔較小的虛假峰值通過本文的算法排除這部分數據，將在算法的步驟（7）中得到很好的利用。

分別使用傳統倒譜算法和本文提出的算法對生成的擴頻通信信號進行擴頻周期估計，統計不同信噪比下擴頻碼周期估計誤差，結果如圖7 所示。

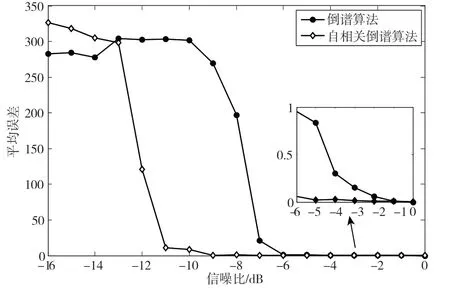
圖7 不同信噪比條件下擴頻周期估計誤差

從圖7 可以看出，本文所提算法較常規倒譜算法在性能方面有明顯提升，算法起效性信噪比更低。由于使用了漏檢情況下的峰值間隔數據，本文算法在信噪比條件下較常規倒譜算法依舊有更高的準確度（在仿真試驗中信噪比低于-13 dB 時，兩種算法倒譜的峰值均由噪聲引起，估計結果沒有比較的意義）。

4 結語

本文對直擴信號的擴頻周期估計開展研究，針對傳統算法在低信噪比條件下算法性能不佳和峰值搜索中存在漏檢的問題進行改進，研究了基于窄窗口自相關倒譜和峰值漏檢條件下擴頻周期最小二乘擬合相結合的直擴通信信號擴頻周期估計算法。本文提出的算法復雜度較低，起效信噪比較低，具有較強的工程應用價值，還可以為其他峰值提取算法提供新思路。