重復(fù)使用運(yùn)載器著陸滑跑距離估算方法研究

朱如意，王 征，張春陽(yáng)，張?jiān)铝?/p>

（中國(guó)運(yùn)載火箭技術(shù)研究院，北京，100076）

0 引 言

重復(fù)使用運(yùn)載器在再入返回著陸后要經(jīng)歷地面滑跑段直至停機(jī)。地面滑跑段是飛行任務(wù)剖面重要的組成部分。對(duì)于重復(fù)使用運(yùn)載器而言，其再入返回著陸時(shí)滑跑距離的長(zhǎng)短不僅反映飛行器的性能水平，同時(shí)也影響其他一些因素，比如著陸場(chǎng)選擇或設(shè)計(jì)、是否使用減速傘、控制系統(tǒng)設(shè)計(jì)、起落架系統(tǒng)設(shè)計(jì)等。著陸場(chǎng)跑道的高度會(huì)影響滑跑距離的長(zhǎng)短，在其他條件不變情況下，著陸場(chǎng)跑道高度越高、著陸速度越大，滑跑距離越長(zhǎng)；著陸場(chǎng)跑道高度越低、著陸速度越小，滑跑距離越短，對(duì)起落架輪胎的使用壽命越有利，對(duì)于可重復(fù)使用的飛行器而言是利好因素。地面滑跑距離是飛行器著陸性能中最主要的指標(biāo)之一，良好的著陸性能對(duì)飛行器的安全著陸至關(guān)重要。為了滿足滑跑距離的要求，需要研究是否使用減速傘以縮短滑跑距離，是否優(yōu)化起落架剎車裝置，是否優(yōu)化控制系統(tǒng)設(shè)計(jì)，這些因素相關(guān)聯(lián)，進(jìn)而影響的是飛行器總體設(shè)計(jì)。

目前，滑跑距離的計(jì)算或者分析諸多見于飛機(jī)，涵蓋飛機(jī)起飛滑跑距離和跑道長(zhǎng)度、發(fā)動(dòng)機(jī)推力計(jì)算等，鄧楊晨等[1]通過(guò)優(yōu)化方式給出了發(fā)動(dòng)機(jī)的最佳安裝角和飛機(jī)地面滑跑的最佳攻角及前起落架的最佳凸伸量，并確定了飛機(jī)地面滑行過(guò)程中的最短滑跑距離；宋花玉等[2]應(yīng)用人工神經(jīng)網(wǎng)絡(luò)技術(shù)對(duì)飛機(jī)起飛滑跑距離進(jìn)行了研究，給出了基于BP網(wǎng)絡(luò)的飛機(jī)起飛滑跑距離計(jì)算模型，并對(duì)飛機(jī)實(shí)際滑跑距離及其影響因素進(jìn)行了歸一化處理；張志剛等[3]針對(duì)MA60飛機(jī)進(jìn)行了高原機(jī)場(chǎng)起飛性能研究，結(jié)合MA60飛機(jī)的特性，計(jì)算出起飛滑跑距離等參數(shù)值；在發(fā)動(dòng)機(jī)推力計(jì)算和滑跑長(zhǎng)度計(jì)算方面，宋花玉[4]利用數(shù)值理論計(jì)算了飛機(jī)起飛滑跑距離，研究了發(fā)動(dòng)機(jī)瞬時(shí)推力的確定方法，提出以發(fā)動(dòng)機(jī)推力曲線為基礎(chǔ)，通過(guò)拉格朗日插值確定未知推力的算法；黃文靜等[5]針對(duì)裝有反推力裝置的某型飛機(jī)，給出了著陸滑跑距離向標(biāo)準(zhǔn)條件換算的方法。許震宇等提出了地效飛行器或水上飛機(jī)水面起飛滑跑距離估算方法，在基本運(yùn)動(dòng)方程中引入了機(jī)身浸濕面積與滑行速度成負(fù)斜率線性關(guān)系的假設(shè)，簡(jiǎn)化起飛距離的計(jì)算過(guò)程，得到發(fā)動(dòng)機(jī)推力與起飛滑行距離之間的關(guān)系曲線[6]。航天飛機(jī)不同架次著陸滑跑距離統(tǒng)計(jì)數(shù)據(jù)可見公開文獻(xiàn)[7]，但未涉及滑跑距離計(jì)算方法。對(duì)重復(fù)使用運(yùn)載器、無(wú)動(dòng)力再入飛行器滑跑段模型研究還比較少，對(duì)滑跑距離方法研究也比較少。

重復(fù)使用運(yùn)載器再入及滑跑段無(wú)動(dòng)力，受氣動(dòng)力、風(fēng)、減速傘一系列因素影響，單純應(yīng)用飛機(jī)著陸的經(jīng)驗(yàn)公式，不足以準(zhǔn)確估算飛行器滑跑距離。本文提出一種簡(jiǎn)單易懂的滑跑距離估算方法，在跑道坐標(biāo)系下建立飛行器著陸滑跑估算模型，考慮減速傘和地面風(fēng)影響，研究不同滑跑工況下的滑跑距離估算方法。該滑跑距離估算方法簡(jiǎn)潔、算法易實(shí)現(xiàn)，適合工程應(yīng)用。

1 滑跑距離估算模型

可重復(fù)使用運(yùn)載器地面滑跑時(shí)的實(shí)際運(yùn)動(dòng)是一種復(fù)雜的現(xiàn)象，為了使計(jì)算盡量簡(jiǎn)單而不失準(zhǔn)確性，需要進(jìn)行簡(jiǎn)化假設(shè)。在建立著陸滑跑估算模型時(shí)與絕大部分模型一樣，將飛行器視為理想剛體，忽略機(jī)體彈性振動(dòng)的影響。

因?yàn)楸疚牡幕芫嚯x估算采用簡(jiǎn)化算法，是沿著跑道方向開展滑跑距離估算，故選擇在跑道坐標(biāo)系下建立著陸滑跑估算模型，著陸場(chǎng)跑道坐標(biāo)系OdXdYdZd見圖1。飛行器著陸滑跑時(shí)飛行器受力狀態(tài)如圖2所示。

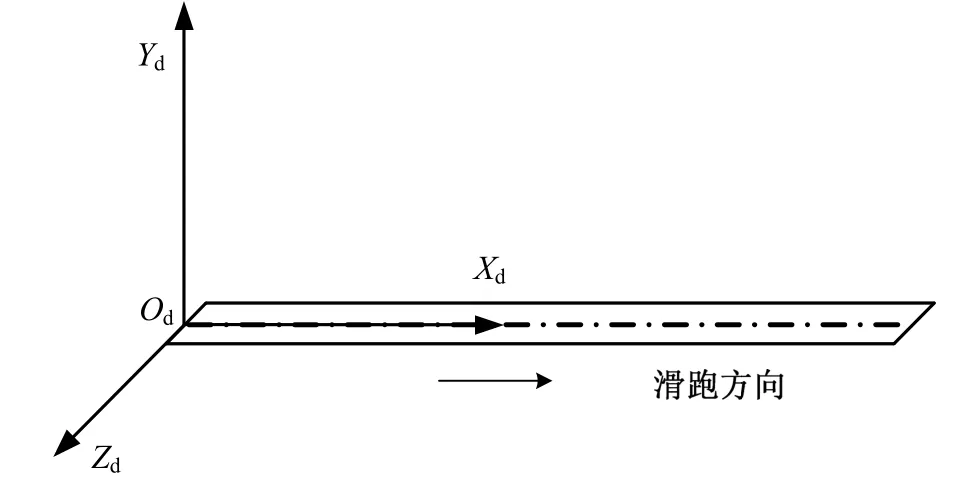
圖1 著陸場(chǎng)跑道坐標(biāo)系Fig.1 The Runway Reference Frame

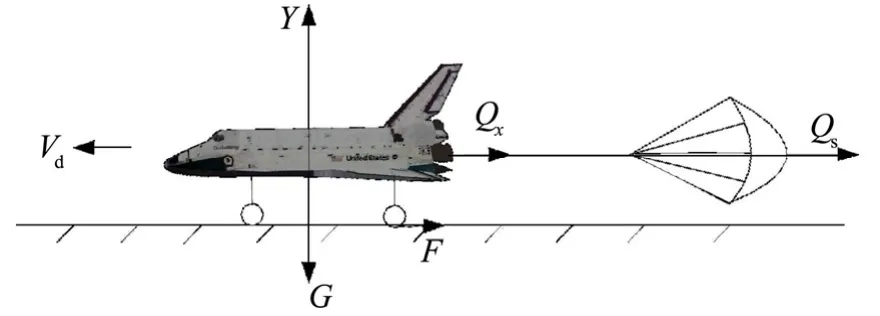
圖2 飛行器受力狀態(tài)Fig.2 The Force State of the Aircraft

減速傘張滿后飛行器著陸滑跑運(yùn)動(dòng)方程為

式中m為飛行器總質(zhì)量；Vd為地速；Qx為氣動(dòng)阻力；Qs為阻力傘拉力；F為地面作用在飛行器上的摩擦力和剎車阻力。

考慮地面風(fēng)的影響，有：

式中Cx，Cy為滑跑時(shí)氣動(dòng)阻力、氣動(dòng)升力系數(shù)；CsAs為減速傘特征值；u0為滾動(dòng)摩擦系數(shù)；ρ為著陸場(chǎng)空氣密度；A為機(jī)翼參考面積；Fsc為主輪剎車所產(chǎn)生阻力；V為空速。地面風(fēng)會(huì)影響動(dòng)壓，設(shè)定Vw為風(fēng)速，則有：

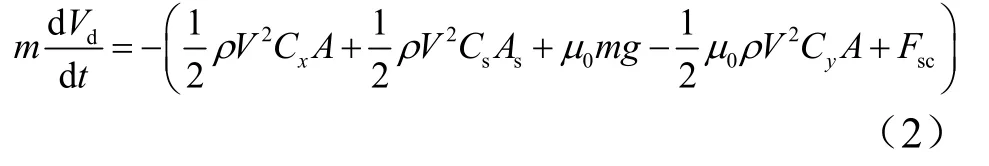
令：

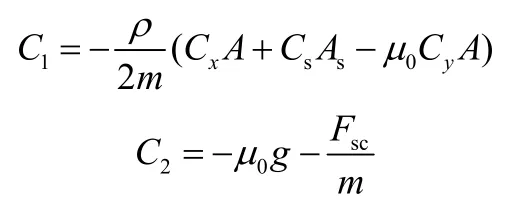
則式（2）可以寫成：

由于

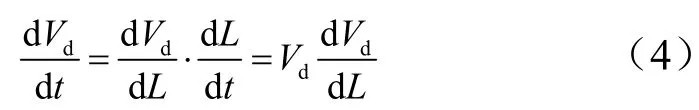
式中L為傘張滿后滑跑距離；順風(fēng)時(shí)Vd=V+Vw，逆風(fēng)時(shí)Vd=V-Vw，本文以順風(fēng)為例。

聯(lián)合式（3）得：

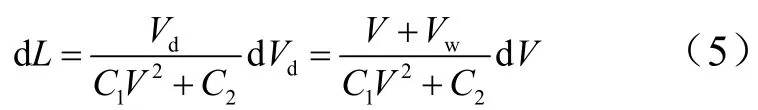
對(duì)式（5）積分后得：

傘開始張滿時(shí)速度為VM（空速），對(duì)應(yīng)滑跑距離L=0，因此可得：

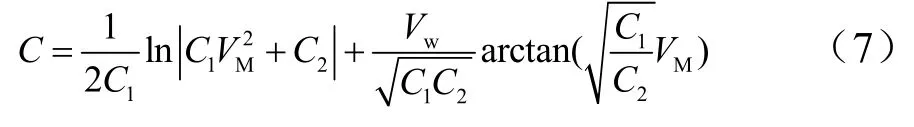
則得：

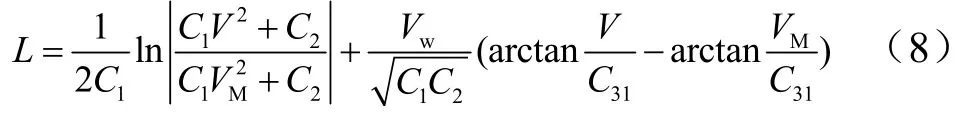
2 滑跑距離估算方法

2.1 正常滑跑工況

開傘到傘張滿時(shí)段，為簡(jiǎn)化分析，近似認(rèn)為飛行器勻速滑跑，滑跑距離為

式中tM為該時(shí)段時(shí)長(zhǎng)。

傘張滿到開始剎車時(shí)段，飛行器滑跑距離為

式中GV為剎車時(shí)刻的空速；。

開始剎車到拋傘時(shí)段，滑跑距離為

拋傘后滑跑過(guò)程中，當(dāng)飛行器速度達(dá)到順風(fēng)風(fēng)速時(shí)，空速為零，此后飛行器不受氣動(dòng)阻力、升力以及減速傘的作用力，水平方向只有摩擦力、剎車產(chǎn)生的阻力作用。

拋傘到飛行器達(dá)到風(fēng)速時(shí)段，滑跑距離為

從空速為零到停機(jī)時(shí)段：

從空速為零到停機(jī)的滑跑距離為

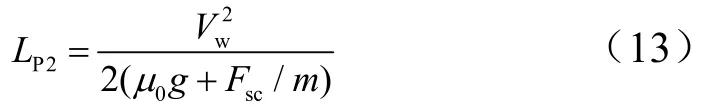
則從開傘到停機(jī)的滑跑距離為

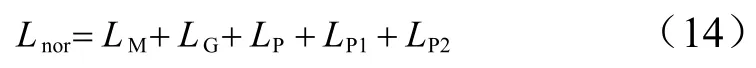
2.2 用傘無(wú)剎車工況

傘張滿到拋傘時(shí)段，飛行器滑跑距離為

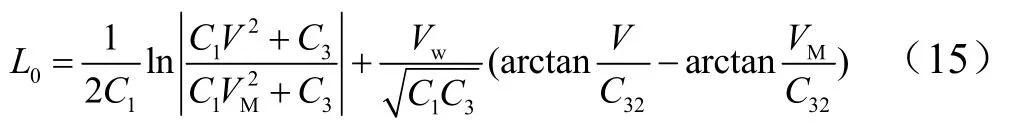
拋傘后滑跑過(guò)程中，當(dāng)飛行器速度達(dá)到風(fēng)速時(shí)，空速為零，此后飛行器不受氣動(dòng)阻力、升力以及減速傘的作用力，水平方向只有摩擦力作用。

拋傘到飛行器達(dá)到風(fēng)速時(shí)段，滑跑距離為

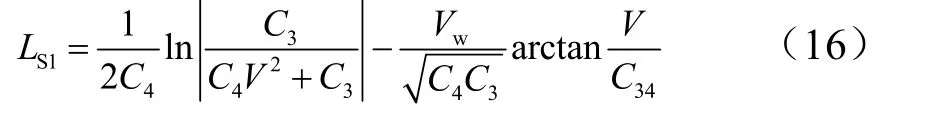
從空速為零到停機(jī)時(shí)段：

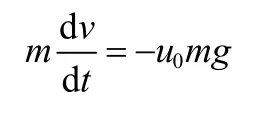
從空速為零到停機(jī)的滑跑距離為

則從開傘到停機(jī)的滑跑距離為

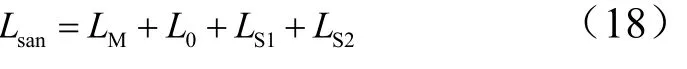
2.3 剎車不用傘工況

為簡(jiǎn)化分析，開傘到開傘失敗信息反饋過(guò)程，近似認(rèn)為飛行器勻速滑跑，滑跑距離為

式中tsb為開傘到開傘失敗信息反饋時(shí)間；V1為該時(shí)段的滑跑速度。

開傘失敗后開始剎車，當(dāng)飛行器速度達(dá)到風(fēng)速時(shí)，空速為零，此后飛行器不受氣動(dòng)阻力、升力作用，水平方向只有摩擦力、剎車產(chǎn)生的阻力作用。

開始剎車到飛行器達(dá)到風(fēng)速時(shí)段，滑跑距離為

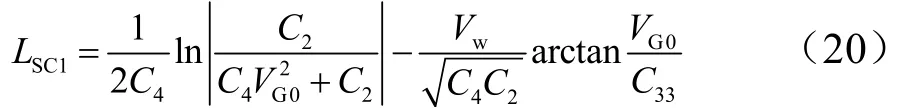
式中VG0為該工況下的開始剎車速度（空速），不同于正常滑跑時(shí)開始剎車速度。

從空速為零到停機(jī)時(shí)段：

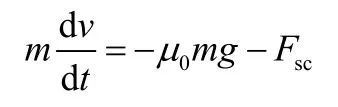
從空速為零到停機(jī)的滑跑距離為

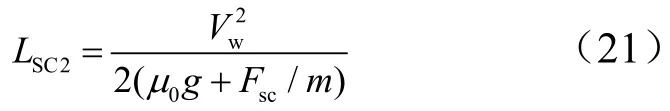
則從開傘（失敗）到停機(jī)的滑跑距離為

3 結(jié)束語(yǔ)

重復(fù)使用運(yùn)載器滑跑段無(wú)動(dòng)力，受氣動(dòng)力、風(fēng)、減速傘等一系列因素影響，運(yùn)動(dòng)規(guī)律較復(fù)雜。本文側(cè)重從工程應(yīng)用和初期總體設(shè)計(jì)的角度，提出一種簡(jiǎn)單易懂的滑跑距離估算方法，在跑道坐標(biāo)系下建立飛行器著陸滑跑估算模型，考慮減速傘和地面風(fēng)影響，研究不同滑跑工況下的滑跑距離估算方法。該估算方法簡(jiǎn)潔、算法易實(shí)現(xiàn)，適合工程應(yīng)用。