消防院校數學教學中“數學建模”融入研究

王慧穎 吳琦鳴 王兆強

摘要：現代消防科技的迅猛發展，為數學的實際運用提供了很好的平臺。消防院校數學課程教學也將必然適應這一趨勢。文章結合當前消防院校教學需貼近實戰，符合消防實戰的目標和需求，分析了當前消防院校數學教學發展現狀，簡要介紹了數學建模的概念及應用領域，結合實際給出了現代消防人才培養的目標，將數學建模知識融入到傳統的數學教學中，通過創新基本理論和教學方法，能夠培養出新時代全面發展的高素質消防指揮人才，更好的為消防應急現代化服務。

關鍵詞：數學建模;數學教育;教學研究

數學是消防院校消防工程、消防指揮、搶險救援指揮與技術等專業的通識必修課程，主要向學員教授高等數學、線性代數及概率論與數理統計等數學基礎知識以及傳遞數學思想，使學員通過學習數學掌握相應的計算方法，具備一定的邏輯思考能力，形成解決和分析消防相關問題的能力以及自主創新的能力，同時也是學習滅火、搶險救援等消防相關專業課程的基本工具。目前消防院校數學課程教學從目標、內容、方法以及考核方式等方面存在著一定的問題，這將導致數學學科的教學任務很難達到院校培養人才的目的和期望，也很難達到學員畢業滿足崗位技能的需求。習近平總書記在空軍航空大學視察時強調，要貫徹新時代黨的強軍思想，貫徹新時代軍事戰略方針，貫徹新時代軍事教育方針，深化改革創新，不斷提高辦學育人水平，努力開創學校建設發展新局面。始終堅持讓院校精準對接部隊，課堂緊密銜接戰場，加強軍魂教育，強化戰斗精神，切實以高素質人才方陣托舉新時代強軍偉業。在此背景下，文章將數學建模融入到消防院校數學教學中，實現理論聯系實際，教學貼近實戰，實現實戰能力的根本性要求，為一線培養出高素質的消防指揮人才。

1? 數學建模的概念

數學建模是對當前實際問題進行調查和研究，對研究對象的情況進行了解并給出相應的簡化假設，利用數學的語言和符號將實際問題量化出數學表達式，即數學模型，并利用定理、推論、圖解及優化算法等傳統和現代的數學求解方法對數學模型進行優化求解，并以此來解釋實際問題，在這個過程中，需要反復反饋問題解決情況從而驗證和完善數學模型，使其更貼近實際問題的需求，通過模型構建為解決實際問題提供了很好的科學依據和量化方法。也就是把實際問題進行提煉，并抽象出數學模型、求解模型、驗證模型，最后對實際問題給出科學解釋和決策依據。因此完整的數學模型構建步驟為問題調研、提出假設、模型建立、模型求解、模型驗證和模型應用。模型構建流程如圖1所示。

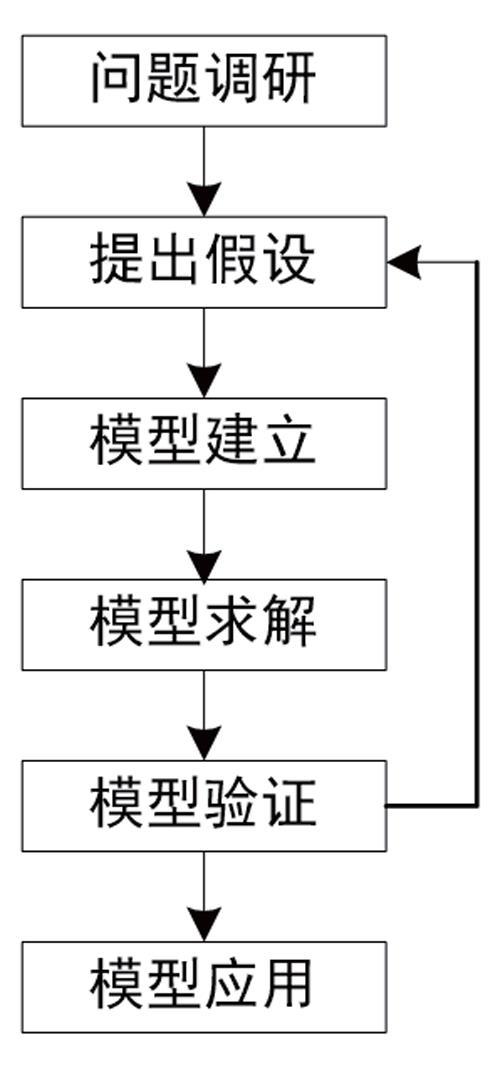
二十世紀六七十年代西方國家的一些大學引進了數學建模課程，而我國是從80年代初由清華大學和北京理工大學開始引進數學建模課程的學習。而數學建模競賽的開展是由美國在20世紀80年代開始舉辦的。之后幾年里，我國教育部也不斷推動和開展數學建模競賽，形成了每年一屆的高校大學生數學建模競賽的規模。競賽受到各高校師生的積極響應，參加學生逐年增加。數學建模競賽至今已有二十多年的發展，其影響力是有目共睹的，我國大多數院校都已積極開展數學建模課程和相關講座，該課程的學習可以增加學生學習數學的興趣，激發學生利用數學分析的方法解決實際問題的能力，為理論聯系實際教學提供了一條有效的途徑。

數學建模的應用非常廣泛，涉及數學、物理、化學、氣象、管理、經濟、醫學、工程、地質等不同學科不同領域。對數學建模理論知識的運用能夠有效解決生產和生活中存在的實際問題，能夠實現社會資源的優化與重整。隨著社會不斷發展，與人們息息相關的生存環境不斷的發生變化，目前我國災害頻繁發生，災害類型和分布具有多樣性，因此對消防員綜合素質的要求也越來越高。從消防領域而言，如何運用數學建模在防火、滅火以及救援方面做到科學分析、科學規劃、科學決策已慢慢成為一種必然趨勢。掌握數學建模的思想和技能也應成為消防院校學員學習的重點課程，從而實現課堂緊密銜接戰場，加強軍魂教育。

2? 消防院校數學教學現狀分析

2.1? 學校性質及特點

消防院校是國內一所專門面向社會和消防隊伍招生并為消防隊伍培養具有初級指揮員的本科院校，主要承擔國家綜合性消防救援隊伍初級指揮員培養、干部學歷教育、繼續教育、在職培訓、應急管理和消防救援科學技術研究、決策咨詢及相關交流合作工作，參加重大應急救援機動增援等任務。其專業和學科的設置與地方的高校存在著較大的區別，一方面因消防院校發展歷史等原因專業種類較少，目前有消防工程、消防指揮、搶險救援指揮與技術、飛行器控制與信息工程、思想政治教育、消防政治工作共六個專業;另一方面從課程設置上來看，文化基礎課程與地方高校沒有太大差異，但防火、滅火、救援等專業課程的設置在地方高校還沒有設置。學員從消防院校畢業后從事戰備執勤、消防監督、火災救援及事故調查等崗位職責，因此初級指揮員所具備的綜合素質，既要體現在具備全面的專業知識和道德素質，更要體現在過硬的體能素質、軍事素質、專業技能以及管理指揮水平等方面。因此，數學作為一門通識課程，考慮消防院校實際培養目標，就不能完全按照地方高校一樣，在數學教學上講解過多、過深的基礎理論知識，而是需要在基礎理論講解的基礎上更注重理論聯系實際的教學方法。

2.2? 學員特點及基本情況

消防隊伍學院的學員分為隊伍生和青年生，隊伍生選自全國各地方基層消防隊伍，青年生按照全國當年高考成績進行提前批次錄取。學員成分大致可分為初中文化、高中文化、大專文化以及本科文化多層次，其文化程度及教育背景差異性較大。從數學整體授課情況來看，學員普遍自身數學基礎較為薄弱，其中隊伍生在入學之前就職于基層消防隊伍，需要按要求完成執勤、戰備、出警以及體能訓練等繁重的任務，很少有學員將經歷用于文化課程的學習，對之前學過的數學知識及運用技能都已退化，入學后難以從工作狀態快速適應緊張連續的學習任務。對基礎較差的隊伍學員來說，大學數學學科的學習不僅聽不懂也不具備自學的能力。青年生經歷過高考的選拔，數學基礎普遍較強，同樣的授課內容青年生可以聽得懂并舉一反三，而且擅長提問并挑戰具有一定難度的數學題。無論是隊伍生還是青年生，他們對數學學習重要性的主觀認識不足，多數學員認為畢業后從事的消防相關崗位對數學知識的運用要求不高，因此學習興趣和自我要求都很低。

2.3? 數學教學基本情況

消防院校在數學課程教材方面以教學計劃、教學內容以及教學對象等方面進行篩選，整體難度較地方高校有所降低，與現代消防領域中存在的實際問題結合較少，其實用性與應用性不高，很難滿足學員畢業后崗位需求，還將學員帶入學習數學無用的誤區中。教師在授課中以既定教學內容為主，教學模式多采用線下授課、形式單一，授課內容以概念、求解方法、證明過程作為教學目標，通過練習和留作業的方式鞏固知識點，多數學員上課時無法聽懂、弄懂只能以灌輸方式學習并記住，這會導致學員在學習數學過程中感到單調、無味，采用短時間記憶的方式應對期中期末考試。至于將掌握的數學知識如何解決實際問題，卻是在教學過程中沒有體現出來，違背了消防院校培養人才的教學目標，極大影響到教學效果的實現。

3? 數學建模融入數學教學中的意義

3.1? 實現現代消防科學與數學方法的有機融合，教學目標面向消防實戰

隨著人類文明的發展，現代消防科學與數學科學密不可分。著名思想家馬克思曾經說過：“一門學科的發展，只有當它成功地運用數學時，才能達到真正完善的地步。”目前現代消防領域中存在的實際問題，往往需要收集各項數據，并根據實際問題建立出數學模型才可以在特定的約束條件下（如救援成本、救援時間等），準確、高效地執行防火監督、搶險救援以及火場滅火等工作。例如，地區災洪救援中專業救援人員派遣與救援最大效益之間的優化問題、城市區域消防設站布局問題、現場火災人員疏散問題、森林火災救援優化路徑問題等，都需要結合數學建模知識來建立數學模型，找出科學、合理的救援途徑。

教學中選擇與消防相關的實戰案例，并將數學建模思想融入到消防學院學員的數學教學中，能夠有效的實現消防科學與數學方法的有機融合，不僅能夠滿足實戰化教學育人的要求，還能夠讓學員真正了解學習數學的主要目的進而有針對性的學有所用、學以致用。

3.2? 構建學員學科知識體系，引導學員運用所學知識解決消防中實際問題

數學模型的構建不同于解決普通應用問題，模型構建涵蓋的知識面廣、綜合性強，涉及數學相關科目的知識點較多，同時也涉及到物理學科、化學學科等基礎科目以及防火、救援等消防相關科目的知識點。雖然模型構建相關知識點較多、問題呈現較為復雜，給學員解決實際問題帶來很大阻礙，但從模型構建步驟中問題調研、提出假設以及模型建立方面，在教師的正確引導下，一是可以使學員了解所學知識之間的聯系，通過反復運用、調研和選擇可以幫助學員鞏固和加深對各個知識點的理解和掌握程度;二是可以提升各科目中所含知識點的綜合運用，輔助學員將所學知識點及其聯系理清脈絡，達到形成較為完整的知識體系結構。因此將數學建模融入消防隊伍學院數學教學中具有重大實踐意義。再者，在模型求解、模型驗證以及模型應用中，學員可以真正領悟到所學知識的應用價值，也可以培養學員運用所學知識解決消防領域問題的能力。

3.3? 使學員掌握數學建模思想的同時提升學員對數學學習的興趣

目前消防院校數學教學在教學內容和教學方法上都無法避免以數學講數學，從定義、定理、推論再到例題講解等教學過程很難抓住學員長時間的關注力，學員在學習數學的授課過程中常常存在困頓、聽不懂、無趣等負面情緒，導致學員失去學習數學的興趣。這種情況的產生主要是因為所學知識完全脫離具體應用背景，學習目的不明確，只是為了應付考試而學習。如果教師能在授課過程中加入實際生活中的典型案例，尤其是與其相關的消防領域案例，能夠有效提升學員學習數學的興趣，幫助學員對數學知識的理解，同時可以培養學員思考、分析問題的能力，使學員從被動學習向主動學習轉變。再者，教師課堂授課內容的轉變，也給每位學員思考的機會，教師的角色也從講授者轉變為討論者、傾聽者，使課堂氛圍更加輕松、有趣。

3.4? 激發學員主動探究問題、自發學習的動力

數學建模課程目前學員還從未系統的學習，盡管有部分學員通過自學學習了一些內容，但是其掌握的程度還不夠深入和全面。因此，模型建立之前引導學員做足相關資料的調研，找到問題產生的關鍵，鍛煉學員通過推斷、驗證等研究手段，找出求解問題的方法。模型構建和模型求解中運用到的數學理論，需要學員不斷圍繞問題進行探索和自學，從而獲得新的數學理論知識。這也充分體現了從未知到已知的探索和學習的過程，能夠極大激發學員探究問題、自發學習的動力，培養學員解決問題的能力。

3.5? 培養學員的創新意識和能力

數學建模因背景不同沒有固定的表達模式、構建方法和求解算法，求解結果也沒有統一標準。然而在研究問題量化的過程中，需要學員突破以往思維定勢，根據實際問題以多角度出發，反復進行推理、分析、檢驗來構建模型，通過不斷的否定與再否定原則來完善模型。數學建模思想的引入可以有效培養學員的創新意識和能力。

總之，消防院校數學教學的實施必須滿足當前形勢下我國消防人才培養目標和需求，數學建模可以有效的將現代消防科學理論與實際問題聯系起來，其融入數學教學中具有深遠的意義。這是數學教育發展的必然趨勢，也是數學教育者要努力的根本目標。

參考文獻：

[1]陳富媛.高等數學教學中融入數學建模思想初探[J].現代職業教育，2018（04）：38-39.

[2]巴娜.在工科高等數學教學中融入數學建模思想的淺探[J].數學學習與研究，2017（11）：15.

[3]吳暉琴，潘小霞.軍事院校數學建模競賽輔導對策探討[J].長江大學學報（自科版），2014，11（34）：116-117+120+5.

[4]劉春艷.如何在高等數學教學中培養學生的創造性思維[J].科學咨詢（科技·管理），2019（12）：242.

[5]趙彥勇，葉緒國.數學建模思想融入課堂教學的策略和路徑研究[J].凱里學院學報，2021，39（03）：99-104.

[6]楊人子，王靜.數學建模思想融入高等數學的教學研究[J].大學教育，2021（03）：103-106.

[7]孟新友.數學建模思想融入新工科數學教學的探索[J].數學學習與研究，2020（24）：10-11.

[8]吳亞平，馮麗珠.淺析如何將數學建模思想有效融入線性代數課程教學[J].知識文庫，2020（19）：110+112.

[9]張軍，張新宇，劉菊紅，吳國棟，吳國榮.數學建模思想融入線性代數課程的教學模式[J].高師理科學刊，2020，40（10）：64-67+81.

[10]曹建美，王鳳翔.概率論與數理統計課程教學中融入數學建模思想的策略[J].西部素質教育，2020，6（12）：166-167.

[11]李娜.如何將數學建模思想融入到化學教學中[J].文理導航（中旬），2020（09）：84+86.

[12]司玉琴.將數學建模與科學計算思想融入高職院校數學教學的研究——以包頭鐵道職業技術學院為例[J].現代職業教育，2020（05）：176-177.

[13]劉敬剛，郭燕.融入數學建模思想的線性代數案例教學研究[J].赤峰學院學報（自然科學版），2020，36（01）：15-17.

[14]王曉斌，代麗娟.解析數學建模思想融入應用型本科高校數學教學的途徑[J].現代職業教育，2020（01）：166-167.

[15]湯秀良.基于建模思想的中等職業學校數學教學探究[J].技術與市場，2017，24（04）：275+277.

Research on integrating "mathematical modeling"

into mathematics teaching in fire fighting colleges

Wang Huiying1，Wu Qiming1，Wang Zhaoqiang2

（1.China Fire and Rescue Institute;2.Rocket Force Engineering University ）

Abstract：The rapid development of modern fire science and technology provides a good platform for the practical application of mathematics.The teaching of mathematics in fire fighting colleges and universities will inevitably adapt to this trend.Combining with the current fire colleges teaching should be close to actual combat， in line with the fire field goals and requirements， analyzes the current situation of the development of the current fire education， this paper briefly introduces the mathematical modeling and application field， the concept of modern fire control are given with practical talents training target， the mathematical modeling knowledge into the traditional mathematical teaching， the basic theory and method of teaching through innovation，Can train a new era of comprehensive development of high-quality fire command personnel， better for the modernization of fire emergency services.

Keywords：mathematical modeling; mathematics education; teaching